G Chaudhuri
IIPM Kolkata, AQ-6, Sector V, Salt Lake City, Kolkata, 700 091, India
Correspondence to: G Chaudhuri , IIPM Kolkata, AQ-6, Sector V, Salt Lake City, Kolkata, 700 091, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Analysts are often interested in obtaining component reliabilities by analyzing system life data. Making a series system assumption and applying a competing risk model generally does this. In practice, the data consists of a system life-length and a subset of components that contains the true cause of system failure (the true cause of system failure is masked from our knowledge). We consider a series system composed of independent Weibull components with common shape parameter and different scale parameters. It is shown that the IFRA-ness of the system is measured by the common shape parameter, which is also known as the aging factor. We derive the consistency and asymptotic normality of the MLEs of the scale parameters under random masking.
Keywords:
Masked Data, Competing Risk, Weibull Distribution, Maximum Likelihood Estimates, Aging, Schur-Concavity
Cite this paper: G Chaudhuri , On Competing Risk Model Under Random Masking, American Journal of Mathematics and Statistics, Vol. 3 No. 1, 2013, pp. 17-20. doi: 10.5923/j.ajms.20130301.02.
1. Introduction
In industrial problems, we are often interested in estimating component reliabilities from system lifetime data. In this context, the competing risk model is normally used. That is, component reliability from system life-data is generally estimated by assuming a series system and applying a competing risk model, where the system life-data and also the cause of system failure are known. The combined data can then be employed to estimate life distribution of the system and each of its components. In practice, however, this type of analysis is confounded with a problem of masking (the exact cause of failure is unknown). It is mentioned in[4] that “… investigation of cause of failure is expensive and time consuming, and hence sometimes the cause of failure is not observed, even if the failure time is recorded”. When a large computer system fails in the field, analysis is usually performed (see[7]) such that a small subset of components, perhaps a circuit card, is identified as the cause of failure. In an attempt to repair the system as quickly as possible, the entire subset of components is replaced and exact failing component may be investigated further. We call the data, for which cause of failure is narrowed to a subset of components, masked because the true cause of failure is masked from our knowledge. The resulting quantities obtained are then the system-life and the partial information on the cause of failure.[4] considered a model involving a series system of two components in which n systems are put on test and only for m (<n) systems, the failure times and the cause of failure were noted while the remaining n-m observations include only the failure times (i.e., n-m is the number of masked data). The model in[4] was extended by[7] and[2] to a model where they allowed an arbitrary number of components in series and random masking. They assumed the lifetime of the i-th component to be exponential with unknown but constant parameter 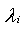 . They obtained the closed form expression for the MLEs of the parameters when the system has two components. For the case of three component system, they used the Picard’s method to obtain approximate solution to the MLE of
. They obtained the closed form expression for the MLEs of the parameters when the system has two components. For the case of three component system, they used the Picard’s method to obtain approximate solution to the MLE of 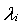 , i=1,2,3. In[3], the general multi-component system is discussed and they proved consistency of the MLEs under certain conditions.No study has been reported so far for the above model taking the aging of the component into consideration. Aging is an important aspect in reliability to deal with. We consider a series system consisting of two components having Weibull
, i=1,2,3. In[3], the general multi-component system is discussed and they proved consistency of the MLEs under certain conditions.No study has been reported so far for the above model taking the aging of the component into consideration. Aging is an important aspect in reliability to deal with. We consider a series system consisting of two components having Weibull 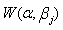 with distribution function
with distribution function 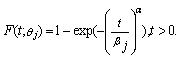 where
where 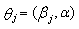 . Let
. Let 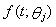 denote the density of
denote the density of 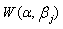 .The paper is organized as follows. In Section 2, we show that the IFRA (increasing failure rate average)-ness of the series system consisting of Weibul components with common shape parameter
.The paper is organized as follows. In Section 2, we show that the IFRA (increasing failure rate average)-ness of the series system consisting of Weibul components with common shape parameter 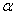 is measured by
is measured by 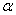 . In Section 3, we develop the likelihood function for a n-component series system. In Section 4, we establish the consistency and asymptotic normality of the estimates of the scale parameters
. In Section 3, we develop the likelihood function for a n-component series system. In Section 4, we establish the consistency and asymptotic normality of the estimates of the scale parameters 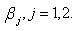
2. Notion of Aging
The following definition is due to[1].Definition 2.1: A system with exchangeable units {1,2…,n} age or wear out with respect to age, if their joint survival function 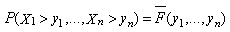 is Schur concave.Theorem 2.1 (see[1]): Let
is Schur concave.Theorem 2.1 (see[1]): Let 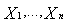 be the independent lifetimes of n units, each with specified univariate distribution F. Suppose further that
be the independent lifetimes of n units, each with specified univariate distribution F. Suppose further that 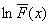 is concave when finite. Then
is concave when finite. Then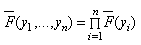 is Schur-concave.Consider a series system composed of n independent Weibull components with common shape parameter
is Schur-concave.Consider a series system composed of n independent Weibull components with common shape parameter 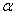 . Then it is easy to see, in the light of the above theorem, that (ⅰ) the system age positively if
. Then it is easy to see, in the light of the above theorem, that (ⅰ) the system age positively if 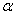 >1,(ⅱ) the system age negatively if
>1,(ⅱ) the system age negatively if 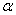 <1, and,(ⅲ) the system has no age if
<1, and,(ⅲ) the system has no age if 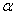 =1.Hence
=1.Hence 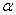 is the aging factor for the system.We shall now prove that the IFRA-ness of a component/system is measured by
is the aging factor for the system.We shall now prove that the IFRA-ness of a component/system is measured by 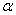 . To this end, we give the following definition.Definition 2.2 (see[6]): Let F and G be continuous life distributions. We say, F is more IFRA than G if
. To this end, we give the following definition.Definition 2.2 (see[6]): Let F and G be continuous life distributions. We say, F is more IFRA than G if 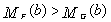 for all 0is defined by
for all 0is defined by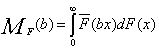 | (2.1) |
Theorem 2.2: Consider two series systems 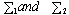 . Let
. Let  be composed of n independent Weibull components with common shape parameter
be composed of n independent Weibull components with common shape parameter 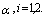 Then
Then 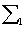 is more IFRA than
is more IFRA than 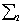 if and only if
if and only if 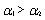 .Proof: Let
.Proof: Let 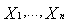 be the independent lifetimes of n components of the series system. Let
be the independent lifetimes of n components of the series system. Let 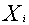 follow Weibull
follow Weibull 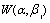 , j=1,…,n. Now if
, j=1,…,n. Now if 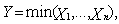 then
then 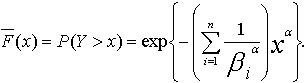 | (2.2) |
Now, form (2.1), we have 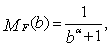 | (2.3) |
which is an increasing function of , for 03. The likelihood Function
Consider n series systems each having J components. The random life-lengths of the j-th component in the i-th system, i=1,…,n and j=1,…,J, is denoted by  . Let
. Let  denote the life-length of the i-th system so that
denote the life-length of the i-th system so that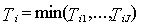 | (3.1) |
for i=1,…,n. We assume that 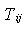 ’s are independent. The random variables
’s are independent. The random variables 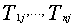 constitute a random sample from a common absolutely continuous distribution
constitute a random sample from a common absolutely continuous distribution 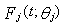 with probability density
with probability density 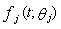 . Let
. Let 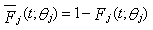 denote the reliability (survival) function of the j-th component at time t. After the failure of the i-th system at time
denote the reliability (survival) function of the j-th component at time t. After the failure of the i-th system at time 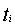 , an analysis of the possible cause of failure may be carried out and as a result, a non-empty set, say
, an analysis of the possible cause of failure may be carried out and as a result, a non-empty set, say 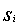 , is identified which is known to contain the true cause of failure. Before the analysis,
, is identified which is known to contain the true cause of failure. Before the analysis, 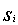 is unknown and considered random. Such a random set is denoted by
is unknown and considered random. Such a random set is denoted by 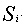 Let
Let 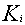 be the random index of the components causing the failure of the i-th system. (
be the random index of the components causing the failure of the i-th system. (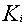 is assumed to be unique). Only when
is assumed to be unique). Only when 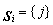 , we will know that
, we will know that 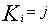 , in any other case, we can only state that
, in any other case, we can only state that 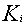
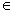
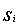 (i.e., the true cause of failure is masked from our knowledge).The observations
(i.e., the true cause of failure is masked from our knowledge).The observations 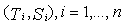 are assumed to be independent and the observed data is expressed as
are assumed to be independent and the observed data is expressed as 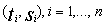 .The maximum likelihood estimate can now be obtained by maximizing the following expression (see[3]):
.The maximum likelihood estimate can now be obtained by maximizing the following expression (see[3]):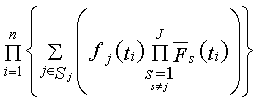 | (3.2) |
4. Consistency and Asymptotic Normality
The likelihood (3.2) seems to be intractable analytically when 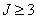 . Therefore, we consider a series system with two independent
. Therefore, we consider a series system with two independent 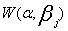 , j=1,2, components. Suppose
, j=1,2, components. Suppose 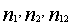 are the number of observations
are the number of observations 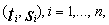 such that
such that 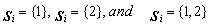 respectively. From (3.2) one can obtain the log-likelihood function
respectively. From (3.2) one can obtain the log-likelihood function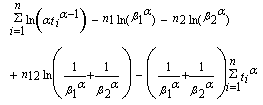 | (4.1) |
The MLEs are easily shown to be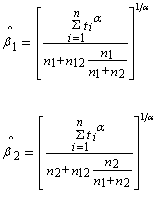 | (4.2) |
It is known that 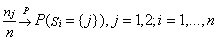 | (4.3) |
(see[5], p.356).We have for j=1,2,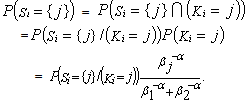 | (4.4) |
Thus, 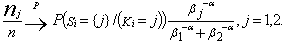 | (4.5) |
By WLLN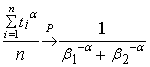 | (4.6) |
Therefore,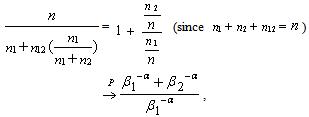 | (4.7) |
which follows under the assumption (see[3]) that 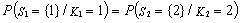 | (4.8) |
Hence, by the Slutskey’s Lemma, 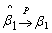 Similarly, one can show
Similarly, one can show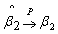 .Thus,
.Thus, 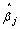 is a consistent estimate of
is a consistent estimate of 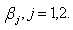 Now we shall establish the asymptotic normality of
Now we shall establish the asymptotic normality of 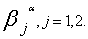 By the Lindeberg-Levy Central Limit Theorem, we have
By the Lindeberg-Levy Central Limit Theorem, we have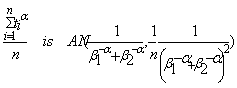 Hence, from (4.7) and the Slutskey’s lemma, we have
Hence, from (4.7) and the Slutskey’s lemma, we have 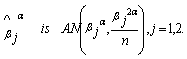
5. Conclusions
So far the masked data have been studied for the system composed of exponential components. Though there are some papers (see[8], for example) addressing Weibull distribution, no attention is paid to the aging aspect of the situation. In this paper, we have considered a simple series system composed of two Weibull components having the common shape parameter. We have taken the shape parameters to be the same, because (as shown in this paper) it is the aging factor of interest and it characterizes the IFRA-ness of a system. So, by taking the shape parameters to be common, we are basically assuming that the system is consisting of components with the same amount of IFRA-ness.
References
| [1] | Barlow R E and M B Mendel (1993). Similarity as a probabilistic characteristic of aging, Reliability and Decision making, ed., R E Barlow and C A Claoroti and F Spizzichino, Chapman and Hall, London. |
| [2] | Gastaldi T (1994). Improved maximum likelihood estimation for component reliabilities with Miyakawa-Usher-Hodgson - Guess estimator under censored search for the cause of failure, Statistics and Probability Letters, 19, 5-18. |
| [3] | Guess M F ,J S Usher and T J Hodgson (1991). Estimating system and component reliabilities under partial information on cause of failure, J Statistical Planning and Inference, 29, 75-85. |
| [4] | Miyakawa M (1984). Analysis of incomplete data in competing risk model, IEEE Transactions on reliability, 33, 293-296. |
| [5] | Rao C R (1973). Linear Statistical inference and its application, Wiley eastern Pvt Ltd, New Delhi. |
| [6] | Tiwari R C and Joyti N Zalkikar (1988). Testing whether F is more IFRA than G, Microelectronics and Reliability, 28, 703-712. |
| [7] | Usher J S and T J Hodgson (1988). Maximum likelihood analysis of component reliability using masked system life data, IEEE Transactions on Reliability, 37, 550-555. |
| [8] | Usher J S (1996). Weibull component reliability prediction in the presence of masked data, IEEE Transaction on Reliability, 45, 229-232. |

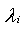 . They obtained the closed form expression for the MLEs of the parameters when the system has two components. For the case of three component system, they used the Picard’s method to obtain approximate solution to the MLE of
. They obtained the closed form expression for the MLEs of the parameters when the system has two components. For the case of three component system, they used the Picard’s method to obtain approximate solution to the MLE of 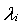 , i=1,2,3. In[3], the general multi-component system is discussed and they proved consistency of the MLEs under certain conditions.No study has been reported so far for the above model taking the aging of the component into consideration. Aging is an important aspect in reliability to deal with. We consider a series system consisting of two components having Weibull
, i=1,2,3. In[3], the general multi-component system is discussed and they proved consistency of the MLEs under certain conditions.No study has been reported so far for the above model taking the aging of the component into consideration. Aging is an important aspect in reliability to deal with. We consider a series system consisting of two components having Weibull 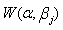 with distribution function
with distribution function 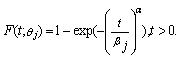 where
where 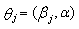 . Let
. Let 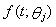 denote the density of
denote the density of 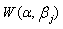 .The paper is organized as follows. In Section 2, we show that the IFRA (increasing failure rate average)-ness of the series system consisting of Weibul components with common shape parameter
.The paper is organized as follows. In Section 2, we show that the IFRA (increasing failure rate average)-ness of the series system consisting of Weibul components with common shape parameter 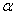 is measured by
is measured by 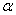 . In Section 3, we develop the likelihood function for a n-component series system. In Section 4, we establish the consistency and asymptotic normality of the estimates of the scale parameters
. In Section 3, we develop the likelihood function for a n-component series system. In Section 4, we establish the consistency and asymptotic normality of the estimates of the scale parameters 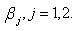
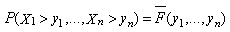 is Schur concave.Theorem 2.1 (see[1]): Let
is Schur concave.Theorem 2.1 (see[1]): Let 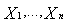 be the independent lifetimes of n units, each with specified univariate distribution F. Suppose further that
be the independent lifetimes of n units, each with specified univariate distribution F. Suppose further that 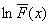 is concave when finite. Then
is concave when finite. Then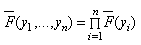 is Schur-concave.Consider a series system composed of n independent Weibull components with common shape parameter
is Schur-concave.Consider a series system composed of n independent Weibull components with common shape parameter 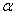 . Then it is easy to see, in the light of the above theorem, that (ⅰ) the system age positively if
. Then it is easy to see, in the light of the above theorem, that (ⅰ) the system age positively if 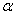 >1,(ⅱ) the system age negatively if
>1,(ⅱ) the system age negatively if 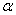 <1, and,(ⅲ) the system has no age if
<1, and,(ⅲ) the system has no age if 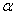 =1.Hence
=1.Hence 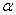 is the aging factor for the system.We shall now prove that the IFRA-ness of a component/system is measured by
is the aging factor for the system.We shall now prove that the IFRA-ness of a component/system is measured by 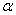 . To this end, we give the following definition.Definition 2.2 (see[6]): Let F and G be continuous life distributions. We say, F is more IFRA than G if
. To this end, we give the following definition.Definition 2.2 (see[6]): Let F and G be continuous life distributions. We say, F is more IFRA than G if 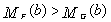 for all 0
for all 0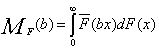
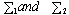 . Let
. Let 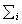 be composed of n independent Weibull components with common shape parameter
be composed of n independent Weibull components with common shape parameter 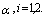 Then
Then 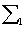 is more IFRA than
is more IFRA than 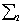 if and only if
if and only if 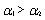 .Proof: Let
.Proof: Let 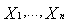 be the independent lifetimes of n components of the series system. Let
be the independent lifetimes of n components of the series system. Let 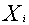 follow Weibull
follow Weibull 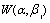 , j=1,…,n. Now if
, j=1,…,n. Now if 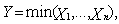 then
then 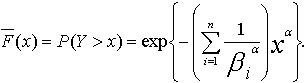
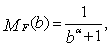
 . Let
. Let  denote the life-length of the i-th system so that
denote the life-length of the i-th system so that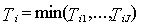
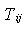 ’s are independent. The random variables
’s are independent. The random variables 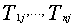 constitute a random sample from a common absolutely continuous distribution
constitute a random sample from a common absolutely continuous distribution 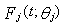 with probability density
with probability density 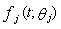 . Let
. Let 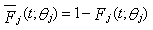 denote the reliability (survival) function of the j-th component at time t. After the failure of the i-th system at time
denote the reliability (survival) function of the j-th component at time t. After the failure of the i-th system at time 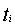 , an analysis of the possible cause of failure may be carried out and as a result, a non-empty set, say
, an analysis of the possible cause of failure may be carried out and as a result, a non-empty set, say 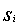 , is identified which is known to contain the true cause of failure. Before the analysis,
, is identified which is known to contain the true cause of failure. Before the analysis, 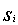 is unknown and considered random. Such a random set is denoted by
is unknown and considered random. Such a random set is denoted by 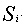 Let
Let 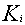 be the random index of the components causing the failure of the i-th system. (
be the random index of the components causing the failure of the i-th system. (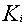 is assumed to be unique). Only when
is assumed to be unique). Only when 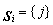 , we will know that
, we will know that 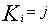 , in any other case, we can only state that
, in any other case, we can only state that 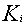
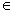
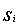 (i.e., the true cause of failure is masked from our knowledge).The observations
(i.e., the true cause of failure is masked from our knowledge).The observations 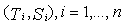 are assumed to be independent and the observed data is expressed as
are assumed to be independent and the observed data is expressed as 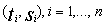 .The maximum likelihood estimate can now be obtained by maximizing the following expression (see[3]):
.The maximum likelihood estimate can now be obtained by maximizing the following expression (see[3]):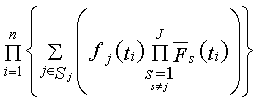
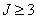 . Therefore, we consider a series system with two independent
. Therefore, we consider a series system with two independent 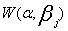 , j=1,2, components. Suppose
, j=1,2, components. Suppose 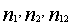 are the number of observations
are the number of observations 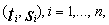 such that
such that 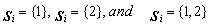 respectively. From (3.2) one can obtain the log-likelihood function
respectively. From (3.2) one can obtain the log-likelihood function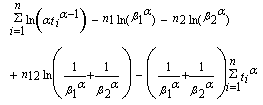
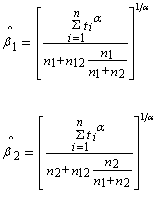
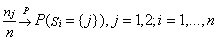
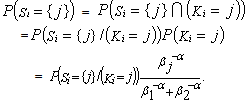
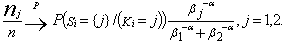
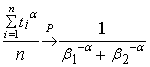
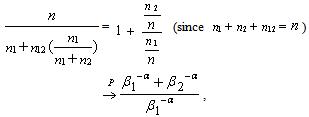
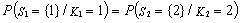
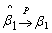 Similarly, one can show
Similarly, one can show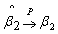 .Thus,
.Thus, 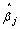 is a consistent estimate of
is a consistent estimate of  Now we shall establish the asymptotic normality of
Now we shall establish the asymptotic normality of  By the Lindeberg-Levy Central Limit Theorem, we have
By the Lindeberg-Levy Central Limit Theorem, we have Hence, from (4.7) and the Slutskey’s lemma, we have
Hence, from (4.7) and the Slutskey’s lemma, we have 
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML