-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2012; 2(6): 221-225
doi: 10.5923/j.ajms.20120206.10
On Applications of Fractional Calculus Involving Summations of Series
Praveen Agarwal
Department of Mathematic Anand International College of Engineering Jaipur, 302012, India
Correspondence to: Praveen Agarwal , Department of Mathematic Anand International College of Engineering Jaipur, 302012, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A significantly large number of earlier works on the subject of fractional calculus give interesting account of the theory and applications of fractional calculus operators in many different areas of mathematical analysis (such as ordinary and partial differential equations, integral equations, special functions, summation of series, et cetera). The main object of the present paper is to obtain number of summations of series concerning generalized hypergeometric functions. Our finding provides interesting unifications and extensions of a number of new and known results.
Keywords: Fractional Calculus; Special Function, Summation of Series, Generalized Leibniz Rule, Generalized Hypergeometric Series, Laguerre Polynomials
Cite this paper: Praveen Agarwal , "On Applications of Fractional Calculus Involving Summations of Series", American Journal of Mathematics and Statistics, Vol. 2 No. 6, 2012, pp. 221-225. doi: 10.5923/j.ajms.20120206.10.
1. Introduction
- One of the most frequently encountered tools in the theory of fractional calculus (that is, differentiation and integration of an arbitrary real or complex order) is furnished by the familiar differintegral operator
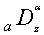 defined and represented by Oldham and Spanier[12]:
defined and represented by Oldham and Spanier[12]: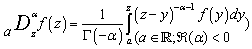 | (1.1) |
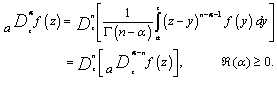 | (1.2) |
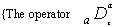 provides a generalization of the familiar differential and integral operator, viz.,
provides a generalization of the familiar differential and integral operator, viz., 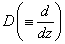 and
and 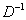 }.For a=0 the operator
}.For a=0 the operator 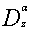 is given by
is given by 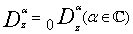 | (1.3) |
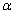 (or –
(or –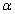 ). Moreover, when
). Moreover, when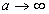 , Equation (1.1) may be identified with the definition of the familiar Weyl fractional derivative (or integral) of order
, Equation (1.1) may be identified with the definition of the familiar Weyl fractional derivative (or integral) of order 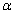 (or –
(or –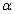 ).In recent years there has appeared a great deal of literature discussing the application of the aforementioned fractional calculus operators in a number of areas of mathematical analysis (such as ordinary and partial differential equations, integral equations, summation of series, et cetera) and now stands on fairly firm footing through the research contribution of various authors (cf., e.g.,[2],[5-7],[9-14],[16] and[17]). In the present paper main object is to obtain number of summations of series concerning generalized hypergeometric functions. The familiar Leibniz rule for ordinary derivatives admits itself of the following extension in terms of the Riemann-Liouville operator
).In recent years there has appeared a great deal of literature discussing the application of the aforementioned fractional calculus operators in a number of areas of mathematical analysis (such as ordinary and partial differential equations, integral equations, summation of series, et cetera) and now stands on fairly firm footing through the research contribution of various authors (cf., e.g.,[2],[5-7],[9-14],[16] and[17]). In the present paper main object is to obtain number of summations of series concerning generalized hypergeometric functions. The familiar Leibniz rule for ordinary derivatives admits itself of the following extension in terms of the Riemann-Liouville operator 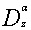 defined by (1.3):
defined by (1.3):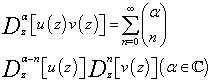 | (1.4) |
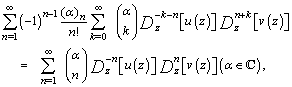 | (1.5) |
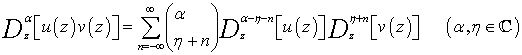 | (1.6) |
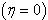 ,yields the Leibniz rule (1.4).The condition of validity of the above results is given by T. J. Osler[13, p. 664-665]). The generalized hypergeometric function of one variable viz.,
,yields the Leibniz rule (1.4).The condition of validity of the above results is given by T. J. Osler[13, p. 664-665]). The generalized hypergeometric function of one variable viz., 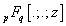 defined and represented as follows (see e.g.[15, p.19]) is also required here:
defined and represented as follows (see e.g.[15, p.19]) is also required here: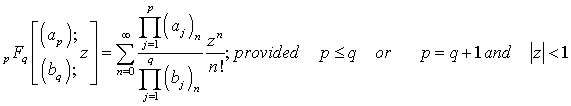 | (1.7) |
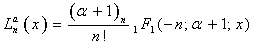 | (1.8) |
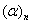 is the Pochhammer symbol and
is the Pochhammer symbol and 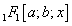 is a confluent hypergeometric function of the first kind (see e.g.[8]).
is a confluent hypergeometric function of the first kind (see e.g.[8]).2. Main results
- In this section, we shall establish some new summation formulae for the generalized hypergeometric function
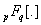 .Summation Formulae 2.1
.Summation Formulae 2.1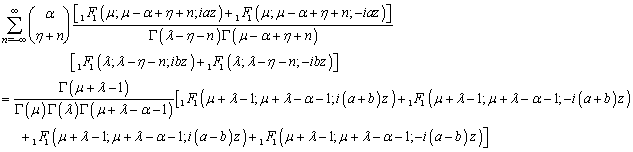 | (2.1) |
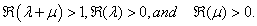 The conditions of validity of the above results follow easily from the conditions given by T. J. Osler[13, p. 664-665]). Summation Formulae 2.2
The conditions of validity of the above results follow easily from the conditions given by T. J. Osler[13, p. 664-665]). Summation Formulae 2.2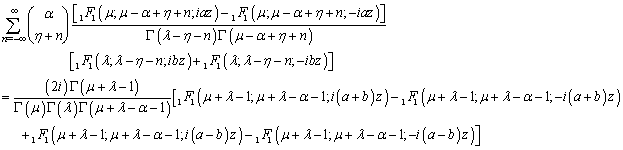 | (2.2) |
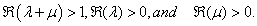 The conditions of validity of the above results follow easily from the conditions given by T. J. Osler[13, p. 664-665]). Summation Formulae 2.3
The conditions of validity of the above results follow easily from the conditions given by T. J. Osler[13, p. 664-665]). Summation Formulae 2.3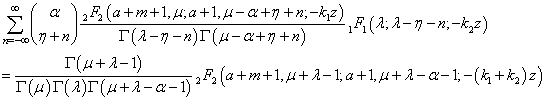 | (2.3) |
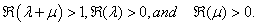 The conditions of validity of the above results follow easily from the conditions given by T. J. Osler[13, p. 664-665]). Summation Formulae 2.4
The conditions of validity of the above results follow easily from the conditions given by T. J. Osler[13, p. 664-665]). Summation Formulae 2.4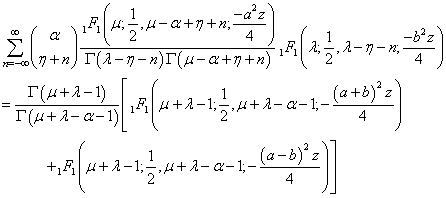 | (2.4) |
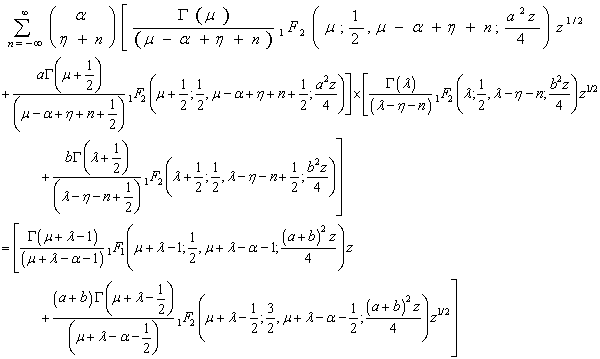 | (2.5) |
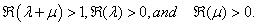 The conditions of validity of the above results follow easily from the conditions given by T. J. Osler[ 13, p. 664-665]).Proofs:The results are obtained by assigning particular values to the functions u (z) and v (z) in the generalized Leibniz rule (1.6). If we put
The conditions of validity of the above results follow easily from the conditions given by T. J. Osler[ 13, p. 664-665]).Proofs:The results are obtained by assigning particular values to the functions u (z) and v (z) in the generalized Leibniz rule (1.6). If we put 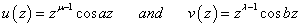 in (1.6), then L.H.S. of (1.6) becomes
in (1.6), then L.H.S. of (1.6) becomes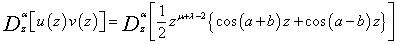 and using known result[4, p.189, eqn. (32)], we get
and using known result[4, p.189, eqn. (32)], we get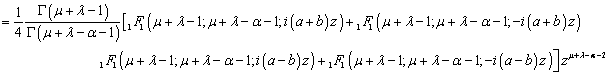 | (2.6) |
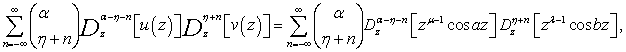 | (2.7) |
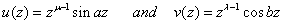 in (1.6), proceed on similar lines as adopted in (2.1) and using known results[4, p.188, Eq. (21)], we obtained the required interesting formulae (2.2).Next, If we take
in (1.6), proceed on similar lines as adopted in (2.1) and using known results[4, p.188, Eq. (21)], we obtained the required interesting formulae (2.2).Next, If we take 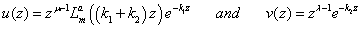 in (1.6), proceed on similar lines as adopted in (2.1) and using known results[4, p.193, Eq. (51) and p.187, Eq. (14)], we arrive at the required interesting formulae (2.3).Further, on putting
in (1.6), proceed on similar lines as adopted in (2.1) and using known results[4, p.193, Eq. (51) and p.187, Eq. (14)], we arrive at the required interesting formulae (2.3).Further, on putting 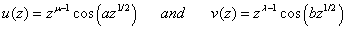 in (1.6), we easily obtained the formulae (2.4) after a little simplification on making use of similar lines of proof as adopted in (2.1) and using known results[4, p.190, Eq. (35)]:Similarly, if we take
in (1.6), we easily obtained the formulae (2.4) after a little simplification on making use of similar lines of proof as adopted in (2.1) and using known results[4, p.190, Eq. (35)]:Similarly, if we take 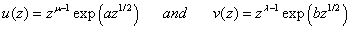 in (1.6), we easily arrive at the required formulae (2.5) after a little simplification on making use of similar lines of proof as adopted in (2.1) and using known results[4, p.190, Eq. (35)]
in (1.6), we easily arrive at the required formulae (2.5) after a little simplification on making use of similar lines of proof as adopted in (2.1) and using known results[4, p.190, Eq. (35)]3. Special Cases
- In view of the large number of parameters involved in the summations of series established above, these summations of series are capable of yielding a number of known and new results. We record here only one special case for lack of space. For example:If, we take
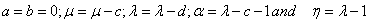 in (2.1) and making use of the following well-known result on both the sides of the resulting result of (2.1) (cf., e.g., Erdélyi et al.[4, p.185, Eqn. 13.1 (7)]):
in (2.1) and making use of the following well-known result on both the sides of the resulting result of (2.1) (cf., e.g., Erdélyi et al.[4, p.185, Eqn. 13.1 (7)]):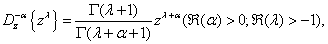 We easily arrive at the well-known Dougall’s formula[3, p. 7, Eqn. 1.4(1)] after a little simplification.
We easily arrive at the well-known Dougall’s formula[3, p. 7, Eqn. 1.4(1)] after a little simplification.ACKNOWLEDGEMENTS
- The authors are thankful to the referee for the valuable comments and suggestions, which have led the paper to the present form.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML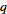 -Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 47-49, 1998.
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 47-49, 1998.