-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2012; 2(6): 217-220
doi: 10.5923/j.ajms.20120206.09
Common Fixed Point Results in Cone Metric Spaces Using Altering Distance Function
Tanmoy Som , Lokesh Kumar
Department of Applied Mathematics Indian Institute of Technology, Banaras Hindu University, Varanasi, 221005, India
Correspondence to: Lokesh Kumar , Department of Applied Mathematics Indian Institute of Technology, Banaras Hindu University, Varanasi, 221005, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Cone metric space was introduced by Huang Long-Guang et al. (2007) which generalized the concept of metric space. Several fixed point results have been proved in such spaces which generalized and extended the analogous results in metric spaces by different authors. In the present paper two common fixed point results for a sequence of self maps of a complete cone metric space, using altering distance function between the points under a certain continuous control function, are obtained, which generalize the results of Sastry et al. (2001) and Pandhare et al. (1998). Two examples are given in support of our results.
Keywords: Complete Cone Metric Space, Altering Distance Function, Common Fixed Point
Cite this paper: Tanmoy Som , Lokesh Kumar , "Common Fixed Point Results in Cone Metric Spaces Using Altering Distance Function", American Journal of Mathematics and Statistics, Vol. 2 No. 6, 2012, pp. 217-220. doi: 10.5923/j.ajms.20120206.09.
1. Introduction
- Results concerning the existence and properties of fixed points are known as fixed point theorems. The theory of fixed point became an important tool in non-linear functional analysis since 1930. It is used widely in applied mathematics. The existence and types of solution always help to give geometrical interpretation, to discuss the behavior and to check stability of the concern system. The famous Banach contraction principle says that “every contraction map from a complete metric space to itself has a unique fixed point”. Due to the wide importance and application of this principle, several authors generalized this principle using either different contractive conditions or space structure. Further, the study of common fixed points of mappings satisfying certain contractive conditions has been reinvestigated extensively by many mathematicians. The fixed point theorems related to altering distances between points in complete metric space have been obtained initially by D. Delbosco in 1967, F. Skof in 1977, M.S. Khan, M. Swaleh and S. Sessa in 1984.Recently, Huang Long-Guang et al. (2007) introduced the concept of cone metric spaces in which set of real numbers has been replaced by a real Banach space and a partial order has been defined with the help of a subset (called cone) of that real Banach space. As the set of real numbers is well ordered but the concerned Banach space is only partially ordered, so it is a task to extend the existing results in metric space to cone metric spaces if possible. In this paper we have established common fixed point results for cone metric spaces which generalize the existing results in metric spaces of Sastry et al.[9] and Pandhare et al.[4]. We now give some preliminaries about cone metric spaces given by Huang Long-Guang et al.[2].Let
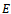 be a real Banach space and
be a real Banach space and 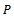 be a subset of
be a subset of 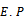 is called a cone if(i) is closed, non-empty and
is called a cone if(i) is closed, non-empty and 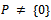 (ii)
(ii) 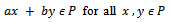 and non-negative real numbers
and non-negative real numbers 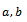 (iii)
(iii) 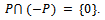 .For a given cone
.For a given cone 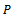 we can define a partial ordering
we can define a partial ordering 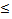 with respect to
with respect to 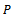 by
by 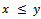 if and only if
if and only if 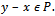
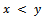 will stand for
will stand for 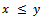 and
and 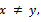 while
while 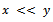 will stand for
will stand for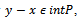 where
where 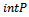 denotes the interior of
denotes the interior of 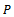 .The cone is called regular if every increasing and bounded above sequence
.The cone is called regular if every increasing and bounded above sequence 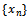 in
in 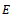 is convergent. Equivalently the cone
is convergent. Equivalently the cone 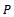 is regular if and only if every decreasing and bounded below sequence is convergent.Definition1.1[2] Let
is regular if and only if every decreasing and bounded below sequence is convergent.Definition1.1[2] Let 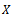 be a non-empty set. Suppose the mapping
be a non-empty set. Suppose the mapping 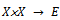 satisfies(i)
satisfies(i) 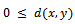 for all
for all 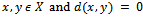 if and only if
if and only if 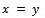 (ii)
(ii) 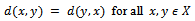 (iii)
(iii) 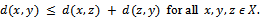 Then
Then 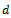 is called a cone metric on
is called a cone metric on 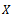 and
and 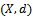 is called a cone metric space.Definition 1.2[2] Let
is called a cone metric space.Definition 1.2[2] Let 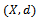 be a cone metric space,
be a cone metric space, 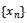 a sequence in
a sequence in 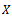 and
and 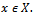 For every
For every 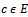 with
with 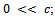 we say that
we say that 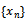 is:(i) a Cauchy sequence if there is a natural number
is:(i) a Cauchy sequence if there is a natural number 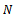 such that for all
such that for all 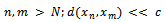 (ii) convergent to
(ii) convergent to 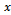 if there is a natural number
if there is a natural number 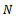 such that for all
such that for all 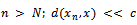 for some
for some 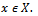
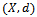 is called a complete cone metric space if every Cauchy sequence in
is called a complete cone metric space if every Cauchy sequence in 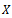 is convergent.Definition 1.3 Let
is convergent.Definition 1.3 Let 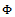 be the set of all continuous self maps
be the set of all continuous self maps 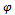 of
of 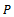 satisfying(i)
satisfying(i) 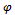 is monotone increasing(ii)
is monotone increasing(ii) 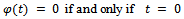 Then it is called an altering distance function on the cone
Then it is called an altering distance function on the cone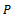 .
.2. Main Results
- In this section we obtain two fixed point results on a complete cone metric space generalizing Theorem 2 of Sastry and Babu[9] and Pandhare and Waghmode[4] in turn. Theorem 2.1 Let
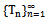 be sequence of self maps on complete cone metric space
be sequence of self maps on complete cone metric space 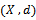 Assume that(i) There exist a
Assume that(i) There exist a 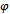 in
in 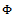 such that
such that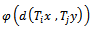
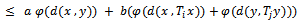 for all
for all 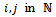 and for all distinct
and for all distinct 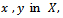 where
where 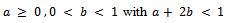 (ii) There is a point
(ii) There is a point 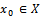 such that any two consecutive members of the sequence
such that any two consecutive members of the sequence 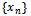 defined by
defined by 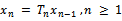 are distinct.Then
are distinct.Then 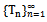 has a unique common fixed point in X. In fact
has a unique common fixed point in X. In fact 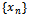 is Cauchy and the limit of
is Cauchy and the limit of 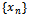 is the unique common fixed point of
is the unique common fixed point of 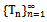 .Proof : Let
.Proof : Let 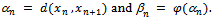 Then
Then 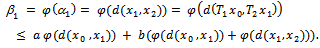 This implies that
This implies that 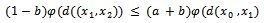 i.e.,
i.e., 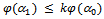 i.e.,
i.e., 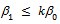 where
where 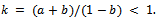 By induction, we get
By induction, we get 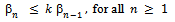 | (1) |
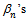 are decreasing and bounded below sequences in
are decreasing and bounded below sequences in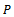 .As P is regular,
.As P is regular, 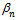 will converge and
will converge and 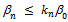 as n
as n 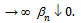 Now
Now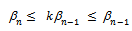
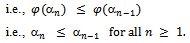 Therefore
Therefore 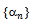 is a decreasing sequence in
is a decreasing sequence in 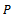 . As
. As 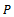 is regular
is regular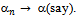 .Then
.Then 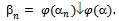 So that
So that 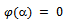 hence
hence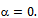
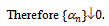 | (2) |
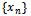 is Cauchy in
is Cauchy in 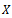 .If it is not so then there is a
.If it is not so then there is a 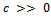 and sequences
and sequences 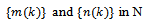 such that
such that 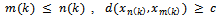 and
and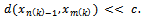 Assume that
Assume that 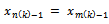 for infinitely many
for infinitely many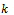 .Then for such
.Then for such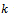 we have
we have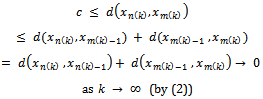 which is a contradiction because
which is a contradiction because 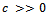 .Hence for large
.Hence for large 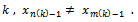 Consequently
Consequently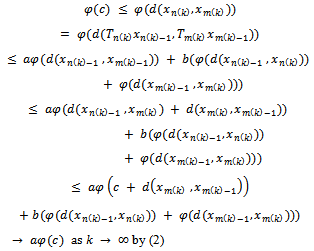 Hence
Hence 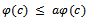 i.e.,
i.e., 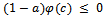 i.e.,
i.e., 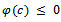 implying that
implying that 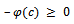 so
so 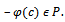 i.e.,
i.e., 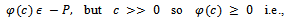
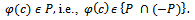 Therefore
Therefore 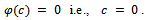 This is again a contradiction.Hence
This is again a contradiction.Hence 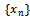 is a Cauchy sequence in
is a Cauchy sequence in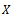 . As
. As 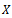 is complete, limit of
is complete, limit of 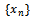 exists. Let it be
exists. Let it be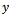 .There is a sequence
.There is a sequence 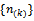 in N such that
in N such that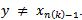 Otherwise
Otherwise 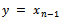 for large, which is not the case, since consecutive terms are different. With this subsequence
for large, which is not the case, since consecutive terms are different. With this subsequence 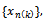 we have for any positive integer
we have for any positive integer 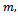
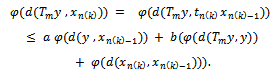 Taking limit
Taking limit
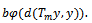 Since 0 < b < 1, it follows that
Since 0 < b < 1, it follows that 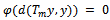 so that
so that 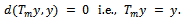 This shows that y is a fixed point of
This shows that y is a fixed point of 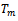 for each m. Thus
for each m. Thus 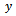 is a common fixed point for the sequence
is a common fixed point for the sequence 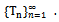 .Now we show that the fixed point is unique. Let
.Now we show that the fixed point is unique. Let 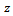 be another common fixed point of
be another common fixed point of 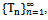 then
then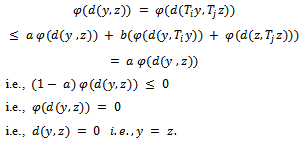 Remark: If we take metric as the usual metric and cone
Remark: If we take metric as the usual metric and cone 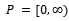 in our theorem then we get Theorem 2 of Sastry and Babu[9] as a corollary.Now we give our next result where
in our theorem then we get Theorem 2 of Sastry and Babu[9] as a corollary.Now we give our next result where 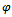 satisfies an additional property given by
satisfies an additional property given by 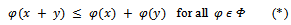 Theorem 2.2 Let
Theorem 2.2 Let 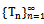 be a sequence of self maps on a complete cone metric space
be a sequence of self maps on a complete cone metric space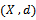 Assume that(i)There exist a
Assume that(i)There exist a 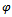 in
in 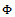 with (*) such that
with (*) such that 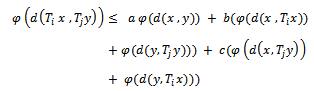 for all
for all 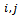 in
in 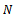 and for all distinct
and for all distinct 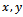 in
in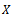 , where
, where 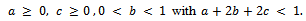 (ii) There is a point
(ii) There is a point 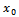 in
in 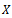 such that any two consecutive members of the sequence
such that any two consecutive members of the sequence 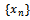 defined by
defined by 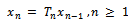 are distinct.Then
are distinct.Then 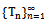 has a unique common fixed point in
has a unique common fixed point in 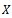 . In fact
. In fact 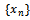 is Cauchy and the limit point of
is Cauchy and the limit point of 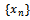 is the unique common fixed point of
is the unique common fixed point of 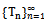 .Proof : Write
.Proof : Write 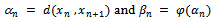 From (i) and (ii) , we have
From (i) and (ii) , we have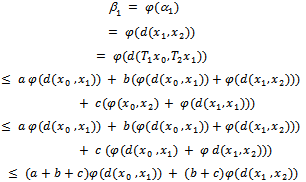 This implies that
This implies that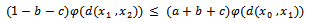 i.e.,
i.e., 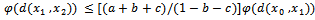 i.e.,
i.e., 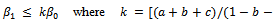
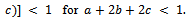 By induction it follows that
By induction it follows that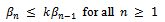 | (3) |
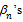 are decreasing and bounded below sequences in
are decreasing and bounded below sequences in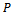 .As
.As  is regular cone,
is regular cone, 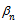 will converge and
will converge and 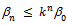
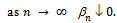 Now
Now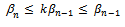
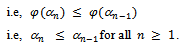 Therefore
Therefore 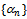 is a decreasing sequence in
is a decreasing sequence in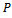 . As
. As 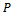 is regular
is regular 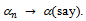 Then
Then 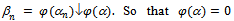 hence
hence 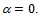
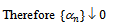 | (4) |
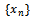 is Cauchy in
is Cauchy in 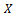 . If it is not so, then there is a
. If it is not so, then there is a 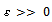 and sequences
and sequences 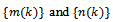 in
in 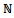 such that
such that 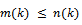 and
and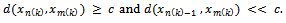 Assume that,
Assume that, 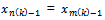 for infinitely many
for infinitely many 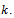 Then for such
Then for such 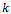 we have
we have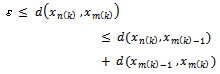
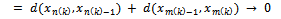 as
as 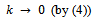 which is a contradiction because
which is a contradiction because 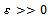 .Hence for large
.Hence for large 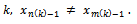 Consequently
Consequently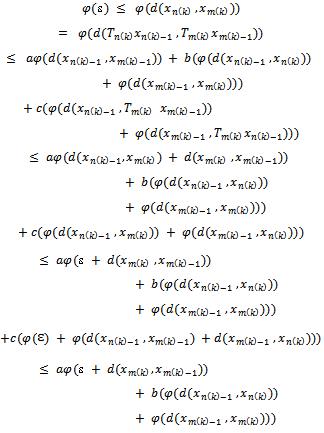
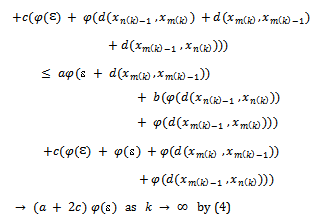 Hence
Hence 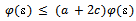
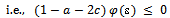 i.e.,
i.e., 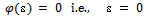 . This is again a contradiction.Hence
. This is again a contradiction.Hence 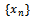 is Cauchy sequence in
is Cauchy sequence in 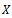 . As
. As 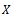 is complete, limit of
is complete, limit of 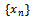 exists. Let it be
exists. Let it be 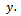 There is a sequence
There is a sequence 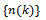 such that
such that 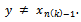 Otherwise
Otherwise 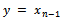 for large
for large 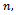 which is not the case, since the consecutive terms are different. With this subsequence
which is not the case, since the consecutive terms are different. With this subsequence 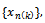 we have for any positive integer
we have for any positive integer 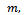
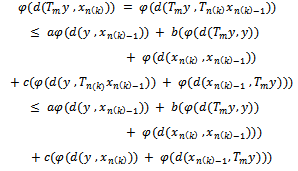 Taking limit as
Taking limit as 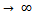 , we have
, we have 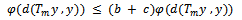 i.e.,
i.e., 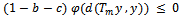 i.e.,
i.e., 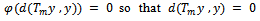 i.e.,
i.e., 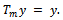 This shows that
This shows that 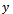 is a fixed point of
is a fixed point of 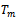 . Thus
. Thus 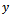 is a common fixed point for the sequence
is a common fixed point for the sequence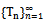 . The uniqueness of the common fixed point can be shown easily.
. The uniqueness of the common fixed point can be shown easily. 3. Examples
- Example 3.1: Let
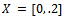 with usual metric. Define
with usual metric. Define 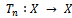 by
by 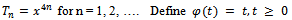 so that
so that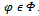 . Then
. Then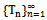 satisfies the condition (i) with
satisfies the condition (i) with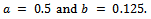 Observe that, for any non-zero
Observe that, for any non-zero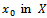 , the sequence
, the sequence 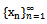 defined by
defined by 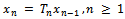 has all its elements distinct so (ii) also holds; thus hypothesis of Theorem2.1 is satisfied and
has all its elements distinct so (ii) also holds; thus hypothesis of Theorem2.1 is satisfied and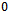 is the unique common fixed point of
is the unique common fixed point of 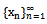 .Example 3.2: Let
.Example 3.2: Let 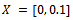 with usual metric. Define
with usual metric. Define 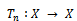 by
by 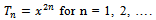 Define
Define 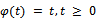 so that
so that 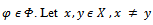 Then,
Then,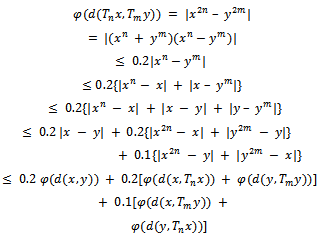 If we take
If we take 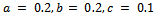 Then
Then 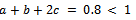 Hence condition (i) of Theorem 2.2 is satisfied. Observe that for any non zero
Hence condition (i) of Theorem 2.2 is satisfied. Observe that for any non zero 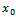 in
in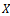 , the sequence
, the sequence 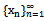 defined by
defined by 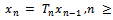 has all its elements distinct so the condition (ii) of Theorem 2.2 also holds and
has all its elements distinct so the condition (ii) of Theorem 2.2 also holds and 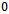 is the unique common fixed point.
is the unique common fixed point. 4. Conclusions
- The results obtained in this work extends the common fixed point results in metric spaces of Sastry and Babu[9] and Pandhare and Waghmode[4] to cone metric space in a more general setting in context with the space structure equipped with a partial order.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML