-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2012; 2(6): 213-216
doi: 10.5923/j.ajms.20120206.08
Some Fixed Point Results in 2-Metric Spaces
Amalendu Choudhury 1, T. Som 2
1Department of Mathematics and Statistics Haflong Govt. College, Haflong, Dima Hasao Assam. Pin, 788819, India
2Department of Applied Mathematics Indian Institute of Technology (BHU), Varanasi, 221005, India
Correspondence to: Amalendu Choudhury , Department of Mathematics and Statistics Haflong Govt. College, Haflong, Dima Hasao Assam. Pin, 788819, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The present paper deals with few fixed point results for mappings satisfying some generalized contractive type inequality condition in 2-metric spaces, which generalize the results of Rhoades (1979) and Gahler (1963), Iseki (1975), Iseki et.al (1976) in turn. The inqualities involve a rational type of terms given by 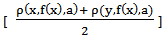 ,
, 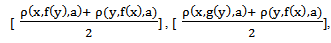 , [ρ(x,fjmj(y),a) + ρ(y,fimi(x),a)] /2 etc under max composition.
, [ρ(x,fjmj(y),a) + ρ(y,fimi(x),a)] /2 etc under max composition.
Keywords: 2- Metric Space, Self Mapping, Generalized Contraction, Fixed Point
Cite this paper: Amalendu Choudhury , T. Som , "Some Fixed Point Results in 2-Metric Spaces", American Journal of Mathematics and Statistics, Vol. 2 No. 6, 2012, pp. 213-216. doi: 10.5923/j.ajms.20120206.08.
1. Introduction
- The concept of a 2- metric space was initially given by Gahler ([2],[3]) during 1960’s. Then about a decade after during 1970’s some basic fixed point results in such spaces have been established by Iseki ([4], [5]). There after some fixed point results are obtained in such spaces by Khan et al [6], Rhoades[7] and many others extending the fixed point results for contractive mappings from metric space to 2- metric space. In this subsection we give some preliminary definitions and results of aforesaid authors.Definition 1.1 A 2-metric space is a space X in which, for each triple of points a, b, c there exists a real valued non negative function satisfying:(1) For each pair of points a, b, a ≠ b of X, there exists a point c ε X such that ρ(a, b,c) ≠ 0.(2) ρ(a, b, c) = 0 when at least two of the points are equal. (3) ρ(a, b, c) = ρ(a, c, b) = ρ(b, c, a) and (4) ρ(a, b, c) ≤ ρ(a, b, d) + ρ(a, d, c) + ρ(d, b, c)Definition 1.2 A sequence {xn} of X is called Cauchy sequence if lim ρ(xn , xm ,a) = 0 for all a ε X. Definition 1.3 A sequence {xn} in X is convergent and x ε X is the limit of this sequence if ρ(xn, x ,a) = 0 for each a ε X. Theorem 1.1 (Rhoades[7]) Let X be a complete 2-metric Space, f: X → X satisfying: there exists a h, 0 ≤ h < 1 such ρ(f(x), f(y), a) ≤ h max {ρ(x, y, a), ρ(x, f(x), a), ρ(y, f(y), a), ρ (x,f(y),a), ρ (y,f(x),a)}that for each x, y, a ε X Then f possesses a unique fixed point z and lim f n(x0) = z for each x0 ε X.Theorem 1.2 (Rhoades[7]) Let f and g be mappings of a complete 2– metric space X into itself satisfyingρ(f(x),g(y),a) ≤ h max {ρ(x,y,a), ρ(x,f(x),a), ρ(y,g(y),a), ρ(y,f(x),a), ρ(x,g(y),a)}for all x,y ε X, h a fixed constant satisfying 0 ≤ h <1. Then f and g have a common fixed point z. Theorem 1.3 (Rhoades[7]) Let X be a complete 2– metric space , {fn}, n = 1,2,…. a sequence of mapping fn : X → X, suppose there exists a sequence of non negative integers {mn} and a number h, 0 ≤ h < 1 such that, for all x,y ∈ X and every pair i, j , i ≠ j and satisfying ρ(fimi(x),fjmj(y),a) ≤ h max {ρ(x,y,a), ρ(x,fimi(x),a),ρ(y,fjmj(y),a), ρ(y,fimi(x),a)} Then the mappings {fn} have a unique common fixed point.
2. Objective
- The main objective of the paper is to establish few fixed point results in 2-metric space involving terms like [
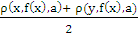 ], [
], [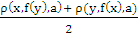 ] , [
] , [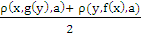 ] , [ρ(x,fjmj(y),a) + ρ(y,fimi(x),a)]/2 etc in the inequality condition under max composition, which is more general than the inequality condition used by previous authors.
] , [ρ(x,fjmj(y),a) + ρ(y,fimi(x),a)]/2 etc in the inequality condition under max composition, which is more general than the inequality condition used by previous authors. 3. Method
- The usual fixed point analysis methods for 2-metric space as used by earlier authors Gahler, Rhoades, Iseki has been used to prove our generalizations.
4. Main Results
- In this paper few fixed point results are obtained for some generalized contractive mappings involving rational type terms in a 2- metric space. Taking a clue from Theorem 1.1, our first result goes as follows:Theorem 4.1 Let X be a complete 2– metric space, f : X → X satisfying : there exists a h, 0 ≤ h < 1 such that for each x, y, a ε X, ρ( f(x),f(y),a) ≤ h max {ρ(x,y,a), ρ(x, f(x),a), ρ(y,f(y),a), [
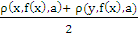 ], [
], [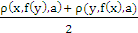 ] } (i) Then f possesses a unique fixed point z.Proof : Let x0 ∈ X and define {xn} by xn+1 = f(xn), n = 0,1,2.. . From (i) we have ,ρ(xn+1, xm+1,a) = ρ(f(xn), f(xm),a) ≤ h max { ρ(xn,xm,a), ρ(xn,xn+1,a), ρ(xm,xm+1,a), [
] } (i) Then f possesses a unique fixed point z.Proof : Let x0 ∈ X and define {xn} by xn+1 = f(xn), n = 0,1,2.. . From (i) we have ,ρ(xn+1, xm+1,a) = ρ(f(xn), f(xm),a) ≤ h max { ρ(xn,xm,a), ρ(xn,xn+1,a), ρ(xm,xm+1,a), [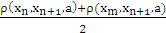 ], [
], [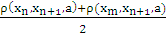 ]}≤ h ρ(xn,xm,a)It cannot be that, ρ(xn,xm+1,a)/2 ≥ ρ(xn, xm,a) , ρ(xn+1, xm+1, a)Again ,ρ(xn,xm+1,a) ≤ ρ(xn,xm+1,xn+1) + ρ(xn,xn+1,a) + ρ(xn+1,xm+1,a)and we have , ρ(xn,xm+1,xn+1) = 0. Thus, ρ(xn+1,xm+1,a) ≤ h ρ(xn, xm, a)Similarly, ρ(xn,xm,a) ≤ h ρ(xn-1, xm-1,a)≤ h2 ρ(xn-2, xm-2,a)…………… ≤ hn ρ(x0, xk,a)Therefore for integers n, m where n > m ≥ 0, ρ(xn, xm, a) ≤ hn ρ(x0, xk,a) (ii)where k is a suitable integer satisfying 0 < k ≤ m. using property 4 of definition 1 and (ii),we get ρ(x0, xk,a) ≤ ρ(x0, xk,x1) + ρ(x0, x1,a) + ρ(x1, xk, a) ≤ ρ(x0, xk, x1) + ρ(x0, x1, a) + h ρ(x0, xk, a) ≤ ……………… ≤
]}≤ h ρ(xn,xm,a)It cannot be that, ρ(xn,xm+1,a)/2 ≥ ρ(xn, xm,a) , ρ(xn+1, xm+1, a)Again ,ρ(xn,xm+1,a) ≤ ρ(xn,xm+1,xn+1) + ρ(xn,xn+1,a) + ρ(xn+1,xm+1,a)and we have , ρ(xn,xm+1,xn+1) = 0. Thus, ρ(xn+1,xm+1,a) ≤ h ρ(xn, xm, a)Similarly, ρ(xn,xm,a) ≤ h ρ(xn-1, xm-1,a)≤ h2 ρ(xn-2, xm-2,a)…………… ≤ hn ρ(x0, xk,a)Therefore for integers n, m where n > m ≥ 0, ρ(xn, xm, a) ≤ hn ρ(x0, xk,a) (ii)where k is a suitable integer satisfying 0 < k ≤ m. using property 4 of definition 1 and (ii),we get ρ(x0, xk,a) ≤ ρ(x0, xk,x1) + ρ(x0, x1,a) + ρ(x1, xk, a) ≤ ρ(x0, xk, x1) + ρ(x0, x1, a) + h ρ(x0, xk, a) ≤ ……………… ≤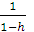 ρ(x0, x1, a)Therefore, ρ(xn, xm, a) ≤
ρ(x0, x1, a)Therefore, ρ(xn, xm, a) ≤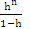 ρ(x0, x1, a)So it can be easily shown that ρ(x0, xk, x1) = 0 , (see[7]) where k/ is a suitable integer satisfying 0≤ k/≤ k. Therefore {xn} is Cauchy sequence, hence convergent. Let us consider the limit z, using (i), for any a ε X.ρ( xn+1, f(z), a) = ρ ( f(z),a, xn+1) = ρ( f(z), xn+1, a) ≤ h max{ ρ( z, xn, a), ρ(z, f(z), a), ρ(xn, xn+1, a), [
ρ(x0, x1, a)So it can be easily shown that ρ(x0, xk, x1) = 0 , (see[7]) where k/ is a suitable integer satisfying 0≤ k/≤ k. Therefore {xn} is Cauchy sequence, hence convergent. Let us consider the limit z, using (i), for any a ε X.ρ( xn+1, f(z), a) = ρ ( f(z),a, xn+1) = ρ( f(z), xn+1, a) ≤ h max{ ρ( z, xn, a), ρ(z, f(z), a), ρ(xn, xn+1, a), [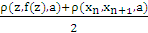 ], [
], [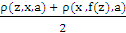 ] }Taking the limit of both sides as n → ∞, we have, ρ(z, f(z),a) ≤ h ρ(z, f(z),a)which implies z = f(z). Suppose z, w are fixed points of f. Then from (i), each a ε X, we haveρ(z, w, a) ≤ h ρ(z, w, a). Since 0 ≤ h < 1, and using ρ(a, b, c) ≠ 0.So we get, z = w. Therefore f has a unique fixed point z. Theorem 4.2 Let X be a complete 2- metric space, {fn} a sequence of mappings of X into X with fixed points zn, and f a mappings of X into X satisfying ρ(f(x),f(y),a) ≤ h max {ρ(x,y,a), ρ(x,f(x),a), ρ(y,f(y),a), ρ(x,f(y),a), ρ(y,f(x),a)} (iii) with fixed point z, such that fn → f uniformly on { zn : n = 1,2, ….}. Then zn → z.Proof: Let ε > 0. From the uniform convergence of {fn} on {zn : n = 1,2,..} there exists an integer N such that for all n ≥ N, ρ( f(zn), fn(zn), a) <
] }Taking the limit of both sides as n → ∞, we have, ρ(z, f(z),a) ≤ h ρ(z, f(z),a)which implies z = f(z). Suppose z, w are fixed points of f. Then from (i), each a ε X, we haveρ(z, w, a) ≤ h ρ(z, w, a). Since 0 ≤ h < 1, and using ρ(a, b, c) ≠ 0.So we get, z = w. Therefore f has a unique fixed point z. Theorem 4.2 Let X be a complete 2- metric space, {fn} a sequence of mappings of X into X with fixed points zn, and f a mappings of X into X satisfying ρ(f(x),f(y),a) ≤ h max {ρ(x,y,a), ρ(x,f(x),a), ρ(y,f(y),a), ρ(x,f(y),a), ρ(y,f(x),a)} (iii) with fixed point z, such that fn → f uniformly on { zn : n = 1,2, ….}. Then zn → z.Proof: Let ε > 0. From the uniform convergence of {fn} on {zn : n = 1,2,..} there exists an integer N such that for all n ≥ N, ρ( f(zn), fn(zn), a) <  , for all zn , where M =
, for all zn , where M = 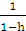 Now, ρ(zn, z, a) = ρ( fn(zn), f(z),a) ≤ ρ(fn(zn),f(z),f(zn) +ρ(fn(zn), f(zn),a) + ρ(f(zn),f(z),a) (iv)Again from (iii), ρ(f(zn),f(z),a) ≤ h max{ρ(zn,z,a),ρ(zn,f(zn),a),ρ(z,f(z),a),ρ(zn,f(z),a)ρ(z,f(zn),a)}≤ h max{ρ(zn, z, a), ρ(zn, f(zn),a)}so thatρ(fn(zn), f(z), f(zn)) = ρ(f(z), f(zn),zn) ≤ h max {ρ(zn, z, zn), ρ(zn, f(zn),zn)} = 0.Now (iv) becomes ρ(zn, z, a) ≤ ρ(fn(zn),f(zn),a) + h max{ρ( zn, z, a), ρ(zn, f(zn),a)}which implies ρ( zn, z, a) ≤
Now, ρ(zn, z, a) = ρ( fn(zn), f(z),a) ≤ ρ(fn(zn),f(z),f(zn) +ρ(fn(zn), f(zn),a) + ρ(f(zn),f(z),a) (iv)Again from (iii), ρ(f(zn),f(z),a) ≤ h max{ρ(zn,z,a),ρ(zn,f(zn),a),ρ(z,f(z),a),ρ(zn,f(z),a)ρ(z,f(zn),a)}≤ h max{ρ(zn, z, a), ρ(zn, f(zn),a)}so thatρ(fn(zn), f(z), f(zn)) = ρ(f(z), f(zn),zn) ≤ h max {ρ(zn, z, zn), ρ(zn, f(zn),zn)} = 0.Now (iv) becomes ρ(zn, z, a) ≤ ρ(fn(zn),f(zn),a) + h max{ρ( zn, z, a), ρ(zn, f(zn),a)}which implies ρ( zn, z, a) ≤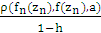 < ε. Thus zn → z.Our next result generalizes theorem 1.2 of Rhoades[7].Theorem 4.3 Let f and g be mappings of a complete 2–metric space X into itself satisfyingρ(f(x),g(y),a) ≤ h max {ρ(x,y,a), ρ(x,f(x),a), ρ(y,g(y),a), ρ(y,f(x),a), ρ(x,g(y),a),[
< ε. Thus zn → z.Our next result generalizes theorem 1.2 of Rhoades[7].Theorem 4.3 Let f and g be mappings of a complete 2–metric space X into itself satisfyingρ(f(x),g(y),a) ≤ h max {ρ(x,y,a), ρ(x,f(x),a), ρ(y,g(y),a), ρ(y,f(x),a), ρ(x,g(y),a),[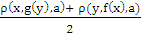 ]} (v)for all x,y ε X, h a fixed constant satisfying 0 ≤ h <1 . Then f and g have a common fixed point z and (fg)n(x0) → z and (gf)n(x0) → z for each x0 ε X.Proof: Let x0 ε X and we define {xn} by x2n+1 = f(x2n) and x2n+2 = g(x2n+1)From (vii), we get ρ(x2n+1, x2n+2, a) = ρ(f(x2n), g(x2n+1), a) ≤ h max {ρ(x2n,x2n+1,a), ρ(x2n,x2n+1,a), ρ(x2n+1,x2n+2,a), ρ(x2n+1,x2n+1,a), ρ(x2n,x2n+2,a), [
]} (v)for all x,y ε X, h a fixed constant satisfying 0 ≤ h <1 . Then f and g have a common fixed point z and (fg)n(x0) → z and (gf)n(x0) → z for each x0 ε X.Proof: Let x0 ε X and we define {xn} by x2n+1 = f(x2n) and x2n+2 = g(x2n+1)From (vii), we get ρ(x2n+1, x2n+2, a) = ρ(f(x2n), g(x2n+1), a) ≤ h max {ρ(x2n,x2n+1,a), ρ(x2n,x2n+1,a), ρ(x2n+1,x2n+2,a), ρ(x2n+1,x2n+1,a), ρ(x2n,x2n+2,a), [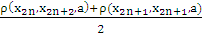 ] } ≤ h max { ρ(x2n,x2n+1,a), ρ(x2n, x2n+2,a)}Again , ρ(x2n,x2n+2,a) ≤ ρ(x2n,x2n+2,x2n+1) + ρ(x2n,x2n+1,a) + ρ(x2n+1,x2n+2,a)and we have ,ρ(x2n,x2n+2,x2n+1) = 0. Thus, ρ(x2n+1,x2n+2,a) ≤ h ρ(x2n, x2n+1, a)Similarly, ρ(x2n,x2n+1,a) ≤ h ρ (x2n-1, x2n,a)For arbitrary n, we have ρ(xn, xn+1, a) ≤ hn ρ(x0, x1, a) (vi) For any m > n and using property 4 of definition 1 and (vi)ρ(xm, xn,a) ≤
] } ≤ h max { ρ(x2n,x2n+1,a), ρ(x2n, x2n+2,a)}Again , ρ(x2n,x2n+2,a) ≤ ρ(x2n,x2n+2,x2n+1) + ρ(x2n,x2n+1,a) + ρ(x2n+1,x2n+2,a)and we have ,ρ(x2n,x2n+2,x2n+1) = 0. Thus, ρ(x2n+1,x2n+2,a) ≤ h ρ(x2n, x2n+1, a)Similarly, ρ(x2n,x2n+1,a) ≤ h ρ (x2n-1, x2n,a)For arbitrary n, we have ρ(xn, xn+1, a) ≤ hn ρ(x0, x1, a) (vi) For any m > n and using property 4 of definition 1 and (vi)ρ(xm, xn,a) ≤ 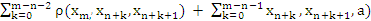 = hn(1-h)-1.[ρ(x0, x1, xm) + ρ(x0, x1, a)]we can easily shown that, ρ(x0, x1, xm) = 0. ([7] )So that {xn} is a Cauchy sequence and hence convergent.Let us consider the limit z.Now, ρ(f(z), z, a) ≤ ρ(f(z), z, x2n+2) + ρ(f(z), x2n+2, a) + ρ(x2n+2, z, a) (vii)From (vii), we get ρ(f(z), x2n+2, a) = ρ(f(z), g(x2n+1), a) ≤ h max{ ρ(z, x2n+1, a), ρ(z, f(z), a), ρ(x2n+1, x2n+2, a), ρ(x2n+1,f(z),a), ρ(z,x2n+2,a), [
= hn(1-h)-1.[ρ(x0, x1, xm) + ρ(x0, x1, a)]we can easily shown that, ρ(x0, x1, xm) = 0. ([7] )So that {xn} is a Cauchy sequence and hence convergent.Let us consider the limit z.Now, ρ(f(z), z, a) ≤ ρ(f(z), z, x2n+2) + ρ(f(z), x2n+2, a) + ρ(x2n+2, z, a) (vii)From (vii), we get ρ(f(z), x2n+2, a) = ρ(f(z), g(x2n+1), a) ≤ h max{ ρ(z, x2n+1, a), ρ(z, f(z), a), ρ(x2n+1, x2n+2, a), ρ(x2n+1,f(z),a), ρ(z,x2n+2,a), [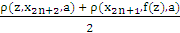 ]} (viii)Substituting (vii) into (viii) and taking limit as n → ∞, we have,ρ(f(z), z, a) ≤ h ρ(z, f(z), a) as 0 ≤ h < 1 , we get z = f(z).Therefore, z is a fixed point of f. Similarly, we can show that z is also a fixed point of g. For uniqueness, suppose z and w are common fixed points of f and g.Now from (v) ρ(z, w, a) = ρ(f(z), g(w), a) ≤ h max {ρ(z, w, a), ρ(z,f(z),a), ρ(w,g(w),a),ρ(z,g(w),a),ρ(w,f(z),a),[
]} (viii)Substituting (vii) into (viii) and taking limit as n → ∞, we have,ρ(f(z), z, a) ≤ h ρ(z, f(z), a) as 0 ≤ h < 1 , we get z = f(z).Therefore, z is a fixed point of f. Similarly, we can show that z is also a fixed point of g. For uniqueness, suppose z and w are common fixed points of f and g.Now from (v) ρ(z, w, a) = ρ(f(z), g(w), a) ≤ h max {ρ(z, w, a), ρ(z,f(z),a), ρ(w,g(w),a),ρ(z,g(w),a),ρ(w,f(z),a),[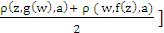 } ≤ h max { ρ(z,w,a), 0 ,0 ,ρ(z,w,a), ρ(w,z,a),ρ(z,w,a)}or, ρ(z,w,a) ≤ h ρ(z,w,a), which implies z = w. Thus z is a unique common fixed point of f and g . An extension of theorem 1.3 of Rhoades[7] goes as follows:Theorem 4.4 Let X be a complete 2–metric space , {fn}, n = 1,2,…. a sequence of mapping fn: X → X, suppose there exists a sequence of non negative integers {mn} and a number h, 0 ≤ h < 1 such that, for all x,y ε X and every pair i ,j , i ≠ j and satisfyingρ(fimi(x),fjmj(y),a) ≤ h max {ρ(x,y,a), ρ(x,fimi(x),a),ρ(y,fjmj(y),a), ρ(y,fimi(x),a), ρ(x,fjmj(y), [ρ(x,fjmj(y),a) + ρ(y,fimi(x),a)] /2 } (ix) Then the mappings {fn} have a unique common fixed point.Proof : Taking gi = fimi, i = 1,2,3,…. in (ix), we have ρ(gi(x), gj(y),a) ≤ h max {ρ(x,y,a), ρ(x,gi(x),a), ρ(y,gj(y),a), ρ(y,gi(x),a), ρ(x,gj(y),a), [
} ≤ h max { ρ(z,w,a), 0 ,0 ,ρ(z,w,a), ρ(w,z,a),ρ(z,w,a)}or, ρ(z,w,a) ≤ h ρ(z,w,a), which implies z = w. Thus z is a unique common fixed point of f and g . An extension of theorem 1.3 of Rhoades[7] goes as follows:Theorem 4.4 Let X be a complete 2–metric space , {fn}, n = 1,2,…. a sequence of mapping fn: X → X, suppose there exists a sequence of non negative integers {mn} and a number h, 0 ≤ h < 1 such that, for all x,y ε X and every pair i ,j , i ≠ j and satisfyingρ(fimi(x),fjmj(y),a) ≤ h max {ρ(x,y,a), ρ(x,fimi(x),a),ρ(y,fjmj(y),a), ρ(y,fimi(x),a), ρ(x,fjmj(y), [ρ(x,fjmj(y),a) + ρ(y,fimi(x),a)] /2 } (ix) Then the mappings {fn} have a unique common fixed point.Proof : Taking gi = fimi, i = 1,2,3,…. in (ix), we have ρ(gi(x), gj(y),a) ≤ h max {ρ(x,y,a), ρ(x,gi(x),a), ρ(y,gj(y),a), ρ(y,gi(x),a), ρ(x,gj(y),a), [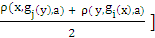 } (x)Let us consider x0 ε X and we define xn = gn(xn-1), n = 1,2,…Now from (x), we get ρ(xn, xn+1,a) = ρ( gn(xn-1), gn+1(xn),a)≤ h max { ρ(xn-1,xn,a), ρ(xn-1,xn,a), ρ(xn,xn+1,a),ρ(xn,xn,a), ρ(xn-1,xn+1,a), [
} (x)Let us consider x0 ε X and we define xn = gn(xn-1), n = 1,2,…Now from (x), we get ρ(xn, xn+1,a) = ρ( gn(xn-1), gn+1(xn),a)≤ h max { ρ(xn-1,xn,a), ρ(xn-1,xn,a), ρ(xn,xn+1,a),ρ(xn,xn,a), ρ(xn-1,xn+1,a), [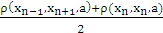 ]}≤ h max { ρ(xn-1,xn,a), ρ(xn-1,xn,a), ρ(xn,xn+1,a),0, ρ(xn-1,xn+1,a),
]}≤ h max { ρ(xn-1,xn,a), ρ(xn-1,xn,a), ρ(xn,xn+1,a),0, ρ(xn-1,xn+1,a), 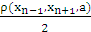 }as in the proof of Theorem 2.3, we led to the conclusion that ρ(x2n,x2n+1,a) ≤ h ρ(x2n-1,x2n,a)and in general ρ(xn,xn+1,a) ≤ hn ρ(x0,x1,a).Therefore, {xn} is Cauchy sequence and converges to a limit z. Now we get from (x), ρ(gn(x),gm+1(xm),a) ≤ h max { ρ(z,xm,a), ρ(z,gn(z),a), ρ(xm,xm+1,a), ρ(xm,gn(z),a), ρ(z,xm+1,a),
}as in the proof of Theorem 2.3, we led to the conclusion that ρ(x2n,x2n+1,a) ≤ h ρ(x2n-1,x2n,a)and in general ρ(xn,xn+1,a) ≤ hn ρ(x0,x1,a).Therefore, {xn} is Cauchy sequence and converges to a limit z. Now we get from (x), ρ(gn(x),gm+1(xm),a) ≤ h max { ρ(z,xm,a), ρ(z,gn(z),a), ρ(xm,xm+1,a), ρ(xm,gn(z),a), ρ(z,xm+1,a), 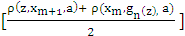 }Taking limit as m → ∞, we obtain, ρ(gn(z),z,a) ≤ h ρ(gn(z),z,a) = h ρ(z,gn(z),a) which implies that gn(z) = z, as 0 ≤ h < 1.For each n, we have fn(z) = fn(gn(z)) = fn(fnmnz), which shows that fn(z) is a fixed point of gn. Uniqueness of this theorem follows easily from (ix) and by uniqueness, we have fn(z) = z .Hence z is a unique common fixed point of fn. Theorem 4.5 Let T and S be two self mappings of a complete metric space (X,d) satisfying ad(Tx,Sy,u) + bd(x,Tx,u) + cd(y,Sy,u) ≤ q max{d(x,y,u), d(x,Tx,u), d(y,Sy,u)} (xi) for x, y ε X and u ε X; a + c > q and a > q . Then T and S have a unique common fixed point.Proof: Let x0 ε X and we define {xn} by x2n+1 = Tx2n and x2n+2 = Sx2n+1. Now putting x = x2n and y = x2n+1 in (xi) we havead(Tx2n, Sx2n+1, u) + bd(x2n, Tx2n, u) + cd(x2n+1, Sx2n+1, u) ≤ q max{d(x2n, x2n+1, u), d(x2n, Tx2n, u), d(x2n+1,Sx2n+1,u)}or, ad(x2n+1, x2n+2, u) + bd(x2n, x2n+1, u) + cd(x2n+1, x2n+2, u) ≤ q max{d(x2n, x2n+1, u), d(x2n, x2n+1, u), d(x2n+1, x2n+2,u)}or, (a+c) d(x2n+1, x2n+2, u) + bd(x2n, x2n+1, u) ≤ qd(x2n, x2n+1, u)or, d(x2n+1, x2n+2, u) ≤
}Taking limit as m → ∞, we obtain, ρ(gn(z),z,a) ≤ h ρ(gn(z),z,a) = h ρ(z,gn(z),a) which implies that gn(z) = z, as 0 ≤ h < 1.For each n, we have fn(z) = fn(gn(z)) = fn(fnmnz), which shows that fn(z) is a fixed point of gn. Uniqueness of this theorem follows easily from (ix) and by uniqueness, we have fn(z) = z .Hence z is a unique common fixed point of fn. Theorem 4.5 Let T and S be two self mappings of a complete metric space (X,d) satisfying ad(Tx,Sy,u) + bd(x,Tx,u) + cd(y,Sy,u) ≤ q max{d(x,y,u), d(x,Tx,u), d(y,Sy,u)} (xi) for x, y ε X and u ε X; a + c > q and a > q . Then T and S have a unique common fixed point.Proof: Let x0 ε X and we define {xn} by x2n+1 = Tx2n and x2n+2 = Sx2n+1. Now putting x = x2n and y = x2n+1 in (xi) we havead(Tx2n, Sx2n+1, u) + bd(x2n, Tx2n, u) + cd(x2n+1, Sx2n+1, u) ≤ q max{d(x2n, x2n+1, u), d(x2n, Tx2n, u), d(x2n+1,Sx2n+1,u)}or, ad(x2n+1, x2n+2, u) + bd(x2n, x2n+1, u) + cd(x2n+1, x2n+2, u) ≤ q max{d(x2n, x2n+1, u), d(x2n, x2n+1, u), d(x2n+1, x2n+2,u)}or, (a+c) d(x2n+1, x2n+2, u) + bd(x2n, x2n+1, u) ≤ qd(x2n, x2n+1, u)or, d(x2n+1, x2n+2, u) ≤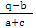 d(x2n, x2n+1, u) = h d(x2n, x2n+1, u), where h =
d(x2n, x2n+1, u) = h d(x2n, x2n+1, u), where h = 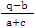 Similarly, d(x2n, x2n+1, u) ≤ h d(x2n-1, x2n, u) Therefore for any arbitrary nd(xn, xn+1, u) ≤ hn d(x0, x1, u) (xii)From (xii) using the property (4) of definition 1, we get, for any m > nd(xm, xn,u) ≤
Similarly, d(x2n, x2n+1, u) ≤ h d(x2n-1, x2n, u) Therefore for any arbitrary nd(xn, xn+1, u) ≤ hn d(x0, x1, u) (xii)From (xii) using the property (4) of definition 1, we get, for any m > nd(xm, xn,u) ≤ 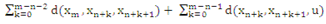 ≤ hn (1-h)-1[d(x0, x1, xm) + d(x0, x1, u)]We can easily shown that d(x0, x1, xm) = 0 ( Rhoades[7] )So that {xn} is a Cauchy sequence, hence convergent and {Tx2n},{Sx2n+1} also converge to z. From (xi), ad(Tx2n, Sz, u) + bd(x2n, Tx2n, u) + cd(z, Sz, u)≤ q max{d(x2n, z, u), d(x2n, Tx2n, u), d(z, Sz, u)}In the limiting case, we get ad(z, Sz, u) + cd(z, Sz, u) ≤ qd(z, Sz, u)or, (a + c -q) d(z, Sz, u) ≤ 0.Therefore, Sz = z since a+c > q.Thus z is a fixed point of S. Similarly we can show that z is also a fixed point of T. Hence z is a common fixed point of T and S.The uniqueness of the common fixed point can be easily shown by using (xi). This completes the proof of the theorem. Omitting the term bd(x,Tx,u) and cd(y,Sy,u) from the left hand side of theorem 4.5 we get the following result as a corollary of the above Theorem.Corollary 4.1 Let the self mappings T and S of a complete metric space (X, d) satisfyd(Tx, Sy, u) ≤ q max{d(x, y, u), d(x, Tx, u), d(y, Sy, u)} for x, y, u ε X. Then T and S have a unique common fixed point.
≤ hn (1-h)-1[d(x0, x1, xm) + d(x0, x1, u)]We can easily shown that d(x0, x1, xm) = 0 ( Rhoades[7] )So that {xn} is a Cauchy sequence, hence convergent and {Tx2n},{Sx2n+1} also converge to z. From (xi), ad(Tx2n, Sz, u) + bd(x2n, Tx2n, u) + cd(z, Sz, u)≤ q max{d(x2n, z, u), d(x2n, Tx2n, u), d(z, Sz, u)}In the limiting case, we get ad(z, Sz, u) + cd(z, Sz, u) ≤ qd(z, Sz, u)or, (a + c -q) d(z, Sz, u) ≤ 0.Therefore, Sz = z since a+c > q.Thus z is a fixed point of S. Similarly we can show that z is also a fixed point of T. Hence z is a common fixed point of T and S.The uniqueness of the common fixed point can be easily shown by using (xi). This completes the proof of the theorem. Omitting the term bd(x,Tx,u) and cd(y,Sy,u) from the left hand side of theorem 4.5 we get the following result as a corollary of the above Theorem.Corollary 4.1 Let the self mappings T and S of a complete metric space (X, d) satisfyd(Tx, Sy, u) ≤ q max{d(x, y, u), d(x, Tx, u), d(y, Sy, u)} for x, y, u ε X. Then T and S have a unique common fixed point.5. Discussion and Conclusions
- Our results obtained in 2-metric space with inquality condition involving rational terms have generalized the earlier resuls of Gahler, Rhoades, Iseki etc in terms of inquality condition as well as in terms of a pair of mappings and a family of mappings.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML