1. Introduction

In studying spaces , one of the aims of this study is to introduce spaces that can suit some scientific applications . Many scientific problems in various fields may have their own conditions that might not agree with the geometric structure and properties of some spaces familiar to mathematicians and geometers .

Historically the Euclidean space , then the Cartesian and so on have been serving the scientific needs and the solutions to many problems , but mathematicians always think of new spaces whenever it is crucial to do that , or also they introduce new spaces to be ready for future applications .

In differential geometry , manifolds do their role to meet some scientific demands . This is due to some properties of manifolds , for instance manifolds need not be connected , or closed . They are never countable unless their dimension is zero .

Differentiable manifolds for example lead to Lie groups, and these with their Lie algebras help to introduce some abstract spaces such as symmetric spaces .

When we introduce symmetric spaces , this can be done through different approaches of algebraic and geometric nature .

In this study we are going to discuss some of these approaches which lead to some invariant properties of symmetric spaces . We can look to these spaces from different aspects which unify some algebraic and geometric properties .

2. Preliminaries

2.1. Smooth Manifold

Manifolds are topological spaces that are locally Euclidean and Hausdorff .

A smooth manifold 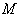is a manifold endowed with a smooth structure , that is an atlas of charts satisfying smoothness conditions .

Simple examples of smooth manifolds are the Euclidean n- space 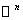and unit sphere .

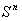2.2. Proposition

A manifold is locally connected , locally compact , a union of a countable collection of compact sets , normal and meterizable .

2.3. A Smooth Tensor Field

Let be a smooth manifold . A smooth tensor field 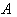on the manifold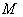of type 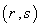is the map 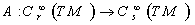, which is multi- linear over 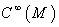, that is , it satisfies the following :

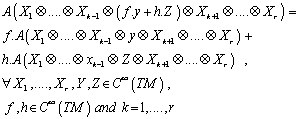Shortly for the smooth tensor field 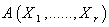, We use the notation

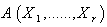. Also 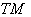denotes the tangent bundle on 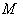, that is the disjoint union of all tangent spaces on .

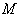2.4. Proposition

Let 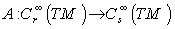be a tensor field of type 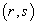and the poin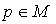t . Let 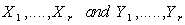be smooth vector fields on 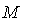such that 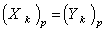for each 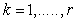, then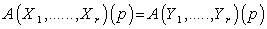

2.5. Definition ( Riemannian Metric )

A Riemannian metric 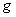on a manifold 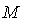is a tensor field

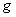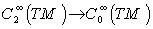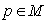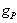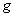
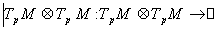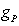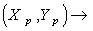
: such that for each the restriction = with : is an inner product on the Tangent space .

2.6. Connections and Riemannian Connections

In a smooth n – manifold 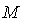with a smooth Riemannian metric 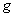, let 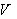be the set of all smooth vector fields on 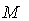. A connection on 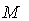is the operator 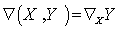, satisfying the conditions :

:

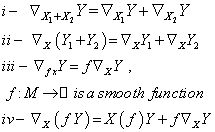If in addition to the above conditions we have

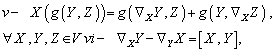then the connection 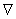is called the Riemannian connection .

We can use for a chart 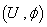on n- manifold : 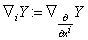, then

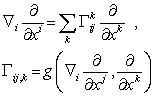(The Chistoffel symbols ) .

If 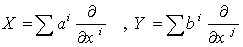, then using 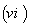above we find the covariant derivative ( or the connection ) :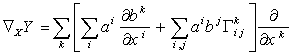

2.7. Parallel Vector Fields & Geodesics

If is a smooth n – manifold with a smooth Riemannian metric .

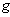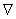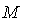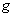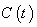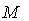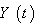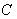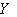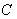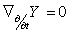Let be the unique Riemannian connection on corresponding to . Let be a smooth regular curve in , be a vector field along . Then is parallel along if and 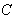is a geodesic in 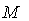if 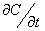is parallel along 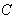, that is , if .

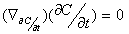2.8. Riemannian Manifold

Let 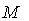be a smooth manifold with a metric 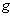, the pair (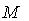, 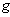) is called a Riemannian manifold . Geometric properties of (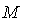, 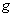) which only depend on the metric 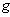are called intrinisic or metric properties .

2.9. Levi – Civita Connection

In a Riemannian manifold with a metric 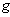, a connection 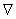is called a Levi – Civita connection if it is torsion- free ( 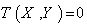) , and is compatible with 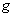, Where :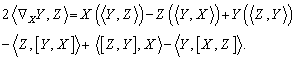

3. Lie groups and Lie algebras

Lie groups and their Lie algebras are very useful and important tools when studying symmetric spaces , this results from the fact that their algebraic properties derive from the group axioms , and their geometric properties derive from the identification of group operation s with points in a topological spaces , and these are manifolds .

We should note that every Lie group is a smooth manifold .

3.1. Definition( Lie group )

A Lie group 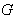is a group satisfying two additional axioms :

(i) The mapping of the group operation 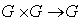defined by 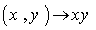, and

(ii) The inverse map 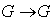defined by 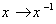, are both smooth .

Examples:

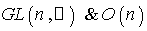are examples of Lie groups .

3.2. Definition ( Lie Algebra of a Lie Group )

The tangent space to a linear Lie group at the identity , denoted g=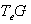is its Lie algebra endowed with a ( non-associative ) multiplication , the Lie bracket satisfying the axioms of a Lie algebra as a vector space .

3.3. Homomorphisms of Lie Groups and Lie Algebras

The homomorphism of the Lie groups 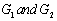is a function 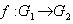which is a homomorphism of groups and a smooth map between the manifolds .

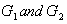If g₁ and g₂ are two Lie algebras , also the homomorphism of Lie algebras is a function 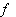: g₁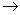 g_{2 which is a linear map between the vector spaces} g₁ and g_{2 preserving Lie brackets ,that is .}

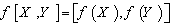3.4. Left and Right Translations

If 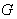is a Lie group , for every 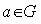we define :

(i ) Left translation as the map 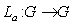such that .

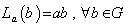(ii ) Right translation as 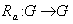such that 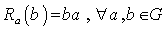. 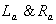are both diffeomorphisms , 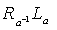or 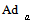_{is given by}

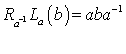The derivative 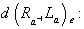g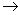g is an isomorphism of Lie algebras , denoted by 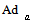: g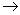g .

That is , .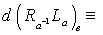

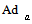3.5. Adjoint Representation

If we denote the Lie group of all bijective linear maps on g by GL(g) , then we call the map 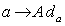where 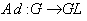( g) the adjoint representation of .

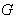g. If 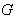is a linear group we have 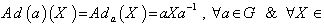The derivative 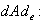g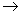 gL(g) denoted by 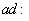g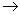gL(g) is called the adjoint representation of g ( where gL(g) denotes the Lie algebra , End(g , g ) of all linear maps on g ) .

In the case of linear group we have 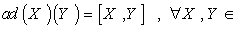g , and

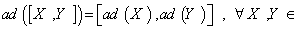g . According to what is mentioned we can define the Lie algebra of the Lie group as :

3.6. Definition ( Lie Bracket )

Given a Lie group 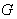, g = 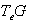with the Lie bracket defined by : 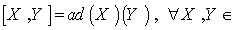g , is the Lie algebra of the Lie group G .

3.7. Left and Right Invariant Vector Fields

Given 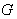is a Lie group , we define a vector field 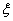on 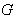as :

(i ) Left-invariant vector field if and only if

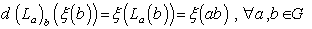, and

(i ) Right – invariant vector field if and only 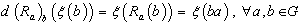if

.

If 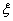is a left – invariant vector field , putting 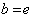, we have :

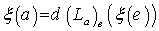, that is 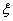is determined by its value 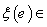g , at the identity .

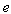The map 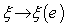, establishes an isomorphism between the space of left – invariant vector fields on 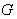and g .

In fact for 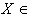g , we define the vector field 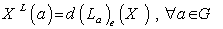, then the map 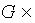g 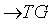given by 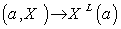is an isomorphism between 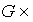g and the tangent bundle .

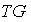3.8. Definition ( Lie Subalgebra and The Ideal )

If g is a Lie algebra , a subalgebra η of g is a subspace of g such that 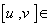η , 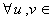η . If η is a subspace of g such that 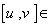η , 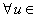η and all 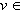g , we call η an ideal in g .

Note that many properties of Lie groups structure can be studied and derived through their Lie algebras , that is why they are important to be studied .

A simple Lie algebra has no proper ideal . The semisimple algebras are constructed of simple ones .

3.9. The Exponential Map

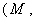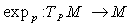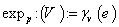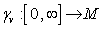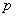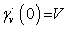In a Riemannian manifold g ) with the point , the exponential map is defined by where is the constant speed geodesic emanating from with and .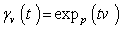

The Lie algebra g generates a group through the exponential mapping . A general group element is 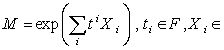g .

If we choose a basis 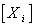for g . Then 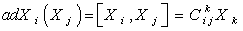, we sum over k . The 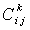are real structure constants .

The structure constants define the matrices 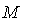of the adjoint representation through .

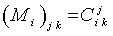3.10. Cartan Subalgebra

In a simple Lie algebra , we have two kinds of generators :

(i) The Cartan subalgebra , which is a maximal abelian subagebra 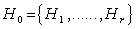such that .

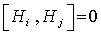On representing each of the Lie algebra by 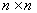matrix , then 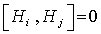means the matrices 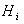can all be diagonalized simultaneously .

Their eigenvalues 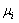are given by 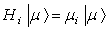, where the eigenvectors are labeled by the weight vectors .

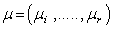(ii) There are raising and lowering operators denoted 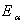such that

.

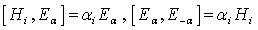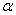is an r – dimensional vector called a root , 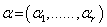and r is the rank of the algebra .

The roots form a lattice in the space dual to the Cartan subalgebra . They are useful in the problem of classification of symmetric spaces .

3.11. Killing Form

If g is a Lie algebra , we define the Killing form 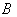of g over afield 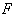as the bilinear form :

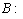g g .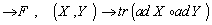

The Lie group and its Lie algebra are called semisimple if the Killing form is nondegenerate .

4. Homogeneous Space

To introduce homogeneous spaces we should remember the action of the group on a set .

4.1. The G-space

A locally compact Hausdorff space equipped with a transitive action of the group 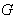, is called a 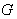- space .

4.2. Theorem

Let 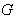be a locally compact group and let 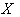be a transitive 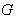- space . Let 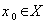and 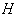be the isotropy group o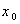f . If 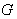is compact , then 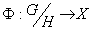given by 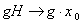is a homomorphism .

4.3. Definition ( Homogeneous Space )

A Homogeneous space 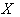is a transitive G- space that is isomorphic to a quotient space 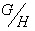. That is , there is an isomorphism by the mapping 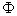as in the previous theorem , making 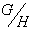isomorphic to .

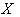In a homogeneous space every point looks exactly like every other point . We can also look at a homogeneous space as a space whose isometry group acts transitively on it .

4.4. Example

As an example of a homogeneous space , the n-sphere 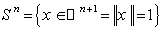, its isometry group is the group of rotations given by 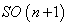. For every two points 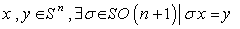, so that there is a transitive action and 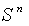is a homogeneous space .

5. Symmetric Spaces

These are spaces which possess the properties of symmetry and homogeneousness,and they have many applications ,this is because they have mixed algebraic and geometric properties . The beginning for these spaces is that they are spaces with parallel curvature tensor , later they were introduced through different approaches . They have much in common . Any symmetric space has its own special geometry , Euclidean , elliptic and hyperbolic are some of these geometries .

We give some approaches to symmetric spaces using some algebraic and geometric properties.

5.1. Some Approaches to Symmetric Spaces

A symmetric space can be considered as :

1 - A Riemannian manifold with point reflection .

2 - A Riemannian manifold with parallel curvature tensor .

3 - A Lie group with certain involution .

4 - A homogeneous space with special isotropy group .

5 - A Riemannian manifold with special holonomy .

6 - A special Killing vector field .

7 - A Lie triple system .

These may be some of many other approaches to symmetric spaces , but we are interested in this work in some of these approaches to reach the required aims of this study .

6. Symmetric Spaces and Parallel Curvature Tensor

The most famous approach to symmetric spaces is that related to Ellie Cartan , we introduce it here to complete the picture of our opinions :

6.1. Definition

A Riemannian manifold 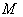is called locally symmetric if its curvature tensor 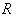is parallel , that is .

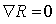6.2. Theorem ( E. Cartan )

Let 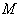be a Riemannian manifold . Then 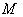is locally symmetric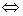 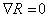, where 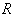is the curvature tensor of 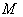, and 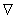is the connection induced on 4-tensor on 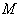by the Levi – Civita connection of .

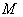6.3. Theorem ( Symmetric Space )

A Complete , Locally symmetric , simply connected Riemannian manifold is a symmetric space .

According to what is mentiond above we can give many examples of symmetric spaces , where we shall give some details on some of them when introducing other approaches to symmetric spaces . Briefly we can say that 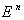( the Euclidean space ) , 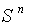( the unit sphere in 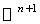) and 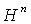( the hyperbolic space ) are all examples of symmetric spaces.

7. Symmetric Spaces with Point Reflection

Here we consider symmetric spaces as Riemannian manifolds with point reflections :

Let 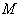be a Riemannian manifold , 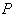a point of 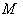. If the geodesic reflection at any point 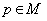is an isometry of 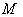, that is 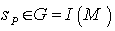, the isometry group of 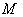, such that

.

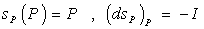The isometry 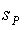is called symmetry at 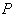. From this definition , 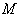is geodesically complete and homogeneous .

We can say that a Symmetric space 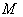is precisely a homogeneous space with a symmetry at some point .

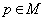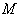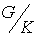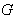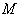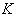We identify the homogeneous space with the coset space where is the isometry group of , and is the isotropy group .

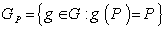7.1. Definition ( Locally Symmetric Space )

A locally symmetric space is a Riemannian manifold in which the geodesic symmetry at each point is an isommetry in a normal neighbourhood of the point . Symmetric Spaces are locally symmetric too, the geodesic symmetries in this case are global isometries .

7.2. Example ( The Unit Sphere )

Let 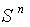be the unit sphere in 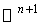with the standard scalar product . On taking the symmetry at any point 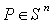as the reflection at the line 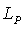in 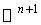, that is 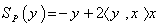. This symmetries generate the full isometry group which is the orthogonal group 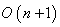. The isotropy group of the last standard unit vector 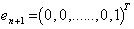is .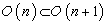

7.3. Example ( The Orthogonal Group ) ( Abstract )

Let 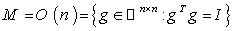, a Submanifold of the matrix space .

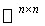The Riemannian metric on 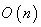is induced from the trace scalar product on :

.

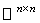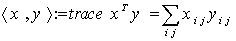For any 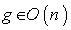and 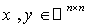we have : ,

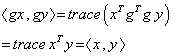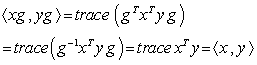( the inner product is preserved ) . Right and left multiplications with 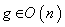preserve the subset 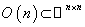, so they act as isometry on 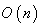turning 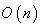into a homogeneous space .

The linear map 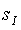on 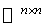given by 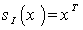is an isometry of 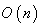preserving 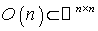and the scalar product of 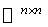. This is the symmetry at the identity matrix 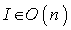since it fixes 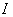and acts as 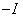on the tangent space 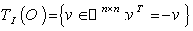. The symmetry at an arbitrary element 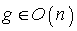is given by 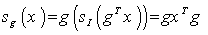, noting that 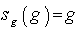and for any 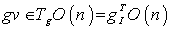, we have .

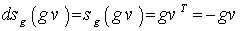8. Symmetric Space as a Lie Group with Involutive Isometry

This approach can be seen through point reflection , then we can introduce the notion of involution and symmetric pairs with involutive automorphism .

8.1. Definition ( Symmetric Space and Involution )

Let 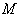be a Riemannian manifold with the metric 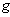such that for every point 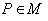there exists an isometry 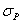of 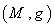called an involution such that :

.

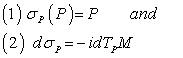Composition of involutions will get translations along geodesics which can be used to extend geodesics to the whole of 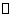and this means 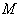is geodesically complete .

8.2. The Role of Lie Groups

Again we consider Lie groups in this approach , this is through the fact that the group of isometries mentioned above is a Lie group .

By Hopf – Rinow theorem any two points in a geodesically complete Riemannian manifold can be connected by a geodesic .

We deduce that the translations along the geodesics make the isometry group 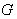( Lie group ) acting on 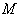transitively . Here also we identify 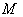with 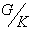( Homogeneous space ) , where 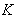is the isotropy group at a point .

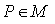9. Characterization of Symmetric Spaces

One of the most surprising features of symmetric spaces is that we can get their properties and information about them from their groups of isometry and this is another scope for more study .

9.1. The Triple ( g , η , ρ )

In the symmetric space 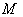, let 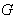be its group of isometry and 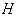is the isotropy group at 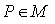then 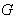has a Lie group structure and 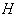is a closed Lie subgroup of 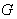. The Lie algebra g of 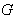is the space of Killing vector fields on 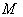. The Lie algebra η of 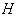is a subalgebra of g and has a natural complementary subspace ρ such that :

g = η 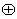ρ , [η, η] η , [η, ρ ] 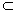ρ and [ρ , ρ ] 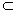ρ .

So the characterization of symmetric spaces is the same as characterization of such triples

( g , η , ρ ) .

10. Results and Conclusions

→ The geometric and algebraic approaches to symmetric spaces can be modified to deduce each other .

→ Most of features of symmetric spaces can be extracted from their Lie algebras or the triple ( g , η , ρ ) .

→ The study of symmetric spaces and continuous research in their properties and classification can lead to most surprising results that can help in their applications .

-The different approaches to symmetric spaces mentioned in this paper , lead to specifying two important features of symmetric spaces , that is homogeneousness and symmetry .

Homogeneousness can be considered as algebraic property through the transitive action of the isometry group while symmetry is a geometric property which can be seen through point reflection in the Riemannian manifold .

An important remark on symmetric spaces is that we can use them in describing some abstract and non- abstract spaces , and this unifies the theory and application of spaces which pave the way for future applications in many fields .