B. R. Sreedhar1, K. Pushpanjali2, G. Y. Sagar3, Y. R. Reddy4
1Department Of Mathematics, Chaitanya Bharathi Institute Of Technology, Hyderabad, 500075, India
2Department Of Statistics, Sri Krishnadevaraya University, Anantapur, 515001, India
3Department Of Mathematics, T R R Engineering College, Hyderabad, 500070, India
4Department Of OR&SQC, Rayalaseema University, Kurnool, 518002, India
Correspondence to: G. Y. Sagar, Department Of Mathematics, T R R Engineering College, Hyderabad, 500070, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper deals with the 3-component identical system under the influence of human errors and Common Cause Shock (CCS) failures. The M L estimates of system availability and frequency of failures were developed in the case of series and parallel systems. Also we developed empirical evidence to establish the validity of the proposed estimates by simulation study.
Keywords:
Availability, Frequency Of Failures, CCS Failures, Human Errors, M L Estimation, Monte-Carlo Simulation
Cite this paper: B. R. Sreedhar, K. Pushpanjali, G. Y. Sagar, Y. R. Reddy, Maximum Likelihood Estimation for Availability Measures of a Three Component Identical System in the Presence of Human Errors and CCS Failures, American Journal of Mathematics and Statistics, Vol. 2 No. 6, 2012, pp. 191-198. doi: 10.5923/j.ajms.20120206.05.
1. Introduction
In most of the studies relating to life testing and reliability, the lifetime is treated as continuous and accordingly continuous probability distributions are proposed as models. David & Epstein[4] have investigated exponential distribution in the life experiments. Interest in estimation is very important for statistical inference of random phenomena and time to failure is treated as random phenomena in reliability theory. There is extensive literature on reliability modeling, inference relating to reliability characteristics. However, there is very little discussion in assessing and estimating system performance measures like availability, frequency of failures etc. Vesely[10] discussed the Binomial failure rate model. Atwood[1], Atwood and Steverson[2] and Meachum and Atwood[7] have applied the Binomial failure rate model for Common cause shock failures to the data associated with nuclear power plants. Chari et al[3] discussed the CCS failures to arrive the expressions for reliability. Lin et al[6] derived the exact maximum likelihood estimates of the parameters included in the lives distribution of components with constant failure rates in a series system. Sarhan and EI-Bassiouny[9] used M L estimation approach to derive the estimators for the parameters included in a parallel system under the assumption that the life times of the system’s components This paper presents, Maximum likelihood estimation approach to assess the performance of the redundant systems. In this connection, we considered three component identical system which is affected by human errors and Common cause shock failures. The M L estimates are proposed for reliability indices such as availability function, frequency of failure function in the case of series and parallel systems. Also the proposed estimates are assessed based on simulated samples.
2. Notations
λi, λc & λh : the failure rates of individual, CCS failures and human errors respectively. p1, p2 & p3: the chance of individual, CCS failures and human errors respectively.µ0, µ1 & µ2: service rates. 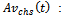 time-dependent system availability for seriesconfiguration in the case of CCS failures as well as human errors.
time-dependent system availability for seriesconfiguration in the case of CCS failures as well as human errors.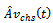 : M L estimate of time-dependent system availability for series configuration in the case of CCS failures as well as human errors.
: M L estimate of time-dependent system availability for series configuration in the case of CCS failures as well as human errors.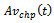 : time-dependent system availability forparallel configuration in the case of CCS failures as well as human errors.
: time-dependent system availability forparallel configuration in the case of CCS failures as well as human errors.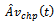 : M L estimate of time-dependent system availability for parallel configuration in the case of CCS failures as well as human errors.
: M L estimate of time-dependent system availability for parallel configuration in the case of CCS failures as well as human errors.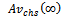 : steady-state system availability for series configuration in the case of CCS failures as well as human errors.
: steady-state system availability for series configuration in the case of CCS failures as well as human errors.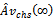 : M L estimate of steady-state system availa-bility for series configuration in the case of CCS failures as well as human errors.
: M L estimate of steady-state system availa-bility for series configuration in the case of CCS failures as well as human errors.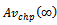 : steady-state system availability for parallel configuration in the case of CCS failures as well as human errors.
: steady-state system availability for parallel configuration in the case of CCS failures as well as human errors.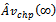 : M L estimate of steady-state system availa-bility for parallel configuration in the case of CCS failures as well as human errors.
: M L estimate of steady-state system availa-bility for parallel configuration in the case of CCS failures as well as human errors.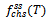 : steady-state frequency of failure for series configuration in the case of CCS failures as well as human errors.
: steady-state frequency of failure for series configuration in the case of CCS failures as well as human errors.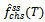 : M L estimate of steady-state frequency of failure for series configuration in the case of CCS failures as well as human errors.
: M L estimate of steady-state frequency of failure for series configuration in the case of CCS failures as well as human errors.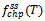 : steady-state frequency of failure for parallel configuration in the case of CCS failures as well as human errors.
: steady-state frequency of failure for parallel configuration in the case of CCS failures as well as human errors.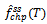 : M L estimate of steady-state frequency of failure for parallel configuration in the case of CCS failures as well as human errors.
: M L estimate of steady-state frequency of failure for parallel configuration in the case of CCS failures as well as human errors.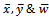 : sample means of the occurrence of individual, CCS failures and human errors respectively.
: sample means of the occurrence of individual, CCS failures and human errors respectively.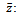 sample mean of service time of the components.
sample mean of service time of the components.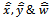 : sample estimates of individual failure rate, CCS failure rate and human errors respectively.
: sample estimates of individual failure rate, CCS failure rate and human errors respectively. 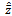 : sample estimate of service time of the components.n: sample size.N: number of simulated samples.M S E: mean square error.
: sample estimate of service time of the components.n: sample size.N: number of simulated samples.M S E: mean square error.
3. Assumptions
(i) The system has three identical components, which are stochastically independent.(ii) The system is affected by individual, CCS failures as well as human errors.(iii) The components in the system will fail singly at the constant rate λi and failure probability is p1(iv) The components may fail due to CCS failures as well as human errors at the constant rates λc and λh with failure probabilities p2 and p3 s.t p1+p2+p3 = 1.(v) The occurrences of all failures follow an exponential distribution.(vi) The failed components are serviced singly and service time follows an exponential distribution with rate of service ‘µ’.
4. The Model
Under the assumptions given in section 3, we have formulated a Markov graph which represents a three component identical system given in Fig.4.1 to derive the availability function and the frequency of encountering the different states in the presence of individual failures, human errors and CCS failures. The numerals in Fig.4.1 denote the state numbers. The quantities appeared in Fig.4.1 are defined as 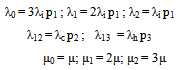 | (1) |
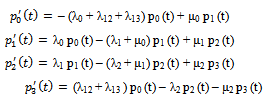 | (2) |
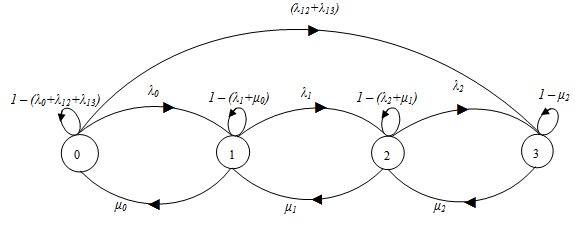 | Figure 4.1. Markov graph for availability and frequency of failure functions of 3-component identical system with individual, CCS failures and human error |
Using the Laplace transformation, the set of equations stated in (2) can be solved with given initial conditions, i.e at t=0, P0 (t) = 1 and P1 (t) = P2 (t) = P3 (t) = 0 and the solution is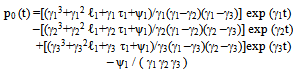 | (3) |
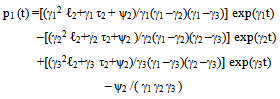 | (4) |
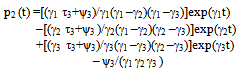 | (5) |
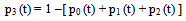 | (6) |
Where the quantities ℓ1, ℓ2, τ1, τ2, τ3, ψ1, ψ2, ψ3, γ1, γ2 & γ3 are defined as follows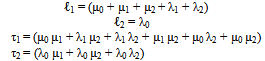 | (7) |
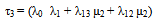 | (8) |
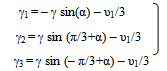 | (10) |
Here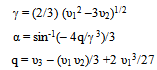 Where υ1, υ2 & υ3 are defined as followsυ1 = (μ0+μ1+μ2+λ0+λ1+λ2+λ12+λ13)υ2 = (μ0 λ2+λ1λ2+λ1μ2+λ0μ1+μ1λ12+λ1λ12+λ12μ2+μ0μ2+λ13 μ2+λ12 λ2+λ1 λ13 + μ0 λ12+μ0 μ1+μ1λ13+λ0 μ2+μ1μ2 + λ0 λ2 + λ0 λ1 + μ0 λ13 + λ13 λ2)υ3 = (λ13 μ0μ1 + λ0λ1λ2 + λ13μ0λ2 + μ2λ1λ13 + λ13μ0λ2+μ0μ1μ2 +λ12μ0μ1+μ0μ2λ12+λ0λ1μ2 + λ12λ1λ2 +μ1μ2λ13+μ2λ1λ12+λ0μ1μ2+μ1μ2λ12+λ13λ1λ2+μ2μ0λ13)And the quantities λ0, λ1, λ2, λ12, λ13, μ0, μ1 & μ2 as given in (1) are to be substitute in equations (7) – (10)
Where υ1, υ2 & υ3 are defined as followsυ1 = (μ0+μ1+μ2+λ0+λ1+λ2+λ12+λ13)υ2 = (μ0 λ2+λ1λ2+λ1μ2+λ0μ1+μ1λ12+λ1λ12+λ12μ2+μ0μ2+λ13 μ2+λ12 λ2+λ1 λ13 + μ0 λ12+μ0 μ1+μ1λ13+λ0 μ2+μ1μ2 + λ0 λ2 + λ0 λ1 + μ0 λ13 + λ13 λ2)υ3 = (λ13 μ0μ1 + λ0λ1λ2 + λ13μ0λ2 + μ2λ1λ13 + λ13μ0λ2+μ0μ1μ2 +λ12μ0μ1+μ0μ2λ12+λ0λ1μ2 + λ12λ1λ2 +μ1μ2λ13+μ2λ1λ12+λ0μ1μ2+μ1μ2λ12+λ13λ1λ2+μ2μ0λ13)And the quantities λ0, λ1, λ2, λ12, λ13, μ0, μ1 & μ2 as given in (1) are to be substitute in equations (7) – (10)
5. Maximum Likelihood (M L) Estimation of the System Availability and Frequency of Failures
This section discusses the maximum likelihood estimation approach for estimating the reliability measures like system availability and frequency of failures of a 3-component identical system under the influence of individual, CCS failures as well as human errors. The M L estimates are proposed for series and parallel systems.Let  be a sample of ‘n’ number of times between individual failures which will obey exponential law. Let
be a sample of ‘n’ number of times between individual failures which will obey exponential law. Let  be a sample of ‘n’ number of times between CCS failures which follow exponential as well.Let
be a sample of ‘n’ number of times between CCS failures which follow exponential as well.Let  be a sample of ‘n’ number of times between human errors failures which follow exponential as well. Let
be a sample of ‘n’ number of times between human errors failures which follow exponential as well. Let 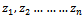 be a sample of ‘n’ number of times repair of the components with exponential population law.
be a sample of ‘n’ number of times repair of the components with exponential population law.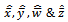 are the maximum likelihood estimates of individual failure rate (λi), CCS failure rate (λc), human errors rate (λh) and repair rate ‘µ’ of the system respectively.Where,
are the maximum likelihood estimates of individual failure rate (λi), CCS failure rate (λc), human errors rate (λh) and repair rate ‘µ’ of the system respectively.Where, 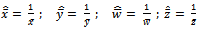 and
and 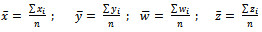 are the sample estimates of the rate of individual failure times, rate of CCS failure times, rate of human error times and rate of repair times of the components respectively.
are the sample estimates of the rate of individual failure times, rate of CCS failure times, rate of human error times and rate of repair times of the components respectively.
5.1. Estimation of Time-dependent System Availability
The M L estimates of time-dependent availability function for series and parallel systems are obtained in this section.
5.1.1. Series System
For a series system, state 1 itself is a absorbing state and hence no transition is allowed from state 1 to state 2 and state 2 to state 3. Hence λ1=λ2=0. Therefore, the time-dependent system availability function for a series system is given by 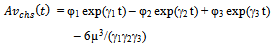 | (11) |
Where φ1 =[ (γ13 + 6μ γ12 + 11μ2 γ1 + 6μ3) / γ1 (γ1 – γ2) (γ1 – γ3) ] φ2 =[ (γ23 + 6μ γ22 + 11μ2 γ2 + 6μ3) / γ2 (γ1 – γ2) (γ2 – γ3) ] φ3 =[ (γ33 + 6μ γ32 + 11μ2 γ3 + 6μ3) / γ3 (γ1 – γ3) (γ2 – γ3) ]and 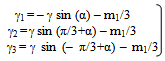 | (12) |
Here = (2/3) (m12 –3 m2)1/2α = sin-1(– 4q/ 3)/3q = m3 – (m1 m2)/3 +2 m13/27Where m1, m2 & m3 are defined as followsm1 = (6μ + 3λi p1 + λc p2 + λh p3)m2 = (15λi p1 μ + 6λc p2 μ +6λh p3 μ +11μ2)m3 = (11λh p3 μ2 + 6μ3 +11λc p2 μ2+18 λi p1 μ2) The expression given in (11) agrees with the result already developed by Sagar et al[8]. Therefore, the maximum likelihood estimate of the time-dependent system availability function of the series system in the presence of individual, CCS failures as well as human errors can be obtained by 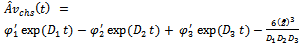 | (13) |
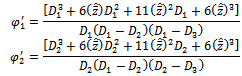 And
And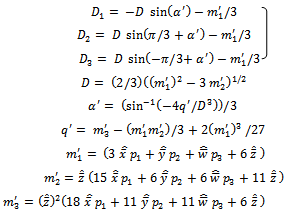 | (14) |
and 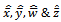 are sample estimates given in “section 5”.
are sample estimates given in “section 5”.
5.1.2. Parallel System
The time-dependent system availability function of theparallel system can be obtained by 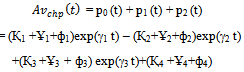 | (15) |
whereҚ1 =[(γ13 + γ12 ℓ1 + τ1 γ1 + ψ1) / γ1 (γ1 – γ2) (γ1 – γ3 )]Қ2 =[(γ23 + γ22 ℓ1 + τ1 γ2 + ψ1) / γ2 (γ1 – γ2) (γ2 – γ3 )] Қ3 =[(γ33 + γ32 ℓ1 + τ1 γ3 + ψ1) / γ3 (γ1 – γ3) (γ2 – γ3 )]Ұ1 =[(γ12 ℓ2 + γ1 τ2 + ψ2) / γ1 (γ1 – γ2) (γ1 – γ3)]Ұ2 =[(γ22 ℓ2 + γ2 τ2 + ψ2) / γ2 (γ1 – γ2) (γ2 – γ3)]Ұ3 =[(γ32 ℓ2 + γ3 τ2 + ψ2) / γ3 (γ1 – γ3) (γ2 – γ3)]ф1 =[(γ1 τ3 + ψ3) / γ1 (γ1 – γ2) (γ1 – γ3)]ф2 =[(γ2 τ3 + ψ3) / γ2 (γ1 – γ2) (γ2 – γ3)]ф3 =[(γ3 τ3 + ψ3) / γ3 (γ1 – γ3) (γ2 – γ3)]Қ4 = – ψ1 / (γ1 γ2 γ3)Ұ4 = – ψ2 / (γ1 γ2 γ3)ф4 = – ψ3 / (γ1 γ2 γ3) The quantities ℓ1, ℓ2, τ1, τ2, τ3, ψ1, ψ2, ψ3, and γ1, γ2, γ3 associated with Қ1, Қ2, Қ3, Қ4, Ұ1, Ұ2, Ұ3, Ұ4, ф1, ф2, ф3, ф4 are defined in (7), (8), (9) & (10) respectively.The time-dependent system availability function given in (15) agrees with the result already developed by Sagar et al[8]. Therefore, the maximum likelihood estimate of the time-dependent system availability function of the parallel system in the presence of individual, CCS failures as well as human errors can be obtained by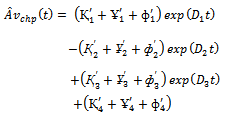 | (16) |
Where 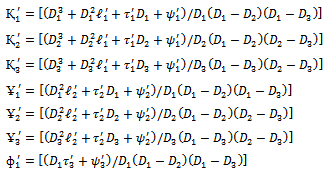
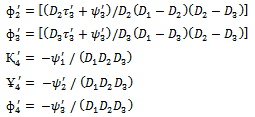 And the quantities
And the quantities 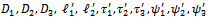 are defined as follows
are defined as follows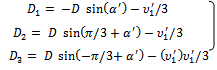 | (17) |
Here 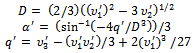 Where
Where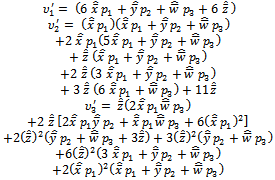 And
And 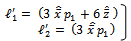 | (18) |
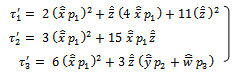 | (19) |
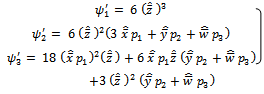 | (20) |
where 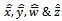 are sample estimates given in “section 5”.
are sample estimates given in “section 5”.
5.2. Estimation of Steady-State System Availability
The maximum likelihood estimates of steady-state system availability functions for series and parallel systems are obtained in this section.
5.2.1. Series System
The steady-state availability of series system can be obtained by using the final value theorem of Laplace transformation.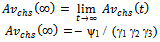 | (21) |
Where ψ1, γ1, γ2 & γ3 are defined in (9) and (12).The above expression given in (21) agrees with the result already developed by Sagar et al[8]. Therefore, the maximum likelihood estimate of steady-state system availability function of series system in the presence of individual, CCS failures as well as human errors can be obtained by 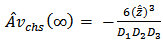 | (22) |
Where 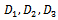 are defined in (14)
are defined in (14)
5.2.2. Parallel System
The steady-state availability function of parallel system can be obtained by using the final value theorem of Laplace transformation.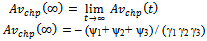 | (23) |
Where ψ1, ψ2, ψ3 and γ1, γ2 , γ3 are defined in (9) and (10)The above expression given in (23) agrees with the result already developed by Sagar et al[8]. Therefore, the maximum likelihood estimate of steady-state system availability function of parallel system in the presence of individual, CCS failures as well as human errors can be obtained by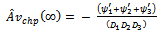 | (24) |
Where 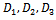 and
and 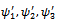 are defined in (17) and (20)
are defined in (17) and (20)
5.3. Estimation of Frequency of Failures
The maximum likelihood estimates of the frequency of failure functions for series and parallel systems in the presence of individual, CCS failures and human errors are obtained in this section.
5.3.1. Series System
The frequency of failure function for series system is given by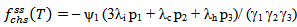 | (25) |
Where ψ1 and 1, 2, 3 are given in (9) and (12)The above expression given in (25) agrees with the result already developed by Sagar et al[8]. Therefore, the M L estimate of the frequency of failure function for series system is given by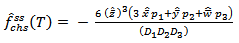 | (26) |
Where 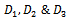 are defined in (14)
are defined in (14)
5.3.2. Parallel System
The frequency of failure function for parallel system is given by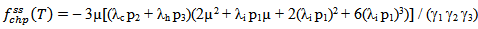 | (27) |
Where 1, 2 &3 are given in (10)The above expression given in (27) agrees with the result already developed by Sagar et al[8]. Therefore, the maximum likelihood estimate of the frequency of failure function of parallel system is given by 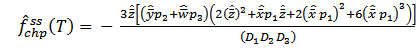 | (28) |
Where 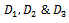 are defined in (17)
are defined in (17)
6. Simulation and Results
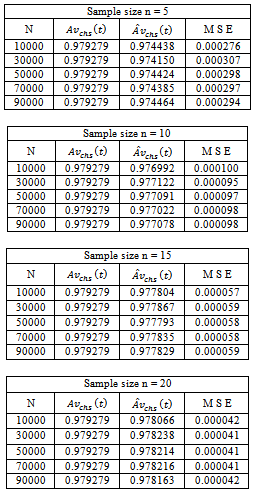
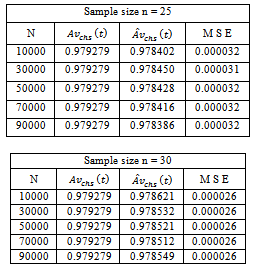
The M L estimates of system availability (time-dependent & steady-state) and frequency of failure functions were not identified with exact or analytical form of probability density function since they are complex functions of the sample information. As such, the probability density function of the estimates is not identified analytically. Hence an attempt is made to establish the validity and to find precision of the estimates of the above measures; Monte-Carlo simulation is used. For a range of specified values of the rates of individual (λi), CCS failures (λc), human errors (λh) and service rate (µ) for the samples of sizes n=5(5)30 were simulated in each case with N=10,000(20,000)90,000 in order to evolve mean square error (MSE) in each case and given in numerical illustration. It is interesting to note that estimation gives a very close estimate in the case of very small samples of size n=5. This shows that M L approach and estimators are quite useful in estimating reliability and availability measures.Table 6.1. Time-dependent system availability function for three component identical Series System with i = 0.05; c = 0.04; h = 0.03; µ = 5; p1 = 0.5; p2 = 0.25; p3 = 0.25; t = 2
 |
| |
|
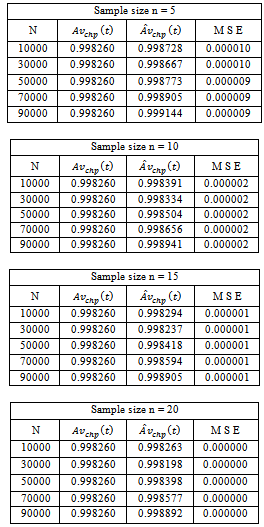
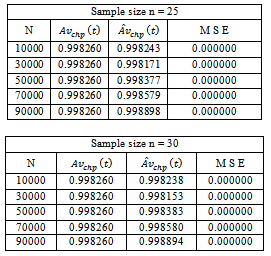
Table 6.2. Time-dependent system availability function for three component identical Parallel System with i = 0.05; c = 0.04; h = 0.03; µ = 5; p1 = 0.5; p2 = 0.25; p3 = 0.25; t = 2
 |
| |
|
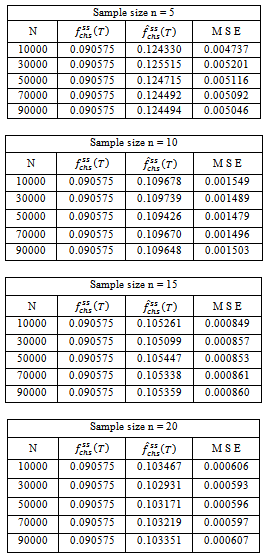
Table 6.3. Frequency of failure function for three component identical Series System with i = 0.05; c = 0.04; h = 0.03; µ = 5; p1 = 0.5; p2 = 0.25; p3 = 0.25
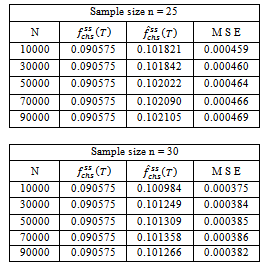 |
| |
|
Table 6.4. Frequency of failure function for three component identical Parallel System with i = 0.05; c = 0.04; h = 0.03; µ = 5; p1 = 0.5; p2 = 0.25; p3 = 0.25
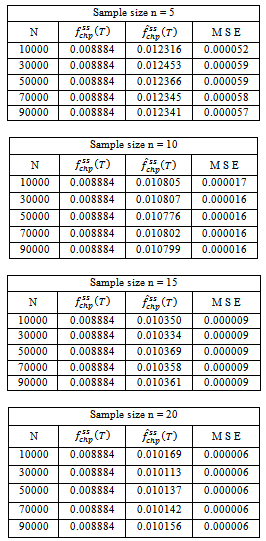
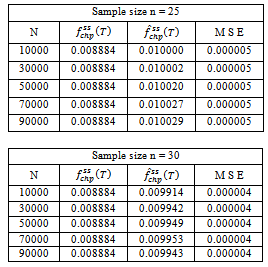 |
| |
|
7. Conclusions
The maximum likelihood estimates of system availability (time-dependent and steady-state) and frequency of failure functions[Av(t), Av(∞), f(T)] were developed for three-component identical system with CCS failures as well as human errors. The estimates are proposed for all the measures said above both for series and parallel systems. We presented numerical simulation studies in order to establish empirically, the validity of the proposed M L estimates of the above measures in the absence of analytical approach. From the simulation results, we observed that(i) The point estimates become more accurate when the sample size is large.(ii) Each of MSE decreases with increasing the sample size.Therefore, this paper suggest that the use of Maximum likelihood estimation approach is found satisfactory for estimation process of some important reliability measures of the system performance, since estimation gives a very close estimate of the above measures even in the case of very small samples of size n=5.
References
| [1] | Atwood, C.L. (1986), The binomial failure rate common cause model in Technometrics, vol: 28, pp. 139-147. |
| [2] | Atwood, C.L. and Steverson (1982), Common cause rates for diesel generators,U.S.Nuclear Regulatory Commission Report NUREG/CR-2099, EGG-EA-5359 (Rev.1) |
| [3] | Chari, A. A., Sastry, M. P and Madhusudhana Verma, S. (1991), “Reliability analysis in the presence of common cause shock failures”, Micro-Electronics and reliability, 31, pp. 15-19. |
| [4] | David and Epstein. Shaping time: Music, the Brain, and Performance. New York: Schirmer Books, 1995. |
| [5] | Dhillon, B.S. and Yang, N. (1992), Stochastic analysis of standby systems with common cause failures and human errors, Microlectronics and Reliability, vol.32, No.12, pp.1699-1712. |
| [6] | Lin, D.K., Usher, J.S. and Guess, F.M. (1993), Exact maximum likelihood estimation using masked system data, IEEE Trans. Reliability, R-42, pp 631-635. |
| [7] | Meachum T. R and Atwood C. L (1983) : Common-cause failure rate for Instrumentation, and control assemblies , U.S regulatory commission report, NURE G/ CR-3289, |
| [8] | Sagar, G. Y., Reddy, Y. R., Umashankar, C and Verma, S. M. (2010),“ Some reliability measures for three component system in the presence of CCS failures and human errors”, Journal of interdisciplinary mathematics, vol.13, No. 2, pp. 143-151. |
| [9] | Sarhan, A.M. and El-Bassiouny, A.H. (2003), Estimation of components reliability in parallel system using masked system life data, Applied Mathematics and Computation, 138/1, pp. 61-75. |
| [10] | Vesely, W.E. (1977), Estimating common cause failure probabilities in reliability and risk analysis: Marshall-Olkin specializations. In Nuclear Systems Reliability Engineering and Risk Assessment, pp.314-341, Society for Industrial and Applied Mathematics, Philadelphia. |

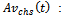 time-dependent system availability for seriesconfiguration in the case of CCS failures as well as human errors.
time-dependent system availability for seriesconfiguration in the case of CCS failures as well as human errors.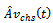 : M L estimate of time-dependent system availability for series configuration in the case of CCS failures as well as human errors.
: M L estimate of time-dependent system availability for series configuration in the case of CCS failures as well as human errors.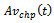 : time-dependent system availability forparallel configuration in the case of CCS failures as well as human errors.
: time-dependent system availability forparallel configuration in the case of CCS failures as well as human errors.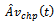 : M L estimate of time-dependent system availability for parallel configuration in the case of CCS failures as well as human errors.
: M L estimate of time-dependent system availability for parallel configuration in the case of CCS failures as well as human errors.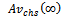 : steady-state system availability for series configuration in the case of CCS failures as well as human errors.
: steady-state system availability for series configuration in the case of CCS failures as well as human errors.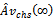 : M L estimate of steady-state system availa-bility for series configuration in the case of CCS failures as well as human errors.
: M L estimate of steady-state system availa-bility for series configuration in the case of CCS failures as well as human errors.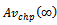 : steady-state system availability for parallel configuration in the case of CCS failures as well as human errors.
: steady-state system availability for parallel configuration in the case of CCS failures as well as human errors.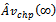 : M L estimate of steady-state system availa-bility for parallel configuration in the case of CCS failures as well as human errors.
: M L estimate of steady-state system availa-bility for parallel configuration in the case of CCS failures as well as human errors.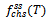 : steady-state frequency of failure for series configuration in the case of CCS failures as well as human errors.
: steady-state frequency of failure for series configuration in the case of CCS failures as well as human errors.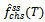 : M L estimate of steady-state frequency of failure for series configuration in the case of CCS failures as well as human errors.
: M L estimate of steady-state frequency of failure for series configuration in the case of CCS failures as well as human errors.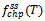 : steady-state frequency of failure for parallel configuration in the case of CCS failures as well as human errors.
: steady-state frequency of failure for parallel configuration in the case of CCS failures as well as human errors.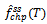 : M L estimate of steady-state frequency of failure for parallel configuration in the case of CCS failures as well as human errors.
: M L estimate of steady-state frequency of failure for parallel configuration in the case of CCS failures as well as human errors.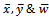 : sample means of the occurrence of individual, CCS failures and human errors respectively.
: sample means of the occurrence of individual, CCS failures and human errors respectively.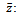 sample mean of service time of the components.
sample mean of service time of the components.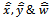 : sample estimates of individual failure rate, CCS failure rate and human errors respectively.
: sample estimates of individual failure rate, CCS failure rate and human errors respectively. 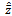 : sample estimate of service time of the components.n: sample size.N: number of simulated samples.M S E: mean square error.
: sample estimate of service time of the components.n: sample size.N: number of simulated samples.M S E: mean square error.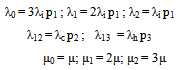
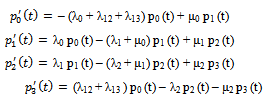

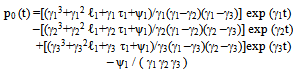
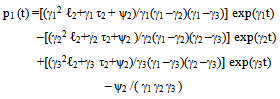
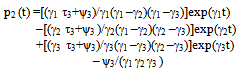
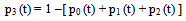
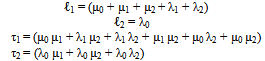
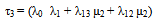
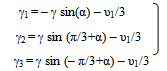
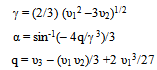 Where υ1, υ2 & υ3 are defined as followsυ1 = (μ0+μ1+μ2+λ0+λ1+λ2+λ12+λ13)υ2 = (μ0 λ2+λ1λ2+λ1μ2+λ0μ1+μ1λ12+λ1λ12+λ12μ2+μ0μ2+λ13 μ2+λ12 λ2+λ1 λ13 + μ0 λ12+μ0 μ1+μ1λ13+λ0 μ2+μ1μ2 + λ0 λ2 + λ0 λ1 + μ0 λ13 + λ13 λ2)υ3 = (λ13 μ0μ1 + λ0λ1λ2 + λ13μ0λ2 + μ2λ1λ13 + λ13μ0λ2+μ0μ1μ2 +λ12μ0μ1+μ0μ2λ12+λ0λ1μ2 + λ12λ1λ2 +μ1μ2λ13+μ2λ1λ12+λ0μ1μ2+μ1μ2λ12+λ13λ1λ2+μ2μ0λ13)And the quantities λ0, λ1, λ2, λ12, λ13, μ0, μ1 & μ2 as given in (1) are to be substitute in equations (7) – (10)
Where υ1, υ2 & υ3 are defined as followsυ1 = (μ0+μ1+μ2+λ0+λ1+λ2+λ12+λ13)υ2 = (μ0 λ2+λ1λ2+λ1μ2+λ0μ1+μ1λ12+λ1λ12+λ12μ2+μ0μ2+λ13 μ2+λ12 λ2+λ1 λ13 + μ0 λ12+μ0 μ1+μ1λ13+λ0 μ2+μ1μ2 + λ0 λ2 + λ0 λ1 + μ0 λ13 + λ13 λ2)υ3 = (λ13 μ0μ1 + λ0λ1λ2 + λ13μ0λ2 + μ2λ1λ13 + λ13μ0λ2+μ0μ1μ2 +λ12μ0μ1+μ0μ2λ12+λ0λ1μ2 + λ12λ1λ2 +μ1μ2λ13+μ2λ1λ12+λ0μ1μ2+μ1μ2λ12+λ13λ1λ2+μ2μ0λ13)And the quantities λ0, λ1, λ2, λ12, λ13, μ0, μ1 & μ2 as given in (1) are to be substitute in equations (7) – (10) be a sample of ‘n’ number of times between individual failures which will obey exponential law. Let
be a sample of ‘n’ number of times between individual failures which will obey exponential law. Let 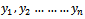 be a sample of ‘n’ number of times between CCS failures which follow exponential as well.Let
be a sample of ‘n’ number of times between CCS failures which follow exponential as well.Let  be a sample of ‘n’ number of times between human errors failures which follow exponential as well. Let
be a sample of ‘n’ number of times between human errors failures which follow exponential as well. Let  be a sample of ‘n’ number of times repair of the components with exponential population law.
be a sample of ‘n’ number of times repair of the components with exponential population law. are the maximum likelihood estimates of individual failure rate (λi), CCS failure rate (λc), human errors rate (λh) and repair rate ‘µ’ of the system respectively.Where,
are the maximum likelihood estimates of individual failure rate (λi), CCS failure rate (λc), human errors rate (λh) and repair rate ‘µ’ of the system respectively.Where, 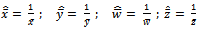 and
and 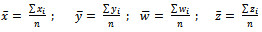 are the sample estimates of the rate of individual failure times, rate of CCS failure times, rate of human error times and rate of repair times of the components respectively.
are the sample estimates of the rate of individual failure times, rate of CCS failure times, rate of human error times and rate of repair times of the components respectively.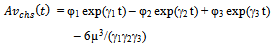
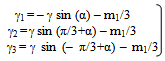
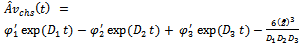
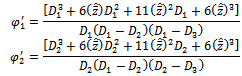 And
And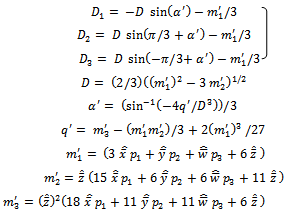
 are sample estimates given in “section 5”.
are sample estimates given in “section 5”.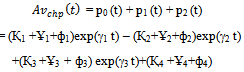
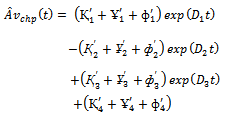
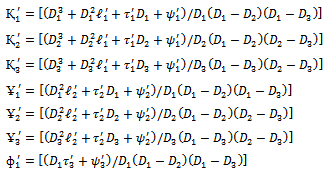
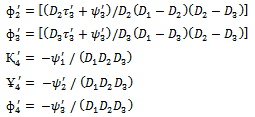 And the quantities
And the quantities 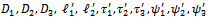 are defined as follows
are defined as follows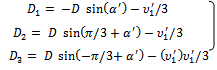
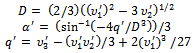 Where
Where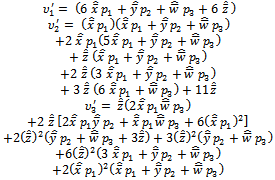 And
And 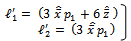
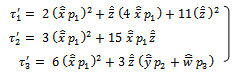
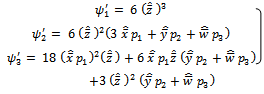
 are sample estimates given in “section 5”.
are sample estimates given in “section 5”.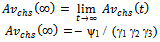
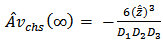
 are defined in (14)
are defined in (14)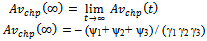
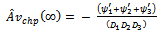
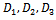 and
and 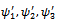 are defined in (17) and (20)
are defined in (17) and (20)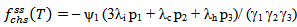
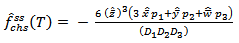
 are defined in (14)
are defined in (14)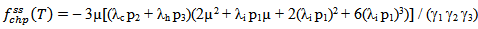
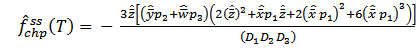
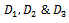 are defined in (17)
are defined in (17) Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML






