Dhwyia S. Hassan 1, Faten F. Albadri 2, Nathier A. Ibrahim 3, Hani Aziz Ameen 4
1Head Department of Industrial Management, College of Administration & Economic, Baghdad University, Iraq
2Department of Statistics, College of Administration & Economic, Baghdad University, Iraq
3Department of Banks Economics, College of Business Economics, Al-Nahrain University, Iraq
4Dies and Tools Eng. Dept. , Technical College Baghdad – Iraq
Correspondence to: Hani Aziz Ameen , Dies and Tools Eng. Dept. , Technical College Baghdad – Iraq.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, the probability distribution (Generalized Rayleigh) with two parameters 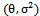 , in case of outlier, is developed, where the probability density function (
, in case of outlier, is developed, where the probability density function (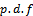 ) is defined, and its moment generating function is derived, to help us in finding the moments, also its cumulative distribution function is found to be used, in obtaining the least squares estimator of the parameters
) is defined, and its moment generating function is derived, to help us in finding the moments, also its cumulative distribution function is found to be used, in obtaining the least squares estimator of the parameters 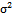 and
and  . The parameters are estimated also by method of moments and method of least square, and also mixture of the estimators are derived, and explained, the estimators of maximum likelihood for
. The parameters are estimated also by method of moments and method of least square, and also mixture of the estimators are derived, and explained, the estimators of maximum likelihood for 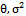 are also obtained.
are also obtained.
Keywords:
Generalized two Parameter Rayleigh Distribution, Uniform Distribution Outlier, MLE, Moments and Least Square and Mixture Estimators
Cite this paper:
Dhwyia S. Hassan , Faten F. Albadri , Nathier A. Ibrahim , Hani Aziz Ameen , "Proposed Methods for Estimating Parameters of the Generalized Raylieh Distribution in the Presence of One Outlier", American Journal of Mathematics and Statistics, Vol. 2 No. 6, 2012, pp. 178-183. doi: 10.5923/j.ajms.20120206.03.
1. Introduction
The probability Rayleigh distribution naturally arises in cases when the wind speed data is analysis into two-orthogonal dimensional vector components, where the magnitude of components is independent and normally distributed with equal variances. Also this distribution arises in the case of random complex numbers whose real and imaginary components are 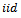 as normal.The two parameters parameters, Burr Type
as normal.The two parameters parameters, Burr Type 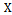 , which introduced by[7], is called Generalized Rayleigh distribution. In this paper, we introduce a new two-parameter Generalized Rayleigh in presence of one outlier generated from another distribution, after definition of proposed distribution, its Moment-Generating function is derived, to help us in finding the first and second moments for this distribution, these moments are used to obtain the mixture estimator of parameters, as well as the Maximum Likelihood estimators. The paper is organized as follows: In section (2) we present the
, which introduced by[7], is called Generalized Rayleigh distribution. In this paper, we introduce a new two-parameter Generalized Rayleigh in presence of one outlier generated from another distribution, after definition of proposed distribution, its Moment-Generating function is derived, to help us in finding the first and second moments for this distribution, these moments are used to obtain the mixture estimator of parameters, as well as the Maximum Likelihood estimators. The paper is organized as follows: In section (2) we present the 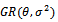 and its properties, and the provides its
and its properties, and the provides its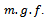 Then section (3), discuss finding moment generting function and the methods of estimating parameters which are Maximum Likelihood and Least Squares and Mixture of estimators are derived. These estimators are compared using (MSE), through simulation programs, prepared for this purpose.In this paper, we introduce a new family of continues distribution, called a new – two parameter generalized Rayleigh GR
Then section (3), discuss finding moment generting function and the methods of estimating parameters which are Maximum Likelihood and Least Squares and Mixture of estimators are derived. These estimators are compared using (MSE), through simulation programs, prepared for this purpose.In this paper, we introduce a new family of continues distribution, called a new – two parameter generalized Rayleigh GR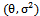 in presence of outlier generated distribution from another distribution i.e the distribution depend on mixing the distribution of
in presence of outlier generated distribution from another distribution i.e the distribution depend on mixing the distribution of  random variables, distributed as Rayleigh with scale parameter
random variables, distributed as Rayleigh with scale parameter 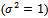 , and shape parameter
, and shape parameter 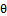 while the
while the 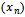 random variable which represents the outlier is one random variable that is uniformly distributed
random variable which represents the outlier is one random variable that is uniformly distributed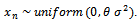 So the aim of research is how to find the marginal
So the aim of research is how to find the marginal 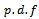 of this type of distribution, in precence of outlier, and also how to derive its cumulative distribution function, and it's moment generating function to help in obtaining the moments after all required derivation three methods are introduced include moment estimators and least squares estimators, and maximum likelihood estimators.
of this type of distribution, in precence of outlier, and also how to derive its cumulative distribution function, and it's moment generating function to help in obtaining the moments after all required derivation three methods are introduced include moment estimators and least squares estimators, and maximum likelihood estimators.
2. Definition of Distribution
Let the random variables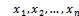 are such that
are such that 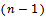 of them are distributed as Rayleigh with scale parameter
of them are distributed as Rayleigh with scale parameter 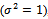 , and shape parameter (
, and shape parameter ( ), i.e.
), i.e.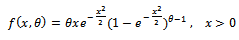 | (1) |
With cumulative 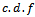 is:
is: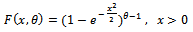 | (2) |
The random variables 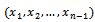 have the
have the 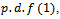 and one random variable
and one random variable 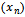 is distributed with
is distributed with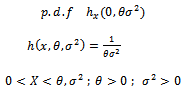 | (3) |
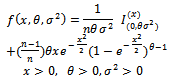 | (4) |
And cumulative distribution function is: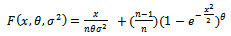 | (5) |
3. Moment Generating Function
The 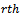 moments of
moments of 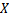 may be determined direct or using Moment generating function technique. Now we derive
may be determined direct or using Moment generating function technique. Now we derive 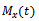 for the distribution defined in (1):
for the distribution defined in (1):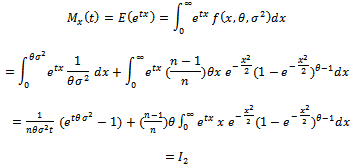 | (6) |
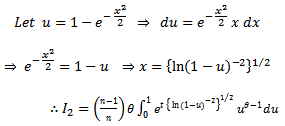 | (7) |
after simplification of (7), it can be written as: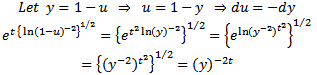 Therefore equation (7) can be written as (8):
Therefore equation (7) can be written as (8):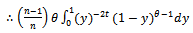 | (8) |
According to Beta formula: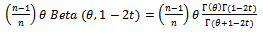 | (9) |
Therefore 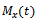 :
: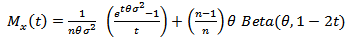 | (10) |
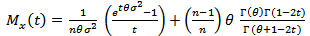 | (11) |
Differentiating 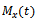 and evaluating at
and evaluating at 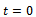 we get
we get  and
and 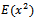 as:
as: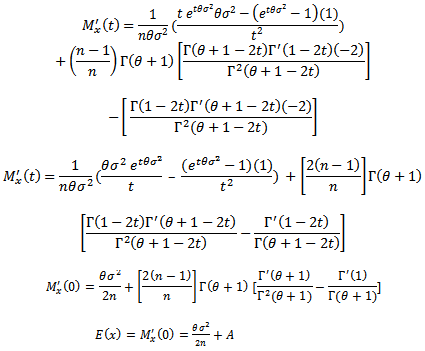 | (12) |
Taking the second derivative 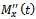 , we have
, we have 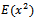 as:
as: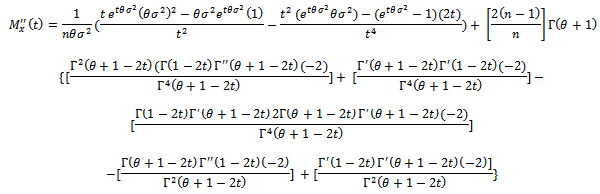 Then:
Then: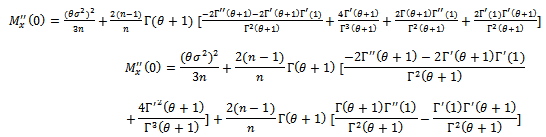 Then:
Then: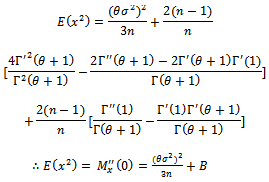 | (13) |
Where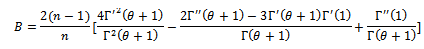 Therefore:
Therefore: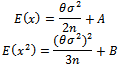 where A, B are functions of
where A, B are functions of 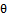 , the Moment estimator's of
, the Moment estimator's of 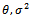 are obtained as follows:
are obtained as follows: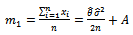
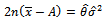 | (14) |
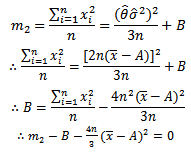 | (15) |
To estimate 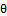 we can solve (15) by Newton Raphson method. Hence the solution of equation (15) is:
we can solve (15) by Newton Raphson method. Hence the solution of equation (15) is: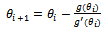 | (16) |
Where: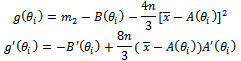 To estimate
To estimate 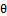 we can solve equation (3) by Newton Raphson method.
we can solve equation (3) by Newton Raphson method.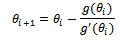 Since:
Since: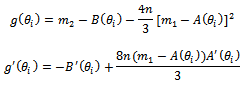 Where:
Where: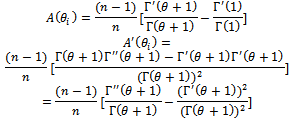 If
If 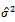 known then:
known then: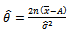 | (17) |
This value can be considered as initial value for solving equation (16) by Newton Raphson method.Also to proceed in finding the moment estimator for the parameter 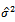 , the following equation is applied as follows:
, the following equation is applied as follows: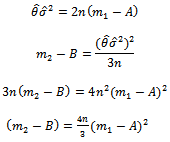 | (18) |
Also the estimate 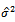 can be obtained by solving equation (18) by Newton Raphson method:
can be obtained by solving equation (18) by Newton Raphson method: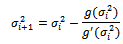 where;
where;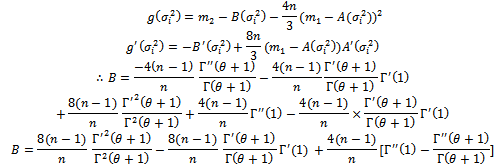
4. Leat Squares Estimators
In this section we provide the regression based method estimators of unknown parameters, which was originally suggested by[16] to estimate the parameters of Beta distribution.Suppose 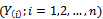 denotes the ordered sample, where:
denotes the ordered sample, where: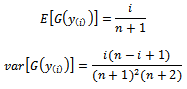 The
The 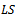 estimators for the unknown parameters
estimators for the unknown parameters 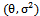 of the proposed
of the proposed 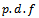 of Generalized Rayleigh with two parameters
of Generalized Rayleigh with two parameters 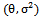 in case of outlier (i.e equation 3), and its
in case of outlier (i.e equation 3), and its 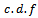 (equation 5), can be obtained by minimizing the quantity T, defined in equation (19):
(equation 5), can be obtained by minimizing the quantity T, defined in equation (19):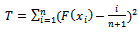 | (19) |
with respect to 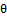 and
and 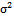 :
: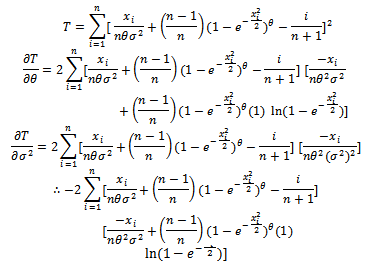 | (20) |
Also we find 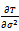 :
: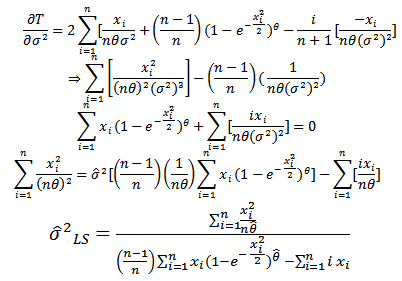 | (21) |
Where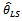 is estimated from equation (20) which is non linear equation can be solved using Newton Raphson method, or we can use Moment estimator of
is estimated from equation (20) which is non linear equation can be solved using Newton Raphson method, or we can use Moment estimator of 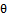 (equation 17) to obtain least square estimator of parameter (
(equation 17) to obtain least square estimator of parameter (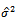 ), and then obtain the mixed estimator.
), and then obtain the mixed estimator.
5. Maximum Likelihood Estimators
Let the random variables 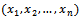 are such that
are such that 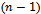 of them are distributed with
of them are distributed with  and one variable is distributed with
and one variable is distributed with 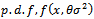 , so the joint distribution of
, so the joint distribution of 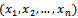 are:
are: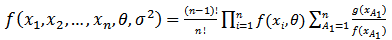 | (21) |
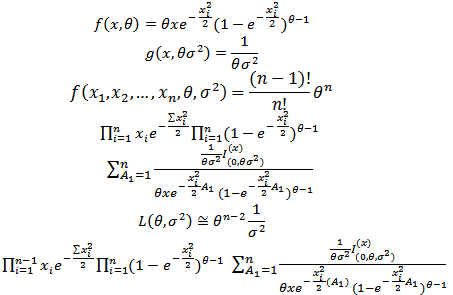 | (22) |
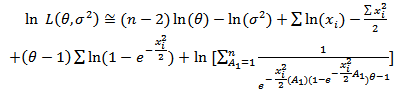 | (23) |
Where 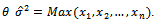
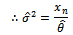
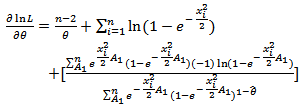 | (24) |
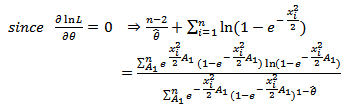 | (25) |
Non linear equation (25) can be solved by using Newton Raphson method: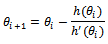 to obtai
to obtai 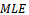 for
for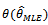 .Summary1. The
.Summary1. The 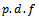 of
of 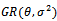 in presence of outlier is defined in equation (1).2. The
in presence of outlier is defined in equation (1).2. The 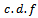 is obtained in closed from equation (5).3. The Moment Generating function is derived and written in a closed from equation (10).4. First and second Moments of this distribution are obtained equation (12) and equation (13).5. Moment's estimator's can be obtained from equation (14) and (15) using Newton Raphson formula (16) and (18).6. Since the
is obtained in closed from equation (5).3. The Moment Generating function is derived and written in a closed from equation (10).4. First and second Moments of this distribution are obtained equation (12) and equation (13).5. Moment's estimator's can be obtained from equation (14) and (15) using Newton Raphson formula (16) and (18).6. Since the 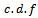 was found in closed from equation (5), it can be used to find the LS estimator, through minimizing equation (19), the estimators of LS are obtained from equations (20, 21).7. The Likelihood function is defined in equations (21), (22) and (23), and then the Maximum Likelihood estimator's are explained in equations (24) and (25).8. Any estimators of Moments, LS can be used in MLE to obtain the Mixture estimators.
was found in closed from equation (5), it can be used to find the LS estimator, through minimizing equation (19), the estimators of LS are obtained from equations (20, 21).7. The Likelihood function is defined in equations (21), (22) and (23), and then the Maximum Likelihood estimator's are explained in equations (24) and (25).8. Any estimators of Moments, LS can be used in MLE to obtain the Mixture estimators.
6. Conclusions
This paper offers a new family of distributions, the two - parameter Rayleigh distribution in the presence of one outlier, which is important for analysis lifetime data. The distribution has two parameters (scale parameter 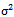 , and shape parameter
, and shape parameter 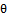 ), and consist of mixing the distribution of
), and consist of mixing the distribution of 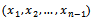 random variables with the distribution of random variable (
random variables with the distribution of random variable (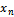 ), i.e (the distribution of
), i.e (the distribution of 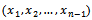 is Rayleigh distribution with (
is Rayleigh distribution with (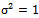 ) and
) and 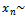 uniformly with
uniformly with 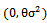 , and the replicate each experiment (R=1000), and to use mean square error (MSE) or integrated mean square error (IMSE) for comparison. We have studied various method for estimating the parameters, (Least Squares, Moments, Mixture), and derived the Moment Generating function, which is used to obtain the first and second Moment of this
, and the replicate each experiment (R=1000), and to use mean square error (MSE) or integrated mean square error (IMSE) for comparison. We have studied various method for estimating the parameters, (Least Squares, Moments, Mixture), and derived the Moment Generating function, which is used to obtain the first and second Moment of this 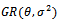 , and then used as a possible alternative method for estimating Parameters.This work will be done in another suggestion in future, to apply this method on another distribution.
, and then used as a possible alternative method for estimating Parameters.This work will be done in another suggestion in future, to apply this method on another distribution.
References
| [1] | Aslam, M., (2008). "Economic reliability acceptance sampling plan for generalized Rayleigh distribution", Journal of Statistics, 15(1), 26-35. |
| [2] | Aslam, M., C.-H. Jun, Y.L. Lio, and M. Ahmad, ( 2011) “Group acceptance sampling plans for the generalized Rayleigh distribution”, International Journal of Intelligent Technologies & Applied Statistics, 4(3), 355-365, September 2011. |
| [3] | A. Soliman, Essam A. Amin, and Alaa A. Abd-El Aziz,(2010) ," Estimation and Prediction from Inverse Rayleigh Distribution Based on Lower Record Values", Applied Mathematical Sciences, Vol. 4, 2010, no. 62, 3057 – 3066. |
| [4] | Hryniewicz, Q., (2008)," Statistics with fuzzy data in statistical quality control", Soft Company. 12:229 – 234. |
| [5] | Kishore K. Das and Tanusree Deb Roy, (2011)," Applicability of Length Biased Weighted Generalized Rayleigh Distribution" Pelagia Research Library Advances in Applied Science Research, 2011, 2 (4):320-327 . |
| [6] | Mohamed Saber Fallah, Seyed Taghi Akhavan, and Mohamed Hossein Abooie, (2011) " A new Acceptance sampling plan based on cumulative sums of conforming Run – Lengths, " Journal of Industrial and systems engineering. Vol.4.No.4, pp256 – 265. |
| [7] | Muhammad Aslam, (2008)," Economic Reliability Acceptance Sampling Plan for Generalized Rayleigh Distribution" ISSN 1684-8403 Journal of Statistics Volume 15, 2008, pp. 26-35. |
| [8] | Muhammad Aslam1, Chi-Hyuck Jun, Y. L. Lio and Munir Ahmad,(2011)," Group Acceptance Sampling Plans for the Generalized Rayleigh Distribution" International Journal of Intelligent Technologies and Applied Statistics Vol.4, No.3 (2011) pp.355-365. |
| [9] | Raqab, M. Z. (1998); "Order Statistics from the Burr Type X Mode"; Computer Mathematics and Applications, Vol. 36, 111-120. |
| [10] | Raqab, M. Z. and Kundu, D. (2006); "Burr Type X Distribution: Revisited"; Journal of Probability and Statistical Science, Vol. 4, 179-193. |
| [11] | Saima Altaf, and Muhamed Aslam, (2011), " Bayesian analysis of the Davidson model for paired comparision with order effect using non informative priors", Pak. J. Stats. Vol. 27(2), 171 – 185. |
| [12] | Sanka Dey, (2008), " Minimax estimation of the parameter of the Rayliegh distribution under quadratic loss function", Data Science Journal, Vol. 7,23. |
| [13] | Surles, J. G. and Padgett, W. J. (1998); " inference for in the Burr type X model", Journal of applied statistical sciences, 7, 225-238. |
| [14] | Surles, J. G. and Padgett, W. J. (2001); "inference For Reliability and Stress-Strength For a Scaled Burr Type X Distribution"; Lifetime Data Analysis, Vol. 7, 187-200. |
| [15] | Surles, J. G. and Padgett, W. J. (2005); "Some Properties of a Scaled Burr Type X Distribution"; Journal of Statistical Planning and Inference, Vol. 128, 271-280. |
| [16] | Swain, J.J., Venkatraman S., Wilson, J.R. (1988), "Distribution Selection and Validation", Journal of Statistical Computation and Simulation, Vol. 29, pp. 271-297. |
| [17] | Tang, K. (1988)," Economic design of product specifications for a complete inspection plan", International Journal of production research, Vol. 26. No. 2, 203 – 219. |

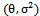 , in case of outlier, is developed, where the probability density function (
, in case of outlier, is developed, where the probability density function (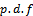 ) is defined, and its moment generating function is derived, to help us in finding the moments, also its cumulative distribution function is found to be used, in obtaining the least squares estimator of the parameters
) is defined, and its moment generating function is derived, to help us in finding the moments, also its cumulative distribution function is found to be used, in obtaining the least squares estimator of the parameters 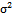 and
and  . The parameters are estimated also by method of moments and method of least square, and also mixture of the estimators are derived, and explained, the estimators of maximum likelihood for
. The parameters are estimated also by method of moments and method of least square, and also mixture of the estimators are derived, and explained, the estimators of maximum likelihood for 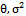 are also obtained.
are also obtained.
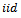 as normal.The two parameters parameters, Burr Type
as normal.The two parameters parameters, Burr Type 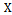 , which introduced by[7], is called Generalized Rayleigh distribution. In this paper, we introduce a new two-parameter Generalized Rayleigh in presence of one outlier generated from another distribution, after definition of proposed distribution, its Moment-Generating function is derived, to help us in finding the first and second moments for this distribution, these moments are used to obtain the mixture estimator of parameters, as well as the Maximum Likelihood estimators. The paper is organized as follows: In section (2) we present the
, which introduced by[7], is called Generalized Rayleigh distribution. In this paper, we introduce a new two-parameter Generalized Rayleigh in presence of one outlier generated from another distribution, after definition of proposed distribution, its Moment-Generating function is derived, to help us in finding the first and second moments for this distribution, these moments are used to obtain the mixture estimator of parameters, as well as the Maximum Likelihood estimators. The paper is organized as follows: In section (2) we present the 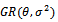 and its properties, and the provides its
and its properties, and the provides its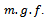 Then section (3), discuss finding moment generting function and the methods of estimating parameters which are Maximum Likelihood and Least Squares and Mixture of estimators are derived. These estimators are compared using (MSE), through simulation programs, prepared for this purpose.In this paper, we introduce a new family of continues distribution, called a new – two parameter generalized Rayleigh GR
Then section (3), discuss finding moment generting function and the methods of estimating parameters which are Maximum Likelihood and Least Squares and Mixture of estimators are derived. These estimators are compared using (MSE), through simulation programs, prepared for this purpose.In this paper, we introduce a new family of continues distribution, called a new – two parameter generalized Rayleigh GR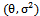 in presence of outlier generated distribution from another distribution i.e the distribution depend on mixing the distribution of
in presence of outlier generated distribution from another distribution i.e the distribution depend on mixing the distribution of  random variables, distributed as Rayleigh with scale parameter
random variables, distributed as Rayleigh with scale parameter 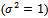 , and shape parameter
, and shape parameter 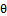 while the
while the 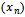 random variable which represents the outlier is one random variable that is uniformly distributed
random variable which represents the outlier is one random variable that is uniformly distributed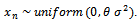 So the aim of research is how to find the marginal
So the aim of research is how to find the marginal 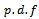 of this type of distribution, in precence of outlier, and also how to derive its cumulative distribution function, and it's moment generating function to help in obtaining the moments after all required derivation three methods are introduced include moment estimators and least squares estimators, and maximum likelihood estimators.
of this type of distribution, in precence of outlier, and also how to derive its cumulative distribution function, and it's moment generating function to help in obtaining the moments after all required derivation three methods are introduced include moment estimators and least squares estimators, and maximum likelihood estimators.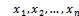 are such that
are such that 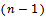 of them are distributed as Rayleigh with scale parameter
of them are distributed as Rayleigh with scale parameter 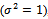 , and shape parameter (
, and shape parameter ( ), i.e.
), i.e.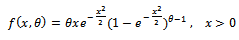
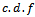 is:
is: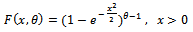
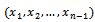 have the
have the 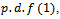 and one random variable
and one random variable 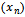 is distributed with
is distributed with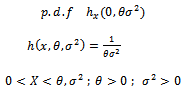
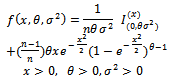
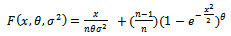
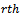 moments of
moments of 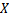 may be determined direct or using Moment generating function technique. Now we derive
may be determined direct or using Moment generating function technique. Now we derive 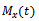 for the distribution defined in (1):
for the distribution defined in (1):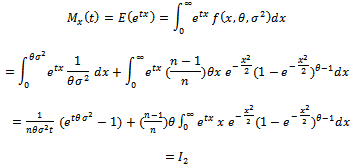
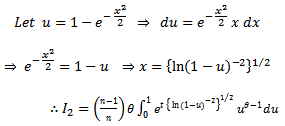
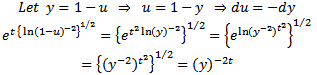 Therefore equation (7) can be written as (8):
Therefore equation (7) can be written as (8):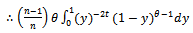
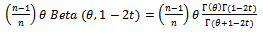
 :
: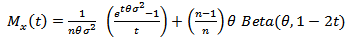
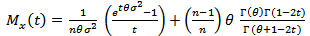
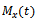 and evaluating at
and evaluating at 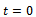 we get
we get 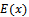 and
and 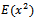 as:
as: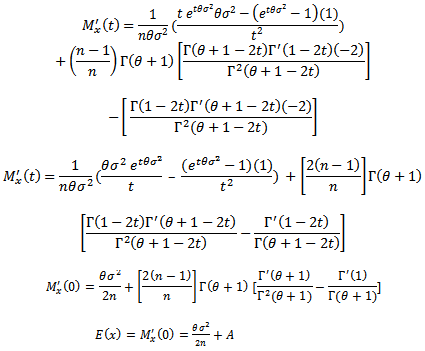
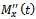 , we have
, we have 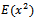 as:
as: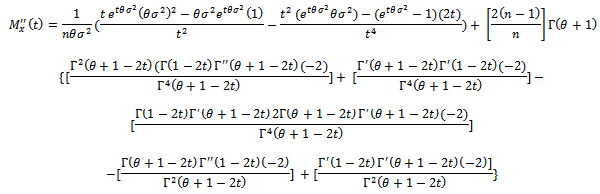 Then:
Then: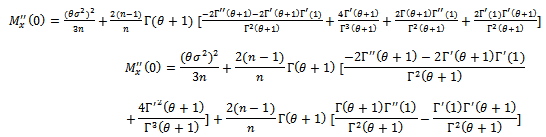 Then:
Then: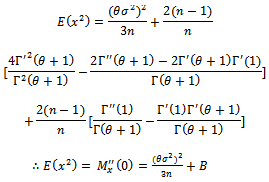
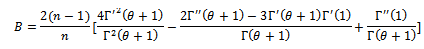 Therefore:
Therefore: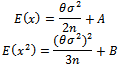 where A, B are functions of
where A, B are functions of 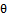 , the Moment estimator's of
, the Moment estimator's of 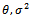 are obtained as follows:
are obtained as follows: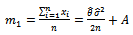
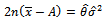
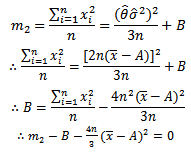
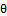 we can solve (15) by Newton Raphson method. Hence the solution of equation (15) is:
we can solve (15) by Newton Raphson method. Hence the solution of equation (15) is: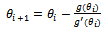
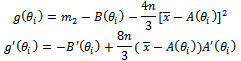 To estimate
To estimate 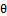 we can solve equation (3) by Newton Raphson method.
we can solve equation (3) by Newton Raphson method.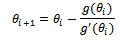 Since:
Since: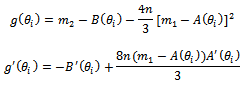 Where:
Where: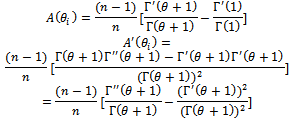 If
If 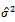 known then:
known then: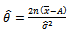
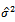 , the following equation is applied as follows:
, the following equation is applied as follows: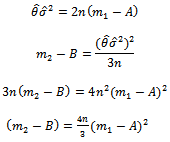
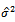 can be obtained by solving equation (18) by Newton Raphson method:
can be obtained by solving equation (18) by Newton Raphson method: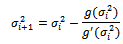 where;
where;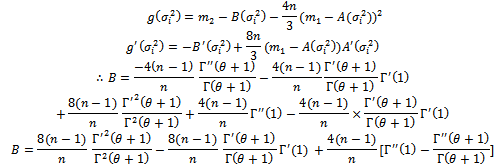
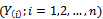 denotes the ordered sample, where:
denotes the ordered sample, where: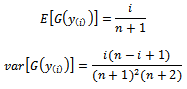 The
The 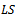 estimators for the unknown parameters
estimators for the unknown parameters 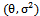 of the proposed
of the proposed 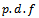 of Generalized Rayleigh with two parameters
of Generalized Rayleigh with two parameters 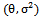 in case of outlier (i.e equation 3), and its
in case of outlier (i.e equation 3), and its 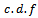 (equation 5), can be obtained by minimizing the quantity T, defined in equation (19):
(equation 5), can be obtained by minimizing the quantity T, defined in equation (19):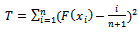
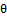 and
and 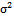 :
: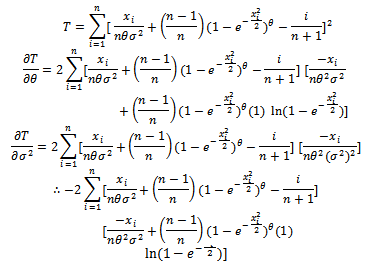
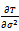 :
: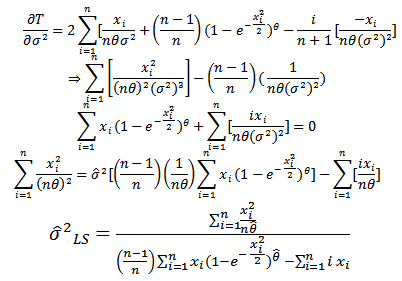
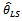 is estimated from equation (20) which is non linear equation can be solved using Newton Raphson method, or we can use Moment estimator of
is estimated from equation (20) which is non linear equation can be solved using Newton Raphson method, or we can use Moment estimator of 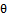 (equation 17) to obtain least square estimator of parameter (
(equation 17) to obtain least square estimator of parameter (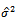 ), and then obtain the mixed estimator.
), and then obtain the mixed estimator.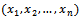 are such that
are such that 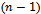 of them are distributed with
of them are distributed with  and one variable is distributed with
and one variable is distributed with 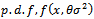 , so the joint distribution of
, so the joint distribution of 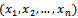 are:
are: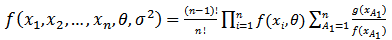
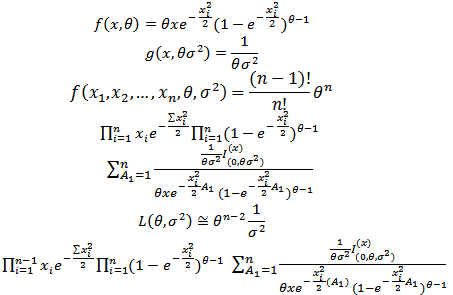
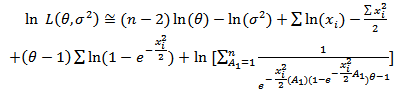
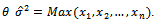
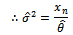
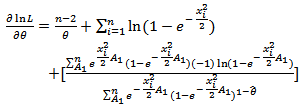
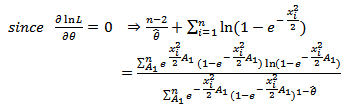
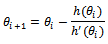 to obtai
to obtai 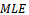 for
for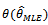 .Summary1. The
.Summary1. The 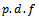 of
of 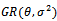 in presence of outlier is defined in equation (1).2. The
in presence of outlier is defined in equation (1).2. The 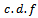 is obtained in closed from equation (5).3. The Moment Generating function is derived and written in a closed from equation (10).4. First and second Moments of this distribution are obtained equation (12) and equation (13).5. Moment's estimator's can be obtained from equation (14) and (15) using Newton Raphson formula (16) and (18).6. Since the
is obtained in closed from equation (5).3. The Moment Generating function is derived and written in a closed from equation (10).4. First and second Moments of this distribution are obtained equation (12) and equation (13).5. Moment's estimator's can be obtained from equation (14) and (15) using Newton Raphson formula (16) and (18).6. Since the 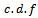 was found in closed from equation (5), it can be used to find the LS estimator, through minimizing equation (19), the estimators of LS are obtained from equations (20, 21).7. The Likelihood function is defined in equations (21), (22) and (23), and then the Maximum Likelihood estimator's are explained in equations (24) and (25).8. Any estimators of Moments, LS can be used in MLE to obtain the Mixture estimators.
was found in closed from equation (5), it can be used to find the LS estimator, through minimizing equation (19), the estimators of LS are obtained from equations (20, 21).7. The Likelihood function is defined in equations (21), (22) and (23), and then the Maximum Likelihood estimator's are explained in equations (24) and (25).8. Any estimators of Moments, LS can be used in MLE to obtain the Mixture estimators.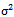 , and shape parameter
, and shape parameter 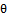 ), and consist of mixing the distribution of
), and consist of mixing the distribution of 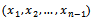 random variables with the distribution of random variable (
random variables with the distribution of random variable (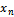 ), i.e (the distribution of
), i.e (the distribution of 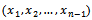 is Rayleigh distribution with (
is Rayleigh distribution with (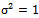 ) and
) and 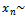 uniformly with
uniformly with 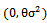 , and the replicate each experiment (R=1000), and to use mean square error (MSE) or integrated mean square error (IMSE) for comparison. We have studied various method for estimating the parameters, (Least Squares, Moments, Mixture), and derived the Moment Generating function, which is used to obtain the first and second Moment of this
, and the replicate each experiment (R=1000), and to use mean square error (MSE) or integrated mean square error (IMSE) for comparison. We have studied various method for estimating the parameters, (Least Squares, Moments, Mixture), and derived the Moment Generating function, which is used to obtain the first and second Moment of this 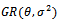 , and then used as a possible alternative method for estimating Parameters.This work will be done in another suggestion in future, to apply this method on another distribution.
, and then used as a possible alternative method for estimating Parameters.This work will be done in another suggestion in future, to apply this method on another distribution. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML