-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2012; 2(6): 169-177
doi: 10.5923/j.ajms.20120206.02
On Basis Properties of Function Systems in Lebesgue Spaces
Bilalov B. T. , Garayev T. Z.
Institute of Mathematics and Mechanics of NAS of Azerbaijan
Correspondence to: Bilalov B. T. , Institute of Mathematics and Mechanics of NAS of Azerbaijan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Some approximative issues related to function systems in Lebesgue spaces are treated in this work, such as the continuation of basis, the non-minimality of basis in subinterval, the relationship between completeness and minimality of sine and cosine type systems. It is proved that the basis properties of sines and cosines type systems in Lebesgue space of functions depend on the number of exponential summands in expressions of these systems.
Keywords: Completeness, Minimality, Lebesgue Space Classification 2000: 30B60, 42A65, 46B15
Cite this paper: Bilalov B. T. , Garayev T. Z. , "On Basis Properties of Function Systems in Lebesgue Spaces", American Journal of Mathematics and Statistics, Vol. 2 No. 6, 2012, pp. 169-177. doi: 10.5923/j.ajms.20120206.02.
Article Outline
1. Introduction
- The study of approximative properties of function systems in Lebesgue spaces represents special scientific interest for applications in various areas of mathematics. In particular, these matters are important in the spectral theory of differential operators and in the theory of wavelet analysis. Obvious examples are the classical systems of exponentials, sines, cosines, and their perturbation. Approximative properties of these systems in various functional spaces are well studied, and there are extensive bibliographies devoted to them (see, e.g.[1-5]). Relationship between the basis properties of these systems are known, and it is not difficult to establish it. In general, systems of sines and cosines can be written as follows
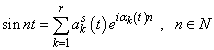 ;
;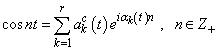 ,where
,where  , N is the set of all positive integers,
, N is the set of all positive integers,  and
and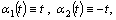
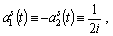
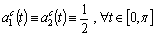 .It is easy to see that the set of values of the functions
.It is easy to see that the set of values of the functions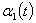 and
and 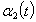 fill up the whole segment
fill up the whole segment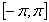 , where the basis properties of the system of exponentials
, where the basis properties of the system of exponentials 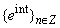 (
(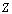 are integers ) are examined. Considering the generalization of this case, we obtain a system of the following form
are integers ) are examined. Considering the generalization of this case, we obtain a system of the following form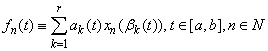 | (1) |
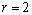 ( i.e. the number of exponential summands) plays an important role in studying of the basis properties of systems of sines and cosines. We will establish some relations between the basis properties of systems
( i.e. the number of exponential summands) plays an important role in studying of the basis properties of systems of sines and cosines. We will establish some relations between the basis properties of systems  and
and  considered in various Banach spaces. We assume that the system
considered in various Banach spaces. We assume that the system 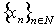 is defined on the segment
is defined on the segment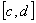 . It is interesting that, under natural conditions on functions
. It is interesting that, under natural conditions on functions 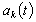 and
and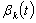 ,
, 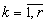 , if the system
, if the system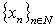 forms a basis for
forms a basis for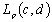 , then the system
, then the system 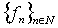 is non-minimal in
is non-minimal in 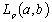 for
for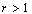 . This phenomenon does not happen in the case of the system of exponentials
. This phenomenon does not happen in the case of the system of exponentials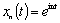 ,
, 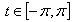 , since in this case we deal with
, since in this case we deal with 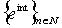 (or
(or 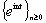 if a system of cosines is considered), the half of the basis
if a system of cosines is considered), the half of the basis 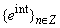 . Apparently similar problem is considered for the first time. These and other approximative properties of systems are closely related to the matters of continuation of the basis on a wide interval which have previously been considered in[5-7].
. Apparently similar problem is considered for the first time. These and other approximative properties of systems are closely related to the matters of continuation of the basis on a wide interval which have previously been considered in[5-7].2. Main Assumptions and Auxiliary Facts
- Let [a,b] be a segment on the real axis
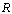 . As usual, by
. As usual, by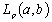 ,
, 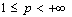 we mean a Lebesgue space of functions whose absolute value raised to the pth power is summable in
we mean a Lebesgue space of functions whose absolute value raised to the pth power is summable in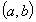 . The norm in this space is defined as
. The norm in this space is defined as 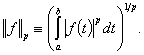 It is known that
It is known that 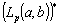 is isometrically isomorphic to
is isometrically isomorphic to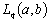 , where
, where 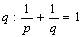 is a number conjugated to
is a number conjugated to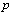 . In other words
. In other words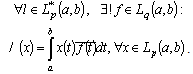 .Let us state some ideas from the theory of bases. Let
.Let us state some ideas from the theory of bases. Let 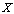 be some Banach space and
be some Banach space and 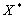 be its conjugate. We denote by
be its conjugate. We denote by 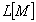 the linear span of the set
the linear span of the set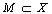 , and
, and 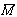 will be the closure of
will be the closure of 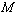 in
in 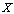 . We will assume that all the considered spaces are complex. Definition 1. System
. We will assume that all the considered spaces are complex. Definition 1. System 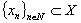 is called complete in
is called complete in 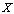 if
if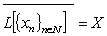 .Definition 2. System
.Definition 2. System 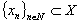 is called minimal in X if
is called minimal in X if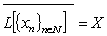 ,
,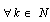 .The following criteria of these properties are well knownStatement 1. System
.The following criteria of these properties are well knownStatement 1. System 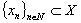 is complete in
is complete in 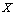 if and only if from
if and only if from 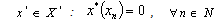 , it follows that
, it follows that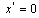 .Statement 2. System
.Statement 2. System 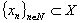 is minimal in
is minimal in 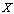 if and only if
if and only if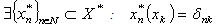 ,
, 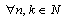 , where
, where 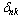 is the Kronecker symbol. Recall also the definition of the basisDefinition 3. System
is the Kronecker symbol. Recall also the definition of the basisDefinition 3. System 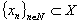 forms a basis for
forms a basis for 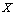 if for
if for 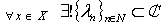 :
: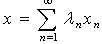 , where
, where 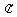 is a field of complex numbers.More details of these and other facts from the theory of bases can be found in the monographs [8-11]. Thus, the completeness of the system
is a field of complex numbers.More details of these and other facts from the theory of bases can be found in the monographs [8-11]. Thus, the completeness of the system 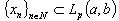 is equivalent to the fact that
is equivalent to the fact that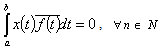 ,
, 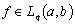 , implies
, implies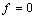 . Minimality of the system
. Minimality of the system 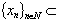
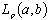 means that
means that 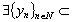
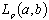 :
: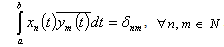 .We make the following basic assumptions concerning functions
.We make the following basic assumptions concerning functions 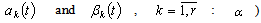
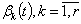 , are piecewise smooth, monotonous functions on
, are piecewise smooth, monotonous functions on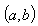 ; moreover,
; moreover, 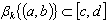
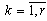 ,, and
,, and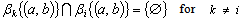 , where
, where 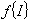 denotes the image of the set
denotes the image of the set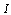 , i.e.
, i.e. 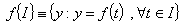 .
.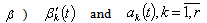 are measurable functions on
are measurable functions on 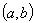 and the inequality
and the inequality 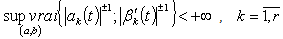 holds, where
holds, where 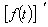 enotes the derivative of
enotes the derivative of 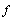 in t.Throughout this paper we will use the notation
in t.Throughout this paper we will use the notation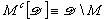 .
. 2.1. Continuation of the Basis
- Let systems
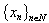 and
and 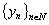 form bases for spaces
form bases for spaces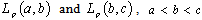 , respectively. By
, respectively. By 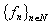 and
and 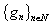 we denote the corresponding biorthogonal systems. Let’s consider arbitrary functions
we denote the corresponding biorthogonal systems. Let’s consider arbitrary functions 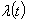 and
and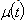 :
: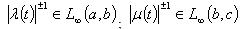 .We introduce the following functions
.We introduce the following functions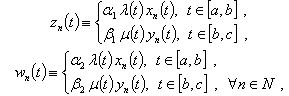 where
where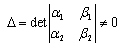 .Consider the double system
.Consider the double system 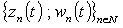 | (2) |
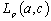 , and the system
, and the system 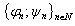 biorthogonal to it has the following form
biorthogonal to it has the following form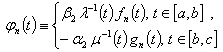
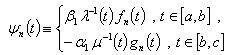 In fact
In fact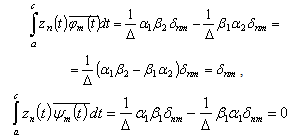 Similarly we can show that
Similarly we can show that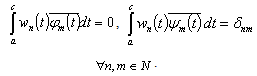 .Now let us prove the completeness of the system (2) in
.Now let us prove the completeness of the system (2) in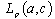 . Let the following relations be true for some
. Let the following relations be true for some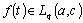 :
: 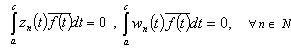 .We have
.We have 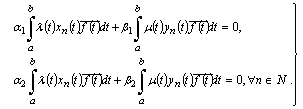 From
From  it follows that
it follows that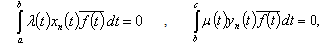
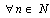 . Consequently,
. Consequently, 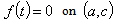 , and this proves the completeness of the system (2) in
, and this proves the completeness of the system (2) in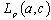 .Let us consider
.Let us consider 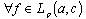 and the partial sum
and the partial sum 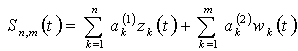 ,where
,where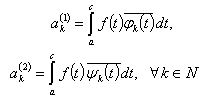 .Denote
.Denote 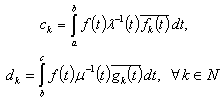 .Then
.Then 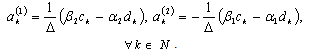 .Let
.Let 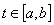 . In this case we have
. In this case we have 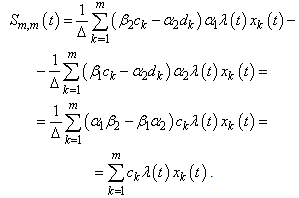 Similarly, for
Similarly, for 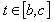 we have
we have 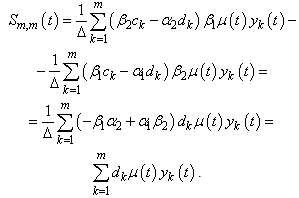 From these relations it follows that
From these relations it follows that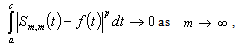 ,and thus, the double system (2) forms a basis for
,and thus, the double system (2) forms a basis for 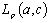 if summation is made symmetrically, i.e. this system forms a symmetrical basis for
if summation is made symmetrically, i.e. this system forms a symmetrical basis for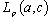 .
.2.2. Some Approximative Properties of Function Systems in Lebesgue Spaces
- By
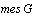 e mean the Lebesgue measure of the set
e mean the Lebesgue measure of the set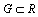 . All the subsets of real axis we consider are assumed to be Lebesgue measurable. It is easily seen that if the system
. All the subsets of real axis we consider are assumed to be Lebesgue measurable. It is easily seen that if the system 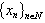 is minimal in
is minimal in 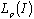 , then it is also minimal in
, then it is also minimal in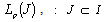 ; and if it is complete in
; and if it is complete in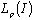 , then it is also complete in
, then it is also complete in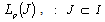 . An interesting fact should be noted that the system
. An interesting fact should be noted that the system 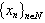 can be complete and minimal at the same time in
can be complete and minimal at the same time in 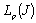 and in
and in 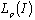 for
for 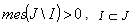 . Relevant nontrivial example can be found e.g. in [6]. In the case of basis we have the following Lemma 1. If the system
. Relevant nontrivial example can be found e.g. in [6]. In the case of basis we have the following Lemma 1. If the system 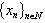 forms a basis for
forms a basis for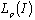 ,
, 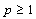 , then it is nonminimal in
, then it is nonminimal in 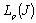 for
for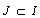 :
: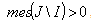 .In fact, let this system be minimal in
.In fact, let this system be minimal in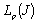 , and let
, and let 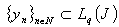 be a corresponding biorthogonal system. Assume
be a corresponding biorthogonal system. Assume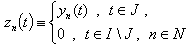 Evidently,
Evidently, 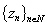 is a system biorthogonal to
is a system biorthogonal to 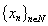 in
in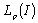 . Taking the function
. Taking the function 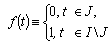 Moreover, a basis in
Moreover, a basis in 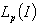 can be complete also in
can be complete also in 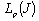 for
for 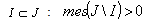 (it is minimal in
(it is minimal in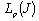 , of course). Let us give an appropriate example. Let us take an arbitrary orthonormal basis
, of course). Let us give an appropriate example. Let us take an arbitrary orthonormal basis 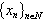 in
in 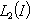 . Let
. Let 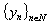 be some complete system in
be some complete system in 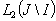 (in case when
(in case when 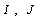 are intervals, we can easily make such a choice). Assume
are intervals, we can easily make such a choice). Assume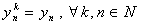 , and construct a new system
, and construct a new system 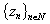 in the following way
in the following way 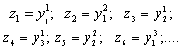 Let us consider the system
Let us consider the system 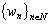 defined by the expression
defined by the expression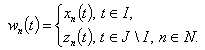 | (3) |
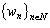 forms a basis for
forms a basis for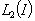 . Show that it is complete in
. Show that it is complete in 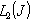 . Let
. Let 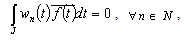 for some
for some 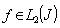 . It follows from construction of
. It follows from construction of 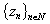 and (3) that for
and (3) that for 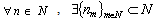 :
: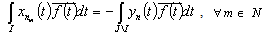 .Evidently,
.Evidently, 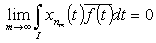 , and, as a result,
, and, as a result, 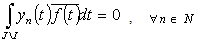 . It follows from completeness of the system
. It follows from completeness of the system 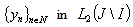 that
that 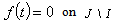 . The further reasoning is obvious.
. The further reasoning is obvious.3. Main Results
3.1. Single Case
- We proceed to the main results. Let us consider the system (1). The following theorem is true. Theorem 1. Let the conditions
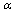 ),
),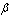 ) be fulfilled. Then : 1) it follows from the completeness of the system
) be fulfilled. Then : 1) it follows from the completeness of the system 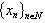 in
in 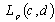 that the system
that the system 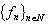 is complete in
is complete in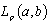 ; 2) from minimality of the system
; 2) from minimality of the system 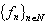 in
in 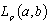 it follows that the system
it follows that the system 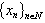 is minimal in
is minimal in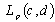 ,
,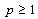 .Proof. Let us take any function
.Proof. Let us take any function 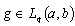 and consider
and consider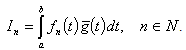 | (4) |
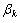 are increasing. We denote by
are increasing. We denote by 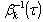 an inverse of the function
an inverse of the function 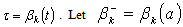 ,
,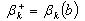 . We set
. We set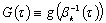 ,
,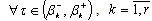 . Let us assume
. Let us assume 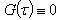 ,
, 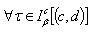 , where
, where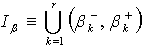 , and introduce the function
, and introduce the function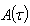 :
: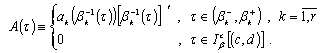 Under these notations, the integrals
Under these notations, the integrals 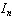 can be written as follows
can be written as follows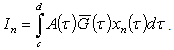 | (5) |
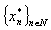 and
and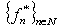 , are biorthogonal to the systems
, are biorthogonal to the systems 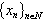 and
and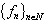 , respectively, are related by the following formula
, respectively, are related by the following formula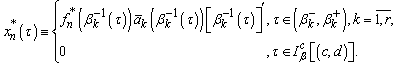 | (6) |
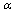 ),
),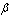 ) be fulfilled. Then, if the system
) be fulfilled. Then, if the system 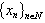 forms a basis for
forms a basis for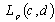 ,
,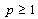 , and
, and 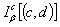 contains a nontrivial interval ( i.e.
contains a nontrivial interval ( i.e. 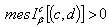 ), then the system
), then the system 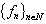 is nonminimal in
is nonminimal in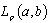 .The validity of the theorem follows directly from Lemma 1 and (6). The following result was absolutely unexpected for the authors.Theorem 3. Let the conditions
.The validity of the theorem follows directly from Lemma 1 and (6). The following result was absolutely unexpected for the authors.Theorem 3. Let the conditions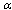 ),
),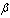 ) be fulfilled and
) be fulfilled and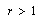 . Then if
. Then if 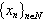 forms a basis for
forms a basis for 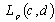 , then the system
, then the system 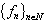 is nonminimal in
is nonminimal in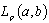 ,
,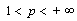 .Proof. Let
.Proof. Let 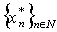 be a system biorthogonal to
be a system biorthogonal to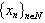 . It is evident that the system
. It is evident that the system 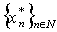 forms a basis for
forms a basis for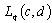 . Consequently, this system is nonminimal in
. Consequently, this system is nonminimal in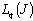 , where
, where 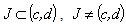 is any interval. Assume that the system
is any interval. Assume that the system 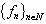 is minimal in
is minimal in 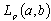 and
and 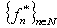 is a system biorthogonal to it. The uniqueness of a system biotrhogonal to the complete one and the relation (6) imply that
is a system biorthogonal to it. The uniqueness of a system biotrhogonal to the complete one and the relation (6) imply that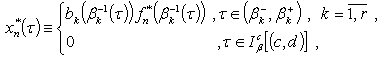 where
where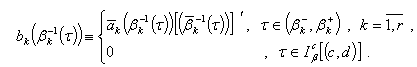 Without loss of generality, we will assume that
Without loss of generality, we will assume that 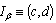 . Since doing otherwise we would have, by virtue of Theorem 2, that the system
. Since doing otherwise we would have, by virtue of Theorem 2, that the system 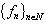 is nonminimal in
is nonminimal in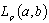 . Let us introduce the function
. Let us introduce the function 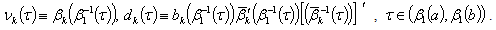 .We have
.We have 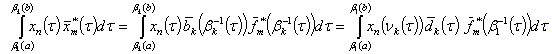 .On the other hand
.On the other hand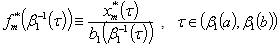 .As a result we obtain
.As a result we obtain 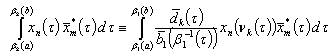 .Summing this equality over
.Summing this equality over  from
from  to
to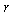 , we have
, we have 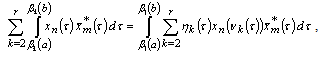 | (7) |
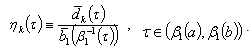 It is obvious that
It is obvious that 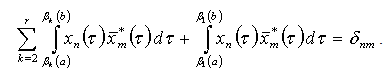 Taking into account this expression in (7), we obtain
Taking into account this expression in (7), we obtain 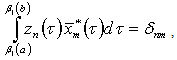 where
where 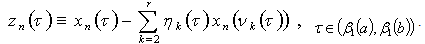 It is easy to see that
It is easy to see that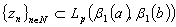 , and, consequently,
, and, consequently, 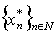 is minimal in
is minimal in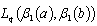 . Evidently,
. Evidently, 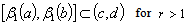 . So we have a contradiction by virtue of Lemma 1.The theorem is proved.Corollary 1. System
. So we have a contradiction by virtue of Lemma 1.The theorem is proved.Corollary 1. System 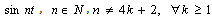 , is complete i
, is complete i 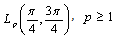 .In fact, the apparent equality
.In fact, the apparent equality 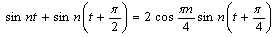 ,and Theorem 1 imply that the system
,and Theorem 1 imply that the system 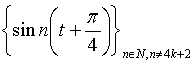 is complete in
is complete in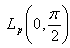 .
.3.2. Double Case
- The similar conclusions can be made for the following function systems
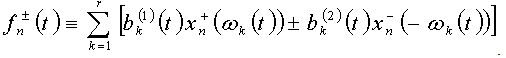 In this case we assume that the functions
In this case we assume that the functions 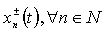 , are defined on the segment
, are defined on the segment 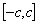 . Let the following conditions be satisfied:
. Let the following conditions be satisfied: 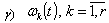 , are piecewise smooth, monotonous functions on
, are piecewise smooth, monotonous functions on 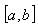 with
with 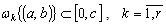 ;
;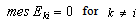 , where
, where 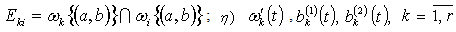 , are measurable functions on
, are measurable functions on 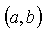 with
with 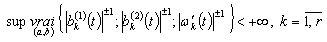 Assume
Assume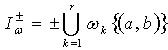 . Introduce
. Introduce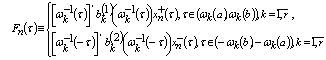 , and consider the following double systemsIt is easy to prove the followingTheorem 4. Let the conditions
, and consider the following double systemsIt is easy to prove the followingTheorem 4. Let the conditions  be fulfilled. Then: 1) if the system (81), ((82)) is complete in
be fulfilled. Then: 1) if the system (81), ((82)) is complete in 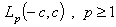 , then the systems
, then the systems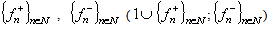 are complete in
are complete in 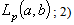 it follows from the minimality of the systems
it follows from the minimality of the systems 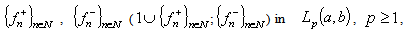 that the systems (81) ((82)) are minimal in
that the systems (81) ((82)) are minimal in 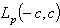 .In fact, let us take
.In fact, let us take 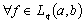 and suppos
and suppos 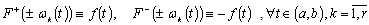 .We have
.We have 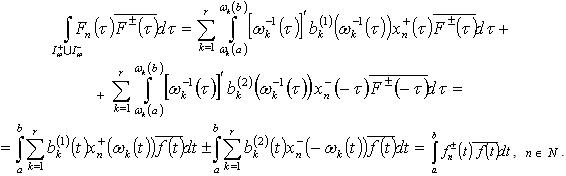 Thus
Thus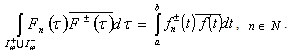 | (9) |
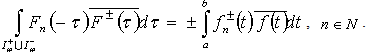 | (10) |
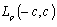 implies the completeness of each of the systems
implies the completeness of each of the systems 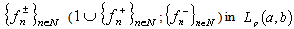 .Let us assume that the systems
.Let us assume that the systems 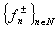 are minimal in
are minimal in 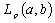 and
and 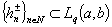 are the corresponding biorthogonal systems. Assume
are the corresponding biorthogonal systems. Assume 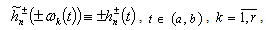 and consider the system
and consider the system 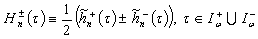 | (11) |
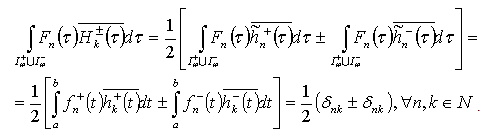 Similarly we obtain
Similarly we obtain 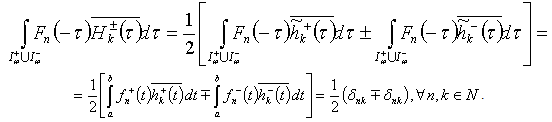 .From these relations we obtain the minimality of system (81) ((82)) in
.From these relations we obtain the minimality of system (81) ((82)) in 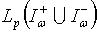 .The following theorem is valid.Theorem 5. Let the conditions
.The following theorem is valid.Theorem 5. Let the conditions 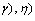 be fulfilled. If the system (81) ((82)) forms a basis for
be fulfilled. If the system (81) ((82)) forms a basis for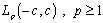 , and
, and 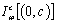 contains a non-trivial interval, then at least one of the systems
contains a non-trivial interval, then at least one of the systems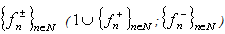 is non-minimal in
is non-minimal in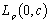 .This theorem is an analogue of Theorem 2 for double systems. The below theorem which is an analogue of Theorem 3 is valid as well.Theorem 6. Let the condition
.This theorem is an analogue of Theorem 2 for double systems. The below theorem which is an analogue of Theorem 3 is valid as well.Theorem 6. Let the condition 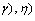 be fulfilled and
be fulfilled and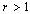 . If the system (81) ((82)) forms a basis for
. If the system (81) ((82)) forms a basis for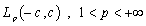 , then at least one of the systems
, then at least one of the systems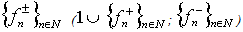 is non-minimal in
is non-minimal in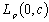 .In fact, let the systems
.In fact, let the systems 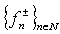 be minimal in
be minimal in 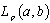 . If
. If 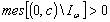 , then we have a contradiction by virtue of Lemma 1. Therefore we will assume that
, then we have a contradiction by virtue of Lemma 1. Therefore we will assume that 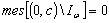 . It is evident that the system biorthogonal to (81) is defined by the relation (11). Denote by
. It is evident that the system biorthogonal to (81) is defined by the relation (11). Denote by 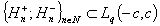 the system biorthogonal to (81). It is easily seen that
the system biorthogonal to (81). It is easily seen that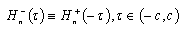 . Let us assume
. Let us assume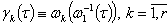 . From relations (11) we derive
. From relations (11) we derive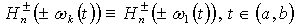 .Taking into account the latter relation, we have
.Taking into account the latter relation, we have 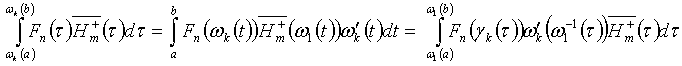 .Hence
.Hence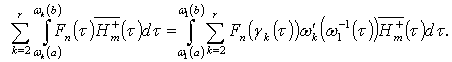 In the same manner we get
In the same manner we get 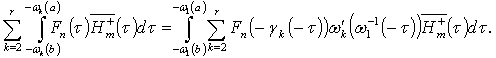 Consequently
Consequently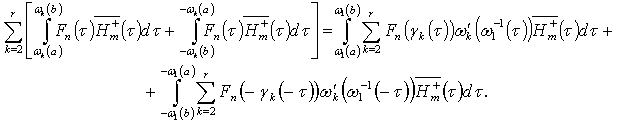 Continuing in the same way as we did when proving Theorem 3, we finish the proof of Theorem 6. This theorem is an analogue of Theorem 3 for double systems. Using these two theorems, we come to the following Corollary 2. Let
Continuing in the same way as we did when proving Theorem 3, we finish the proof of Theorem 6. This theorem is an analogue of Theorem 3 for double systems. Using these two theorems, we come to the following Corollary 2. Let 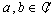 be arbitrary non-trivial complex numbers. Then each of the systems
be arbitrary non-trivial complex numbers. Then each of the systems 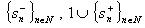 is complete in
is complete in ,
,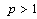 . However, at least one of them is nonminimal in it with
. However, at least one of them is nonminimal in it with 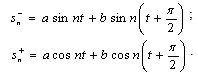 .In fact, denoting
.In fact, denoting 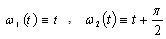 and
and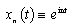 , we can apply Theorem 6 to this system.It should be noted that some relationship between the unitary and double power systems are considered in [12-14].
, we can apply Theorem 6 to this system.It should be noted that some relationship between the unitary and double power systems are considered in [12-14].4. Conclusions
- Summing up, we arrive at the following conclusions:1) a method for constructing a basis in the direct product of Lebesgue spaces is suggested;2) it is shown that if the system of functions forms a basis for Lebesgue space
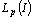 , then it is not minimal in
, then it is not minimal in 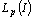 for
for 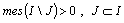 ;3) let us reduce an example of the basis in
;3) let us reduce an example of the basis in 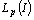 , which is complete in
, which is complete in 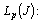
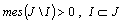 ;4) the unitary system of the form (1) is considered and some relations between the basis properties of the systems
;4) the unitary system of the form (1) is considered and some relations between the basis properties of the systems 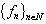 and
and 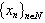 is established;5) it is proved that for
is established;5) it is proved that for 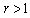 , from the basicity of the system
, from the basicity of the system 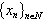 follows the nonminimality of the system
follows the nonminimality of the system 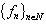 ;6) analogous results is obtained with respect to the double system of functions.
;6) analogous results is obtained with respect to the double system of functions.ACKNOWLEDGEMENTS
- The authors are thankful to the reviewers for their valuable comments.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML , Dokl. RAN, 1992, v.322, No 6, pp. 1019-1021.
, Dokl. RAN, 1992, v.322, No 6, pp. 1019-1021.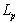 . Sibirsk. Mat. Zh., 2006, v.47. No 1, pp. 25-36.
. Sibirsk. Mat. Zh., 2006, v.47. No 1, pp. 25-36.