Atikur Rahman Baizid 1, Md. Shah Alam 2
1Department of Business Administration, Leading University, Sylhet, 3100, Bangladesh
2Department of Physics, Shahjalal University of Science and Technology, Sylhet, 3114, Bangladesh
Correspondence to: Atikur Rahman Baizid , Department of Business Administration, Leading University, Sylhet, 3100, Bangladesh.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The Lorentz transformation is well known. In this paper, we have presented various types of applications of different Lorenz Transformations according to the nature of movement of one inertial frame relative to the other inertial frame such as relativistic aberration, relativistic Doppler’s effect and reflection of light ray by a moving mirror. When one frame moves along X- axis with respect to the rest frame then we can find these applications for special Lorentz transformation. When the motion of the moving frame is not along X-axis relative to the rest frame but the motion is along any arbitrary direction then we can find these formulae for most general Lorentz transformation. We can generate these formulae for different types of most general Lorentz transformations using mixed number, quaternion and geometric product.
Keywords:
Special Lorentz Transformation, Most General, Mixed Number, Quaternion, Geometric Product, Relativistic Aberration, Relativistic Doppler’s Effect, Reflection of Light Ray
1. Introduction
1.1. Special Lorentz Transformation
Let us consider two inertial frames of reference S and S′ , where the frame S is at rest and the frame S′ is moving along the X-axis with velocity v with respect to the S frame. The space and time co-ordinates of S and S′ are (x, y, z, t) and (x′, y′, z′, t′) respectively. The relation between the co-ordinates of S and S′ is called the special Lorentz transformation[1] which can be written as 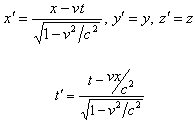 | (1) |
and the inverse special Lorentz transformation[1] can be written as 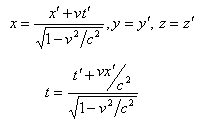 | (2) |
1.2. Most General Lorentz Transformation
When the motion of the moving frame is along any arbitrary direction instead of the X-axis , i.e. , the velocity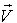 has three components Vx , Vy and Vz , then the relation between the space and time co-ordinates of S and
has three components Vx , Vy and Vz , then the relation between the space and time co-ordinates of S and 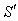 is called the most general Lorentz transformation[2] which can be written as
is called the most general Lorentz transformation[2] which can be written as 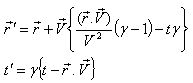 | (3) |
and the inverse most general Lorentz transformation[2] which can be written as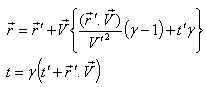 | (4) |
Where , 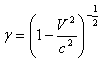 and
and 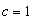
1.3. Mixed Number Lorentz Transformation
In the case of the most general Lorentz transformation, the velocity 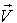 of
of 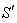 with respect to
with respect to 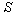 is not along the X-axis; i.e., the velocity
is not along the X-axis; i.e., the velocity 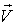 has three components, Vx, Vy, and Vz. Let in this case
has three components, Vx, Vy, and Vz. Let in this case 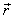 and
and 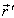 be the space parts in
be the space parts in 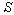 and
and 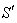 frames, respectively. Then using the mixed product
frames, respectively. Then using the mixed product 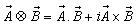 , the mixed number Lorentz transformations[3– 6] can be written as
, the mixed number Lorentz transformations[3– 6] can be written as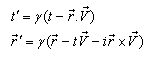 | (5) |
and the inverse mixed number Lorentz transformation[3– 6], can be written as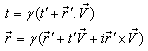 | (6) |
Let, 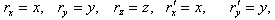
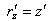 . If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to
. If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to  then equation (5) and (6) can be written as
then equation (5) and (6) can be written as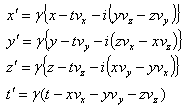 | (7) |
and 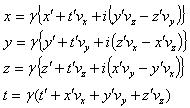 | (8) |
1.4. Quaternion Lorentz Transformation
In this case the velocity 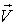 of
of 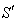 with respect to
with respect to 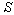 has also three components, Vx, Vy, and Vz as the most general Lorentz transformation. Let in this case
has also three components, Vx, Vy, and Vz as the most general Lorentz transformation. Let in this case 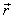 and
and 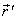 be the space parts in
be the space parts in 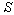 and
and 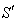 frames respectively. Then using the quaternion product
frames respectively. Then using the quaternion product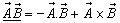 the quaternion Lorentz transformation[7-10] can be written as
the quaternion Lorentz transformation[7-10] can be written as 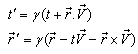 | (9) |
and the inverse quaternion Lorentz transformation[7-10] can be written as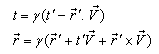 | (10) |
Let, 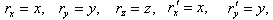
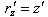 .If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to
.If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to 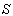 then equation (9) and (10) can be written as
then equation (9) and (10) can be written as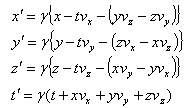 | (11) |
and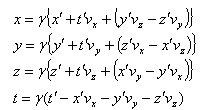 | (12) |
1.5. Geometric Product Lorentz Transformation
In this case the velocity 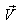 of S' with respect to
of S' with respect to 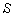 has also three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case
has also three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case 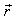 and
and 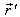 be the space parts in
be the space parts in 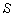 and
and 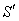 frames respectively. Then using the geometric product of two vectors
frames respectively. Then using the geometric product of two vectors 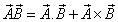 the geometric product Lorentz transformation[11, 12] can be written as
the geometric product Lorentz transformation[11, 12] can be written as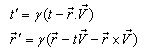 | (13) |
and the inverse geometric product Lorentz transformation,[11, 12] can be written as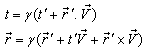 | (14) |
Let, 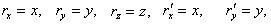
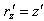 .If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to
.If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to 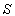 then equation (13) and (14) can be written as
then equation (13) and (14) can be written as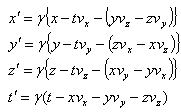 | (15) |
and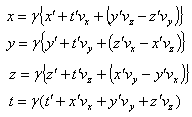 | (16) |
Now we are going to derive the formulae for relativistic aberration, relativistic Doppler’s effect and reflection of light ray by a moving mirror of different types of lorentz transformations respectively.
2. Aberration
The speed of light is independent of the medium of transmission but the direction of light rays depends on the motion of the source emitting light and observer[10]
2.1. Relativistic Aberration of Special Lorentz Transformation
The earth moves round the sun in its orbit. Consider sun is to be the system 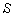 and the earth is in the system
and the earth is in the system 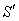 is moving with velocity V relative to the system
is moving with velocity V relative to the system 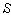 along positive direction of common X-axis. Let the star P observed from the observers
along positive direction of common X-axis. Let the star P observed from the observers 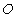 and
and 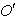 in system
in system 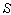 and
and 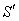 where the frame
where the frame 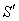 is moving along X-axis with velocity V with respect to
is moving along X-axis with velocity V with respect to 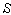 frame. Let the angles made by the light ray in X-Y plane from the star P at any instant in two systems at
frame. Let the angles made by the light ray in X-Y plane from the star P at any instant in two systems at 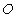 and
and 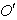 be
be 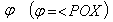 and
and 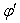
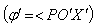 respectively[Figure 1].
respectively[Figure 1].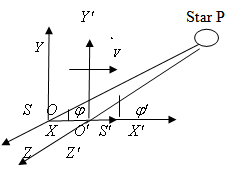 | Figure 1. Direction of light rays observed from a fixed frame 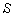 and a moving frame and a moving frame 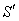 (the frame (the frame 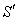 is moving along common X-axis with velocity V with respect to is moving along common X-axis with velocity V with respect to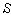 frame) frame) |
It can be shown that[13]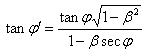 where
where 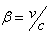 | (17) |
and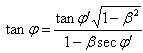 | (18) |
It is clear from equation (17) and (18), 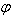 and
and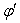 are not same in the two systems; they depend upon the motion of source and observer. Hence equation (17) describes the relativistic aberration of special Lorentz transformation.
are not same in the two systems; they depend upon the motion of source and observer. Hence equation (17) describes the relativistic aberration of special Lorentz transformation.
2.2. Relativistic Aberration of Most General Lorentz Transformation
Consider the light from a star P observed by the observers 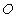 and
and 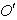 in system
in system 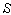 and
and 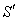 where the frame
where the frame 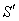 is moving along any arbitrary direction with velocity
is moving along any arbitrary direction with velocity 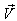 with respect to
with respect to 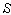 frame as shown in figure -2. Let the angles made by the light ray in X-Y plane from the star P at any instant in two systems at
frame as shown in figure -2. Let the angles made by the light ray in X-Y plane from the star P at any instant in two systems at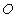 and
and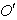 be
be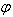
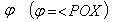 and
and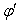
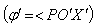 respectively. Here the angle
respectively. Here the angle 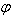 is same in Fig. 1 and 2. But the angle
is same in Fig. 1 and 2. But the angle 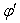 is different Fixed Moving
is different Fixed Moving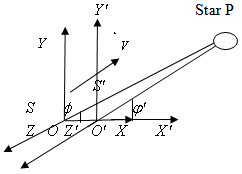 | Figure 2. Direction of light rays observed from a fixed frame  and a moving frame and a moving frame  ( the frame ( the frame  is moving along any arbitrary direction with velocity V with respect to is moving along any arbitrary direction with velocity V with respect to  frame) frame) |
It also can be shown that for two dimension case, the Relativistic aberration of most general Lorentz transformation is clear which has been described[10] by the following relationship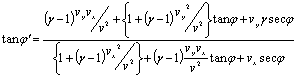 | (19) |
From equation (19), we have 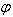 and
and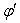 are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (19) gives the relativistic formula for aberration of most general Lorentz transformation.
are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (19) gives the relativistic formula for aberration of most general Lorentz transformation.
2.3. Relativistic Aberration of Mixed Number Lorentz Transformation
Consider the same situation as described in Figure 2. Let, 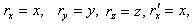
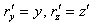 ,then using equation (5) and (6) we can easily find out the aberration formula for two dimension case of the mixed number Lorentz transformation[10]
,then using equation (5) and (6) we can easily find out the aberration formula for two dimension case of the mixed number Lorentz transformation[10]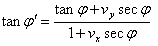 | (20) |
From equation (20), we have 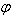 and
and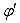 are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (20) gives the relativistic formula for aberration of mixed number Lorentz transformation.
are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (20) gives the relativistic formula for aberration of mixed number Lorentz transformation.
2.4. Relativistic Aberration of Quaternion Lorentz Transformation
Consider the same situation as described in Figure 2. Let, 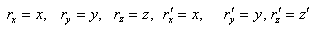 then using equation (9) and (10) we can easily find out the aberration formula for two dimension case of the quaternion Lorentz transformation[14]
then using equation (9) and (10) we can easily find out the aberration formula for two dimension case of the quaternion Lorentz transformation[14]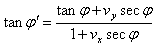 | (21) |
2.5. Relativistic Aberration of Geometric Product Lorentz Transformation
Consider the same situation as described in figure 2. Let, 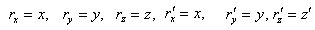 Equation (13) can be written as
Equation (13) can be written as 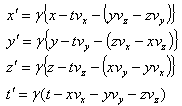 | (22) |
Differentiating both sides of equation (22) we get 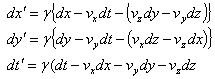 from the above equation we have
from the above equation we have 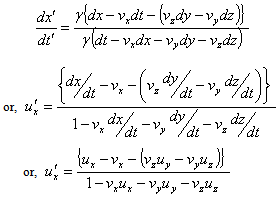 | (23) |
and 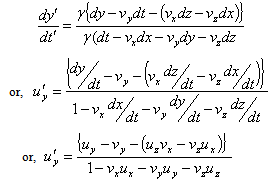 | (24) |
Dividing equation (23) and (24) we get 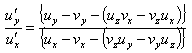 If we consider two dimension case, then we can write
If we consider two dimension case, then we can write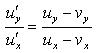 | (25) |
In this case the star light travelling in x-y plane with velocity c, has component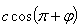 and
and 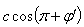 along positive direction of X-axis in system
along positive direction of X-axis in system 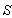 and
and 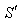 respectively. Also those
respectively. Also those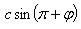 and
and 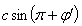 are along positive direction of Y-axis in system
are along positive direction of Y-axis in system 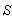 and
and 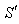 respectively. Thus we have
respectively. Thus we have 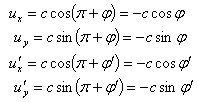 | (26) |
From Equation (25) and (26) we have 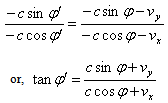 Considering
Considering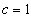 we have
we have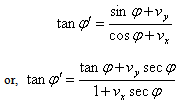 | (27) |
From equation (27), we have 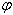 and
and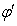 are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (27) gives the relativistic formula for aberration of geometric product Lorentz transformation.
are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (27) gives the relativistic formula for aberration of geometric product Lorentz transformation.
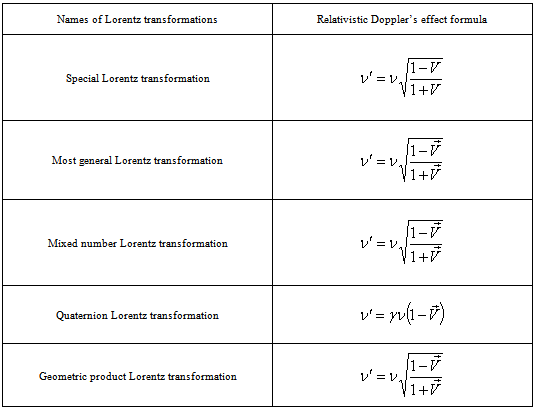
3. Relativistic Doppler’s Effect
The Doppler’s effect[15] is an apparent change in frequency of a wave that results from the motion of source or observer or both. The relativistic Doppler’s effect[16] is the change in frequency and wavelength of light, caused by the relative motion of the source and observer such as in the regular Doppler’s effect, when taking into account effects of special theory of relativity. The relativistic Doppler’s effect is different from the true (non – relativistic) Doppler’s effect as the equations include the time dilation effect of the special relativity. They described the total difference in the frequencies and possess the Lorentz symmetry.We can analyse the Doppler’s effect[17] of light by considering a light source as a clock that ticks 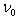 times per second and emits a wave of light with each tick. In the case of observer receding from the light source, the observer travels the distance
times per second and emits a wave of light with each tick. In the case of observer receding from the light source, the observer travels the distance 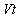 away from the source between the ticks, which mean that the light wave from a given tick takes
away from the source between the ticks, which mean that the light wave from a given tick takes 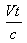 longer to reach him than the previous one. Hence the total time between the arrivals of successive waves is
longer to reach him than the previous one. Hence the total time between the arrivals of successive waves is 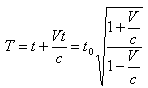 and the observed frequency is
and the observed frequency is 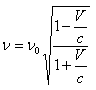 In the case of observer approaching the light source, the observed frequency is
In the case of observer approaching the light source, the observed frequency is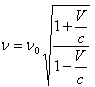 | (28) |
3.1. Relativistic Doppler’s Effect of Special Lorentz Transformation
Consider two frames of references 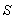 and
and 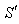 where
where 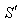 is moving along common X-axis with velocity V with respect to
is moving along common X-axis with velocity V with respect to 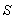 frame. Let the transmitter and receiver be situated at origins
frame. Let the transmitter and receiver be situated at origins 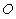 and
and 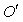 of frames
of frames 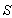 and
and 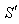 respectively. Let two light signals or pulses be transmitted at time
respectively. Let two light signals or pulses be transmitted at time 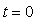 and
and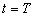 , T being the true period of light pulses. Let
, T being the true period of light pulses. Let 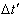 be the interval between the receptions of the pulses by the receiver in the frame
be the interval between the receptions of the pulses by the receiver in the frame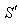 . Since the observer and receiver is at rest in frame
. Since the observer and receiver is at rest in frame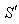 ,
, 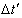 is the proper time interval
is the proper time interval 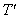 between these pulses. Since the observer continues to be at
between these pulses. Since the observer continues to be at 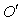 all the time, the distance
all the time, the distance 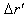 covered by him in the frame
covered by him in the frame 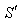 during the reception of the two pulses is zero.Using the inverse Lorentz transformation we can write,
during the reception of the two pulses is zero.Using the inverse Lorentz transformation we can write,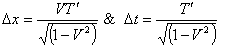 | (29) |
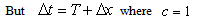 | (30) |
Using the equations (29) and (30) we can write[13]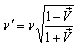 | (31) |
If  and
and 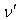 be the actual and observed frequencies of light pulses, respectively .This equation (31) is the formula of the relativistic Doppler’s effect of Special Lorentz transformation for light.
be the actual and observed frequencies of light pulses, respectively .This equation (31) is the formula of the relativistic Doppler’s effect of Special Lorentz transformation for light. 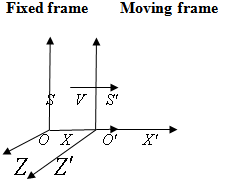 | Figure 3. The frame  is moving along common X-axis with velocity V with respect to is moving along common X-axis with velocity V with respect to  frame frame |
3.2. Relativistic Doppler’s Effect of most General Lorentz Transformation
Consider two frames of references  and
and 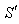 the velocity
the velocity 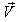 of
of 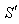 with respect to
with respect to 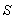 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 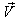 has three components Vx, Vy and Vz. Let the transmitter and receiver be situated at origins
has three components Vx, Vy and Vz. Let the transmitter and receiver be situated at origins 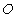 and
and 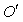 of frames
of frames 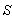 and
and 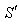 respectively. Let two light signals or pulses be transmitted at time
respectively. Let two light signals or pulses be transmitted at time 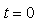 and
and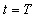 , T being the true period of light pulses. Let
, T being the true period of light pulses. Let 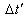 be the interval between the receptions of the pulses by the receiver in the frame
be the interval between the receptions of the pulses by the receiver in the frame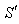 . Since the observer and receiver is at rest in frame
. Since the observer and receiver is at rest in frame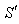 ,
, 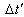 is the proper time interval
is the proper time interval 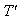 between these pulses. Since the observer continues to be at
between these pulses. Since the observer continues to be at 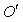 all the time, the distance
all the time, the distance 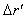 covered by him in the frame
covered by him in the frame 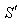 during the reception of the two pulses is zero.
during the reception of the two pulses is zero.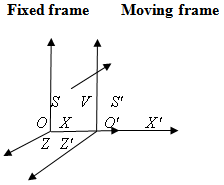 | Figure 4. The frame 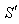 is moving along any arbitrary direction with velocity is moving along any arbitrary direction with velocity 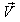 with respect to with respect to 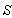 frame frame |
Using the space part and time part of inverse most general Lorentz transformation[2] any one can get the formula of relativistic Doppler’s effect[18] in the most general Lorentz transformation which is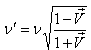 | (32) |
This formula of the relativistic Doppler’s effect coincides with the formula of Special Lorentz transformation
3.3. Relativistic Doppler’s Effect of Mixed Number Lorentz Transformation
Consider the same situation described in Figure 4. Using the similar way of most general Lorentz transformation[2] we can find the formula of Relativistic Doppler’s Effect of mixed number Lorentz transformation[18] which is given by 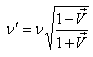 | (33) |
3.4. Relativistic Doppler’s Effect of Quaternion Lorentz Transformation
Consider two frames of references 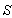 and
and 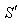 as described in Figure 4. If
as described in Figure 4. If 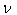 and
and 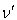 be the actual and observed frequencies of light pulses, respectively, then the formula for the relativistic Doppler’s Effect of quaternion Lorentz transformation[14] can be found as
be the actual and observed frequencies of light pulses, respectively, then the formula for the relativistic Doppler’s Effect of quaternion Lorentz transformation[14] can be found as 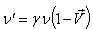 | (34) |
3.5. Relativistic Doppler’s Effect of Geometric Product Lorentz Transformation
Consider two frames of references 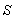 and
and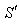 . The velocity
. The velocity 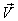 of
of 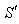 with respect to
with respect to 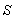 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 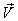 has three components Vx, Vy and Vz. Let the transmitter and receiver be situated at origins
has three components Vx, Vy and Vz. Let the transmitter and receiver be situated at origins 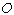 and
and 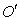 of frames
of frames 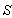 and
and 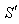 respectively. Let two light signals or pulses be transmitted at time
respectively. Let two light signals or pulses be transmitted at time 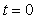 and
and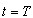 , T being the true period of light pulses. Let
, T being the true period of light pulses. Let 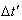 be the interval between the receptions of the pulses by the receiver in the frame
be the interval between the receptions of the pulses by the receiver in the frame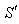 . Since the observer and receiver is at rest in frame
. Since the observer and receiver is at rest in frame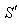 ,
, 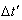 is the proper time interval
is the proper time interval 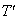 between these pulses. Since the observer continues to be at
between these pulses. Since the observer continues to be at 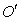 all the time, the distance
all the time, the distance 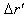 covered by him in the frame
covered by him in the frame 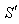 during the reception of the two pulses is zero.Using the space part of the inverse geometric product Lorentz transformation of equation (13)
during the reception of the two pulses is zero.Using the space part of the inverse geometric product Lorentz transformation of equation (13)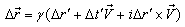 | (35) |
Since  and
and 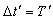 then equation (35) can be written as
then equation (35) can be written as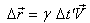 or,
or,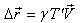 | (36) |
This equation (36) shows the second pulse has to travel this extra distance 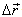 then the first pulse in the frame
then the first pulse in the frame 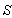 to be able to reach at origin
to be able to reach at origin 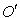 in the moving frame
in the moving frame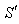 .Using the time part of the geometric product Lorentz transformation of equation (13)
.Using the time part of the geometric product Lorentz transformation of equation (13)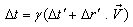 | (37) |
Since 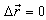 and
and 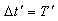 then equation (37) can be written as
then equation (37) can be written as 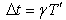 | (38) |
This relation includes both the actual time period T of the pulses and the time taken 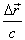 by the second pulse to cover the extra distance
by the second pulse to cover the extra distance 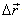 in the frame
in the frame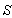 , i.e. Using
, i.e. Using 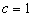 the equation (39) can be written as
the equation (39) can be written as 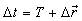 | (40) |
Using (36), (38) and (40) we can write 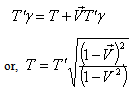 | (41) |
Using equation (23), the equation (41) can be written as 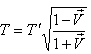 | (42) |
If 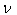 and
and 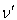 be the actual and observed frequencies of light pulses, respectively, we have
be the actual and observed frequencies of light pulses, respectively, we have 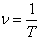 and
and 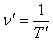 then equation (42) gives
then equation (42) gives 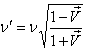 | (43) |
this equation (43) is the formula of the relativistic Doppler’s effect of geometric product Lorentz transformation for light.
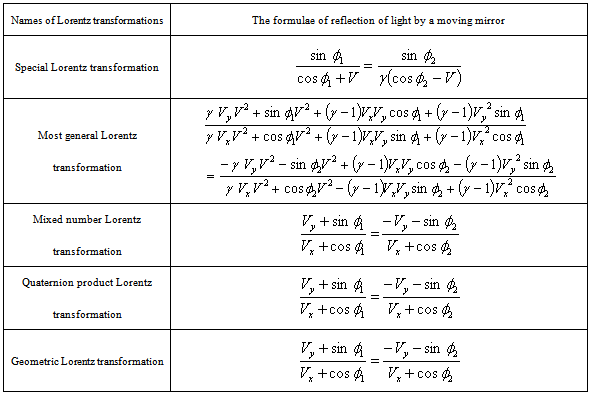
4. Reflection of Light by a moving Mirror
4.1. Reflection of light by a moving mirror in Special Lorentz Transformation
Consider two frames of references 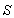 and
and 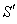 where
where 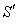 is moving along common X-axis with velocity V with respect to
is moving along common X-axis with velocity V with respect to 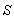 frame. Consider a mirror M to be fixed in the
frame. Consider a mirror M to be fixed in the 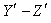 plane of system
plane of system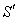 . Consider the mirror is perfectly reflecting, moving along the direction of its normal relative to
. Consider the mirror is perfectly reflecting, moving along the direction of its normal relative to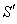 . Let a ray of light in
. Let a ray of light in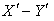 be incident at angle
be incident at angle 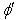 at
at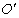 in system
in system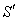 .As mirror M is stationary in system
.As mirror M is stationary in system 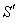 ordinary laws of reflection hold good and so the angle of reflection will be
ordinary laws of reflection hold good and so the angle of reflection will be 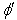 and the reflected ray lies in
and the reflected ray lies in 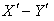 plane. Let the angles of incidence and reflection are measured in system S be
plane. Let the angles of incidence and reflection are measured in system S be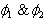 , we get[2]
, we get[2]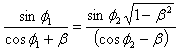 | (44) |
Using 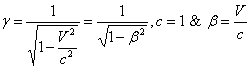 we get from (44)
we get from (44)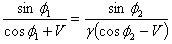 | (45) |
This equation (45) is the law of reflection of light by a moving mirror[2] in the case of special Lorentz transformation
4.2. Reflection of Light by a moving Mirror in Most General Lorentz Transformation
Consider two frames of references 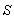 and
and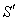 . The velocity
. The velocity 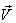 of
of 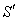 with respect to
with respect to 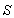 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 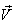 has two components Vx, and Vy . Consider a mirror M to be fixed in the
has two components Vx, and Vy . Consider a mirror M to be fixed in the 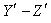 plane of system
plane of system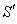 . Consider the mirror is perfectly reflecting, moving along the direction of its normal relative to
. Consider the mirror is perfectly reflecting, moving along the direction of its normal relative to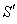 . Let a ray of light in
. Let a ray of light in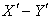 be incident at angle
be incident at angle 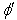 at
at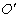 in system
in system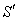 .As mirror M is stationary in system
.As mirror M is stationary in system 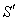 ordinary laws of reflection hold good and so the angle of reflection will be
ordinary laws of reflection hold good and so the angle of reflection will be 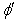 and the reflection ray lies in
and the reflection ray lies in 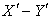 plane .Let the angles of incidence and reflection are measured in system S be
plane .Let the angles of incidence and reflection are measured in system S be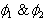 , we get[3]
, we get[3]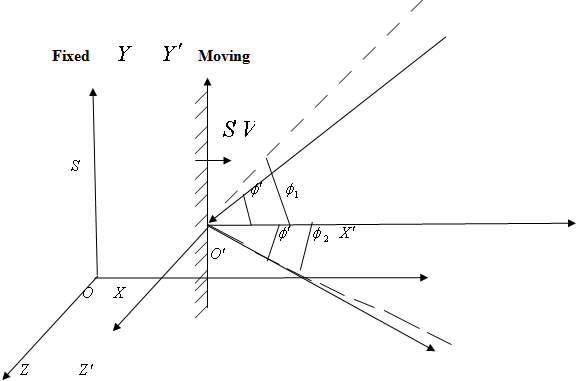 | Figure 5. The reflection of light by a moving mirror where M is fixed in the 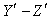 plane of system plane of system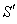 |
Let the incident ray in system 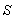 and
and 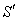 be represented by
be represented by 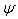 and
and 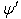 whereand
whereand 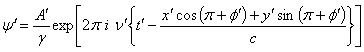 | (47) |
As phase is a Lorenz invariant quantity, using equations (46) and (47) we must have 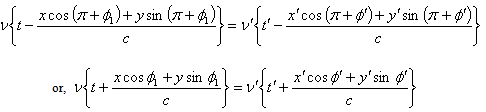 | (48) |
Using 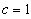 we get from equation (48)
we get from equation (48) 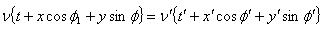 | (49) |
Using equations (3), (4) and (49) and considering the velocity V has two components 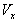 and
and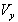 , we can get the formula[19] of the reflection of light ray by a moving mirror in most general Lorentz transformation
, we can get the formula[19] of the reflection of light ray by a moving mirror in most general Lorentz transformation 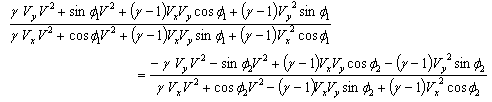
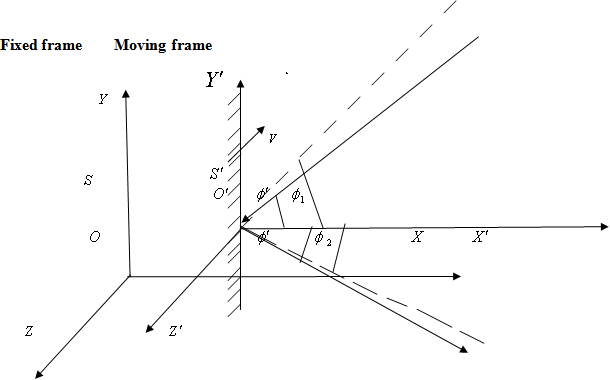 | Figure 6. The frame  is moving along any arbitrary direction with velocity is moving along any arbitrary direction with velocity  with respect to with respect to  frame where a mirror M is fixed in the frame where a mirror M is fixed in the 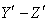 plane of system plane of system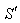 |
4.3. Reflection of Light by a moving Mirror in mixed number Lorentz Transformation
Consider two frames of reference 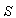 and
and 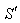 . The velocity
. The velocity 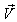 of
of 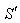 with respect to
with respect to 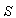 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 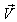 has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (7) and (49) we have considering the velocity V has two components
has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (7) and (49) we have considering the velocity V has two components 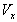 and
and 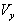
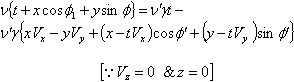 | (50) |
Equating the coefficient of t of equation (50) we get,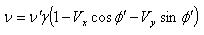 | (51) |
Equating the coefficient of x of equation (50) we get,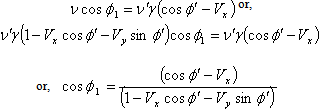 | (52) |
Equating the coefficient of y of equation (50) we get,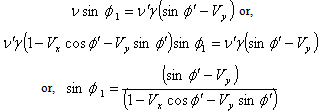 | (53) |
Now from equation (52) and (53) we get,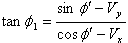 | (54) |
Using equation (8) and (49) we have considering the velocity V has two components 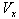 and
and 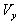
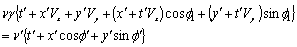 | (55) |
Equating the coefficient of 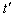 of equation (55) we get,
of equation (55) we get,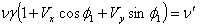 | (56) |
Equating the coefficient of 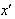 of equation (55) we get,
of equation (55) we get,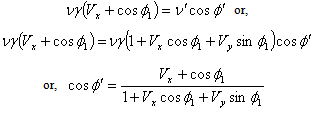 | (57) |
Equating the coefficient of 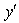 of equation (55) we get,
of equation (55) we get,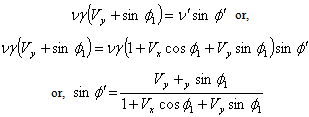 | (58) |
Now from equation (57) and (58) we get,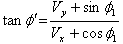 | (59) |
Similarly, for reflected ray the relation between angle of reflection in system 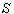 and
and 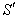 can be obtained as
can be obtained as 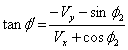 | (60) |
From equation (59) and (60), we get, 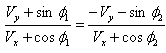 | (61) |
This equation (61) is the law of reflection of light ray by a moving mirror in mixed number Lorentz transformation.
4.4. Reflection of Light by a moving Mirror in Quaternion Lorentz Transformation
Consider two frames of reference 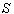 and
and 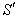 . The velocity
. The velocity 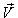 of
of 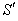 with respect to
with respect to 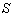 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 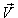 has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (11) and (49) we have considering the velocity V has two components
has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (11) and (49) we have considering the velocity V has two components 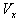 and
and 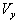 we can get by the similar process of mixed number Lorentz transformation, the same formula for the reflection of light ray by a moving mirror in quaternion Lorentz transformation
we can get by the similar process of mixed number Lorentz transformation, the same formula for the reflection of light ray by a moving mirror in quaternion Lorentz transformation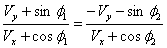 | (62) |
4.5. Reflection of Light by a moving Mirror in Geometric Product Lorentz Transformation
Consider two frames of reference 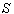 and
and 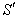 . The velocity
. The velocity 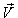 of
of 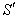 with respect to
with respect to 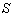 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 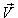 has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (15) and (49), we have considering the velocity V has two components
has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (15) and (49), we have considering the velocity V has two components 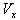 and
and 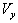 then after a little bit lengthy calculation according to the similar process of mixed number Lorentz transformation we can get the same formula for the reflection of light ray by a moving mirror in geometric product Lorentz transformation
then after a little bit lengthy calculation according to the similar process of mixed number Lorentz transformation we can get the same formula for the reflection of light ray by a moving mirror in geometric product Lorentz transformation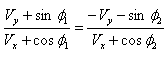 | (63) |
5. Comparison of the Study
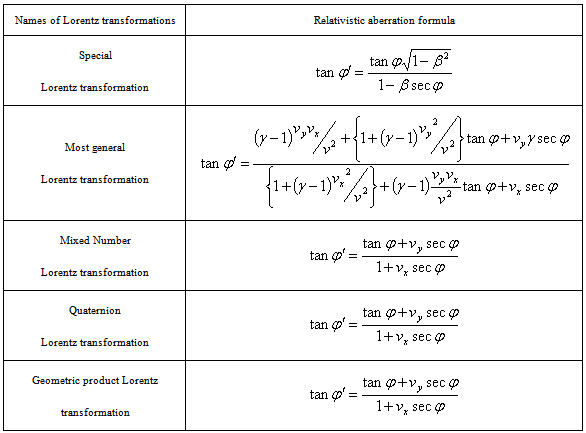
5.1. Comparison of Relativistic Aberrations of Special, Most General, Mixed Number, Quaternion and Geometric Product Lorenz Transformations
5.2. Comparison of Relativistic Doppler’s Effect of Special, Most General, Mixed Number, Quaternion and Geometric Product Lorenz Transformations
5.3. Comparison of the Formulae of the Reflection of Light by a Moving Mirror in Special, Most General, Mixed Number, Quaternion and Geometric Product Lorenz Transformations
6. Conclusions
The Relativistic aberration, Doppler’s effect and the reflection of light ray by a moving mirror formulae of special, most general, mixed number, quaternion and geometric product Lorenz transformations have been derived clearly. We have found that the formulae for Relativistic aberration and for the reflection of light ray by a moving mirror of mixed number, quaternion and geometric product Lorenz transformations are simpler than the formula of most general Lorenz transformation .
References
| [1] | Resnick, R. 1994. Introduction to special relativity, Wiley Eastern limited. |
| [2] | Moller, C. 1972. The Theory of Relativity, Oxford University press, London. |
| [3] | Alam, M.S. 2000. Study of Mixed Number. Proc. Pakistan Acad. of Sci. 37(1): 119-122. |
| [4] | Alam, M.S. 2001. Mixed product of vectors, Journal of Theoretics, 3(4). http://www.journaloftheoretics.com/ |
| [5] | Alam, M.S. 2003. Comparative study of mixed product and quaternion product, Indian J. Physics A 77: 47-49. |
| [6] | Kyrala, A. 1967. Theoretical Physics, W.B. Saunders Company. Philadelphia & London, Toppan Company Limited. Tokyo, Japan. |
| [7] | Alam, M.S. 2003. Different types of product of vectors, NewsBull.Cal.Math.Soc., 26(1,2 & 3) 21-24. |
| [8] | Datta, B.K., De Sabbata V. and Ronchetti L. 1998. Quantization of gravity in real space time, Il Nuovo Cimento, 113B. |
| [9] | Datta, B.K., Datta R. 1998. Einstein field equations in spinor formalism, Foundations of Physics letters, 11,1.. |
| [10] | Md. Shah Alam and Md. Didar Chowdhury, Relativistic Aberration of Mixed number Lorenz Transformation, 2006, Journal of the national Science foundation of Sri Lanka34 (3) |
| [11] | http://mathworld.wolfram.com/Quaternion.html |
| [12] | http://www.cs.appstate.edu/~sjg/class/3110/mathfestalg2000/quaternions1.html |
| [13] | Satya Prokash. Relativistic Mechanics, Pragati Prakashan-2000, India. |
| [14] | Md. Shah Alam and Sabar Bauk, Quaternion Lorenz Transformation, Physics Essays,2011, American Institute of Physics, Canada. |
| [15] | A. Beiser, 1964.The Fundamentals of Physics.Addison-Welsey Publishing,Inc. |
| [16] | A. Beiser, 1995. Concepts of Modern Physics. Mc-Graw-Hill, Inc.Fifth Edition. |
| [17] | Md. Shah Alam and Md. Didar Chowdhury, Study of Relativistic Doppler’s Effect, Proc.Pakistan Acad.Sci.44(2):109-115.2007. |
| [18] | Md. Shah Alam and Md. Didar Chowdhury, Study of reflection of light by a moving mirror,2009,J.Physics.83(2) 233- |

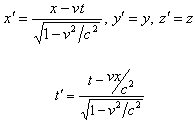
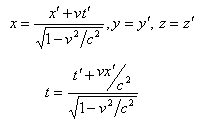
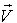 has three components Vx , Vy and Vz , then the relation between the space and time co-ordinates of S and
has three components Vx , Vy and Vz , then the relation between the space and time co-ordinates of S and 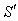 is called the most general Lorentz transformation[2] which can be written as
is called the most general Lorentz transformation[2] which can be written as 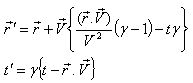
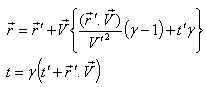
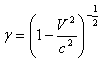 and
and 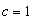
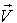 of
of 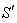 with respect to
with respect to 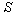 is not along the X-axis; i.e., the velocity
is not along the X-axis; i.e., the velocity 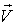 has three components, Vx, Vy, and Vz. Let in this case
has three components, Vx, Vy, and Vz. Let in this case 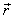 and
and 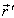 be the space parts in
be the space parts in 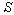 and
and 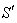 frames, respectively. Then using the mixed product
frames, respectively. Then using the mixed product 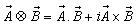 , the mixed number Lorentz transformations[3– 6] can be written as
, the mixed number Lorentz transformations[3– 6] can be written as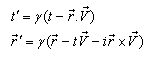
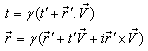
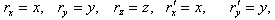
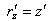 . If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to
. If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to 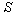 then equation (5) and (6) can be written as
then equation (5) and (6) can be written as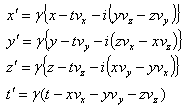
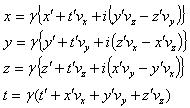
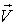 of
of  with respect to
with respect to 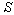 has also three components, Vx, Vy, and Vz as the most general Lorentz transformation. Let in this case
has also three components, Vx, Vy, and Vz as the most general Lorentz transformation. Let in this case 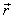 and
and 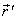 be the space parts in
be the space parts in 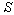 and
and 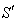 frames respectively. Then using the quaternion product
frames respectively. Then using the quaternion product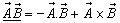 the quaternion Lorentz transformation[7-10] can be written as
the quaternion Lorentz transformation[7-10] can be written as 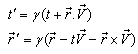
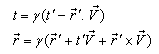
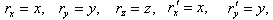
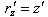 .If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to
.If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to 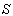 then equation (9) and (10) can be written as
then equation (9) and (10) can be written as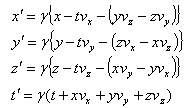
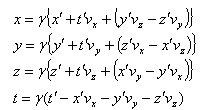
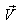 of S' with respect to
of S' with respect to 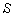 has also three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case
has also three components, Vx, Vy, and Vz as the Most general Lorentz transformation. Let in this case 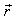 and
and 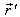 be the space parts in
be the space parts in 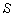 and
and 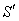 frames respectively. Then using the geometric product of two vectors
frames respectively. Then using the geometric product of two vectors 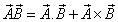 the geometric product Lorentz transformation[11, 12] can be written as
the geometric product Lorentz transformation[11, 12] can be written as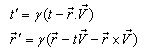
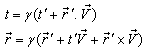
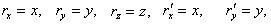
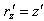 .If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to
.If Vx, Vy, and Vz denote the components of the velocity of the system S' relative to 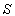 then equation (13) and (14) can be written as
then equation (13) and (14) can be written as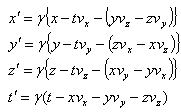
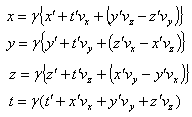
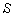 and the earth is in the system
and the earth is in the system 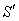 is moving with velocity V relative to the system
is moving with velocity V relative to the system 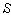 along positive direction of common X-axis. Let the star P observed from the observers
along positive direction of common X-axis. Let the star P observed from the observers 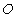 and
and 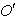 in system
in system 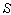 and
and 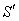 where the frame
where the frame 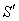 is moving along X-axis with velocity V with respect to
is moving along X-axis with velocity V with respect to 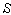 frame. Let the angles made by the light ray in X-Y plane from the star P at any instant in two systems at
frame. Let the angles made by the light ray in X-Y plane from the star P at any instant in two systems at 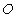 and
and 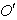 be
be 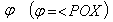 and
and 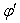
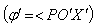 respectively[Figure 1].
respectively[Figure 1].
 and a moving frame
and a moving frame  (the frame
(the frame  is moving along common X-axis with velocity V with respect to
is moving along common X-axis with velocity V with respect to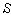 frame)
frame)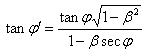 where
where 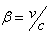
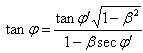
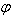 and
and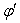 are not same in the two systems; they depend upon the motion of source and observer. Hence equation (17) describes the relativistic aberration of special Lorentz transformation.
are not same in the two systems; they depend upon the motion of source and observer. Hence equation (17) describes the relativistic aberration of special Lorentz transformation.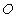 and
and 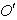 in system
in system 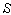 and
and 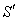 where the frame
where the frame 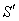 is moving along any arbitrary direction with velocity
is moving along any arbitrary direction with velocity 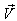 with respect to
with respect to 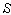 frame as shown in figure -2. Let the angles made by the light ray in X-Y plane from the star P at any instant in two systems at
frame as shown in figure -2. Let the angles made by the light ray in X-Y plane from the star P at any instant in two systems at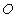 and
and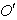 be
be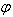
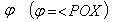 and
and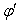
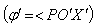 respectively. Here the angle
respectively. Here the angle 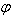 is same in Fig. 1 and 2. But the angle
is same in Fig. 1 and 2. But the angle 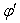 is different Fixed Moving
is different Fixed Moving
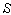 and a moving frame
and a moving frame 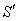 ( the frame
( the frame 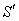 is moving along any arbitrary direction with velocity V with respect to
is moving along any arbitrary direction with velocity V with respect to 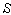 frame)
frame)
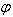 and
and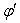 are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (19) gives the relativistic formula for aberration of most general Lorentz transformation.
are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (19) gives the relativistic formula for aberration of most general Lorentz transformation.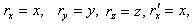
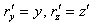 ,then using equation (5) and (6) we can easily find out the aberration formula for two dimension case of the mixed number Lorentz transformation[10]
,then using equation (5) and (6) we can easily find out the aberration formula for two dimension case of the mixed number Lorentz transformation[10]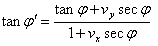
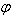 and
and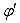 are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (20) gives the relativistic formula for aberration of mixed number Lorentz transformation.
are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (20) gives the relativistic formula for aberration of mixed number Lorentz transformation.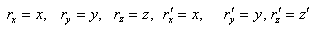 then using equation (9) and (10) we can easily find out the aberration formula for two dimension case of the quaternion Lorentz transformation[14]
then using equation (9) and (10) we can easily find out the aberration formula for two dimension case of the quaternion Lorentz transformation[14]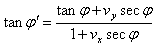
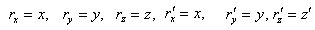 Equation (13) can be written as
Equation (13) can be written as 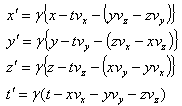
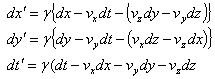 from the above equation we have
from the above equation we have 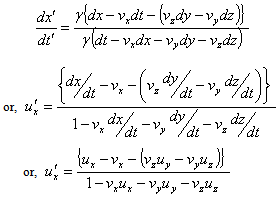
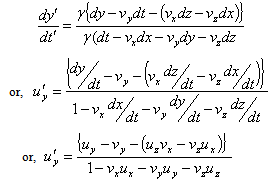
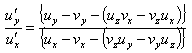 If we consider two dimension case, then we can write
If we consider two dimension case, then we can write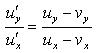
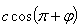 and
and 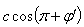 along positive direction of X-axis in system
along positive direction of X-axis in system 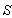 and
and 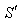 respectively. Also those
respectively. Also those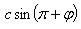 and
and 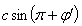 are along positive direction of Y-axis in system
are along positive direction of Y-axis in system 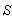 and
and 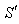 respectively. Thus we have
respectively. Thus we have 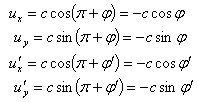
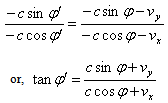 Considering
Considering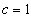 we have
we have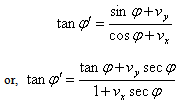
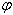 and
and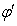 are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (27) gives the relativistic formula for aberration of geometric product Lorentz transformation.
are not same in the two systems. i.e. the direction of light rays depends on the motion of the source emitting light and observer. Equation (27) gives the relativistic formula for aberration of geometric product Lorentz transformation.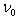 times per second and emits a wave of light with each tick. In the case of observer receding from the light source, the observer travels the distance
times per second and emits a wave of light with each tick. In the case of observer receding from the light source, the observer travels the distance 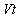 away from the source between the ticks, which mean that the light wave from a given tick takes
away from the source between the ticks, which mean that the light wave from a given tick takes 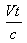 longer to reach him than the previous one. Hence the total time between the arrivals of successive waves is
longer to reach him than the previous one. Hence the total time between the arrivals of successive waves is 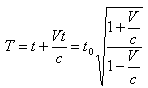 and the observed frequency is
and the observed frequency is 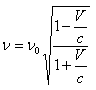 In the case of observer approaching the light source, the observed frequency is
In the case of observer approaching the light source, the observed frequency is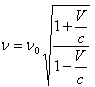
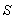 and
and 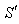 where
where 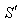 is moving along common X-axis with velocity V with respect to
is moving along common X-axis with velocity V with respect to 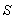 frame. Let the transmitter and receiver be situated at origins
frame. Let the transmitter and receiver be situated at origins 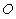 and
and 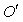 of frames
of frames 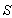 and
and 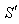 respectively. Let two light signals or pulses be transmitted at time
respectively. Let two light signals or pulses be transmitted at time 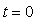 and
and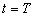 , T being the true period of light pulses. Let
, T being the true period of light pulses. Let 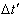 be the interval between the receptions of the pulses by the receiver in the frame
be the interval between the receptions of the pulses by the receiver in the frame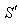 . Since the observer and receiver is at rest in frame
. Since the observer and receiver is at rest in frame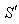 ,
, 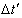 is the proper time interval
is the proper time interval 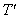 between these pulses. Since the observer continues to be at
between these pulses. Since the observer continues to be at 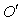 all the time, the distance
all the time, the distance 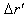 covered by him in the frame
covered by him in the frame 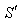 during the reception of the two pulses is zero.Using the inverse Lorentz transformation we can write,
during the reception of the two pulses is zero.Using the inverse Lorentz transformation we can write,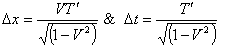
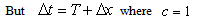
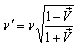
 and
and 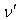 be the actual and observed frequencies of light pulses, respectively .This equation (31) is the formula of the relativistic Doppler’s effect of Special Lorentz transformation for light.
be the actual and observed frequencies of light pulses, respectively .This equation (31) is the formula of the relativistic Doppler’s effect of Special Lorentz transformation for light. 
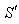 is moving along common X-axis with velocity V with respect to
is moving along common X-axis with velocity V with respect to 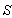 frame
frame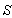 and
and 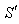 the velocity
the velocity 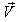 of
of 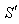 with respect to
with respect to 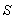 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 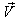 has three components Vx, Vy and Vz. Let the transmitter and receiver be situated at origins
has three components Vx, Vy and Vz. Let the transmitter and receiver be situated at origins 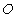 and
and 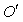 of frames
of frames 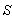 and
and 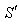 respectively. Let two light signals or pulses be transmitted at time
respectively. Let two light signals or pulses be transmitted at time 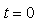 and
and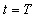 , T being the true period of light pulses. Let
, T being the true period of light pulses. Let 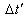 be the interval between the receptions of the pulses by the receiver in the frame
be the interval between the receptions of the pulses by the receiver in the frame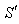 . Since the observer and receiver is at rest in frame
. Since the observer and receiver is at rest in frame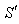 ,
, 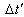 is the proper time interval
is the proper time interval 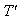 between these pulses. Since the observer continues to be at
between these pulses. Since the observer continues to be at 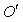 all the time, the distance
all the time, the distance 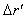 covered by him in the frame
covered by him in the frame 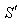 during the reception of the two pulses is zero.
during the reception of the two pulses is zero.
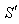 is moving along any arbitrary direction with velocity
is moving along any arbitrary direction with velocity 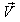 with respect to
with respect to 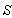 frame
frame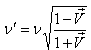
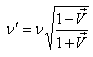
 and
and 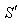 as described in Figure 4. If
as described in Figure 4. If 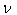 and
and 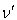 be the actual and observed frequencies of light pulses, respectively, then the formula for the relativistic Doppler’s Effect of quaternion Lorentz transformation[14] can be found as
be the actual and observed frequencies of light pulses, respectively, then the formula for the relativistic Doppler’s Effect of quaternion Lorentz transformation[14] can be found as 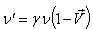
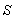 and
and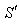 . The velocity
. The velocity 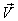 of
of 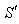 with respect to
with respect to 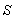 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 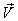 has three components Vx, Vy and Vz. Let the transmitter and receiver be situated at origins
has three components Vx, Vy and Vz. Let the transmitter and receiver be situated at origins 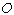 and
and 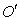 of frames
of frames 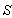 and
and 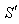 respectively. Let two light signals or pulses be transmitted at time
respectively. Let two light signals or pulses be transmitted at time 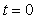 and
and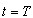 , T being the true period of light pulses. Let
, T being the true period of light pulses. Let 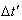 be the interval between the receptions of the pulses by the receiver in the frame
be the interval between the receptions of the pulses by the receiver in the frame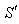 . Since the observer and receiver is at rest in frame
. Since the observer and receiver is at rest in frame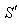 ,
, 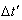 is the proper time interval
is the proper time interval 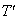 between these pulses. Since the observer continues to be at
between these pulses. Since the observer continues to be at 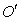 all the time, the distance
all the time, the distance 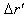 covered by him in the frame
covered by him in the frame 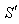 during the reception of the two pulses is zero.Using the space part of the inverse geometric product Lorentz transformation of equation (13)
during the reception of the two pulses is zero.Using the space part of the inverse geometric product Lorentz transformation of equation (13)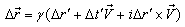
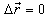 and
and 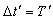 then equation (35) can be written as
then equation (35) can be written as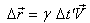 or,
or,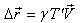
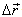 then the first pulse in the frame
then the first pulse in the frame 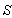 to be able to reach at origin
to be able to reach at origin 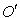 in the moving frame
in the moving frame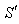 .Using the time part of the geometric product Lorentz transformation of equation (13)
.Using the time part of the geometric product Lorentz transformation of equation (13)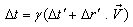
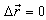 and
and 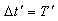 then equation (37) can be written as
then equation (37) can be written as 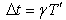
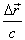 by the second pulse to cover the extra distance
by the second pulse to cover the extra distance 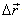 in the frame
in the frame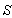 , i.e. Using
, i.e. Using 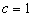 the equation (39) can be written as
the equation (39) can be written as 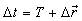
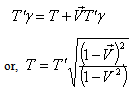
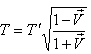
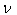 and
and 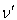 be the actual and observed frequencies of light pulses, respectively, we have
be the actual and observed frequencies of light pulses, respectively, we have 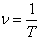 and
and 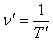 then equation (42) gives
then equation (42) gives 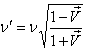
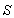 and
and 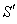 where
where 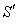 is moving along common X-axis with velocity V with respect to
is moving along common X-axis with velocity V with respect to 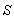 frame. Consider a mirror M to be fixed in the
frame. Consider a mirror M to be fixed in the 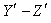 plane of system
plane of system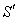 . Consider the mirror is perfectly reflecting, moving along the direction of its normal relative to
. Consider the mirror is perfectly reflecting, moving along the direction of its normal relative to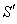 . Let a ray of light in
. Let a ray of light in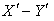 be incident at angle
be incident at angle 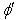 at
at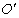 in system
in system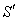 .As mirror M is stationary in system
.As mirror M is stationary in system 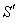 ordinary laws of reflection hold good and so the angle of reflection will be
ordinary laws of reflection hold good and so the angle of reflection will be 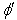 and the reflected ray lies in
and the reflected ray lies in 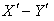 plane. Let the angles of incidence and reflection are measured in system S be
plane. Let the angles of incidence and reflection are measured in system S be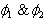 , we get[2]
, we get[2]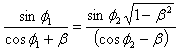
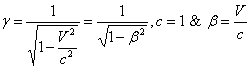 we get from (44)
we get from (44)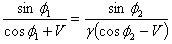
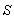 and
and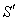 . The velocity
. The velocity 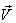 of
of 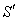 with respect to
with respect to 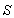 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 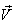 has two components Vx, and Vy . Consider a mirror M to be fixed in the
has two components Vx, and Vy . Consider a mirror M to be fixed in the 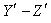 plane of system
plane of system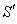 . Consider the mirror is perfectly reflecting, moving along the direction of its normal relative to
. Consider the mirror is perfectly reflecting, moving along the direction of its normal relative to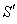 . Let a ray of light in
. Let a ray of light in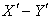 be incident at angle
be incident at angle 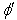 at
at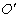 in system
in system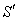 .As mirror M is stationary in system
.As mirror M is stationary in system 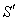 ordinary laws of reflection hold good and so the angle of reflection will be
ordinary laws of reflection hold good and so the angle of reflection will be 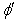 and the reflection ray lies in
and the reflection ray lies in 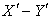 plane .Let the angles of incidence and reflection are measured in system S be
plane .Let the angles of incidence and reflection are measured in system S be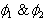 , we get[3]
, we get[3]
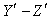 plane of system
plane of system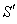
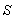 and
and 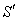 be represented by
be represented by 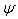 and
and 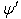 whereand
whereand 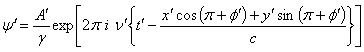
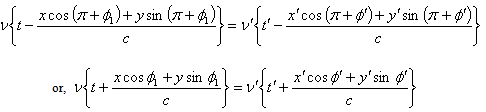
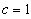 we get from equation (48)
we get from equation (48) 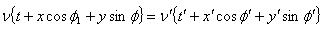
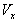 and
and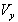 , we can get the formula[19] of the reflection of light ray by a moving mirror in most general Lorentz transformation
, we can get the formula[19] of the reflection of light ray by a moving mirror in most general Lorentz transformation 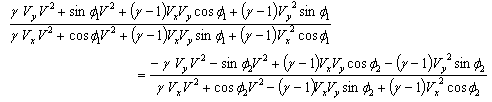

 is moving along any arbitrary direction with velocity
is moving along any arbitrary direction with velocity  with respect to
with respect to  frame where a mirror M is fixed in the
frame where a mirror M is fixed in the 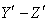 plane of system
plane of system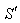
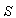 and
and 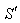 . The velocity
. The velocity 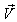 of
of 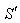 with respect to
with respect to 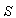 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 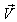 has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (7) and (49) we have considering the velocity V has two components
has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (7) and (49) we have considering the velocity V has two components 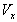 and
and 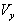
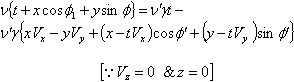
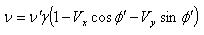
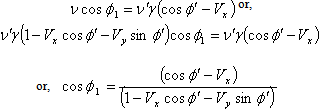
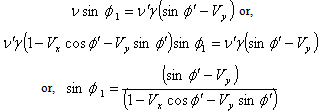
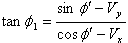
 and
and 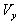
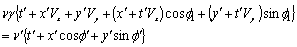
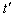 of equation (55) we get,
of equation (55) we get,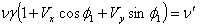
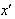 of equation (55) we get,
of equation (55) we get,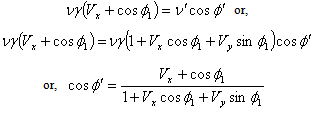
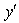 of equation (55) we get,
of equation (55) we get,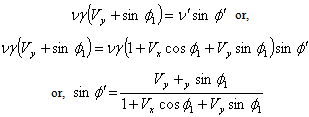
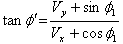
 and
and  can be obtained as
can be obtained as 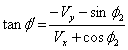
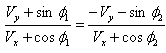
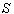 and
and 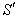 . The velocity
. The velocity 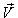 of
of 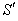 with respect to
with respect to 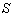 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 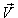 has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (11) and (49) we have considering the velocity V has two components
has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (11) and (49) we have considering the velocity V has two components 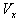 and
and 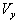 we can get by the similar process of mixed number Lorentz transformation, the same formula for the reflection of light ray by a moving mirror in quaternion Lorentz transformation
we can get by the similar process of mixed number Lorentz transformation, the same formula for the reflection of light ray by a moving mirror in quaternion Lorentz transformation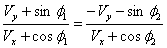
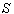 and
and 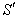 . The velocity
. The velocity 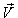 of
of 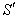 with respect to
with respect to 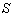 is not along X-axis i.e. the velocity
is not along X-axis i.e. the velocity 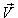 has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (15) and (49), we have considering the velocity V has two components
has three components Vx, Vy and Vz. Consider same situation as described in the Figure 6.Using equation (15) and (49), we have considering the velocity V has two components 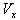 and
and 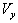 then after a little bit lengthy calculation according to the similar process of mixed number Lorentz transformation we can get the same formula for the reflection of light ray by a moving mirror in geometric product Lorentz transformation
then after a little bit lengthy calculation according to the similar process of mixed number Lorentz transformation we can get the same formula for the reflection of light ray by a moving mirror in geometric product Lorentz transformation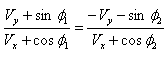



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML