J. I. Mbegbu 1, C. O. Todo 2
1Department of Mathematics, University of Benin, Benin City, Nigeria
2Department of Statistics, School of Computing and IT, Delta State Polytechnic, Otefe-Oghara, Nigeria
Correspondence to: J. I. Mbegbu , Department of Mathematics, University of Benin, Benin City, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We constructed an 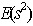 -optimal supersaturated design (SSD) with an experimental run-size, n = 20 and number of factors, m = 57 (multiple of 19). The construction is based on balanced incomplete block designs using a theorem proposed by Bulutoglu and Cheng. This is achieved by constructing the initial blocks of the balanced incomplete block design using the theorem. Consequently, all other blocks are generated to constitute a balanced incomplete block design (BIBD),and the complete blocks that constitute the BIBD is transformed into the required supersaturated design( SSD).
-optimal supersaturated design (SSD) with an experimental run-size, n = 20 and number of factors, m = 57 (multiple of 19). The construction is based on balanced incomplete block designs using a theorem proposed by Bulutoglu and Cheng. This is achieved by constructing the initial blocks of the balanced incomplete block design using the theorem. Consequently, all other blocks are generated to constitute a balanced incomplete block design (BIBD),and the complete blocks that constitute the BIBD is transformed into the required supersaturated design( SSD).
Keywords:
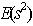 -Optimal, Supersaturated, Design Matrix, Incomplete Block Designs, Run-Size
-Optimal, Supersaturated, Design Matrix, Incomplete Block Designs, Run-Size
1. Introduction
Consider a two-level experimental design with n experimental runs and m factors. A two-level experimental design is called a supersaturated design(SSD) if m>n-1. According to[7], the analysis of supersaturated designs rely on the effect of sparsity principle in which the number of important factors is relatively small.In[11], the 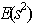 criterion is considered as the most popular criterion, and it measures the average correlation among the columns of the design matrix of an SSD. Suppose we have a design with n runs and m factors, and each of the factors has 2 levels, then
criterion is considered as the most popular criterion, and it measures the average correlation among the columns of the design matrix of an SSD. Suppose we have a design with n runs and m factors, and each of the factors has 2 levels, then 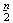 of the entries in each column have values +1, and others -1 respectively. Let X denotes the
of the entries in each column have values +1, and others -1 respectively. Let X denotes the 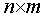 design matrix . Hence,
design matrix . Hence,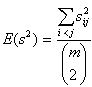 | (1.1) |
where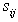 denotes the element in the ith row and jth column of
denotes the element in the ith row and jth column of 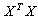 .For the supersaturated design with n runs and m factors, each column of the design matrix contains the same number of 1’s and -1’s. The number of possible factors, m that could be accommodated satisfies the inequality
.For the supersaturated design with n runs and m factors, each column of the design matrix contains the same number of 1’s and -1’s. The number of possible factors, m that could be accommodated satisfies the inequality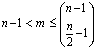 | (1.2) |
[8] showed that when n is even: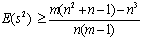 | (1.3) |
According to[7], the lower bound (1.3) is attainable when n is a multiple of 4 and m is a multiple of 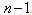 , or
, or  (mod 4) or m is an even multiple of
(mod 4) or m is an even multiple of 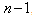 .Moreover,[6] and[8] independently derived the lower bound:
.Moreover,[6] and[8] independently derived the lower bound: 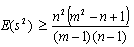 | (1.4) |
for any supersaturated design with m factors and n runs.[1] proposed the 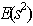 criterion for constructing two-level supersaturated designs, and[8] based the construction of supersaturated designs on combining q Hadamard matrices. This means that a simple construction of an SSD is to piece together q balanced incomplete balanced block designs( BIBD’s)
criterion for constructing two-level supersaturated designs, and[8] based the construction of supersaturated designs on combining q Hadamard matrices. This means that a simple construction of an SSD is to piece together q balanced incomplete balanced block designs( BIBD’s) 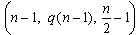 . Thus, the resulting SSD will have distinct blocks.[9] presented a method of using difference family to construct BIBD’s
. Thus, the resulting SSD will have distinct blocks.[9] presented a method of using difference family to construct BIBD’s 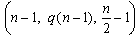 with distinct blocks, and from such a BIBD one could easily construct an
with distinct blocks, and from such a BIBD one could easily construct an 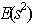 -optimal SSD. [10] introduced the construction of SSD’s that satisfy specified lower bounds of
-optimal SSD. [10] introduced the construction of SSD’s that satisfy specified lower bounds of 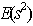 ,and[12] highlighted ways of constructing optimal mix-level supersaturated designs. In[4], a column wise-pairwise algorithm for constructing SSD’s is discussed.In this study, we shall construct an
,and[12] highlighted ways of constructing optimal mix-level supersaturated designs. In[4], a column wise-pairwise algorithm for constructing SSD’s is discussed.In this study, we shall construct an 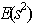 -optimal supersaturated design (SSD) with an even run-size, n, and number of factors, a multiple of
-optimal supersaturated design (SSD) with an even run-size, n, and number of factors, a multiple of 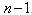 .
.
2. Materials and Method
Theorem[2]: Suppose 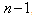 is an odd prime power,
is an odd prime power, 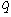 an even divisor of
an even divisor of 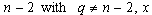 a primitive element of
a primitive element of 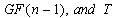 a subset of
a subset of 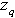 of size
of size 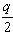 . Let e be the smallest positive integer such that . Then, the
. Let e be the smallest positive integer such that . Then, the 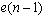 sets:
sets: 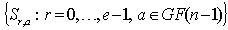 , where
, where 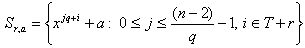 are distinct and constitute a BIBD
are distinct and constitute a BIBD 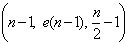 .Furthermore, if
.Furthermore, if 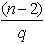 is odd, and
is odd, and 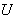 a subset of
a subset of 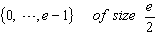 such that
such that 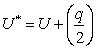 , where
, where 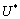 is the complement of
is the complement of 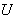 in and the addition is reduced modulo
in and the addition is reduced modulo 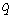 , then the
, then the 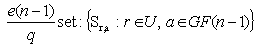 constitutes a BIBD with distinct blocks. The theorem satisfies the lower bound (1.4), and shall be used in the construction of the supersaturated design (SSD). The construction of the SSD will be based on BIBD, which is more general and flexible[6].According to[2], given a Hadamard matrix of order n, there exists a BIBD
constitutes a BIBD with distinct blocks. The theorem satisfies the lower bound (1.4), and shall be used in the construction of the supersaturated design (SSD). The construction of the SSD will be based on BIBD, which is more general and flexible[6].According to[2], given a Hadamard matrix of order n, there exists a BIBD 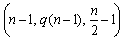 for every
for every 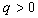 .The following definitions shall be used in this work.Definition 1: Let
.The following definitions shall be used in this work.Definition 1: Let 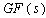 denotes a finite field with s elements. An element in a group within a finite field from which other elements are obtained is called a generator of the group. The generator of a group is called a primitive element of the field. Definition 2: Let
denotes a finite field with s elements. An element in a group within a finite field from which other elements are obtained is called a generator of the group. The generator of a group is called a primitive element of the field. Definition 2: Let 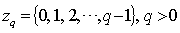 . Multiplication and addition in
. Multiplication and addition in 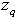 are in reduced modulo
are in reduced modulo 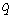 . Now, for each subset
. Now, for each subset 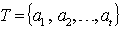 of
of 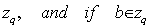 ,then
,then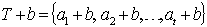 .Definition 3: According to[5], an incomplete block design
.Definition 3: According to[5], an incomplete block design  is called a balanced incomplete block design (BIBD) if(i) each block contains k different treatments (ii) each treatment appears in r blocks, that is, each treatment is replicated r times.(iii) every pair of treatments appears within blocks exactly
is called a balanced incomplete block design (BIBD) if(i) each block contains k different treatments (ii) each treatment appears in r blocks, that is, each treatment is replicated r times.(iii) every pair of treatments appears within blocks exactly 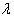 times.For a BIBD, according to[3](a)
times.For a BIBD, according to[3](a) 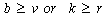 (b)
(b) 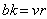 (c) :
(c) : 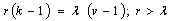 Definition 4: We define a BIBD by its incidence matrix
Definition 4: We define a BIBD by its incidence matrix 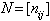 , where
, where 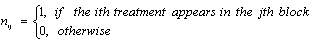 Construction of an
Construction of an 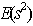 -Optimal Supersaturated Design: Let the primitive element
-Optimal Supersaturated Design: Let the primitive element 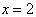 . Then, we shall construct a BIBD (19, 57, 9) in the following way:Let the value of integer
. Then, we shall construct a BIBD (19, 57, 9) in the following way:Let the value of integer 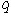 in the theorem be 6.
in the theorem be 6. 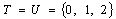 since T is a subset of
since T is a subset of 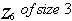 . There are many of such subsets of sizes 3 within
. There are many of such subsets of sizes 3 within 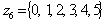 . The number of subsets of sizes 3 in
. The number of subsets of sizes 3 in 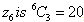 . The 20 subsets of
. The 20 subsets of 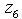 each of size 3 are: {0, 1, 2}, {0, 1, 3}, {0, 1,4}, {0, 1, 5}, {0, 2, 3}, {0, 2, 4}, {0, 2, 5}, {0, 3, 4}, {0, 3, 5}, {0, 4, 5}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, {3, 4, 5}.Hence, T + e = T + 3=T for all these subsets except {0, 1, 2}. For the subset {0, 1, 2},
each of size 3 are: {0, 1, 2}, {0, 1, 3}, {0, 1,4}, {0, 1, 5}, {0, 2, 3}, {0, 2, 4}, {0, 2, 5}, {0, 3, 4}, {0, 3, 5}, {0, 4, 5}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, {3, 4, 5}.Hence, T + e = T + 3=T for all these subsets except {0, 1, 2}. For the subset {0, 1, 2}, 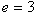 .We now obtain the initial blocks of the BIBD as follows: For
.We now obtain the initial blocks of the BIBD as follows: For 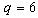 , by the Theorem :
, by the Theorem :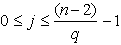 which reduces to
which reduces to 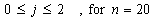 .Since,
.Since, 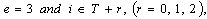 then
then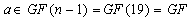 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18).Considering the set;
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18).Considering the set; 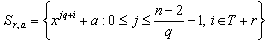 , and evaluating
, and evaluating 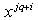 , for
, for 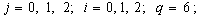
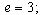
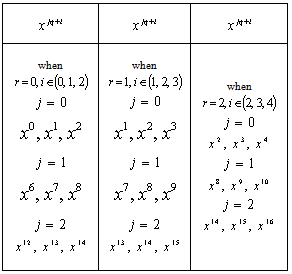
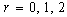 , we obtain Table 1 .
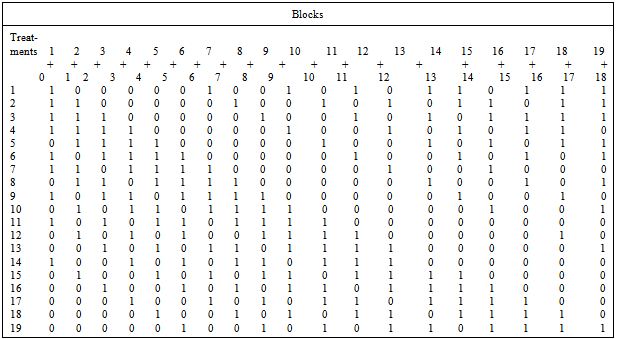
, we obtain Table 1 .Table 1. Blocks
 |
| |
|
3. Results and Discussion
With the primitive element , Table 1 contains three initial blocks namely, {20, 21, 22, 26, 27, 28, 212, 213, 214}, {21, 22, 23, 27, 28, 29, 213, 214, 215}and {22, 23, 24, 28, 29, 210, 214, 215, 216}. As multiplication is in reduced modulo , i.e., reduced modulo 19, the first initial block contains: {20, 21, 22, 26, 27, 28, 212, 213, 214}, where 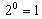 ,
, 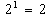 ,
, 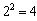 ,
,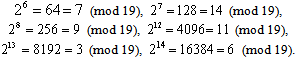 Therefore, the first initial block (FIB) is {1, 2, 4, 7, 14, 9, 11, 6}From Table 1, the second initial block (SIB) contains: {21, 22, 23, 27, 28, 29, 213, 214, 215}, where
Therefore, the first initial block (FIB) is {1, 2, 4, 7, 14, 9, 11, 6}From Table 1, the second initial block (SIB) contains: {21, 22, 23, 27, 28, 29, 213, 214, 215}, where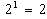 ,
, 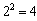 ,
, 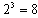 ,
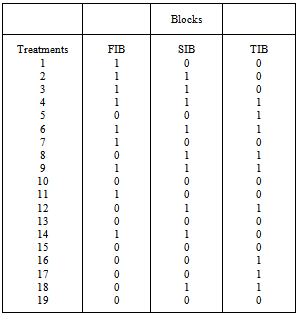
,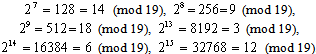 Therefore, the second initial block is {2, 4, 8, 14, 9, 18, 3, 6, 12}When the above procedure is repeated for the third initial block, we have the third initial block (TIB) as {4, 8, 16, 9, 18, 17, 6, 12, 5}.We note that in the three initial blocks, the numbers indicate the treatments that occur in each block. In this case, the three initial blocks are shown in Table 2 .
Therefore, the second initial block is {2, 4, 8, 14, 9, 18, 3, 6, 12}When the above procedure is repeated for the third initial block, we have the third initial block (TIB) as {4, 8, 16, 9, 18, 17, 6, 12, 5}.We note that in the three initial blocks, the numbers indicate the treatments that occur in each block. In this case, the three initial blocks are shown in Table 2 .Table 2. The Three Initial Blocks
 |
| |
|
Now, consider 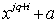 , where
, where 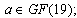 that is, adding the integers 0, 1, . . . ,18 (mod 19) to all the elements in the three initial blocks produces a BIBD with 57 distinct blocks each of size 9 and 19 blocks. From the First Initial Blocks: FIB + 0 = {1, 2, 4, 7, 14, 9, 11, 3, 6},FIB +1 = {2, 3, 5, 8, 15, 10, 12, 4, 7},FIB + 2 = {3, 4, 6, 9, 16, 11, 13, 5, 8}, FIB + 3 = {4, 5, 7, 10, 17, 12, 14, 6, 9},FIB + 4 = {5, 6, 8, 11, 18, 13, 15, 7, 10},FIB + 5 = {6, 7, 9, 12, 19, 14, 16, 8, 11},FIB + 6 = {7, 8, 10, 13, 1, 15, 17, 9, 12},FIB + 7 = {8, 9, 11, 14, 2, 16, 18, 10, 13},FIB + 8 = {9, 10, 12, 15, 3, 17, 19, 11, 14},FIB + 9 = {10, 11, 13, 16, 4, 18, 1, 12, 15},FIB + 10 = {11, 12, 14, 17, 5, 19, 2, 13, 16},FIB + 11 = {12, 13, 15, 18, 6, 1, 3, 14, 17},FIB + 12 = {13, 14, 16, 19, 7, 2, 4, 15, 18},FIB + 13 = {14, 15, 17, 1, 8, 3, 5, 16, 19},FIB + 14 = {15, 16, 18, 2, 9, 4, 6, 17, 1},FIB + 15 = {16, 17, 19, 3, 10, 5, 7, 18, 2},FIB + 16 = {17, 18, 1, 4, 11, 6, 8, 19, 3},FIB + 17 = {18, 19, 2, 5, 12, 7, 9, 1, 4},FIB + 18 = {19, 1, 3, 6, 13, 8, 10, 2, 5}.The above procedure is repeated on the Second Initial Block and the Third Initial Block respectively, altogether gives the BIBD (19, 57, 9). The First 19 blocks of the BIBD (19, 57, 9) obtained from the First Initial Block are shown in Table 3 below .Adopting the BIBD(19, 57, 9), we obtain a 19 x 57 treatment-block incidence matrix for BIBD(19, 57, 9). Using SSD(n, m) = SSD(n, e(n-1)), we obtain an SSD(20, 57) from the BIBD(19, 57, 9) by converting all 0’s in the incidence matrix of the BIBD(19, 57, 9) to -1’s and adding a first row of all 1’s to the treatment-block incidence matrix. This gives an
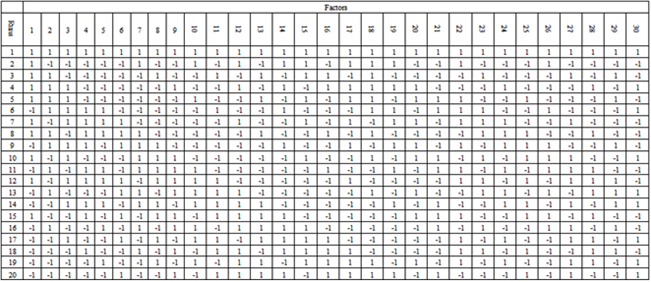
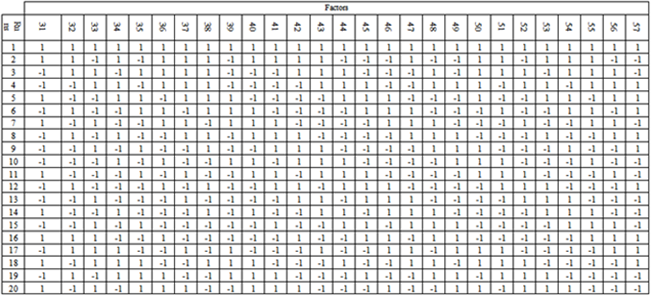
that is, adding the integers 0, 1, . . . ,18 (mod 19) to all the elements in the three initial blocks produces a BIBD with 57 distinct blocks each of size 9 and 19 blocks. From the First Initial Blocks: FIB + 0 = {1, 2, 4, 7, 14, 9, 11, 3, 6},FIB +1 = {2, 3, 5, 8, 15, 10, 12, 4, 7},FIB + 2 = {3, 4, 6, 9, 16, 11, 13, 5, 8}, FIB + 3 = {4, 5, 7, 10, 17, 12, 14, 6, 9},FIB + 4 = {5, 6, 8, 11, 18, 13, 15, 7, 10},FIB + 5 = {6, 7, 9, 12, 19, 14, 16, 8, 11},FIB + 6 = {7, 8, 10, 13, 1, 15, 17, 9, 12},FIB + 7 = {8, 9, 11, 14, 2, 16, 18, 10, 13},FIB + 8 = {9, 10, 12, 15, 3, 17, 19, 11, 14},FIB + 9 = {10, 11, 13, 16, 4, 18, 1, 12, 15},FIB + 10 = {11, 12, 14, 17, 5, 19, 2, 13, 16},FIB + 11 = {12, 13, 15, 18, 6, 1, 3, 14, 17},FIB + 12 = {13, 14, 16, 19, 7, 2, 4, 15, 18},FIB + 13 = {14, 15, 17, 1, 8, 3, 5, 16, 19},FIB + 14 = {15, 16, 18, 2, 9, 4, 6, 17, 1},FIB + 15 = {16, 17, 19, 3, 10, 5, 7, 18, 2},FIB + 16 = {17, 18, 1, 4, 11, 6, 8, 19, 3},FIB + 17 = {18, 19, 2, 5, 12, 7, 9, 1, 4},FIB + 18 = {19, 1, 3, 6, 13, 8, 10, 2, 5}.The above procedure is repeated on the Second Initial Block and the Third Initial Block respectively, altogether gives the BIBD (19, 57, 9). The First 19 blocks of the BIBD (19, 57, 9) obtained from the First Initial Block are shown in Table 3 below .Adopting the BIBD(19, 57, 9), we obtain a 19 x 57 treatment-block incidence matrix for BIBD(19, 57, 9). Using SSD(n, m) = SSD(n, e(n-1)), we obtain an SSD(20, 57) from the BIBD(19, 57, 9) by converting all 0’s in the incidence matrix of the BIBD(19, 57, 9) to -1’s and adding a first row of all 1’s to the treatment-block incidence matrix. This gives an 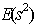 -optimal 20-run SSD for 57 factors shown in Table 4 below.Table 4 shows the complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9). We observe that all the two level factors occur in the higher level for the first run (run 1) of the design. Table 4 shows the complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9). We observe that all the two level factors occur in the higher level for the first run (run 1) of the design.
-optimal 20-run SSD for 57 factors shown in Table 4 below.Table 4 shows the complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9). We observe that all the two level factors occur in the higher level for the first run (run 1) of the design. Table 4 shows the complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9). We observe that all the two level factors occur in the higher level for the first run (run 1) of the design. Table 3. First 19 blocks of the BIBD (19, 57, 9) obtained from the first initial block
 |
| |
|
Table 4. The complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9)
 |
| |
|
Table 4. Cont’d
 |
| |
|
4. Conclusions
Using the primitive element of the field, GF(s) as defined in the work of[2], we constructed a supersaturated design, SSD(20, 57) with 57 factors and 20 experimental runs. We determine the 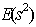 -value for the SSD(20, 57) as 40.31 which satisfies the
-value for the SSD(20, 57) as 40.31 which satisfies the 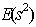 lower bound proposed by[8]. This guarantees the validity of design, SSD(20, 57). In the literature, a number of E(s2)-optimal supersaturated design construction techniques have been utilised, but oftentimes, most are very rigorous, not adaptable and flexible. In this respect, constructing an E(s2)-optimal supersaturated design from balanced incomplete block design excels. All the details of this construction technique have been successfully demonstrated in this paper. Obviously, this technique would be of great aid in the search for more E(s2)-optimal supersaturated designs for factors screening in the preliminary stage of industrial or scientific experiments.
lower bound proposed by[8]. This guarantees the validity of design, SSD(20, 57). In the literature, a number of E(s2)-optimal supersaturated design construction techniques have been utilised, but oftentimes, most are very rigorous, not adaptable and flexible. In this respect, constructing an E(s2)-optimal supersaturated design from balanced incomplete block design excels. All the details of this construction technique have been successfully demonstrated in this paper. Obviously, this technique would be of great aid in the search for more E(s2)-optimal supersaturated designs for factors screening in the preliminary stage of industrial or scientific experiments.
References
| [1] | Booth, K. H. and Cox, D. R. (1962), “Some Systematic Supersaturated Designs”, Technometrics, Vol. 4, 489-495. |
| [2] | Bulutoglu, D. A. and Cheng, C. (2004), “Construction of 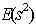 -optimal Supersaturated Designs”, The Annals of Statistics, Vol.32, No.4, August ,2004. -optimal Supersaturated Designs”, The Annals of Statistics, Vol.32, No.4, August ,2004. |
| [3] | Fisher, R. A. (1940), “An Examination of Different Possible Solutions of a Problem in Incomplete Blocks”, Annals of Eugenics, Vol. 10. pp. 52-57. |
| [4] | Li, W. W. and Wu, C. F. J, (1997), “Columnwise-Pairwise Algorithm with Applications to the Construction of Supersaturated Designs”, Technometrics, Vol. 39: pp. 171-179 MR 1452345. |
| [5] | Mbegbu, J. I. (2007). “Optimal Balanced Incomplete Block Designs with Cost Constraints”, A PhD Thesis, Rivers State University of Science and Technology, Port-Harcourt, Nigeria. |
| [6] | Nguyen, N. K. (1996). “An Algorithmic Approach to Constructing Supersaturated Designs”, Technometrics, Vol. 38 pp. 67-73. |
| [7] | Nguyen, N. K. and Cheng-Shul (2008), “New E(s2)-Optimal Supersaturated Designs Constructed from Incomplete Block Designs”, Technometrics, February 2008, Vol. 50, No. 1. |
| [8] | Tang, B. X. and Wu, C. F. J. (1997), “A Method for Constructing Supersaturated Designs and its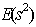 -Optimality”, Canadian Journal of Statistics, Vol. 25, pp. 191-201. -Optimality”, Canadian Journal of Statistics, Vol. 25, pp. 191-201. |
| [9] | Wilson, R. M. (1972), “Cyclotomy and Difference Families is Elementary Abelian Groups”, Journal of Number Theory, Vol. 4, pp. 17-47. |
| [10] | Wu, C. F. J. (1993), “Construction of Supersaturated Design Through Partially AliasedInteractions”, Biometrika,, Vol. 80, pp. 661-669. MR 1248029. Methpdol. 63 621-632 MR 1858407. |
| [11] | Xu, H. and Wu, C. F. J. (2005), “Construction of Optimal Multi-level Supersaturated Designs” ,The Annals of Statistics, Vol. 33, No. 6. Dec. 2005. |
| [12] | Sun,Fasheng; Lin,K J Dennis; and Liu,Min-Qian(2011),”On the Construction of Optimal Mix-Level Supersaturated Designs”, Annals of Statistics,Vol.39, No.2,pp1310-1333. |

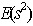 -optimal supersaturated design (SSD) with an experimental run-size, n = 20 and number of factors, m = 57 (multiple of 19). The construction is based on balanced incomplete block designs using a theorem proposed by Bulutoglu and Cheng. This is achieved by constructing the initial blocks of the balanced incomplete block design using the theorem. Consequently, all other blocks are generated to constitute a balanced incomplete block design (BIBD),and the complete blocks that constitute the BIBD is transformed into the required supersaturated design( SSD).
-optimal supersaturated design (SSD) with an experimental run-size, n = 20 and number of factors, m = 57 (multiple of 19). The construction is based on balanced incomplete block designs using a theorem proposed by Bulutoglu and Cheng. This is achieved by constructing the initial blocks of the balanced incomplete block design using the theorem. Consequently, all other blocks are generated to constitute a balanced incomplete block design (BIBD),and the complete blocks that constitute the BIBD is transformed into the required supersaturated design( SSD).
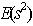 -Optimal, Supersaturated, Design Matrix, Incomplete Block Designs, Run-Size
-Optimal, Supersaturated, Design Matrix, Incomplete Block Designs, Run-Size
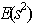 criterion is considered as the most popular criterion, and it measures the average correlation among the columns of the design matrix of an SSD. Suppose we have a design with n runs and m factors, and each of the factors has 2 levels, then
criterion is considered as the most popular criterion, and it measures the average correlation among the columns of the design matrix of an SSD. Suppose we have a design with n runs and m factors, and each of the factors has 2 levels, then 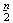 of the entries in each column have values +1, and others -1 respectively. Let X denotes the
of the entries in each column have values +1, and others -1 respectively. Let X denotes the 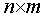 design matrix . Hence,
design matrix . Hence,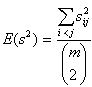
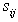 denotes the element in the ith row and jth column of
denotes the element in the ith row and jth column of 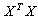 .For the supersaturated design with n runs and m factors, each column of the design matrix contains the same number of 1’s and -1’s. The number of possible factors, m that could be accommodated satisfies the inequality
.For the supersaturated design with n runs and m factors, each column of the design matrix contains the same number of 1’s and -1’s. The number of possible factors, m that could be accommodated satisfies the inequality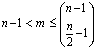
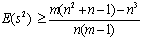
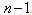 , or
, or 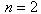 (mod 4) or m is an even multiple of
(mod 4) or m is an even multiple of 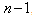 .Moreover,[6] and[8] independently derived the lower bound:
.Moreover,[6] and[8] independently derived the lower bound: 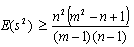
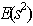 criterion for constructing two-level supersaturated designs, and[8] based the construction of supersaturated designs on combining q Hadamard matrices. This means that a simple construction of an SSD is to piece together q balanced incomplete balanced block designs( BIBD’s)
criterion for constructing two-level supersaturated designs, and[8] based the construction of supersaturated designs on combining q Hadamard matrices. This means that a simple construction of an SSD is to piece together q balanced incomplete balanced block designs( BIBD’s) 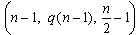 . Thus, the resulting SSD will have distinct blocks.[9] presented a method of using difference family to construct BIBD’s
. Thus, the resulting SSD will have distinct blocks.[9] presented a method of using difference family to construct BIBD’s 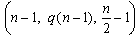 with distinct blocks, and from such a BIBD one could easily construct an
with distinct blocks, and from such a BIBD one could easily construct an 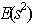 -optimal SSD. [10] introduced the construction of SSD’s that satisfy specified lower bounds of
-optimal SSD. [10] introduced the construction of SSD’s that satisfy specified lower bounds of 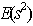 ,and[12] highlighted ways of constructing optimal mix-level supersaturated designs. In[4], a column wise-pairwise algorithm for constructing SSD’s is discussed.In this study, we shall construct an
,and[12] highlighted ways of constructing optimal mix-level supersaturated designs. In[4], a column wise-pairwise algorithm for constructing SSD’s is discussed.In this study, we shall construct an 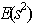 -optimal supersaturated design (SSD) with an even run-size, n, and number of factors, a multiple of
-optimal supersaturated design (SSD) with an even run-size, n, and number of factors, a multiple of 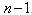 .
.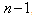 is an odd prime power,
is an odd prime power, 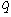 an even divisor of
an even divisor of 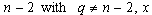 a primitive element of
a primitive element of 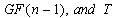 a subset of
a subset of 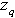 of size
of size 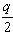 . Let e be the smallest positive integer such that . Then, the
. Let e be the smallest positive integer such that . Then, the 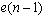 sets:
sets: 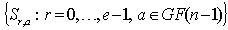 , where
, where 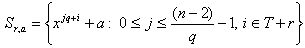 are distinct and constitute a BIBD
are distinct and constitute a BIBD 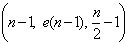 .Furthermore, if
.Furthermore, if 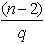 is odd, and
is odd, and 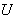 a subset of
a subset of 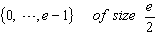 such that
such that 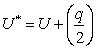 , where
, where 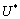 is the complement of
is the complement of 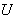 in and the addition is reduced modulo
in and the addition is reduced modulo 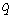 , then the
, then the 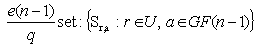 constitutes a BIBD with distinct blocks. The theorem satisfies the lower bound (1.4), and shall be used in the construction of the supersaturated design (SSD). The construction of the SSD will be based on BIBD, which is more general and flexible[6].According to[2], given a Hadamard matrix of order n, there exists a BIBD
constitutes a BIBD with distinct blocks. The theorem satisfies the lower bound (1.4), and shall be used in the construction of the supersaturated design (SSD). The construction of the SSD will be based on BIBD, which is more general and flexible[6].According to[2], given a Hadamard matrix of order n, there exists a BIBD 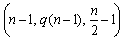 for every
for every 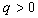 .The following definitions shall be used in this work.Definition 1: Let
.The following definitions shall be used in this work.Definition 1: Let 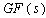 denotes a finite field with s elements. An element in a group within a finite field from which other elements are obtained is called a generator of the group. The generator of a group is called a primitive element of the field. Definition 2: Let
denotes a finite field with s elements. An element in a group within a finite field from which other elements are obtained is called a generator of the group. The generator of a group is called a primitive element of the field. Definition 2: Let 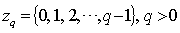 . Multiplication and addition in
. Multiplication and addition in 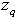 are in reduced modulo
are in reduced modulo 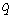 . Now, for each subset
. Now, for each subset 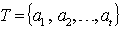 of
of 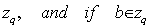 ,then
,then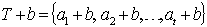 .Definition 3: According to[5], an incomplete block design
.Definition 3: According to[5], an incomplete block design  is called a balanced incomplete block design (BIBD) if(i) each block contains k different treatments (ii) each treatment appears in r blocks, that is, each treatment is replicated r times.(iii) every pair of treatments appears within blocks exactly
is called a balanced incomplete block design (BIBD) if(i) each block contains k different treatments (ii) each treatment appears in r blocks, that is, each treatment is replicated r times.(iii) every pair of treatments appears within blocks exactly 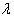 times.For a BIBD, according to[3](a)
times.For a BIBD, according to[3](a) 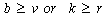 (b)
(b) 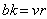 (c) :
(c) : 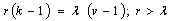 Definition 4: We define a BIBD by its incidence matrix
Definition 4: We define a BIBD by its incidence matrix 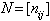 , where
, where 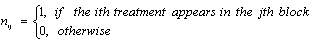 Construction of an
Construction of an 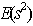 -Optimal Supersaturated Design: Let the primitive element
-Optimal Supersaturated Design: Let the primitive element 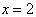 . Then, we shall construct a BIBD (19, 57, 9) in the following way:Let the value of integer
. Then, we shall construct a BIBD (19, 57, 9) in the following way:Let the value of integer 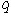 in the theorem be 6.
in the theorem be 6. 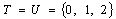 since T is a subset of
since T is a subset of 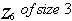 . There are many of such subsets of sizes 3 within
. There are many of such subsets of sizes 3 within 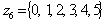 . The number of subsets of sizes 3 in
. The number of subsets of sizes 3 in 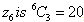 . The 20 subsets of
. The 20 subsets of 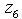 each of size 3 are: {0, 1, 2}, {0, 1, 3}, {0, 1,4}, {0, 1, 5}, {0, 2, 3}, {0, 2, 4}, {0, 2, 5}, {0, 3, 4}, {0, 3, 5}, {0, 4, 5}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, {3, 4, 5}.Hence, T + e = T + 3=T for all these subsets except {0, 1, 2}. For the subset {0, 1, 2},
each of size 3 are: {0, 1, 2}, {0, 1, 3}, {0, 1,4}, {0, 1, 5}, {0, 2, 3}, {0, 2, 4}, {0, 2, 5}, {0, 3, 4}, {0, 3, 5}, {0, 4, 5}, {1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, {3, 4, 5}.Hence, T + e = T + 3=T for all these subsets except {0, 1, 2}. For the subset {0, 1, 2}, 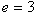 .We now obtain the initial blocks of the BIBD as follows: For
.We now obtain the initial blocks of the BIBD as follows: For 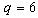 , by the Theorem :
, by the Theorem :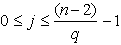 which reduces to
which reduces to 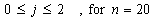 .Since,
.Since, 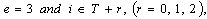 then
then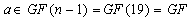 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18).Considering the set;
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18).Considering the set; 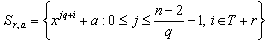 , and evaluating
, and evaluating 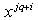 , for
, for 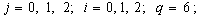
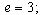
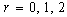 , we obtain Table 1 .
, we obtain Table 1 .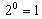 ,
, 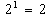 ,
, 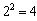 ,
,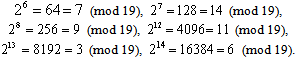 Therefore, the first initial block (FIB) is {1, 2, 4, 7, 14, 9, 11, 6}From Table 1, the second initial block (SIB) contains: {21, 22, 23, 27, 28, 29, 213, 214, 215}, where
Therefore, the first initial block (FIB) is {1, 2, 4, 7, 14, 9, 11, 6}From Table 1, the second initial block (SIB) contains: {21, 22, 23, 27, 28, 29, 213, 214, 215}, where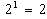 ,
, 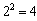 ,
, 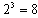 ,
,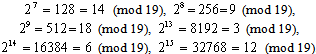 Therefore, the second initial block is {2, 4, 8, 14, 9, 18, 3, 6, 12}When the above procedure is repeated for the third initial block, we have the third initial block (TIB) as {4, 8, 16, 9, 18, 17, 6, 12, 5}.We note that in the three initial blocks, the numbers indicate the treatments that occur in each block. In this case, the three initial blocks are shown in Table 2 .
Therefore, the second initial block is {2, 4, 8, 14, 9, 18, 3, 6, 12}When the above procedure is repeated for the third initial block, we have the third initial block (TIB) as {4, 8, 16, 9, 18, 17, 6, 12, 5}.We note that in the three initial blocks, the numbers indicate the treatments that occur in each block. In this case, the three initial blocks are shown in Table 2 . , where
, where 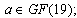 that is, adding the integers 0, 1, . . . ,18 (mod 19) to all the elements in the three initial blocks produces a BIBD with 57 distinct blocks each of size 9 and 19 blocks. From the First Initial Blocks: FIB + 0 = {1, 2, 4, 7, 14, 9, 11, 3, 6},FIB +1 = {2, 3, 5, 8, 15, 10, 12, 4, 7},FIB + 2 = {3, 4, 6, 9, 16, 11, 13, 5, 8}, FIB + 3 = {4, 5, 7, 10, 17, 12, 14, 6, 9},FIB + 4 = {5, 6, 8, 11, 18, 13, 15, 7, 10},FIB + 5 = {6, 7, 9, 12, 19, 14, 16, 8, 11},FIB + 6 = {7, 8, 10, 13, 1, 15, 17, 9, 12},FIB + 7 = {8, 9, 11, 14, 2, 16, 18, 10, 13},FIB + 8 = {9, 10, 12, 15, 3, 17, 19, 11, 14},FIB + 9 = {10, 11, 13, 16, 4, 18, 1, 12, 15},FIB + 10 = {11, 12, 14, 17, 5, 19, 2, 13, 16},FIB + 11 = {12, 13, 15, 18, 6, 1, 3, 14, 17},FIB + 12 = {13, 14, 16, 19, 7, 2, 4, 15, 18},FIB + 13 = {14, 15, 17, 1, 8, 3, 5, 16, 19},FIB + 14 = {15, 16, 18, 2, 9, 4, 6, 17, 1},FIB + 15 = {16, 17, 19, 3, 10, 5, 7, 18, 2},FIB + 16 = {17, 18, 1, 4, 11, 6, 8, 19, 3},FIB + 17 = {18, 19, 2, 5, 12, 7, 9, 1, 4},FIB + 18 = {19, 1, 3, 6, 13, 8, 10, 2, 5}.The above procedure is repeated on the Second Initial Block and the Third Initial Block respectively, altogether gives the BIBD (19, 57, 9). The First 19 blocks of the BIBD (19, 57, 9) obtained from the First Initial Block are shown in Table 3 below .Adopting the BIBD(19, 57, 9), we obtain a 19 x 57 treatment-block incidence matrix for BIBD(19, 57, 9). Using SSD(n, m) = SSD(n, e(n-1)), we obtain an SSD(20, 57) from the BIBD(19, 57, 9) by converting all 0’s in the incidence matrix of the BIBD(19, 57, 9) to -1’s and adding a first row of all 1’s to the treatment-block incidence matrix. This gives an
that is, adding the integers 0, 1, . . . ,18 (mod 19) to all the elements in the three initial blocks produces a BIBD with 57 distinct blocks each of size 9 and 19 blocks. From the First Initial Blocks: FIB + 0 = {1, 2, 4, 7, 14, 9, 11, 3, 6},FIB +1 = {2, 3, 5, 8, 15, 10, 12, 4, 7},FIB + 2 = {3, 4, 6, 9, 16, 11, 13, 5, 8}, FIB + 3 = {4, 5, 7, 10, 17, 12, 14, 6, 9},FIB + 4 = {5, 6, 8, 11, 18, 13, 15, 7, 10},FIB + 5 = {6, 7, 9, 12, 19, 14, 16, 8, 11},FIB + 6 = {7, 8, 10, 13, 1, 15, 17, 9, 12},FIB + 7 = {8, 9, 11, 14, 2, 16, 18, 10, 13},FIB + 8 = {9, 10, 12, 15, 3, 17, 19, 11, 14},FIB + 9 = {10, 11, 13, 16, 4, 18, 1, 12, 15},FIB + 10 = {11, 12, 14, 17, 5, 19, 2, 13, 16},FIB + 11 = {12, 13, 15, 18, 6, 1, 3, 14, 17},FIB + 12 = {13, 14, 16, 19, 7, 2, 4, 15, 18},FIB + 13 = {14, 15, 17, 1, 8, 3, 5, 16, 19},FIB + 14 = {15, 16, 18, 2, 9, 4, 6, 17, 1},FIB + 15 = {16, 17, 19, 3, 10, 5, 7, 18, 2},FIB + 16 = {17, 18, 1, 4, 11, 6, 8, 19, 3},FIB + 17 = {18, 19, 2, 5, 12, 7, 9, 1, 4},FIB + 18 = {19, 1, 3, 6, 13, 8, 10, 2, 5}.The above procedure is repeated on the Second Initial Block and the Third Initial Block respectively, altogether gives the BIBD (19, 57, 9). The First 19 blocks of the BIBD (19, 57, 9) obtained from the First Initial Block are shown in Table 3 below .Adopting the BIBD(19, 57, 9), we obtain a 19 x 57 treatment-block incidence matrix for BIBD(19, 57, 9). Using SSD(n, m) = SSD(n, e(n-1)), we obtain an SSD(20, 57) from the BIBD(19, 57, 9) by converting all 0’s in the incidence matrix of the BIBD(19, 57, 9) to -1’s and adding a first row of all 1’s to the treatment-block incidence matrix. This gives an 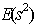 -optimal 20-run SSD for 57 factors shown in Table 4 below.Table 4 shows the complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9). We observe that all the two level factors occur in the higher level for the first run (run 1) of the design. Table 4 shows the complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9). We observe that all the two level factors occur in the higher level for the first run (run 1) of the design.
-optimal 20-run SSD for 57 factors shown in Table 4 below.Table 4 shows the complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9). We observe that all the two level factors occur in the higher level for the first run (run 1) of the design. Table 4 shows the complete 57 factors of the SSD(20, 57) constructed from the BIBD(19, 57, 9). We observe that all the two level factors occur in the higher level for the first run (run 1) of the design. 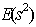 -value for the SSD(20, 57) as 40.31 which satisfies the
-value for the SSD(20, 57) as 40.31 which satisfies the 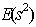 lower bound proposed by[8]. This guarantees the validity of design, SSD(20, 57). In the literature, a number of E(s2)-optimal supersaturated design construction techniques have been utilised, but oftentimes, most are very rigorous, not adaptable and flexible. In this respect, constructing an E(s2)-optimal supersaturated design from balanced incomplete block design excels. All the details of this construction technique have been successfully demonstrated in this paper. Obviously, this technique would be of great aid in the search for more E(s2)-optimal supersaturated designs for factors screening in the preliminary stage of industrial or scientific experiments.
lower bound proposed by[8]. This guarantees the validity of design, SSD(20, 57). In the literature, a number of E(s2)-optimal supersaturated design construction techniques have been utilised, but oftentimes, most are very rigorous, not adaptable and flexible. In this respect, constructing an E(s2)-optimal supersaturated design from balanced incomplete block design excels. All the details of this construction technique have been successfully demonstrated in this paper. Obviously, this technique would be of great aid in the search for more E(s2)-optimal supersaturated designs for factors screening in the preliminary stage of industrial or scientific experiments. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML




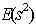 -optimal Supersaturated Designs”, The Annals of Statistics, Vol.32, No.4, August ,2004.
-optimal Supersaturated Designs”, The Annals of Statistics, Vol.32, No.4, August ,2004.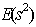 -Optimality”, Canadian Journal of Statistics, Vol. 25, pp. 191-201.
-Optimality”, Canadian Journal of Statistics, Vol. 25, pp. 191-201.