Ibrahim Yusuf , Nafiu Hussaini
Department of Mathematical Sciences, Faculty of Science, Bayero University, Kano
Correspondence to: Ibrahim Yusuf , Department of Mathematical Sciences, Faculty of Science, Bayero University, Kano.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Many authors have studied the effectiveness of a redundant system under two or three types of failure under the assumption that such failures are repairable. Little attention is paid on whether such repair action can restore the system operating condition to as good as new (perfect repair) and the effect of such perfect repair on the system performance. In this study, various measures of system effectiveness such as mean time to system failure (MTSF), steady state availability, busy period and profit function of a 2-out-of-3 repairable system with perfect repair are analyzed using Kolmogorov’s forward equation method. Some particular cases have been discussed graphically. The results have indicated that perfect repair action plays a vital role on system performance. Simulations results show that perfect repair is important particularly in increasing mean time to system failure, availability and system performance as a whole.
Keywords:
Mean Time To System Failure (MTSF), Availability, Profit, Redundancy, Perfect Repair, Kolmogorov’s Equation Method, 2-Out-Of-3 Standby System
1. Introduction
Redundancy is a technique used to improve system reliability and availability. Reliability is vital for proper utilization and maintenance of any system. It involves technique for increasing system effectiveness through reducing failure frequency and maintenance costminimization. One of the forms of redundancy is the k-out-of-n system which finds wide application in industrial system. Redundancy, repair action (perfect), and preventive maintenance are some of the ways by which the reliability of a system can be improved. K-out-of-n systems are often encountered industrial applications. Electronics industry, telecommunication network systems, power generator and transmission systems are the common examples ofk-out-of-n systems. In general, there are three types in standby, i.e. cold, hot and warm standby. A lot of papers dealing with the reliability and availability of k-out-of-n systems (standby systems) have been published.[3] discussed cost analysis of k-out–of-n: G system with active standby redundancy components and repair facility,[2] studied the cost analysis of a two unit cold standby redundant system with two types of unit failure involving common cause failure,[1] deals with cost analysis of a two unit cold standby redundant system with two types of failure and preventive maintenance,[4] studied profit analysis of a two unit cold standby system with preventive maintenance,[6] deals with stochastic analysis of a redundant system involving common human failure,[5] deals with the evaluation of reliability and availability characteristics of different system.[7] studied cost analysis of series systems with cold standby components and a repairable service station, Bhatti et al[8], considered two identical unit cold standby systems with single repairman. Kumar et al[9] analyzed cost benefit analysis of a two unit system in which units work in parallel and become degraded after repair, Gupta el al[10] deals with stochastic analysis of a two non identical unit standby model. The system consist priority unit (p) and ordinary unit (o). A single repair facility appears and disappears from the system randomly with constant rates, Malik et al[11] analyzed two reliability models for a system of non identical units original and duplicate using regenerative point technique., Mahmoud and Moshrefa[12] deal with the study of the stochastic analysis of a two unit cold standby system considering hardware failure, human error failure and preventive maintenance, Yusuf and Bala[13], studied stochastic two models of two unit parallel system. In model I, the system can be normal, deterioration (slow, mild or fast deterioration), failure whereas in model II, the system can either be in normal of failure modes. Using linear first order linear differential equations, various measures of system effectiveness such as mean time to system failure (MTSF) and availability are obtained to see the effect of deterioration on such measures, Kumar and Kadyan[14] deal with profit analysis of two unit non identical system with degradation and replacement while Sureria et al[15] studied cost benefit analysis of a computer system with priority to software replacement over hardware repair.
1.1. Objectives
Many authors studied redundant system exposes to different failure types. However, such systems are subject to different types of repairs like as bad as old, imperfect repair, worse repair, worst repair meaning that in course of time their condition falls from higher to lower, and subsequently fail. However some repairs (perfect) can restore the system operating condition to as good as new The question raise here is whether such perfect repairs can affect some measures of system effectiveness like mean time to system failure (MTSF) and system availability. The purpose of the present paper is to discuss reliability and availability evaluation of 2-out-of-3 system under perfect repair condition. The system is failed if two of its units failed. The system is analyzed using Kolmogorov’s equations method. Graphs are plotted to highlight important results.Notations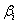 Constant type
Constant type 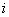 failure rate
failure rate 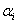 Constant type
Constant type 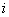 repair rate
repair rate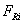 Failed unit under type
Failed unit under type 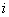 repair
repair 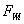 Failed unit waiting for type
Failed unit waiting for type 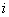 repair
repair  S Unit in Standby O Unit in operationAssumptions1. The system consist of 3 components/units2. Initially two units are in operable condition of full capacity3. The system is failed when the number of working component goes down below 24. Failure and repair time follow exponential distribution5. Repair is as good as new(Perfect repair).
S Unit in Standby O Unit in operationAssumptions1. The system consist of 3 components/units2. Initially two units are in operable condition of full capacity3. The system is failed when the number of working component goes down below 24. Failure and repair time follow exponential distribution5. Repair is as good as new(Perfect repair).
2. Method
State of the SystemFig. 1 Schematic diagram of the system ,
,  ,
,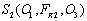 ,
, 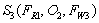 ,
,  ,
, ,
, 
2.1. Mean Time to System Failure Analysis
From Fig. 1 above, define 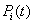 to be the probability that the system at time
to be the probability that the system at time 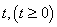 is in state
is in state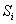 . Let
. Let  be the probability row vector at time
be the probability row vector at time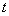 , the initial condition for this paper are
, the initial condition for this paper are  | Figure 1. Schematic diagram of the system |
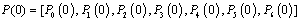
 we obtain the following differential equations:
we obtain the following differential equations: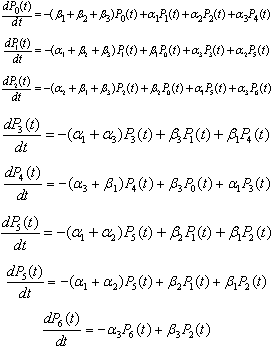 | (1) |
the system of differential equations can be written in matrix as form as 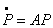 Where
Where It is difficult to evaluate the transient solutions hence following[3,4,7] we delete the rows and columns of absorbing state of matrix
It is difficult to evaluate the transient solutions hence following[3,4,7] we delete the rows and columns of absorbing state of matrix  and take the transpose to produce a new matrix, say
and take the transpose to produce a new matrix, say . The expected time to reach an absorbing state is obtained from
. The expected time to reach an absorbing state is obtained from 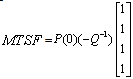 | (2) |
Where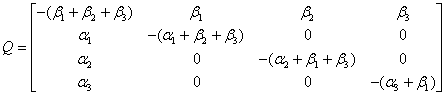 The steady state mean time to system failure is:
The steady state mean time to system failure is: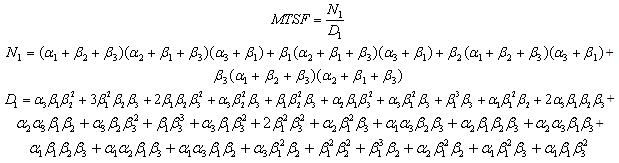
2.2. Availability Analysis
For the analysis of availability case of Fig. 1 using the same initial conditions for this problem as 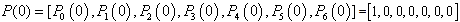 The differential equations can be expressed as
The differential equations can be expressed as The steady-state availability is given by
The steady-state availability is given by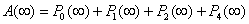 | (3) |
In the steady state, the derivatives of the state probabilities become zero so that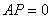 | (4) |
which in matrix form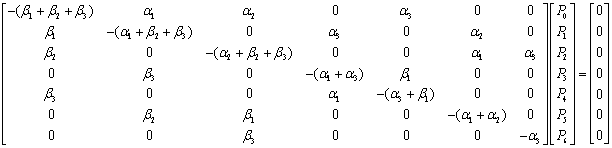 Using the following normalizing condition
Using the following normalizing condition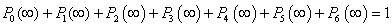 | (5) |
We substitute (5) in any of the redundant rows in (4) to give 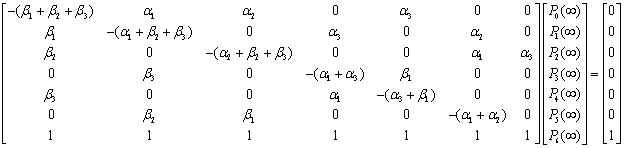 We solve for the system of equations in the matrix above to obtain the steady-state probabilities
We solve for the system of equations in the matrix above to obtain the steady-state probabilities 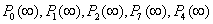 The steady-state availability is given by
The steady-state availability is given by 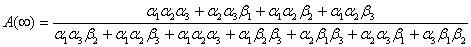
2.3. Busy Period Analysis
Using the same initial condition as for the reliability case: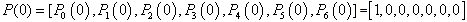 The differential equations can be expressed as
The differential equations can be expressed as 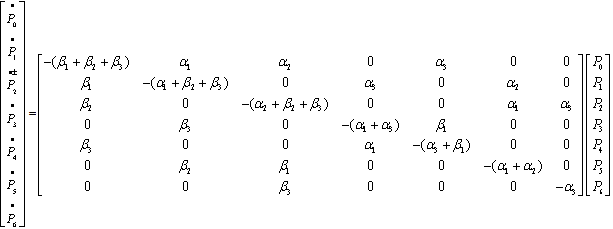 In the steady state, the derivatives of the state probabilities become zero and this will enable us to compute steady state busy :
In the steady state, the derivatives of the state probabilities become zero and this will enable us to compute steady state busy : | (6) |
and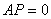 , which in matrix form
, which in matrix form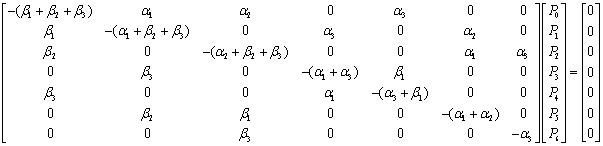 We solve for
We solve for  Using the following normalizing condition
Using the following normalizing condition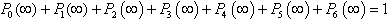 | (7) |
We substitute (7) in any of the redundant rows in (4) to give  The steady state busy period
The steady state busy period  is therefore
is therefore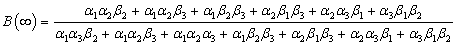
2.4. Profit analysis
Following[1,3]the expected profit per unit time incurred to the system in the steady-state is given by:Profit =total revenue from system using - total cost due to repair | (8) |
Where PF: is the profit incurred to the systemR: is the revenue per unit up time of the system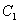 : is the cost per unit time which the system is under repair
: is the cost per unit time which the system is under repair
3. Results
Fig. 2: shows relation between type I repair rate and MTSF of the system Fig. 3: shows relation between type I repair rate and availability of the system Fig. 4: shows the relation between type I repair rate and profit function of the system Table 1: shows the relation between type I repair rate and the profit of the system .
4. Discussion and Conclusions
4.1. Discussion
For the study of system behavior, we plot graphs in Fig. 2 to 4 for MTSF, system availability and profit function with respect to  while other parameters are kept fixed as
while other parameters are kept fixed as 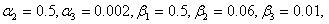
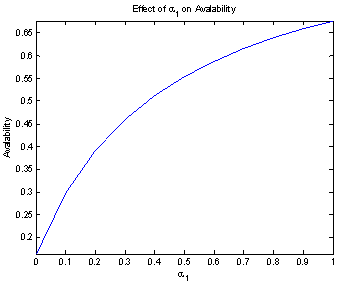
 ,From Fig. 2 it is clear that MTSF increases with increase in the value of which reflects the effect of perfect repair on MTSF. From Fig. 3 the system availability increases with increase in the value of
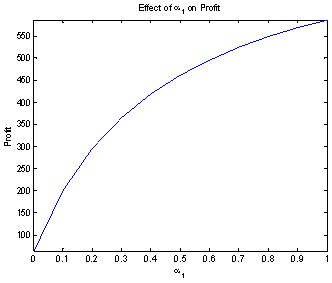
,From Fig. 2 it is clear that MTSF increases with increase in the value of which reflects the effect of perfect repair on MTSF. From Fig. 3 the system availability increases with increase in the value of  . Thus, the more the repair is perfect, the more the system is available for operation. In Fig. 4 it can be observed that with increase in the value of
. Thus, the more the repair is perfect, the more the system is available for operation. In Fig. 4 it can be observed that with increase in the value of 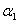 the profit also increase. Thus, the more the system is in perfect condition the more it is effective. Same argument can also be observe in table 1 where increase in the value of
the profit also increase. Thus, the more the system is in perfect condition the more it is effective. Same argument can also be observe in table 1 where increase in the value of 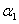 lead to the increase in profit function.
lead to the increase in profit function.| Table 1. Relation between type I repair rate and the profit |
| | α1 | Profit | | 0 | 63.40 | | 0.1 | 200.64 | | 0.2 | 296.00 | | 0.3 | 366.12 | | 0.4 | 419.83 | | 0.5 | 462.31 | | 0.6 | 496.73 | | 0.7 | 525.19 | | 0.8 | 549.12 | | 0.9 | 569.52 | | 1 | 587.12 |
|
|
 | Figure 3. effect of type I repair rate on system availability |
 | Figure 4. effect of type I repair rate on profit function |
4.2. Conclusions
In this study, we developed the explicit expressions for MTSF, system availability, busy period and profit function for 2-out-of-3 system subjected to perfect repair. Graphs were plotted to show the effect of perfect repair on important measures of system effectiveness. Simulations results show that perfect repair is important particularly in increasing mean time to system failure, availability, and profit function and system performance as a whole.
References
| [1] | El-Said, K.M.,. ( 2008).Cost analysis of a system with preventive maintenance by using Kolmogorov’s forward equations method. Ame. J. of App. Sci. 5(4), 405-410 |
| [2] | Haggag, M.Y., (2009). Cost analysis of a system involving common cause failures and preventive maintenance.J. Maths. And Stat. 5(4), 305-310 |
| [3] | Haggag, M.Y., (2009). Cost analysis of k-out-of-n repairable system with dependent failure and stand by support using kolmogorov’s forward equations method. J. Maths. And Stat. 5(4), 401-407 |
| [4] | El-Said, K.M., and M.S. El-Sherbeny. ( 2005).Profit analysis of a two unit cold standby system with preventive maintenance and random change in units. J. Maths and Stat.,1 (1) 71-77 |
| [5] | El-Said, K.M., and M.S. El-Sherbeny. (2005) .Evaluation of reliability and availability characteristics of two different systems by using linear first order differential equations. J. Maths and Stat.,1 (2) 119-123 |
| [6] | Gupta., R. and Mittal., M. (2006). Stochastic analysis of a compound redundant system involving human failure. J. Maths and Stat. 2 (3), pp 407-413. |
| [7] | Wang, K., Hseih, C., and Liou, C. H. (2006). Cost benefit analysis of series systems with cold standby components and a repairable service station. Quality technology and quantitative management. Vol. 3(1), pp 77-92. |
| [8] | Bhatti, J., Chitkara, A., and Bhardwaj, N., (2011). Profit analysis of two unit cold standby system with two types of failures under inspection policy and discreet distribution. International Journal of science and engineering research, Vol.2 (2), pp 1-7. |
| [9] | Kumar, Jitender., Kadyan, M.S. and Malik, S.C., (2010). Cost benefit analysis of a two unit parallel system subject to degradation after repair. Applied mathematical sciences, 4(56), pp 2749-2758. |
| [10] | Gupta, R., Goel, C.K. and Tomer, A. (2010). Analysis of a two unit standby system with correlated failure and repair nd random appearance and disappearance of repairman. |
| [11] | Malik, S.C., Bharwaj, R.K. and Grewal, A.S. (2010). Probabilistic analysis of a system of two non identical parallel units with priority to repair to repair subject to inspection. Journal of reliability and statistical studies, vol. 3(1), pp 1-11 |
| [12] | Mahmoud, M.A.W. and Moshref, M.E. (2010). On a two unit cold standby system considering hardware, human error failures and preventive maintenance, Mathematics and Computer modeling, 51(5-6), pp 736-745. |
| [13] | Yusuf, I. and Bala, S.I. (2012). Stochastic modeling of a two unit parallel system under two types of failures. International Journal of Latest trends in Mathematics, Vol. 2 (1), pp 44-53 |
| [14] | Kumar, J. and Kadyan, M.S. (2012). Profit analysis of a system of non identical units with degradation and replacement. International journal of computer application, vol. 40 (3), pp 19-25 |
| [15] | Sureria, J.K., Malik, S.C. and Anand, J. (2012). Cost benefit analysis of a computer system with priority to software replacement over hardware repair. Applied Mathematical Sciences, vol. 6 (75), pp 3723-3734. |

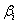 Constant type
Constant type 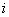 failure rate
failure rate 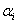 Constant type
Constant type 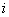 repair rate
repair rate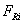 Failed unit under type
Failed unit under type 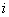 repair
repair 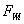 Failed unit waiting for type
Failed unit waiting for type 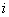 repair
repair  S Unit in Standby O Unit in operationAssumptions1. The system consist of 3 components/units2. Initially two units are in operable condition of full capacity3. The system is failed when the number of working component goes down below 24. Failure and repair time follow exponential distribution5. Repair is as good as new(Perfect repair).
S Unit in Standby O Unit in operationAssumptions1. The system consist of 3 components/units2. Initially two units are in operable condition of full capacity3. The system is failed when the number of working component goes down below 24. Failure and repair time follow exponential distribution5. Repair is as good as new(Perfect repair). ,
,  ,
,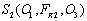 ,
, 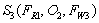 ,
,  ,
, ,
, 
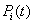 to be the probability that the system at time
to be the probability that the system at time 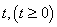 is in state
is in state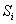 . Let
. Let  be the probability row vector at time
be the probability row vector at time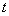 , the initial condition for this paper are
, the initial condition for this paper are 
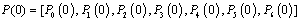
 we obtain the following differential equations:
we obtain the following differential equations: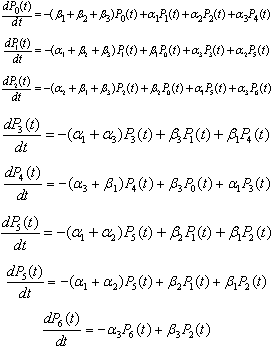
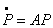 Where
Where It is difficult to evaluate the transient solutions hence following[3,4,7] we delete the rows and columns of absorbing state of matrix
It is difficult to evaluate the transient solutions hence following[3,4,7] we delete the rows and columns of absorbing state of matrix 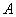 and take the transpose to produce a new matrix, say
and take the transpose to produce a new matrix, say . The expected time to reach an absorbing state is obtained from
. The expected time to reach an absorbing state is obtained from 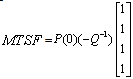
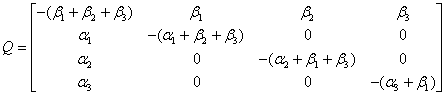 The steady state mean time to system failure is:
The steady state mean time to system failure is: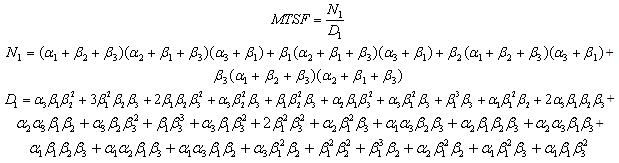
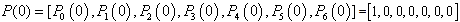 The differential equations can be expressed as
The differential equations can be expressed as The steady-state availability is given by
The steady-state availability is given by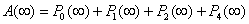
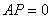
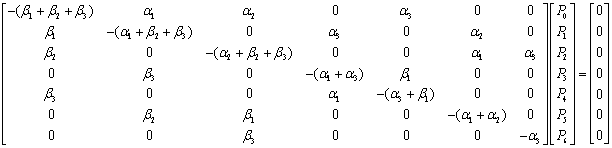 Using the following normalizing condition
Using the following normalizing condition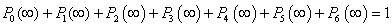
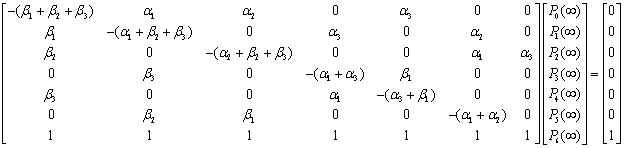 We solve for the system of equations in the matrix above to obtain the steady-state probabilities
We solve for the system of equations in the matrix above to obtain the steady-state probabilities 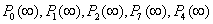 The steady-state availability is given by
The steady-state availability is given by 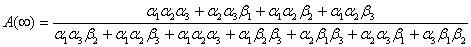
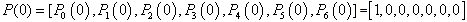 The differential equations can be expressed as
The differential equations can be expressed as 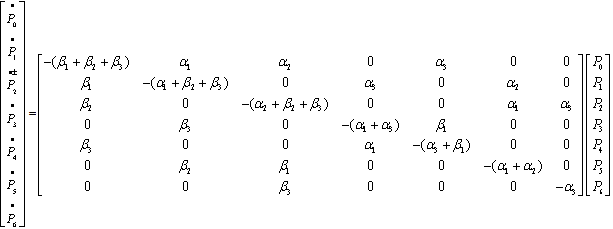 In the steady state, the derivatives of the state probabilities become zero and this will enable us to compute steady state busy :
In the steady state, the derivatives of the state probabilities become zero and this will enable us to compute steady state busy :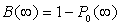
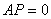 , which in matrix form
, which in matrix form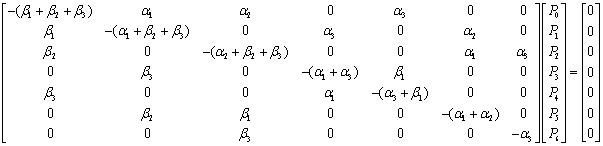 We solve for
We solve for 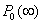 Using the following normalizing condition
Using the following normalizing condition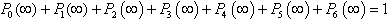
 The steady state busy period
The steady state busy period  is therefore
is therefore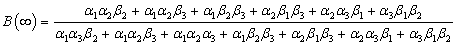

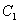 : is the cost per unit time which the system is under repair
: is the cost per unit time which the system is under repair while other parameters are kept fixed as
while other parameters are kept fixed as 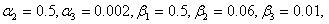
 ,From Fig. 2 it is clear that MTSF increases with increase in the value of which reflects the effect of perfect repair on MTSF. From Fig. 3 the system availability increases with increase in the value of
,From Fig. 2 it is clear that MTSF increases with increase in the value of which reflects the effect of perfect repair on MTSF. From Fig. 3 the system availability increases with increase in the value of  . Thus, the more the repair is perfect, the more the system is available for operation. In Fig. 4 it can be observed that with increase in the value of
. Thus, the more the repair is perfect, the more the system is available for operation. In Fig. 4 it can be observed that with increase in the value of 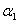 the profit also increase. Thus, the more the system is in perfect condition the more it is effective. Same argument can also be observe in table 1 where increase in the value of
the profit also increase. Thus, the more the system is in perfect condition the more it is effective. Same argument can also be observe in table 1 where increase in the value of 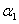 lead to the increase in profit function.
lead to the increase in profit function.

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML