Nabendu Sen
Department of Mathematics, Assam University , Pin-788011, Silchar, India
Correspondence to: Nabendu Sen , Department of Mathematics, Assam University , Pin-788011, Silchar, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Application of Goal Programming in industry is an important tool to planners. A Goal programming model regarding tea production in Barak Valley[7] and its extension developed here have been presented. The proposed models yield optimal solutions. It is very easy to understand which can serve managers by providing optimal solution to different goals involving production, profit, demand etc. With the help of numerical example, the proposed models have been validated. Finally analyses of the results obtained have been carried out. It is found that total production goal can be achieved along with other goals in both the models. The two models are compared and the former is found to be more efficient than latter.
Keywords:
Goal Programming, Management, Production, Optimization
1. Introduction
Planning and production are known to be responsible for the development of an industry. Barak valley of Assam (India) is full of green tea gardens and some of them are producing made tea from green leafs. The management of tea industries of similar nature is having different objectives to attain them within specified period of time. In this section some literatures on Goal programming and its application have been presented before the analysis of the models.Goal programming and its applications in diverse field have been studied by different authors. Cobb and Warner[1],Trivedi[2] used Goal programming model to allocate resources in management related problems of quality service. Nja and Udafia[3] applied Goal programming to flour producing companies. Vivekanandan etl[4] developed Goal Programming model for the optimization of cropping pattern for a particular region. Shim and Siegel[5] developed Goal programming model with sensitivity analysis to determine the decision variables and goal deviations. Pati etl[6] developed a mixed integer goal programming model for paper recycling system. The goals considered in the model have economical, social as well as quality implications on the paper recycling industry. Further we can find some of the important literature on goal programming in[8-15]. Recently Sinha and Sen[7] developed Goal programming model regarding tea production of different grades in tea industries of Barak Valley of Assam(India). For best author’s knowledge, no empirical study has been carried out so far to measure the effect of reduced cost, dual price on these developed models. With these above motivations, an effort has been made to study the effect of reduced cost, dual price and change of priorities of goals on these models.
2. Mathematical Models
In[7], a Goal Programming model has been formulated keeping in view environmental conditions of this valley and management point of view. The authors have focused mainly on the production of different grades (according to size) of tea as the main goal and the others goals are set on profit, factory expenditure (production expenditure),demand and over use of different machines assigned for sorting and packing. These goals are given priorities according to their importance. In the extended model of[7], goals on production of different grades of teas are kept in same priority level. Both the models have been given in appendix A and B respectively.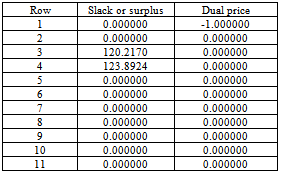
3. Numerical Illustration
Now we illustrate these two models with numerical values given in appendix C. LINGO software has been used to solve these models.The solution of model in appendix A is obtained in 10 iterations which is given below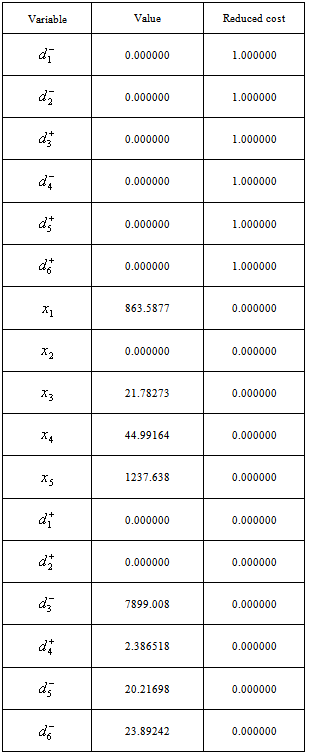 The solution of model in appendix B is obtained in 17 iterations which is given below
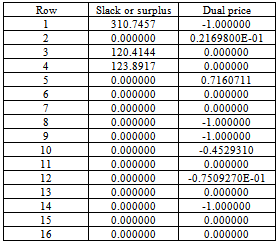
The solution of model in appendix B is obtained in 17 iterations which is given below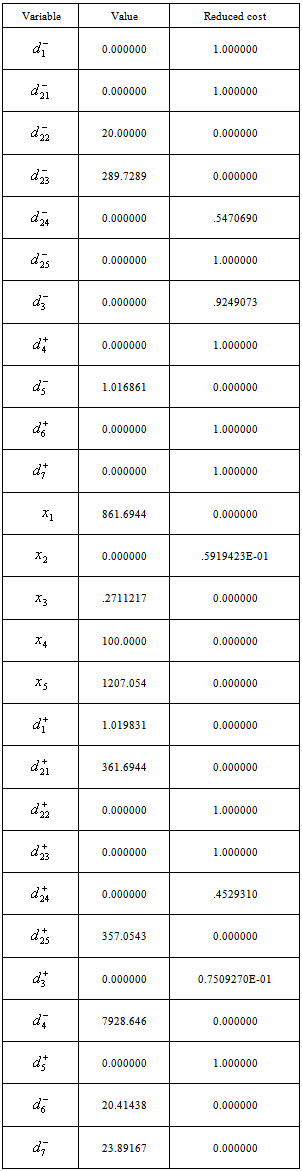
4. Analysis of the Results
4.1. Analysis of Results of First Model
The production goal and profit goal are fully achieved. The deviational variable d 3 - = 7899.008 means that there is a savings of Rs 7899.008 and the deviational variable d 4 + = 2.386518 shows that there is more demand of 2.386518 kg which can be met with the present production. Our aim is to minimize over use of both the machines but the solution reveals that the machines need not be over used as it is clear from the system constraints on time that the stipulated time is not fully used.The values of the decision variables indicate that out of five grades, the production of four grades provide optimal solution.The reduced cost of a variable is the quantity by which the solution deteriorates if we bring that variable in the present solution with same coefficient. So, reduced cost of x2 is 0 does not make any change in the solution if we introduce it also.Dual price mean the quantity by which objective value will improve if we increase the right hand side of constraints by unit quantity. In this solution it is found that there is no dual price associated with any of the constraints.It has also been observed that on changing priorities between (1stand2nd), (1st and 3rd), (1stand 4th), (2nd and 3rd), (2ndand 4th) the present form of this model gives better solution.
4.2. Analysis of Results of Second Model
The second model is the extension of first model. The additional goals are set on the production of individual grades of tea. Here total production goal is achieved and moreover the deviational variable d 1 + = 1.019831 means that there is a scope of producing 1.019831kg more. The goals on individual production of various grades are not fully achieved in case of 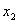 and
and 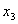 which are kept in second priority and also the deviational variables
which are kept in second priority and also the deviational variables 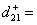 361.6944 and d 25 + =357.0543 show towards more production of the grade
361.6944 and d 25 + =357.0543 show towards more production of the grade 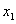 and
and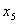 .The values of decision variables as found, give optimal solution to this extended model. The profit goal is achieved at the expense of individual production goal. One can easily understand about the reduced cost and dual price also. Change of priorities among the goals does not alter the present solution.
.The values of decision variables as found, give optimal solution to this extended model. The profit goal is achieved at the expense of individual production goal. One can easily understand about the reduced cost and dual price also. Change of priorities among the goals does not alter the present solution.
5. Concluding Remarks
This paper has mainly focused on the use of linear goal programming to make decision makers of tea industry to achieve for production management situation. The models presented in this study involve 10 constraints and 5 decision variables other than deviational variables in first model and 15 constraints in second model with same number of decision variables. On comparison of these two models in this case it is found that first model gives us better objective value than the other. It is to be mention here that the second model is developed by considering the situation where tea industry may have wish to produce different grades of tea due to some compulsion. The present study not only gives satisfying solution but also provides other relevant information. Management can find in advance what will happen if outcome deviates from objectives. The study of range of coefficients and range of right hand side of constraints will help to understand the scenarios in better way. The present study can further be extended by introducing new constraints, variables and applying fuzzy logic to these models will be of immense help for futher study.
ACKNOWLEDGEMENTS
Author express sincere thanks to the concern tea industry for providing necessary information. Author also express thanks to Prof.N.K Diwedi ,Banaras Hindu University for encouragement to carry out research in Goal Programming. Definitions of symbols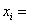 Quantity of tea of i-th grade.Total budget for expenditure for a month.
Quantity of tea of i-th grade.Total budget for expenditure for a month.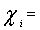 Budget per unit for i-th grade of tea.
Budget per unit for i-th grade of tea.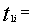 Time required in machine 1 per unit of i-th grade.
Time required in machine 1 per unit of i-th grade.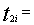 Time required in machine 2 per unit of i-th grade.
Time required in machine 2 per unit of i-th grade.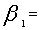 Total allotted time in machine 1 for a month.
Total allotted time in machine 1 for a month.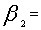 Total allotted time in machine 2 for a month
Total allotted time in machine 2 for a month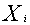 =25
=25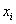 .
.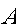 =Total allotted space for storage of packed tea.
=Total allotted space for storage of packed tea.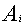 =space required by
=space required by 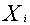 .
.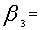 Desired amount of production goal for a month
Desired amount of production goal for a month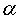 =Desired amount of profit for a month.
=Desired amount of profit for a month.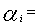 The profit per unit of i-th grade
The profit per unit of i-th grade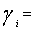 The amount to be spent for production per quantity of i-th grade of tea in factory.Desired amount to be spent for production of tea in factory in a month.
The amount to be spent for production per quantity of i-th grade of tea in factory.Desired amount to be spent for production of tea in factory in a month.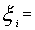
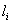 % of demand of total quantity of
% of demand of total quantity of 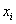 .
.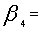 Total expected demand of all grades of tea to be met in a month.
Total expected demand of all grades of tea to be met in a month.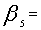 Allowable time for over use of machine 1 in a month.
Allowable time for over use of machine 1 in a month.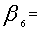 Allowable time for over use of machine 2 in a month.
Allowable time for over use of machine 2 in a month.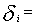 Production target of i-th grade of tea in a month.
Production target of i-th grade of tea in a month.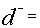 under-achievement of goals.
under-achievement of goals.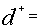 over-achievement of goals.I=The grade of tea depending upon the size=1, 2,3,4,5.
over-achievement of goals.I=The grade of tea depending upon the size=1, 2,3,4,5.
Appendix A
Achievement Function:Minimize Z= 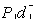 +
+ 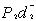 +
+ 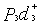 +
+ 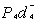 +
+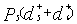 .Subject to,System Constraints:Total budget constraint
.Subject to,System Constraints:Total budget constraint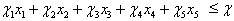 | (A.1) |
Allowable time constraints on two machines are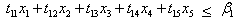 | (A.2) |
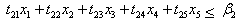 | (A.3) |
Inventory space constraint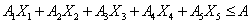 | (A.4) |
Goal Constraints:Priority P1Total Production Goal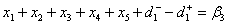 | (A.5) |
Priority P2Profit Goal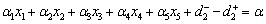 | (A.6) |
Priority P3Production Expenditure Goal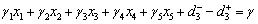 | (A.7) |
Priority P4Goal on Total Demand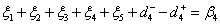 | (A.8) |
Priority P5Goal on Over Use of Machines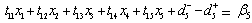 | (A.9) |
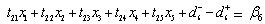 | (A.10) |
Appendix B
Achievement Function: 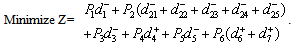 Subject to,System Constraints:Total budget constraint
Subject to,System Constraints:Total budget constraint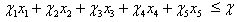 | (B.1) |
Allowable time constraints on two machines are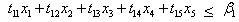 | (B.2) |
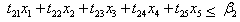 | (B.3) |
Inventory space constraint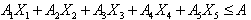 | (B.4) |
Goal Constraints:Priority P1Total Production Goal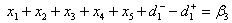 | (B.5) |
Priority P2Goal on Production of Different Grades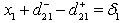 | (B.6) |
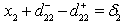 | (B.7) |
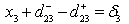 | (B.8) |
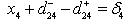 | (B.9) |
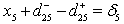 | (B.10) |
Priority P3Profit Goal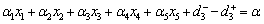 | (B.11) |
Priority P4Production Expenditure Goal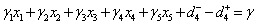 | (B.12) |
Priority P5Goal on Total Demand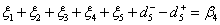 | (B.13) |
Priority P6Goal on Over Use of Machines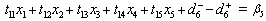 | (B.14) |
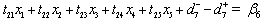 | (B.15) |
Where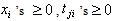 and
and 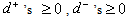 with the condition
with the condition 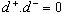
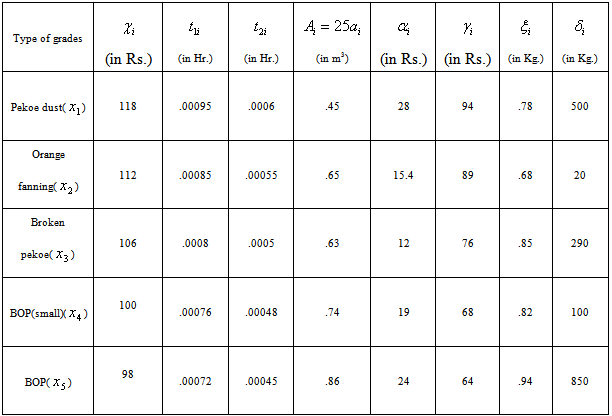
Appendix C
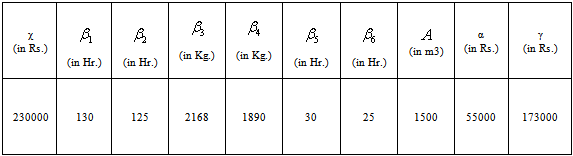
Table C.1.
 |
| |
|
Table C.2.
 |
| |
|
References
| [1] | P. Cobb , D.M. Warner, Task substitution among skill classes of nursing personnel, Nursing Res.22(1973)130-137. |
| [2] | V.M. Trivedi, A mixed integer goal programming model for nursing service budgeting, Operat.Res.29(1981)1019-1034. |
| [3] | M.E.Nja, G.A. Udofia, Formulation of the mixed integer goal programming model for flour producing companies, Asian Journal of Mathematics and Statistics.2(3) (2009)55-64. |
| [4] | N.Vivekanandan, K.Viswanathan, Sanjeev Gupta, Optimization of cropping pattern using goal programming approach,OPSEARCH.46(3)(2009)259-274. |
| [5] | J.K. Shim, J.Siegel, Sensitivity analysis of goal programming with preemption, Int.J.Syst.Sci.11(1980)393-401. |
| [6] | R.K Pati,P Vrat,P Kumar, A goal programming model for paper recycling system, Omega 36 (2008) 405 – 417. |
| [7] | B.Sinha, N.Sen, Goal Programming approach to tea Industry of Barak Valley of Assam, Applied Mathematical Sciences5 (29)(2011)1409-1419. |
| [8] | N.Mansour,A Rebai,B.Aouni, Prortfolio selection through imprecise goal programming model: Integration of the maneger’s preferences, Journal of Industrial Engineering International 3(5)(2007)1-8. |
| [9] | M Mezghani,T Loukil, A goal programming model for aggregate production planning problem,Int J of operational research 4(1)(2009)23-34. |
| [10] | H El-Shishiny, A goal programming model for planning the development of newly reclaimed lands, Agricultural System 26(1988) 245-261. |
| [11] | D K Sharma,D Gosh, D M Mattison, An application of goal programming with penalty functions to transshipment problems, Int J of Logistics:Research and applications 6(3)(2003)125-136. |
| [12] | A Gupta,G W Evan,A goal programming model for the operation of closed-loop supply chains,Engineering optimization 41(8)(2009)713-735. |
| [13] | F Jolai,M Aghdaghi,A goal programming model for single vehicle routing problem with multiple routes, journal of industrial and system engineering 2(2)154-163. |
| [14] | N K Kwak, C Lee,A linear goal programming model for human resource allocation in health-care organization, Journal of Medical system 21(3)(1997) 129-140. |
| [15] | J.A Alade ,D K Sharma, J K Sharma, A Multi-objective model for planning the exports of developing countries,African Economics and Business Review 1(2)(1998)23-41. |


 The solution of model in appendix B is obtained in 17 iterations which is given below
The solution of model in appendix B is obtained in 17 iterations which is given below

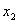 and
and 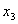 which are kept in second priority and also the deviational variables
which are kept in second priority and also the deviational variables 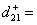 361.6944 and d 25 + =357.0543 show towards more production of the grade
361.6944 and d 25 + =357.0543 show towards more production of the grade 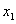 and
and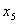 .The values of decision variables as found, give optimal solution to this extended model. The profit goal is achieved at the expense of individual production goal. One can easily understand about the reduced cost and dual price also. Change of priorities among the goals does not alter the present solution.
.The values of decision variables as found, give optimal solution to this extended model. The profit goal is achieved at the expense of individual production goal. One can easily understand about the reduced cost and dual price also. Change of priorities among the goals does not alter the present solution.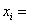 Quantity of tea of i-th grade.Total budget for expenditure for a month.
Quantity of tea of i-th grade.Total budget for expenditure for a month.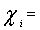 Budget per unit for i-th grade of tea.
Budget per unit for i-th grade of tea.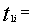 Time required in machine 1 per unit of i-th grade.
Time required in machine 1 per unit of i-th grade.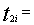 Time required in machine 2 per unit of i-th grade.
Time required in machine 2 per unit of i-th grade.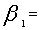 Total allotted time in machine 1 for a month.
Total allotted time in machine 1 for a month.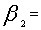 Total allotted time in machine 2 for a month
Total allotted time in machine 2 for a month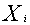 =25
=25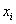 .
.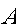 =Total allotted space for storage of packed tea.
=Total allotted space for storage of packed tea.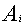 =space required by
=space required by 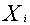 .
.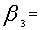 Desired amount of production goal for a month
Desired amount of production goal for a month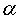 =Desired amount of profit for a month.
=Desired amount of profit for a month.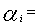 The profit per unit of i-th grade
The profit per unit of i-th grade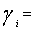 The amount to be spent for production per quantity of i-th grade of tea in factory.Desired amount to be spent for production of tea in factory in a month.
The amount to be spent for production per quantity of i-th grade of tea in factory.Desired amount to be spent for production of tea in factory in a month.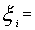
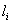 % of demand of total quantity of
% of demand of total quantity of 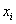 .
.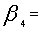 Total expected demand of all grades of tea to be met in a month.
Total expected demand of all grades of tea to be met in a month.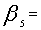 Allowable time for over use of machine 1 in a month.
Allowable time for over use of machine 1 in a month.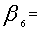 Allowable time for over use of machine 2 in a month.
Allowable time for over use of machine 2 in a month.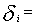 Production target of i-th grade of tea in a month.
Production target of i-th grade of tea in a month.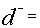 under-achievement of goals.
under-achievement of goals.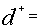 over-achievement of goals.I=The grade of tea depending upon the size=1, 2,3,4,5.
over-achievement of goals.I=The grade of tea depending upon the size=1, 2,3,4,5.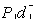 +
+ 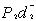 +
+ 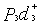 +
+ 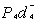 +
+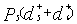 .Subject to,System Constraints:Total budget constraint
.Subject to,System Constraints:Total budget constraint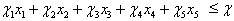
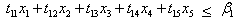
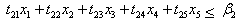
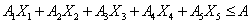
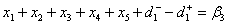
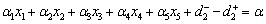
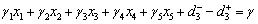
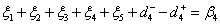
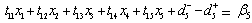
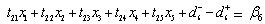
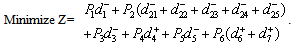 Subject to,System Constraints:Total budget constraint
Subject to,System Constraints:Total budget constraint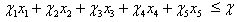
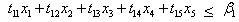
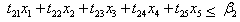
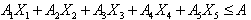
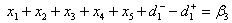
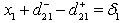
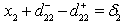
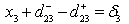
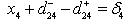
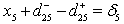
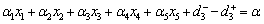
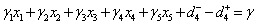
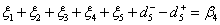
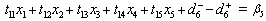
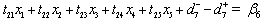
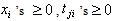 and
and 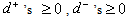 with the condition
with the condition 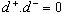
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
