1. Introduction

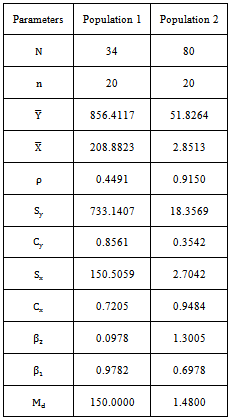
The sampling theory describes a wide variety of techniques for using auxiliary information to obtain more efficient estimators like Ratio, Product and Regression estimators for the estimation of the mean of the study variable Y. Ratio estimators, improves the precision of estimate of the population mean of a study variable by using prior information on auxiliary variable X which is positively correlated with the study variable Y. Over the years the ratio method of estimation has been extensively used because of its intuitive appeal and the computational simplicity. When the population parameters of the auxiliary variable X such as Population Mean, Co-efficient of Variation, Co-efficient of Kurtosis, Co-efficient of Skewness, Median are known, a number of modified estimators such as modified ratio estimators, modified product estimators and modified linear regression estimators are proposed in the literature. Before discussing further about the modified ratio estimators and the proposed modified ratio estimators the notations to be used in this paper are described below:

• N - Population size

• n -Sample size

• f = n/N, Sampling fraction

• Y - Study variable

• X - Auxiliary variable

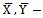• Population means

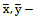• Sample means

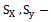• Population standard deviations

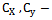• Co-efficient of variations

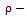• Co-efficient of correlation

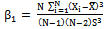• , Co-efficient of skewness of the auxiliary variable

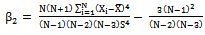•, Co-efficient of kurtosis of the auxiliary variable

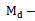• Median of the auxiliary variable

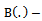• Bias of the estimator

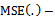• Mean squared error of the estimator

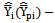• Existing (proposed) modified ratio estimator of

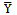The Ratio estimator for estimating the population mean 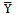of the study variable Y is defined as

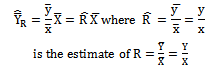(1)

The lists of modified ratio estimators together with their biases, mean squared errors and constants available in the literature are classified into two classes namely Class 1, Class 2 and are given respectively in Table 1 and Table 2 in the Appendix.

It is to be noted that “the existing modified ratio estimators” means the list of modified ratio estimators to be considered in this paper unless otherwise stated. It does not mean to the entire list of modified ratio estimators available in the literature. For a more detailed discussion on the ratio estimator and its modifications one may refer to Cochran[1], Kadilar and Cingi[2, 3], Koyuncu and Kadilar[4], Murthy[5], Prasad[6], Rao[7], Singh[9], Singh and Tailor[10,12], Singh et.al[11], Sisodia and Dwivedi[13], Subramani and Kumarapandiyan[14,15], Upadhyaya and Singh[16], Yan and Tian[17] and the references cited there in.

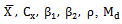The modified ratio estimators given in Table 1 and Table 2 are biased but have minimum mean squared errors compared to the classical ratio estimator. The list of estimators given in Table 1 and Table 2 uses the known values of the parameters like and their linear combinations. Recently Yan and Tian[17] have used Coefficient of Skewness for the estimation of population meanHowever, it seems, no attempt is made to use the linear combination of known values of the Median and Co-efficient of Skewness of the auxiliary variable to improve the ratio estimator. The points discussed above have motivated us to introduce two modified ratio estimators using the linear combination of the known values of Median and Co-efficient of Skewness of the auxiliary variable. When the population median and coefficient of skewness are unknown the proposed estimators can be modified using their respective estimates i.e sample median, and sample coefficient of skewness obtained from the sample. The proposed estimators can be applicable in the following practical situation.

1. A national park is partitioned into N units.

• Y = the number of animals in the i^th unit

• X = the size of the i^th unit

2. A certain city has N bookstores.

• Y = the sales of a given book title at the i^th bookstore

• X = the size of the i^th bookstore

3. A forest that has N trees.

• Y = the volume of the tree

• X = the diameter of the tree

2. Proposed Modified Ratio Estimators

In this section, we have suggested two modified ratio estimators using the linear combination of Median and Co-efficient of Skewness of the auxiliary variable. The proposed modified ratio estimators for estimating the population mean together with the first degree of approximation, the biases and mean squared errors and the constants are given below: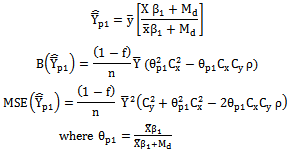

(2)

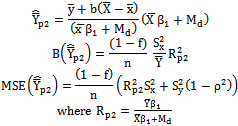(3)

3. Efficiency Comparison

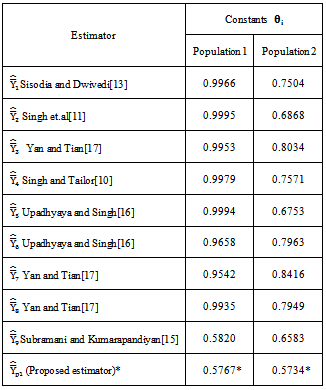
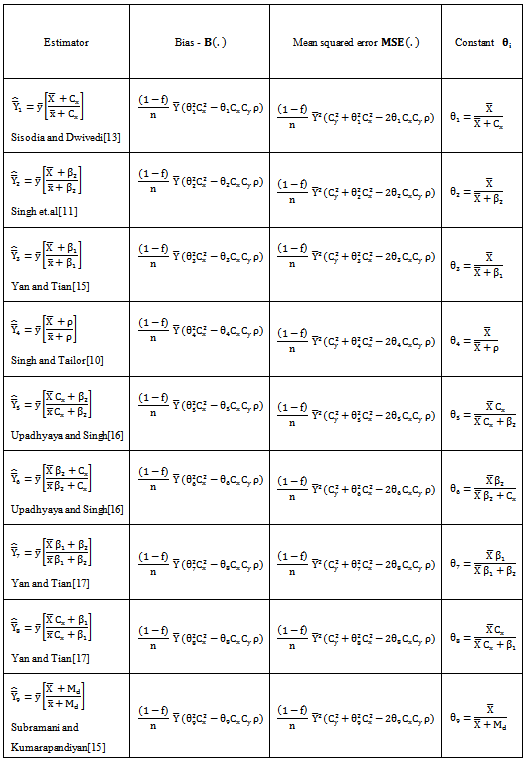
For want of space; for the sake of convenience to the readers and for the ease of comparisons, the modified ratio estimators given in Table 1, Table 2 are represented into two classes as given below. Further it is to be noted that the proposed estimator 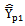is compared with the modified ratio estimators listed in Class 1 whereas the proposed estimator 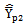is compared with the modified ratio estimators listed in Class 2.

Class 1:The biases, the mean squared errors and the constants of the modified ratio type estimators 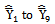listed in the Table 1 are represented in a single class (say, Class 1), which will be very much useful for comparing with that of proposed modified ratio estimators and are given below:

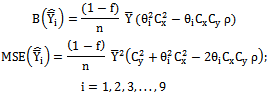(4)

where

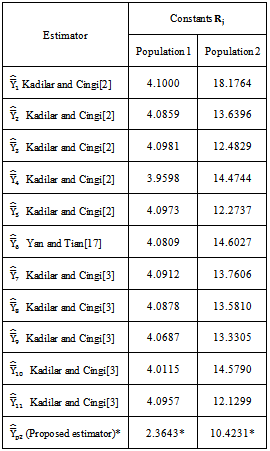
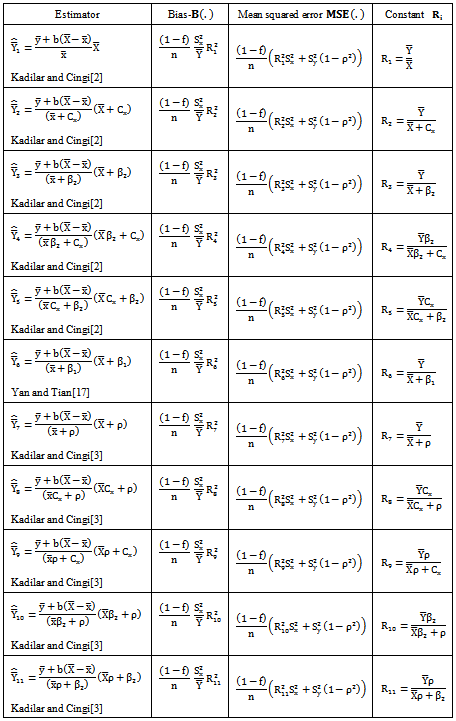
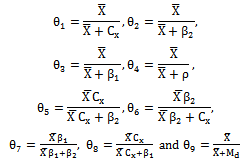Class 2:The biases, the mean squared errors and the constants of the 11 modified ratio estimators 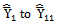listed in the Table 2 are represented in a single class (say, Class 2), which will be very much useful for comparing with that of proposed modified ratio estimators and are given below:

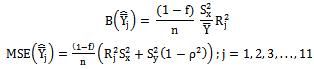(5)

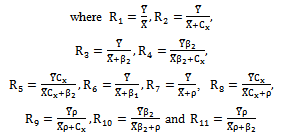As derived earlier in section 2, the biases, the mean squared errors and the constants of two proposed modified ratio estimators are given below:

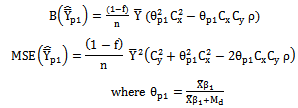(6)

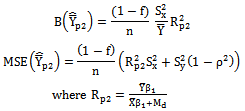(7)

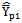From the expressions given in (4) and (6) we have derived the conditions for which the proposed estimator is more efficient than the existing modified ratio estimators given in Class 1, 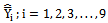and are given below.

From the expressions given in (5) and (7) we have derived the conditions for which the proposed estimator 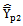is more efficient than the existing modified ratio estimators given in Class 2, 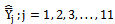and are given below:

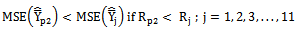(9)

4. Numerical Study

Table 3. Parameters and Constants of the Populations

Table 4. The constants of the (Class 1) existing and proposed modified ratio estimators

The performances of the proposed modified ratio estimators are assessed with that of existing modified ratio estimators listed in Table 1 and Table 2 for certain natural populations. In this connection, we have considered two natural populations for the assessment of the performances of the proposed modified ratio estimators with that of existing modified ratio estimators. The population 1 is taken from Singh and Chaudhary[8] given in page 177 and population 2 is taken from Murthy[5] given in page 228. The population parameters and the constants computed from the above populations are given below:

The constants of the existing and proposed modified ratio estimators for the above populations are given in the Table 4 and Table 5:

Table 5. The constants of the (Class 2) existing and proposed modified ratio estimators

The biases of the existing and proposed modified ratio estimators for the above populations are given in the Table 6 and Table 7:

Table 6. The biases of the (Class 1) existing and proposed modified ratio estimators

Table 7. The biases of the (Class 2) existing and proposed modified ratio estimators

The mean squared errors of the existing and proposed modified ratio estimators for the above populations are given in the Table 8 and Table 9:

Table 8. The mean squared errors of the (Class 1) existing and proposed modified ratio estimators

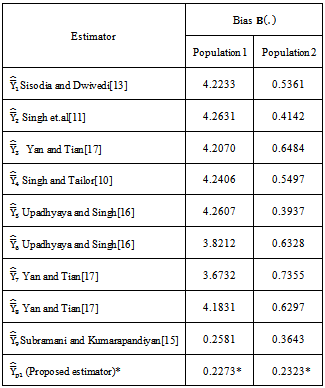
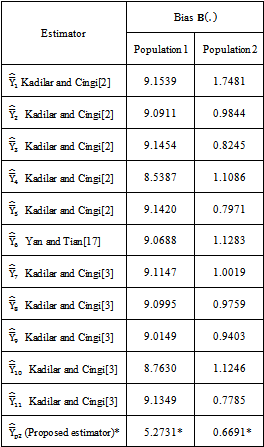
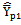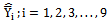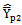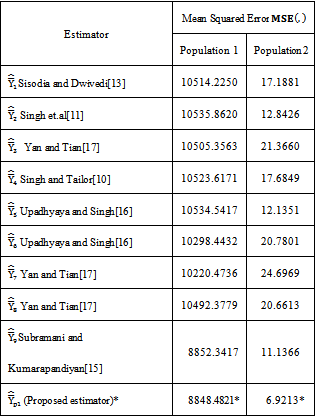
From the values of Table 6 and Table 7, it is observed that the bias of the proposed modified ratio estimator is less than the biases of the existing modified ratio estimators given in Class 1 and the bias of the proposed modified ratio estimator is less than the biases of the existing modified ratio estimators 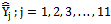given in Class 2. Similarly from the values of Table 8 and Table 9, it is observed that the mean squared error of the proposed modified ratio estimator 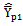is less than the mean squared errors of the existing modified ratio estimators 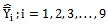given in Class 1 and the mean squared error of the proposed modified ratio estimator 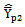is less than the mean squared errors of the existing modified ratio estimators 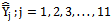given in Class 2.

Table 9. The mean squared errors of the (Class 2) existing and proposed modified ratio estimators

5. Conclusions

In this paper we have proposed two modified ratio estimators using linear combination of Median and Co-efficient of Skewness of the auxiliary variable. The biases and mean squared errors of the proposed estimators are obtained and compared with that of existing modified ratio estimators. Further we have derived the conditions for which the proposed estimators are more efficient than the existing modified ratio estimators. We have also assessed the performances of the proposed estimators for some known populations and observed that the biases and mean squared errors of the proposed estimators are less than the biases and mean squared errors of the existing modified ratio estimators. Hence we strongly recommend the proposed modified estimators over the existing modified ratio estimators for the use of practical applications.

ACKNOWLEDGEMENTS

The authors are thankful to the referees for their constructive comments. The second author wishes to thank the Vice Chancellor, Pondicherry University and other University authorities for the financial assistance to carry out this research work through the University Fellowship.

APPENDIX

Table 1. Existing modified ratio estimators (Class 1) with their biases, mean squared errors and their constants

Table 2. Existing modified ratio estimators (Class 2) with their biases, mean squared errors and their constants