-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2012; 2(4): 89-94
doi: 10.5923/j.ajms.20120204.04
A Sixth Order Implicit Hybrid Backward Differentiation Formulae (HBDF) for Block Solution of Ordinary Differential Equations
Muhammad R , Yahaya. Y. A
Department of Mathematics/Statistics, Federal University of Technology Minna, Niger State, +234, Nigeria
Correspondence to: Muhammad R , Department of Mathematics/Statistics, Federal University of Technology Minna, Niger State, +234, Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The Hybrid Backward Differentiation Formula (HBDF) for case K=5 was reformulated into continuous form using the idea of multistep collocation. Multistep Collocation is a continuous finite difference (CFD) approximation method by the idea of interpolation and collocation. The hybrid 5-step Backward Differentiation Formula (BDF) and additional methods of order 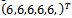 were obtained from the same continuous scheme and assembled into a block matrix equation which was applied to provide the solutions of IVPs over non-overlapping intervals.The continous form was immediately employed as block methods for direct solution of Ordinary Differential Equation
were obtained from the same continuous scheme and assembled into a block matrix equation which was applied to provide the solutions of IVPs over non-overlapping intervals.The continous form was immediately employed as block methods for direct solution of Ordinary Differential Equation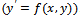 . Some benefits of this study are, the proposed block methods will be self starting and does not call for special predictor to estimate
. Some benefits of this study are, the proposed block methods will be self starting and does not call for special predictor to estimate  in the integrators and all the discrete methods obtained will be evaluated from a single continuous formula and its derivatives at various grids and off grid points. These study results help to speed up computation, also the requirement of a starting value and the overlap of solution model which are normally associated with conventional Linear Multistep Methods were eliminated by this approach. In conclusion, a convergence analysis of the derived hybrid schemes to establish their effectiveness and reliability was presented. Numerical example carried out on stiff problem further substantiates their performance.
in the integrators and all the discrete methods obtained will be evaluated from a single continuous formula and its derivatives at various grids and off grid points. These study results help to speed up computation, also the requirement of a starting value and the overlap of solution model which are normally associated with conventional Linear Multistep Methods were eliminated by this approach. In conclusion, a convergence analysis of the derived hybrid schemes to establish their effectiveness and reliability was presented. Numerical example carried out on stiff problem further substantiates their performance.
Keywords: Backward Differentiation Formula (BDF), Block Methods, Hybrid, Implicit, Multistep Collocation, Stiff
Article Outline
1. Introduction
- Most real life problems that arise in various fields of study be it engineering or science are modelled as mathematical models before they are solved. These models often lead to differential equations.
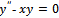 | (1) |
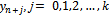 from which it will be possible to compute sequentially the sequence
from which it will be possible to compute sequentially the sequence 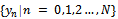 . Naturally this difference equation will also involve the function
. Naturally this difference equation will also involve the function 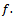 The integer k is called the step number of the method. For
The integer k is called the step number of the method. For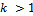 , it’s called a 1- step method and for value of
, it’s called a 1- step method and for value of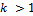 it’s called a multistep or k -step method.If a computational method for determining the sequence
it’s called a multistep or k -step method.If a computational method for determining the sequence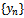 takes the form of a linear relationship between
takes the form of a linear relationship between 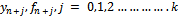 we call it a Linear Multistep Method of step number k or a Linear k-step method. These methods can be written in the general form
we call it a Linear Multistep Method of step number k or a Linear k-step method. These methods can be written in the general form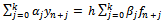 | (2) |
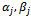 are constants and we assume
are constants and we assume 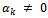 and that not both
and that not both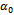 and
and 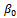 are zero. Without loss of generality we let ak=1. Explicit methods are characterized by
are zero. Without loss of generality we let ak=1. Explicit methods are characterized by 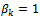 and implicit methods by
and implicit methods by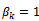 . Explicit linear multistep methods are known as Adams-Bashforth methods, while implicit linear multistep methods are called Adams-moulton methods. These methods are generally called the Adams family.Other famous classes of multistep methods aside the Adams family includes the predictor –corrector method and the Backward Differentiation Formula.The Backward differentiation formula are implicit linear k-step method with regions of absolute stability large enough to make them relevant to the problem of stiffness.Backward differentiation methods were introduced by Curtiss and Hirshfelder in 1952. For these methods
. Explicit linear multistep methods are known as Adams-Bashforth methods, while implicit linear multistep methods are called Adams-moulton methods. These methods are generally called the Adams family.Other famous classes of multistep methods aside the Adams family includes the predictor –corrector method and the Backward Differentiation Formula.The Backward differentiation formula are implicit linear k-step method with regions of absolute stability large enough to make them relevant to the problem of stiffness.Backward differentiation methods were introduced by Curtiss and Hirshfelder in 1952. For these methods 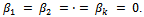 These methods play a special role in the solution of stiff problems, despite not being A-stable for methods of order 3 or above. The most widely used adaptive codes for solving stiff differential equations are based on backward differentiation methods.We consider the Initial Value Problem of the form
These methods play a special role in the solution of stiff problems, despite not being A-stable for methods of order 3 or above. The most widely used adaptive codes for solving stiff differential equations are based on backward differentiation methods.We consider the Initial Value Problem of the form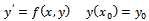 | (3) |
 Many methods for solving (1) exists, one particular method is the Linear Multistep Method. Linear Multistep Methods require less evaluation of the derivative function f than one step methods in the range of integral
Many methods for solving (1) exists, one particular method is the Linear Multistep Method. Linear Multistep Methods require less evaluation of the derivative function f than one step methods in the range of integral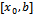 . For this reasons they have been very popular and important for solving (3) numerically. But these methods have certain limitations such as the overlap of solution models and the requirement of a starting value. Other limitations include they yield the discrete solution values
. For this reasons they have been very popular and important for solving (3) numerically. But these methods have certain limitations such as the overlap of solution models and the requirement of a starting value. Other limitations include they yield the discrete solution values 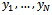 hence uneconomical for producing dense output. A continuous formulation is desirable in this respect. The collocation method is probably the most important numerical procedure for the construction of continuous methods.In this research paper, we derived the Block Hybrid Backward Differentiation Formulae (BHBDF) for
hence uneconomical for producing dense output. A continuous formulation is desirable in this respect. The collocation method is probably the most important numerical procedure for the construction of continuous methods.In this research paper, we derived the Block Hybrid Backward Differentiation Formulae (BHBDF) for 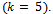 . The block methods were used to solve an Initial Value Problem directly without the need of a starting value. Their performances were compared with the analytical solution to the problem.
. The block methods were used to solve an Initial Value Problem directly without the need of a starting value. Their performances were compared with the analytical solution to the problem.1.1. The Multistep Collocation (CMM) Method
- Lambert (1973,1991) adopted the continous finite difference (CFD) approximation method by the idea of interpolation and collocation. Later, Lie and Norsett (1989), Onumanyi (1994,1999) referred to it as Multistep Collocation (MC). The method is presented below
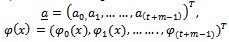 | (4) |
 are undetermined constants,
are undetermined constants, 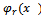 are specified basis functions, T denotes transpose of, t denotes the number of interpolation points and m denotes the number of distinct collocation points. We consider a continuous approximation (interpolant) Y(x) to y(x) in the form
are specified basis functions, T denotes transpose of, t denotes the number of interpolation points and m denotes the number of distinct collocation points. We consider a continuous approximation (interpolant) Y(x) to y(x) in the form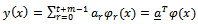 | (5) |
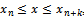 , where n = 0,k……,N – k. The quantities
, where n = 0,k……,N – k. The quantities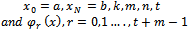 are specified values. The constant co-efficient
are specified values. The constant co-efficient 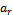 of (5) can be determined using the conditions
of (5) can be determined using the conditions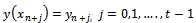 | (6) |
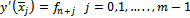 | (7) |
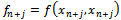 | (8) |
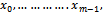 can be chosen freely from the set
can be chosen freely from the set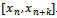 Equation (5), (6) and (7) are denoted by a single set of algebraic equations of the form
Equation (5), (6) and (7) are denoted by a single set of algebraic equations of the form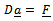 | (9) |
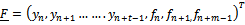 | (10) |
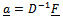 | (11) |
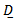 is the non-singular matrix of dimension
is the non-singular matrix of dimension 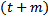
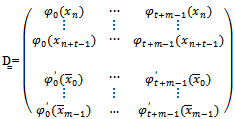 | (12) |
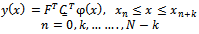 | (13) |
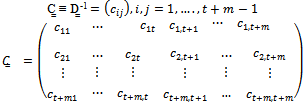 with the numerical elements denoted by
with the numerical elements denoted by 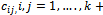
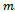 By expanding C̳Tφ(x) in (13) yields the following
By expanding C̳Tφ(x) in (13) yields the following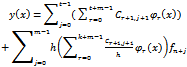 | (14) |
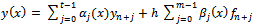 | (15) |
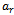 can be determined as follows:
can be determined as follows: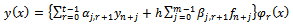
2 Problem Formulation
- For
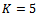 the general form of the method upon addition of one off grid point is expressed as;
the general form of the method upon addition of one off grid point is expressed as;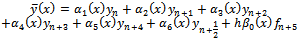 | (16) |
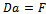 The matrix D of the proposed method is expressed as:
The matrix D of the proposed method is expressed as: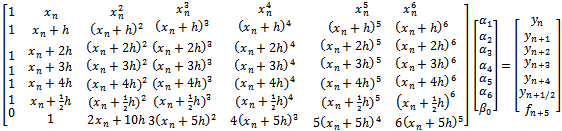 | (17) |
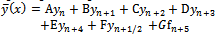 | (18) |
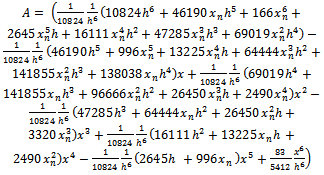



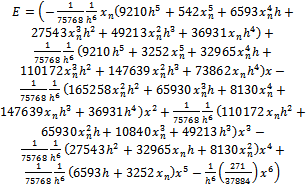
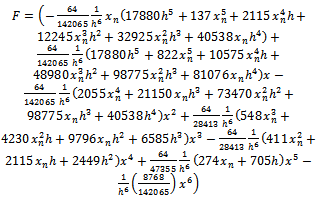
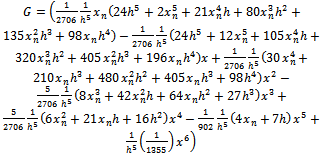 Evaluating (18) at point
Evaluating (18) at point 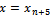 and its derivative at
and its derivative at 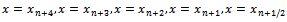 yields the following six discrete hybrid schemes which are used as block integrator:
yields the following six discrete hybrid schemes which are used as block integrator: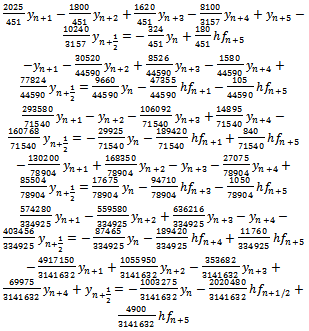 | (19) |
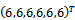 with
with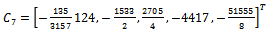 as the error constants respectively. To start the integration process with n=0, we use (19) and this produces
as the error constants respectively. To start the integration process with n=0, we use (19) and this produces 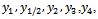 and
and 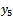 simultaneously without the need of any starting method (predictor).
simultaneously without the need of any starting method (predictor).2.1. Stability Analysis
- Following Fatunla (1992; 1994),that defined the block method to be zero-stable provided the roots
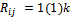 of the first characteristic polynomial
of the first characteristic polynomial 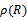 specified as
specified as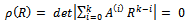 | (20) |
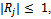 the multiplicity must not exceed 2.The block methods proposed in equation (19) for
the multiplicity must not exceed 2.The block methods proposed in equation (19) for 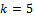 are put in the matrix equation form and for easy analysis the result was normalized to obtain
are put in the matrix equation form and for easy analysis the result was normalized to obtain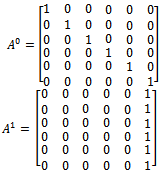 | (21) |
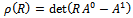 Substituting the
Substituting the 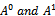 into the function above gives
into the function above gives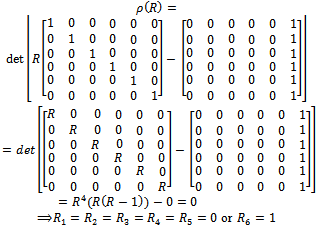 | (22) |
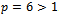 . And by Henrici(1962); the hybrid method is convergent.
. And by Henrici(1962); the hybrid method is convergent.3. Problem Solution
- To illustrate the performance of our proposed methods we will compare their performance with analytical results. Consider the initial value problem
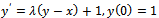 The problem is stiff in nature for negative
The problem is stiff in nature for negative 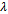 values and it has analytical solution
values and it has analytical solution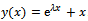 The problem is solved with
The problem is solved with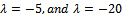 and steplength
and steplength 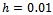 using the Block Hybrid Backward Differentiation Formulae (BHBDF) for
using the Block Hybrid Backward Differentiation Formulae (BHBDF) for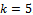 . The results were compared with analytical method and Block Hybrid Backward Differentiation Formulae (BHBDF) for
. The results were compared with analytical method and Block Hybrid Backward Differentiation Formulae (BHBDF) for 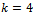
|
|
|
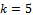 with one off grid point at
with one off grid point at 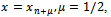 which is suitable for stiff problems. Convergence Analysis of the resulting discrete block hybrid method was done using the zero stability theory of fatunla (1992;1994) for k step block methods. Numerical Experiment for stiff initial value problem was carried out. Results obtained for the problem implemented by our present method was tabulated. The BHBDF for K= 5 is of higher accuracy and performance than BHBDF for K= 4 for both Eigen values (λ = -5 and λ = -20). The block methods produce accurate results when compared with analytical results.
which is suitable for stiff problems. Convergence Analysis of the resulting discrete block hybrid method was done using the zero stability theory of fatunla (1992;1994) for k step block methods. Numerical Experiment for stiff initial value problem was carried out. Results obtained for the problem implemented by our present method was tabulated. The BHBDF for K= 5 is of higher accuracy and performance than BHBDF for K= 4 for both Eigen values (λ = -5 and λ = -20). The block methods produce accurate results when compared with analytical results.4. Conclusions
- We have derived the hybrid form of the Backward Differentiation Formulae (BDF) for
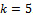 . The idea of Multistep Collocation (MC) was used to reformulate the derived hybrid formulae into continous form which were immediately employed as block methods for direct solution of
. The idea of Multistep Collocation (MC) was used to reformulate the derived hybrid formulae into continous form which were immediately employed as block methods for direct solution of 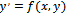 . A convergence analysis of the discrete hybrid methods to establish their effectiveness and reliability is presented. The methods were tested on stiff IVP and shown to perform satisfactorily without the requirement of any starting method. The newly constructed methods speed up computation and eliminate the overlap of solution model.
. A convergence analysis of the discrete hybrid methods to establish their effectiveness and reliability is presented. The methods were tested on stiff IVP and shown to perform satisfactorily without the requirement of any starting method. The newly constructed methods speed up computation and eliminate the overlap of solution model.ACKNOWLEDGEMENTS
- I like to express my profound gratitude to no other than my thesis supervisor, Dr Y. A Yahaya, for his guidance, constructive criticisms and intellectual inspiration from the very beginning through to the completion of this work.To all my teachers, especially Prof. K.R Adegboye, Prof N.I Akinwande, Prof Y.M Aiyesimi, Dr U.Y Abubakar, Dr L.N Ezeako and all others too numerous to mention, who have contributed in one way or the other toward the attainment of my educational pursuits, culminating in what I am today, an enlightened individual, I forever remain grateful. Same goes to all staff and students of Department of Mathematics/Statistics of Federal University of Technology, Minna.To my parents, husband, children and other members of my family, for providing an enabling environment in the home conducive enough to undertake a research studies, I say a big thank you.And lastly but not the least, I must express my high indebtedness to all whose works I have found indispensable in the course of this research. All such have been duly acknowledged.
References
| [1] | Awoyemi, D.O, “A fourth Order Continous Hybrid Multistep Method for Initial Value Problems of Second Order Differential Equations”, Spectrum Journal, Vol. 1, No.2, pp. 70-73, 1994. |
| [2] | Awoyemi, D.O, “A class of continous methods for General Second Order Initial Value Problems in Ordinary Differential Equations”, International Journal of Computer Mathematics, Vol. 72,pp. 29-37,1999. |
| [3] | Chapra,S.C. and Canale,R.P, Numerical Methods For Engineers,Third Edition, McGraw-Hill, 1998. |
| [4] | Fatunla, S.O, “New Predictor-Corrector Formulas”, Nigerian Journal of Pure And Applied Science, vol. 2, pp. 51-70. 1987. |
| [5] | Fatunla, S.O, Block methods for Second Order Initial Value Problem, International Journal of Computer Mathematics, Vol. 41,pp.55-63,1994. |
| [6] | Fatunla,S.O, Ikhile M.N.O, Otunta F.O, A class of P-Stable Linear Multistep Numerical methods. International Journal of Computer Mathematics, Vol. 72, pp. 1-13, 1999. |
| [7] | Henrici, P, “Discrete Variable methods for Ordinary Differential Equations”, John Wiley, New York,USA,1962. |
| [8] | Joshua, P.C, “A study of block hybrid Adams methods with link to 2 step R-K methods for first order Ordinary Differential Equation”, Ph.D Thesis (unpublished), University of Jos, Nigeria, 2004. |
| [9] | Khairil, I.O., Zarina, B.I., Mohammed,S., “Parallel Block Backward Differentiation Formulas for Solving Ordinary Differential Equations”, Proceedings of World Academy of Science, Engineering and Technology, Vol.30, pp 54-56 2008. |
| [10] | Lambert, J.D Computational Methods in Ordinary Differential Equations. John Wiley &Sons. New York, 1973. |
| [11] | Lambert, J.D, “Numerical methods for Ordinary Differential Systems: The Initial Value Problem”, John Wiley &Sons, New York, pp. 293, 1991. |
| [12] | Lie, I and Norsett, S.P, “Super Convergence for Multistep Collocation”, J.Math Comp.52, pp. 65-79, 1989. |
| [13] | Milne, N.E, “Numerical Integration Of Ordinary Differential Equations”. Amer math monthly 33 pp. 45-460, 1926. |
| [14] | Okunuga, S.A, Akinfenwa, A.O and Daramola, A.R, “One-point Variable Step Block methods for Solving Stiff Initial Value Problems’. Proceedings of Mathematical Association of Nigeria (M.A.N) Annual National Conference (J.S.Sadiku editor) pp. 33-39, 2008. |
| [15] | Okunuga, S.A, “A Fourth Order Composite Two Step Methods For Stiff Problems”, International Journal of Computer Mathematics,Vol 72,pp. 39-47, 1999 |
| [16] | Onumanyi,P, Oritz, E.L, and Samara, H, “Software For A Method Of Finite Approximations For the Numerical Solution of Differential Equations”, Applied Mathematical Modeling, vol5 pp. 282-286, 1981 |
| [17] | Onumanyi.P, Awoyemi,D.O, Jator S.N, Sirisena,U.W, “New Linear Multistep Methods With Continous Coefficient For First Order Initial Value Problems”, Journal of the Nigerian Mathematical Society. Vol 13, pp. 27-51, 1994. |
| [18] | Onumanyi,P, Sirisena,U.W, Jator S.N, “Continous Finite Difference Approximations For Solving Differential Equations”, International Journal of Computer Mathematics, Vol 72, pp. 15-27, 1999. |
| [19] | Sokoto, A.M, “ A class of Hybrid Adams-Moulton Methods for the solution of First Order Initial Value Problems in Ordinary Differential Equations”, M.Sc Thesis (unpublished), Nigerian Defence Academy, Kaduna. pp. 58-61, 2009. |
| [20] | Yahaya, Y.A, “Some theories and Application of Continouos Linear Multistep Methods for Ordinary Differential Equations”, Ph.D Thesis (unpublished), University of Jos, Nigeria, 2004. |
| [21] | Y.A Yahaya and Z.A Adegboye, “A New Quade’s type four step Block Hybrid Multistep method for accurate and efficient parallel solution of Ordinary Differential Equations”, Abacus, Journal of the Mathematical Association of Nigeria, vol 34, No 2B, pp. 271-278, 2007. |
| [22] | Yahaya Y.A and Umar Mohammed, “A reformulation of implicit five step backward differentiation formular in continous form for solution of first order Initial Value Problem”, Journal of General Studies (JOG), Vol. 1. No 2, pp. 134-144, 2009. |
| [23] | Yahaya Y.A, Sokoto A.M, and Shaba, M.M, “Towards an efficient Computational Treatment of Block Hybrid Adams-moulton Methods for the solution of first order Initial Value Problems in Ordinary Differential Equations”, International Journal of Numerical Mathematics (IJNM),Vol. 5, No 2, pp. 264-274, 2010. |
| [24] | Yahaya Y.A, Umar Muhammad, “Fully Implicit three point Backward Differentiation Formulae for solution of first order Initial Value Problems”, International Journal of Numerical Mathematics (IJNM), Vol.5, No 3, pp. 384-398, 2010. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML