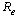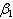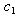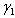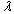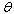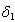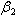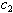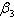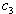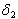Ratera Safiel 1, Estomih S. Massawe 1, Daniel Oluwole Makinde 2
1Mathematics Department, University of Dar es Salaam, P. O. Box 35062, Dar es Salaam, Tanzania
2Institute for Advance Research in Mathematical Modelling and Computations, Cape-Peninsula University of Technology, P.O.Box 1906, Bellville 7535, South Africa
Correspondence to: Estomih S. Massawe , Mathematics Department, University of Dar es Salaam, P. O. Box 35062, Dar es Salaam, Tanzania.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper examines the effect of screening and treatment on the transmission of HIV/AIDS infection in a population. A nonlinear mathematical model for the problem is proposed and analysed qualitatively using the stability theory of the differential equations. The effective reproduction number of the normalised model system (3) was obtained by using the next generation operator method. The results show that the disease free equilibrium is locally stable by using Routh Hurwitz criteria at threshold parameter less than unity and unstable at threshold parameter greater than unity. Globally, the disease free equilibrium is not stable due existence of forward bifurcation at threshold parameter equal to unity. Using Lyapunov method, endemic equilibrium is globally stable under certain conditions. However, analysis shows that, screening of unaware HIV infectives and treatment of screened HIV infectives have the effect of reducing the transmission of the disease. Numerical simulation of the model is implemented to investigate the sensitivity of certain key parameters on the voluntary screening and treatment of the screened infectives and full blown AIDS victims.
Keywords:
HIV/AIDS, Screening of HIV, HIV Treatment with ARV, Equilibrium; Stability, Reproduction Number, Sensitivity Index
1. Introduction
The acquired immunodeficiency syndrome (AIDS) emerged in 1981 and has become an alarming sexuality transmitted disease throughout the world. HIV has shown a high degree of prevalence in populations all over the world [1]. It is common to young and adults. Individuals aged 15years and above are the most susceptible group of acquiring infection[2]. This is because they are sexually active and thus capable of reproduction. Routine screening of unaware infectives have now become an integral part of programs in low and middle income countries. People can get HIV tests at a health clinic, at special HIV voluntary counselling and testing (VCT) sites (UNAIDS, 2002). Screening for HIV facilitates immune system monitoring and early management of side infections and sexually transmitted infections (STI’s) which can greatly improve long term health. It also facilitates referral to social and peer support. HIV positive test may help in changing behaviours that may help in transmitting infections. It also enables infectives to be aware and immediately take advantage of antiretroviral therapy (ART) that will help to manageinfections and delay the onset of HIV symptoms. Improvement to access to HIV testing and counselling and antiretroviral therapy could significantly reduce infection rates ([3],[4]). Estimates developed through epidemiological modelling suggest that HIV related mortality can be reduced by 20% between 2010 and 2015 if the guidelines for early treatment are broadly implemented The link between infectious diseases and screening must be understood in relation to infectives on the spread of HIV infections. From the initial models of[5, 6, 7], various refinements have been added into modelling frameworks, and specific issues have been addressed by[8, 9, 10, 11].So far few studies have been developed to analyse mathematically the impact of the screening of unaware infectives on the spread of HIV infections in a homogeneous population. However, none of these studies had considered the aspect of screening and treatment on the transmission of HIV/AIDS infections. It is well known that treatment of screened infectives may also play a major role in the transmission dynamics of the disease in a homogeneous population.[1] presented a theoretical framework for transmission of HIV/AIDS with screening of unaware infectives.[12] established and analyzed a mathematical model of the effect of screening the HIV infection in a homogeneous population with infective immigrants. However, in all the above studies, none of them incorporated the treatment of screened infectives and full blown AIDS patients. In this paper, it is therefore intended to analyze a model which will incorporate screening and treatment on the transmission of HIV/AIDS infection in a population. This is an extension of the work by[5] and the work by[12], by including the aspect of treatment of screened infectives in a homogeneous population in order to put more knowledge on the long and short term behaviour of the dynamics of the disease transmission and predict whether the disease will disappear (curbing down) or will persist. Thus we study and analyze a non linear mathematical model of the effect of screening and treatment on transmission of HIV/AIDS infection in a population. The model incorporates the assumption that all three invectives (Unaware infectives, Screened infectives and Treated infectives) move to full blown AIDS at different rates.
2. Model Formulation
A non linear mathematical model is proposed and analysed to study the effect of screening and treatment on transmission of HIV/AIDS infection in a population. The proposed model subdivides the population of interest into five sub population compartments depending on the HIV status of individuals. In modelling the dynamics, the population is divided into five subclasses: Susceptibles ‘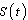 ’, Unaware infectives ‘
’, Unaware infectives ‘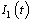 ’, Screened infectives ‘
’, Screened infectives ‘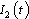 ’, Treated class ‘
’, Treated class ‘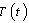 ’ and Full blown AIDS class ‘
’ and Full blown AIDS class ‘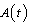 ’. The susceptibles are individuals that have not contracted the HIV infection (HIV negative); the unaware infectives are individuals that have contracted the HIV infection but are not aware of their infection; the screened infectives are individuals that have contracted the HIV infection and are known to be infected after being detected by a medical screening method, treated class (not cured but undergoing treatment) are individuals who use ARV(anti retrovirus) therapy after being screened and become screened infectives or develop full blown AIDS.In formulating the model, the following assumptions are taken into consideration:(i) The rate of transmission is direct proportional to the susceptibles population and also to the ratio between the members of infected population to the total population.(ii) Only screened infectives and full blown AIDS can be treated with ARV therapy (i.e. can move to treated class) at different rates
’. The susceptibles are individuals that have not contracted the HIV infection (HIV negative); the unaware infectives are individuals that have contracted the HIV infection but are not aware of their infection; the screened infectives are individuals that have contracted the HIV infection and are known to be infected after being detected by a medical screening method, treated class (not cured but undergoing treatment) are individuals who use ARV(anti retrovirus) therapy after being screened and become screened infectives or develop full blown AIDS.In formulating the model, the following assumptions are taken into consideration:(i) The rate of transmission is direct proportional to the susceptibles population and also to the ratio between the members of infected population to the total population.(ii) Only screened infectives and full blown AIDS can be treated with ARV therapy (i.e. can move to treated class) at different rates 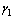 and
and 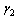 respectively.(iii) Unaware infectives, screened infectives and treated class will move to full blown AIDS at different rates
respectively.(iii) Unaware infectives, screened infectives and treated class will move to full blown AIDS at different rates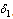 ,
, 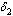 and
and 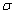 respectively where
respectively where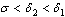 . (iv) Unaware infectives can only move to screened class and full blown AIDS and unaware infective can be screened at a rate ‘
. (iv) Unaware infectives can only move to screened class and full blown AIDS and unaware infective can be screened at a rate ‘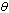 ’.(v) Unaware infectives, screened infectives and treated class can infect susceptibles class at different rates
’.(v) Unaware infectives, screened infectives and treated class can infect susceptibles class at different rates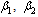 and
and 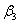 respectively where
respectively where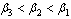 .Following mixing of susceptibles, unaware infectives, screened infectives, treated class and full blown AIDS patients, susceptibles acquire HIV infection with the force of infection
.Following mixing of susceptibles, unaware infectives, screened infectives, treated class and full blown AIDS patients, susceptibles acquire HIV infection with the force of infection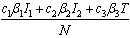 . The population considered to be homogeneously mixed and each susceptible individual has equal chance of acquiring HIV infection when comes into contact with infectious individual. The population under study comprises of persons with at least 15 years, so in this case it is assumed that there is no vertical transmission and all recruitment are natural birth without disease, population is variable and all parameters are positive. Taking into account the above considerations, we then have the following schematic flow diagram:
. The population considered to be homogeneously mixed and each susceptible individual has equal chance of acquiring HIV infection when comes into contact with infectious individual. The population under study comprises of persons with at least 15 years, so in this case it is assumed that there is no vertical transmission and all recruitment are natural birth without disease, population is variable and all parameters are positive. Taking into account the above considerations, we then have the following schematic flow diagram: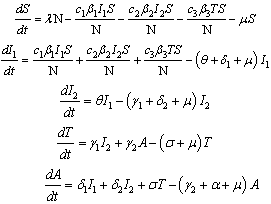 | (1) |
where 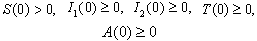 The total population at time is given by,This gives
The total population at time is given by,This gives | (2) |
We note that in the absence of the disease, the total population size N is stationary for 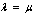 declines for
declines for 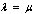 and grows exponentially for
and grows exponentially for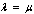 . So we shall assume that mortality rate
. So we shall assume that mortality rate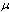 , will be a function of state variables. For convenience, we analyse our model in terms of proportions of quantities instead of actual populations. This can be done by scaling the population of each class by the total populations. We make the transformation
, will be a function of state variables. For convenience, we analyse our model in terms of proportions of quantities instead of actual populations. This can be done by scaling the population of each class by the total populations. We make the transformation 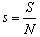
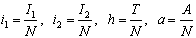 in the classes S
in the classes S 
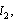 T , and A respectively.
T , and A respectively.
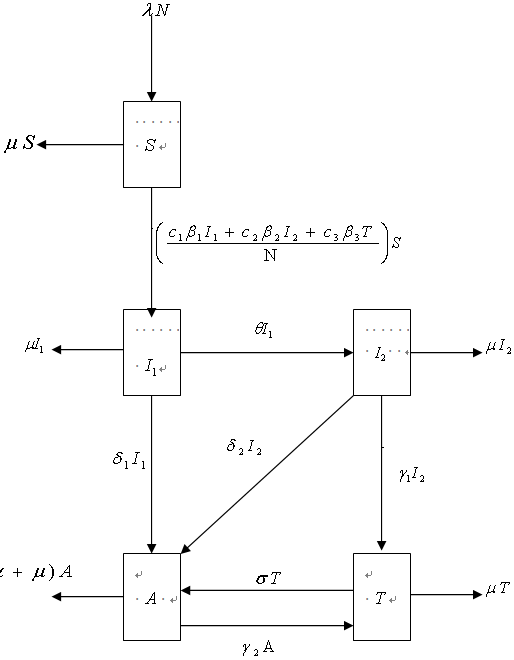 | Figure 1. A compartmental flow diagram for screening and treatment model of HIV/AIDS |
Differentiating the fractions with respect to time it is easier to verify that 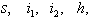 and a satisfy the following system of non-linear differential equations:
and a satisfy the following system of non-linear differential equations: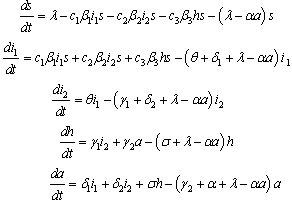 | (3) |
where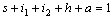 and
and 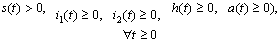 Therefore the normalised model system of equations (3) is both mathematically and epidemiologically well posed.
Therefore the normalised model system of equations (3) is both mathematically and epidemiologically well posed.
3. Model Analysis
The normalized model system of equations (3) will be analysed qualitatively to get insight into it is dynamical features which will give a better understanding of the effects of screening and treatment on the transmission of HIV/AIDS infection in a population. Threshold which governs elimination or persistence of HIV/AIDS will be determined and studied.
3.1. Disease Free Equilibrium (DFE)
The disease free equilibrium denoted by ‘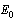 ’of the normalised model system (3) was obtained as
’of the normalised model system (3) was obtained as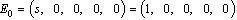 | (4) |
3.2. The Effective reproduction number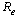
The effective reproduction number, 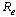 of the normalised model system (3) was obtained by using the next generation operator method and is given by
of the normalised model system (3) was obtained by using the next generation operator method and is given by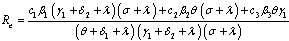 | (5) |
3.3. Numerical Sensitivity Analysis
In determining how best to reduce human mortality and morbidity due to AIDS, the sensitivity indices of the effective reproductive number ‘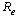 ’to the parameters in the model was calculated using approach of[13]. These indices tell us how crucial each parameter is to disease transmission and prevalence and discover parameters that have a high impact on
’to the parameters in the model was calculated using approach of[13]. These indices tell us how crucial each parameter is to disease transmission and prevalence and discover parameters that have a high impact on 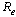 and should be targeted by intervention strategies. The normalized forward sensitivity index of a variable to a parameter is a ratio of the relative change in the variable to the relative change in the parameter. When a variable is a differentiable function of the parameter, the sensitivity index may be alternatively defined using partial derivatives.
and should be targeted by intervention strategies. The normalized forward sensitivity index of a variable to a parameter is a ratio of the relative change in the variable to the relative change in the parameter. When a variable is a differentiable function of the parameter, the sensitivity index may be alternatively defined using partial derivatives.Table 1. Numerical values of sensitivity indices of
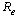 |
| | Parameter Symbol | Sensitivity Index | | 1 |
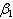
and
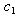
| +0.9283775048 | | 2 |
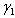
| -0.6433613445 | | 3 |
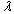
| -0.4368749246 | | 4 |
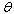
| -0.3899159664 | | 5 |
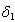
| -0.1538461538 | | 6 |
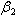
and
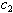
| +0.04318034906 | | 7 |
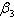
and
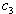
| +0.02844214609 | | 8 |
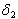
| -0.0004774833009 | | 9 |

| -0.00005677075068 |
|
|
Definition 1: The normalised forward sensitivity index of a variable ‘p’ that depends differentiable on a parameter ‘q’ is defined as: 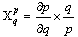 | (6) |
As we have an explicit formula for 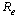 in equation (6), we derive an analytical expression for the sensitivity of
in equation (6), we derive an analytical expression for the sensitivity of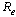 as
as  to each of parameters involved in
to each of parameters involved in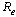 . For example the sensitivity indices of
. For example the sensitivity indices of 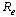 with respect to
with respect to 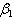 and
and 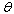 are given by;
are given by;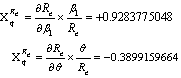 respectively. Other indices
respectively. Other indices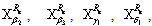
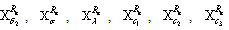 , are obtained following the same method and tabulated as follows:The parameters are ordered from most sensitive to the least.
, are obtained following the same method and tabulated as follows:The parameters are ordered from most sensitive to the least.
3.3.1. Interpretation of Sensitivity Indices
From table 1 above, generally it shows that when the parameters 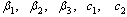 and
and 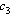 increase while the other parameters remain constant the value of
increase while the other parameters remain constant the value of 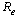 increases implying that they increase the endemicity of the disease as they have positive indices. When the parameters
increases implying that they increase the endemicity of the disease as they have positive indices. When the parameters 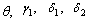 , and
, and 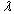 increase while keeping other parameters constant, the value of
increase while keeping other parameters constant, the value of 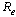 decreases, implying that they decrease the endemicity of the disease as they have negative indices.The most sensitive parameter is the contact rate of unaware HIV infective
decreases, implying that they decrease the endemicity of the disease as they have negative indices.The most sensitive parameter is the contact rate of unaware HIV infective 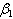 , with susceptibles followed by the rate
, with susceptibles followed by the rate 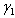 at which screened HIV infective are treated, followed by recruitment rate
at which screened HIV infective are treated, followed by recruitment rate 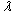 and the rate at which unaware HIV infectives
and the rate at which unaware HIV infectives 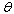 are screened. Other sensitive parameters are the rate at which unaware infectives
are screened. Other sensitive parameters are the rate at which unaware infectives 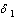 develop full blown AIDS followed by the contact rate
develop full blown AIDS followed by the contact rate 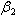 of screened HIV infective with susceptibles, the contact rate
of screened HIV infective with susceptibles, the contact rate 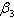 of treated infective with susceptibles and the rate
of treated infective with susceptibles and the rate 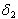 at which screened HIV infectives develop full blown AIDS respectively. The least sensitive parameter is the rate
at which screened HIV infectives develop full blown AIDS respectively. The least sensitive parameter is the rate 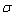 at which treated infectives develop full blown AIDS.
at which treated infectives develop full blown AIDS.
3.4. Local Stability of Disease-free Equlibrium
To determine the local stability of disease free equilibrium, the variational matrix 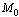 of the normalised model system (3) corresponding to disease free
of the normalised model system (3) corresponding to disease free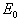 is obtained as
is obtained as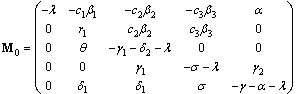 | (7) |
Where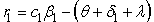 The characteristic equation corresponding to
The characteristic equation corresponding to 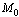 is
is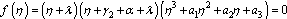 | (8) |
where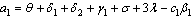
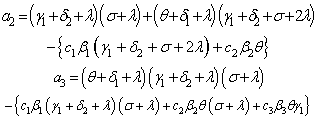 Thus according to Routh Hurwitz Criteria,
Thus according to Routh Hurwitz Criteria, 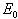 is locally asymptotically stable when
is locally asymptotically stable when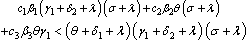 | (9) |
The condition (8) is sufficient to satisfy all the equations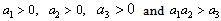 | (10) |
So it is clear that for 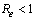 which corresponds to (9), the disease free equilibrium
which corresponds to (9), the disease free equilibrium 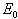 is locally asymptotically stable so that the infection does not persist in the population and under this condition the endemic equilibrium
is locally asymptotically stable so that the infection does not persist in the population and under this condition the endemic equilibrium 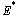 does not exist. It is unstable for
does not exist. It is unstable for 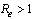 and then
and then 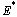 exists and the infection is maintained in the population.This situation can also be realised easily when we try to assess the contribution of
exists and the infection is maintained in the population.This situation can also be realised easily when we try to assess the contribution of 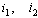 and h in terms of
and h in terms of 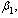
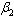 and
and 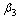 respectively from equation (5) above.Let
respectively from equation (5) above.Let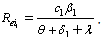 | (11) |
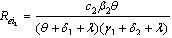 | (12) |
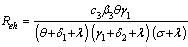 | (13) |
where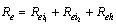 | (14) |
From the equations (11)-(13) above, it is clear that 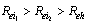 which implies that unaware infectives ‘
which implies that unaware infectives ‘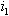 ’ are the ones contributing the most on the transmission of the HIV/AIDS infection followed by screened infectives ‘
’ are the ones contributing the most on the transmission of the HIV/AIDS infection followed by screened infectives ‘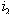 ’which keeps the disease endemic (i.e.
’which keeps the disease endemic (i.e. 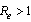 ) in the population via
) in the population via 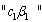 and
and 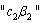 respectively compared to treated individuals ‘h’ via
respectively compared to treated individuals ‘h’ via 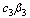 . In the absence of infection, the population size approaches the steady state
. In the absence of infection, the population size approaches the steady state 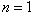 for normalised model system (3) and
for normalised model system (3) and 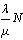 for the original model system (1). However when the disease remain endemic the disease induced deaths reduce the equilibrium population size from
for the original model system (1). However when the disease remain endemic the disease induced deaths reduce the equilibrium population size from 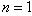 to
to 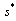 .
.
3.5. Endemic Equilibrium (EEP) and Local Stability
The endemic equilibrium of the normalised model system (3) is given by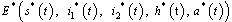 which exists for
which exists for 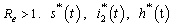 and
and 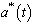 are expressed in terms of
are expressed in terms of 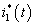 which satisfies the following relations:
which satisfies the following relations: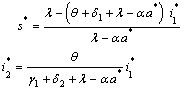 | (15) |
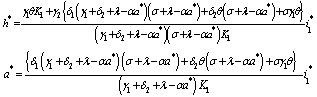 and
and 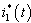 is the solution of the following quadratic polynomial
is the solution of the following quadratic polynomial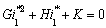 | (16) |
where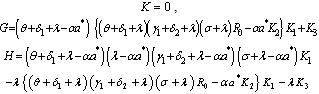 and
and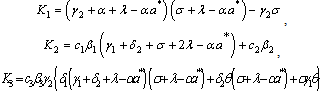 From equation (16) it follows that
From equation (16) it follows that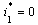 which corresponds to the disease free equilibrium already being discussed or
which corresponds to the disease free equilibrium already being discussed or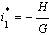 , which gives
, which gives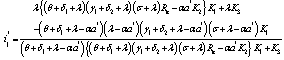 | (17) |
corresponding to unique endemic equilibrium 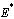 when
when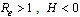 and
and 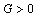 .From this result we state the following theorem which will be proved by using bifurcation diagram and Centre Manifold theorem.Theorem.3.1. The unique endemic equilibrium
.From this result we state the following theorem which will be proved by using bifurcation diagram and Centre Manifold theorem.Theorem.3.1. The unique endemic equilibrium 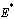 exists if
exists if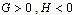 and
and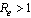 , and is locally stable if
, and is locally stable if 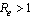 and unstable if
and unstable if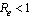 .
.
3.5.1. Determination of Forward or Backward Bifurcation
From equation (16), it follows that there is no backward bifurcation since the value of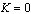 , hence no multiple equilibria. Therefore existence of unique endemic equilibrium which is locally stable for
, hence no multiple equilibria. Therefore existence of unique endemic equilibrium which is locally stable for 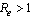 and unstable if
and unstable if 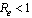 was explored by a forward bifurcation diagram obtained when a graph of proportion of unaware infective ‘
was explored by a forward bifurcation diagram obtained when a graph of proportion of unaware infective ‘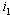 ’against reproduction number ‘
’against reproduction number ‘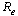 ’ was sketched as shown below:
’ was sketched as shown below: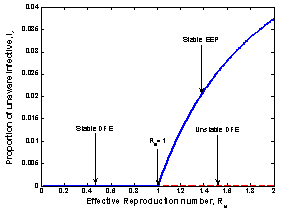 | Figure 2. The figure of proportion of unaware infective ‘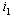 ’ versus effective reproduction number ’ versus effective reproduction number 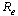 |
Figure 2 exhibit a forward bifurcation when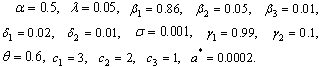 In figure 2 above, the two equilibrium points exchange stabilities depending on the value of
In figure 2 above, the two equilibrium points exchange stabilities depending on the value of 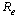 . A transcritical/forward bifurcation in the equilibrium points occur at
. A transcritical/forward bifurcation in the equilibrium points occur at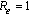 . If
. If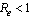 , no biologically meaningful endemic equilibrium solution exists and the disease free equilibrium is the only local attractor. But if
, no biologically meaningful endemic equilibrium solution exists and the disease free equilibrium is the only local attractor. But if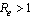 , the endemic equilibrium exists and it is the only local attractor while the disease free equilibrium is a saddle point. Thus there is a forward bifurcation because in the neighbourhood of the bifurcation point, the endemic disease prevalence (proportion of unaware infectives
, the endemic equilibrium exists and it is the only local attractor while the disease free equilibrium is a saddle point. Thus there is a forward bifurcation because in the neighbourhood of the bifurcation point, the endemic disease prevalence (proportion of unaware infectives 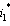 ) is an increasing function of
) is an increasing function of 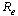 as shown in equation (17).The local asymptotic stability of endemic equilibrium is analyzed by using the Centre Manifold theory[14] and shows that it is stable under certain conditions. The normalised model system (3) shows that it will exhibit a backward bifurcation which occurs at
as shown in equation (17).The local asymptotic stability of endemic equilibrium is analyzed by using the Centre Manifold theory[14] and shows that it is stable under certain conditions. The normalised model system (3) shows that it will exhibit a backward bifurcation which occurs at 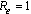 under certain condition otherwise it will exhibit a forward bifurcation at
under certain condition otherwise it will exhibit a forward bifurcation at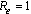 as shown in figure 2 and is locally stable.
as shown in figure 2 and is locally stable.
3.6. Global Stability of Endemic Equilibrium
Theorem 3.3 If 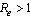 the endemic equilibrium
the endemic equilibrium 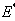 of the normalised model system (3) is globally asymptotically stable.Proof To establish the global stability of endemic equilibrium
of the normalised model system (3) is globally asymptotically stable.Proof To establish the global stability of endemic equilibrium 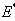 we construct the following positive Lyapunov function V as follows:
we construct the following positive Lyapunov function V as follows: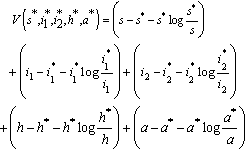 | (18) |
By direct calculation of the derivative of V along the solutions of (3) we have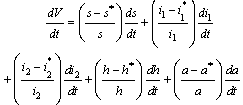 | (19) |
which gives 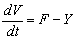 | (20) |
where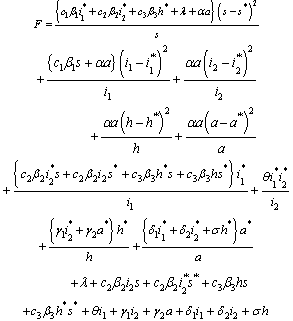 and
and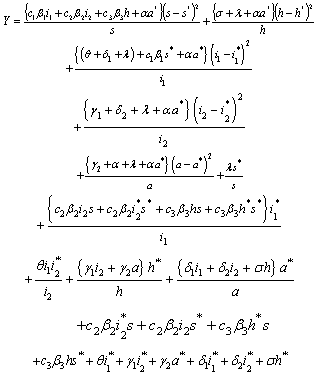 Thus from equation (20), if
Thus from equation (20), if 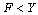 then
then 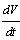 will be negative definite, meaning that
will be negative definite, meaning that 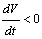 Also it follows that
Also it follows that 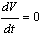 if and only if
if and only if 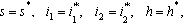
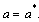 Therefore the largest compact invariant set in
Therefore the largest compact invariant set in 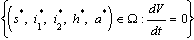 is the singleton
is the singleton 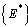 where
where 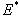 is the endemic equilibrium of the normalised model system (3). By LaSalles’s invariant principle, then it implies that
is the endemic equilibrium of the normalised model system (3). By LaSalles’s invariant principle, then it implies that 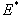 is globally asymptotically stable in
is globally asymptotically stable in 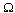 if
if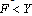 .
.
3.7. Model with Screening and Treatment When Treated HIV Infectives do not Transmit the Infection in a Population 
In this case, we consider the situation where the treated HIV infectives take the preventive measures and change their behaviour so as not to transmit the infection by sexual interaction in the community  . Thus the infection is transmitted by those infectives who are not aware of their infection and those who are screened only (not using ARV). The basic reproduction number in this case is given by
. Thus the infection is transmitted by those infectives who are not aware of their infection and those who are screened only (not using ARV). The basic reproduction number in this case is given by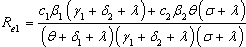 and we note that
and we note that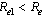 . We also note that
. We also note that 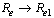 as
as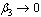 . Therefore we can conclude that the endemicity of the infection is reduced when the treated HIV infectives present a positive attitude towards preventive measures and do not take part in the transmission of the disease.
. Therefore we can conclude that the endemicity of the infection is reduced when the treated HIV infectives present a positive attitude towards preventive measures and do not take part in the transmission of the disease.
3.8. Model with Screening and Treatment When Both Screened and Treated HIV Infectives Respectively do not Transmit the Infection in a Population 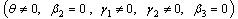
In this case, we consider the situation where both the screened and treated HIV infectives respectively take the preventive measures and change their behaviours so as not to transmit the infection by sexual interaction in the community 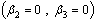 Thus the infection is transmitted only by those infectives who are not aware of their infections. The basic reproduction number in this case is given by
Thus the infection is transmitted only by those infectives who are not aware of their infections. The basic reproduction number in this case is given by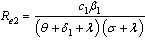 and we note that
and we note that 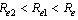 and
and 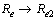 as
as 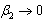 and
and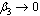 . Therefore we can conclude that the endemicity of the infection is reduced when screened and treated HIV infectives both reflect a positive attitude towards preventive measures and do not take part in the transmission of the disease.
. Therefore we can conclude that the endemicity of the infection is reduced when screened and treated HIV infectives both reflect a positive attitude towards preventive measures and do not take part in the transmission of the disease.
3.9. Model in the Absence of Treatment (Screening only, 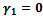 and
and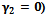
Here we consider the situation where there is no ARV treatment for the screened HIV infectives 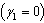 and AIDS population who are not treated
and AIDS population who are not treated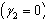 . The normalized model system (3) for this case is reduced to the group of proportion of susceptibles, unaware infectives, screened infectives and AIDS class population. As there is no treatment, i.e.
. The normalized model system (3) for this case is reduced to the group of proportion of susceptibles, unaware infectives, screened infectives and AIDS class population. As there is no treatment, i.e. 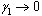 and
and 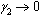 then
then 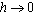 we obtain the basic reproduction number
we obtain the basic reproduction number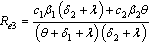 We note that
We note that 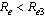 and
and  as,
as, 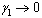 and
and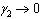 . Therefore we can conclude that the endemicity of the infection in this case increases in the absence of treatment with ARV for the screened infectives and AIDS population.
. Therefore we can conclude that the endemicity of the infection in this case increases in the absence of treatment with ARV for the screened infectives and AIDS population.
3.10. Model in the Absence of Screening 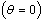
Here we consider the situation without screening of unaware infectives. In this case the normalised model system (3) is reduced to the group of proportion of susceptibles, unaware infectives and AIDS class population. As there is no screening of unaware infectives, then 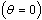 . This Implies that
. This Implies that 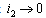 and
and 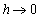 in which case we obtain the basic reproduction number as
in which case we obtain the basic reproduction number as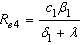 We note that
We note that 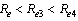 and
and 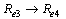 as
as 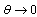 .Therefore we can conclude that the endemicity of the infection in this case increases in the absence of detection of unaware infectives by screening.By analysing the four epidemiological situations discussed above, it may be concluded that in the presence of screening and treatment, if both the screened and treated HIV infectives decide to take preventive measures and do not transmit the infection, the disease will tend to the endemic state if both the screening and treatment rates are small. If the annual screening and treatment rates are very high (say 99% of the initial population), the disease may tend to disease free equilibrium point. However if screened and treated HIV infectives also contribute to the transmission of the disease, then even if both screening and treatment rates are very high, the disease is set up among the population as the system continues towards asymptotically stable endemic equilibrium point. Analysis also shows that the endemicity of the disease is reduced by screening of unaware HIV infectives and treatment of the screened HIV infectives in the population.
.Therefore we can conclude that the endemicity of the infection in this case increases in the absence of detection of unaware infectives by screening.By analysing the four epidemiological situations discussed above, it may be concluded that in the presence of screening and treatment, if both the screened and treated HIV infectives decide to take preventive measures and do not transmit the infection, the disease will tend to the endemic state if both the screening and treatment rates are small. If the annual screening and treatment rates are very high (say 99% of the initial population), the disease may tend to disease free equilibrium point. However if screened and treated HIV infectives also contribute to the transmission of the disease, then even if both screening and treatment rates are very high, the disease is set up among the population as the system continues towards asymptotically stable endemic equilibrium point. Analysis also shows that the endemicity of the disease is reduced by screening of unaware HIV infectives and treatment of the screened HIV infectives in the population.
4. Numerical Simulations
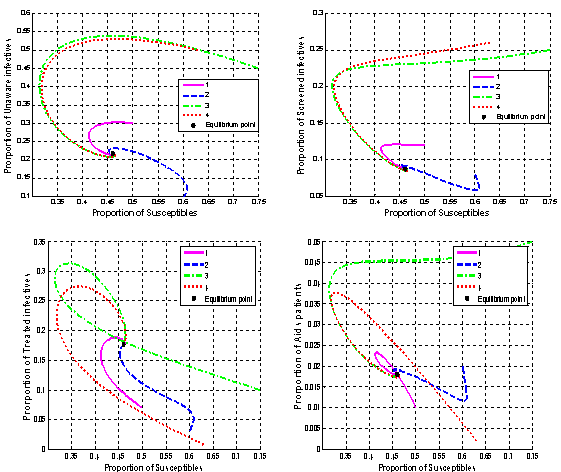 | Figure 4.1. Variation of proportion of infective classes’ population and proportion of AIDS patients’ population against proportion of susceptibles population |
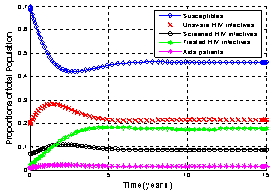 | Figure.4.2. Variation of proportion of total population in different classes |
In order to illustrate the analytical results of the study, numerical simulations of the normalised model system (3) are carried out using the set of estimated parameter values below: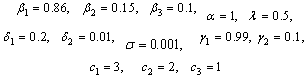 | (21) |
However this parameters may (or may not) be biologically feasible.Figures 4.1. below show the proportion of HIV infective populations (unaware, screened and treated) and proportion of AIDS infectives all plotted against the proportion of susceptible population. This shows the dynamic behaviour of the endemic equilibrium of the normalised model system (3) using the parameter values in equation (21) for different initial starting values in four cases as shown below. The equilibrium points of the endemic equilibrium
The equilibrium points of the endemic equilibrium 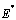 was obtained as
was obtained as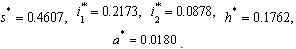 It is seen from these figures that for any starting initial value, the solution curves tend to the equilibrium
It is seen from these figures that for any starting initial value, the solution curves tend to the equilibrium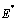 . Therefore we conclude that the normalised model system (3) is globally stable about this endemic equilibrium point
. Therefore we conclude that the normalised model system (3) is globally stable about this endemic equilibrium point 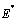 for the estimated parameters above.Figure .4.2 below show the variation of the proportion of total population in all classesIt is seen that the proportion of susceptible population decreases with time and then reaches its equilibrium position. This is due to treatment with ARV. Therefore infection becomes less endemic in the population. Initially proportion of unaware infectives increases but due to the increase in screening and treatment, the rates
for the estimated parameters above.Figure .4.2 below show the variation of the proportion of total population in all classesIt is seen that the proportion of susceptible population decreases with time and then reaches its equilibrium position. This is due to treatment with ARV. Therefore infection becomes less endemic in the population. Initially proportion of unaware infectives increases but due to the increase in screening and treatment, the rates 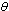 and
and 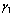 respectively, decreases then reaches its equilibrium position. This ultimately leads to the decrease of the proportion of AIDS infectives.In figures 4.3-4.4, the variation of proportions of susceptible, unaware, screened and treated HIV infective populations and proportion of AIDS patient population for different rates of screening is shown
respectively, decreases then reaches its equilibrium position. This ultimately leads to the decrease of the proportion of AIDS infectives.In figures 4.3-4.4, the variation of proportions of susceptible, unaware, screened and treated HIV infective populations and proportion of AIDS patient population for different rates of screening is shown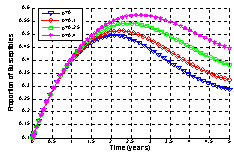 | Figure .4.3. Variation of proportion of susceptible population for different values of  |
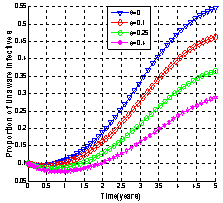 | Figure 4.4(i). Variation of proportion of unaware infectives for different values of  |
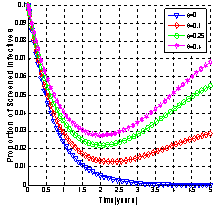 | Figure 4.4(ii). Variation of proportion of screened infectives for different values of 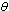 |
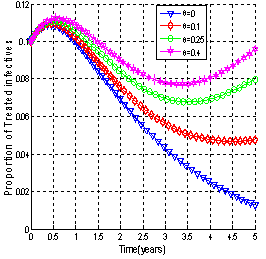 | Figure 4.4(iii). Variation of proportion of treated infectives for different values of 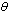 |
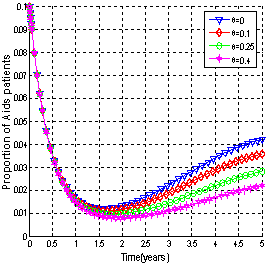 | Figure 4.4(iv). Variation of proportion of AIDS patients for different values of 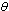 |
It is seen that as the screening rate increases, the proportion of susceptible population increases (Figure 4.3). From Figure 4.4 (i), it is seen that the unaware HIV infectives become aware of their infection which results in the decrease of the proportion of unaware infectives population and increase in the proportions of screened and treated HIV infectives (Figure 4.4 (ii) and (iii)) respectively. This ultimately leads to decrease of the proportion of AIDS infected population as shown in Figure 4.4 (iv) above. Thus as the screening rate becomes zero, the unaware infectives will continue maintaining sexual relationships in the community leading to the increase in the proportion of AIDS infective population.Figures 4.5 - 4.6 show the variation of proportions of susceptibles, unaware, screened and treated HIV infectives and proportion of AIDS patients population for different rates of treatment.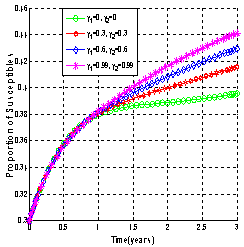 | Figure 4.5(i). Variation of proportion of Susceptible population for different values of 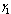 and and 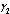 |
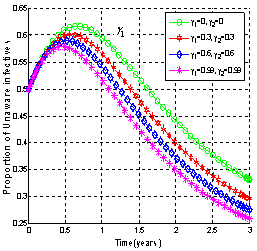 | Figure 4.5(ii). Variation of proportion of unaware infectives for different values of 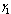 and and 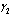 |
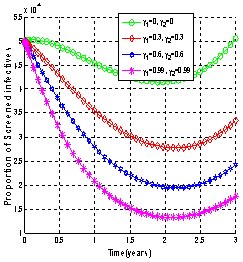 | Figure 4.5(iii). Variation of proportion of screened infectives for different values of 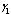 and and 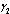 |
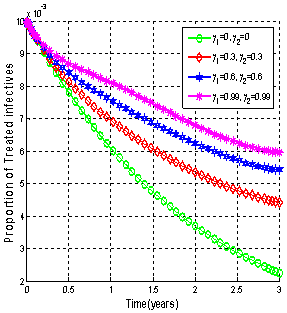 | Figure 4.5(iv). Variation of proportion of treated infectives for different values of 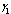 and and 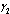 |
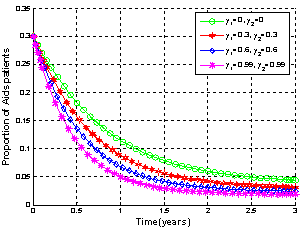 | Figure.4.6. Variation of proportion of AIDS patient’s population for different values of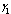 and and 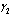 |
It is seen that as the treatment rate increases, the proportion of susceptible population increases (Figure4.5 (i)). The screened HIV infectives decided to use ARV treatment which results in the decrease of the proportion of screened infective population (Figure 4.5 (iii)) leading to the increase in the proportion of the treated HIV infective population (Figure 4.5 (iv)). This ultimately leads to decrease the proportion of unaware infective population (Figure4.5 (ii)) leading to decrease the proportion of AIDS patient’s population (Figure 4.6). Thus as the treatment rate becomes zero, the proportion of unaware and screened HIV infectives population increases (Figure4.5 (ii) and (iii)) respectively leading to the increase in proportion of AIDS patients population (Figure 4.6).Figures 4.7 shows the role of contact rates 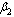 and
and 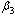 of the screened and treated HIV infectives respectively.
of the screened and treated HIV infectives respectively. | Figure 4.7(i). Variation of proportion of unaware infectives for different values of 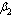 and and 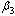 respectively. respectively. |
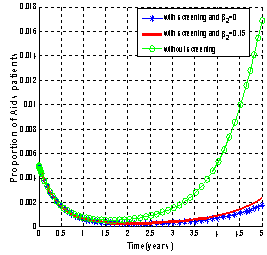 | Figure 4.7(ii). Variation of proportion of AIDS patients for different values of 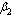 and and 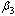 respectively. respectively. |
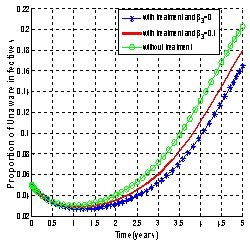 | Figure 4.7(iii). Variation of proportion of unaware infectives for different values of 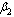 and and 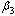 respectively. respectively. |
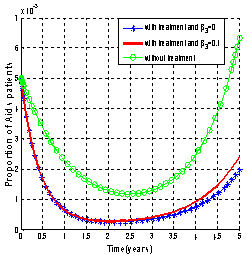 | Figure 4.7(iv). Variation of proportion of AIDS patients for different values of 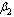 and and 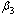 respectively. respectively. |
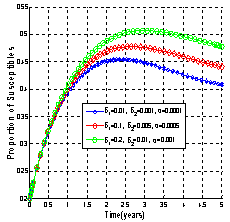 | Figure 4.8(i). Variation of proportion of susceptibles for different values of 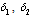 , and , and 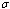 |
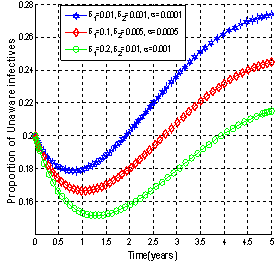 | Figure 4.8(ii). Variation of proportion of unaware infectives for different values of 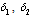 and and 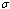 |
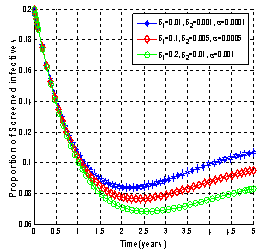 | Figure 4.8(iii). Variation of proportion of screened infectives for different values of 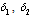 and and 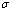 |
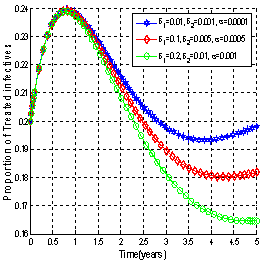 | Figure 4.8(iv). Variation of proportion of treated infectives for different values of 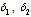 and and 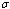 |
 | Figure 4.9. Variation of proportion of AIDS patients population for different values of 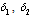 and and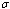 . . |
It can be observed that as screened and treated HIV infectives choose to participate in sexual interactions without exposing themselves, the proportion of unaware HIV infective population increases which in turn increases the proportion of AIDS patients population. When screened and treated HIV infectives do not take part in sexual interactions, means that 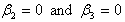 respectively and the proportion of unaware HIV infectives decreases leading to the decrease of proportion of AIDS patients population. From these figures, it is also clear that in the absence of screening of unaware HIV infectives and treatment of screened HIV infectives, the higher proportion of unaware and screened HIV infectives respectively leads to increase of the proportion of AIDS patients population. Thus to keep the transmission of the epidemic under control, the screened and treated HIV infectives individuals should be counselled to either abstain from sexual interaction or use preventive measures like condoms to stop transmitting HIV infection.
respectively and the proportion of unaware HIV infectives decreases leading to the decrease of proportion of AIDS patients population. From these figures, it is also clear that in the absence of screening of unaware HIV infectives and treatment of screened HIV infectives, the higher proportion of unaware and screened HIV infectives respectively leads to increase of the proportion of AIDS patients population. Thus to keep the transmission of the epidemic under control, the screened and treated HIV infectives individuals should be counselled to either abstain from sexual interaction or use preventive measures like condoms to stop transmitting HIV infection. | Figure 4.10(i). Variation of proportion of AIDS patients population for different values of 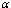 |
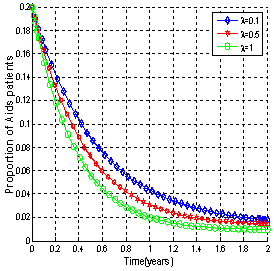 | Figure 4.10(ii). Variation of proportion of AIDS patients population for different values of 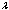 |
Figures.4.8 - 4.9 show the variations of proportions of susceptibles, HIV infective classes and AIDS patients population with time for different values of movement rates 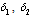 and
and 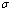 of unaware, screened and treated infectives respectively.It is seen that as the movement rates from infective classes increases, proportions of all infective classes populations decreases (Figures 4.8 (ii), (iii) and (iv)) which in turn increases the proportion of AIDS patients population (Figure.4.9) and also increases the proportion of susceptible population (Figure 4.8 (i)).Figures 4.10 show the variation of proportion of AIDS patients population for different values of disease induced death rate
of unaware, screened and treated infectives respectively.It is seen that as the movement rates from infective classes increases, proportions of all infective classes populations decreases (Figures 4.8 (ii), (iii) and (iv)) which in turn increases the proportion of AIDS patients population (Figure.4.9) and also increases the proportion of susceptible population (Figure 4.8 (i)).Figures 4.10 show the variation of proportion of AIDS patients population for different values of disease induced death rate 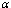 and recruitment rate
and recruitment rate 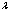 of susceptibles respectively.It is observed from the figures that as
of susceptibles respectively.It is observed from the figures that as 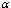 increases the proportion of AIDS patients population decreases and it is also observed that as the recruitment rate increases, the proportion of AIDS patient population increases.
increases the proportion of AIDS patients population decreases and it is also observed that as the recruitment rate increases, the proportion of AIDS patient population increases.
5. Discussion and Conclusions
A non linear mathematical model has been proposed and analyzed to study the effect of screening of unaware HIV infectives and treatment of screened HIV infectives on the transmission of HIV/AIDS infection in a population. The disease free and endemic equilibria were obtained and their stabilities investigated. The model showed that the disease free equilibrium is locally stable by using Routh Hurwitz criteria at threshold parameter less than unity and unstable at threshold parameter greater than unity, but globally the disease free equilibrium is not stable due existence of forward bifurcation at threshold parameter equal to unity. Also the model analysis showed the existence of unique endemic equilibrium that is locally stable under certain conditions when the threshold parameter exceeds unity due to existence of forward bifurcation at threshold parameter equal to unity. Using Lyapunov method, endemic equilibrium is globally stable under certain conditions. A sensitivity analysis shows that ‘’ is the most sensitive parameter on and the least is ‘ A numerical study of the model was carried out to see the effect of key parameters on the transmission of HIV/AIDS infections. The analysis shows that the screening of unaware HIV infectives and treatment of screened HIV infectives have the effect of reducing the transmission of the disease. It is observed that when the screened infectives and treated infectives do not participate in the transmission of the infection, the AIDS population is significantly reduced in comparison to the case where there is no screening and treatment. It is found that the disease becomes more endemic in the absence of screening and treatment and consequently the AIDS population increase. This has a consequence of people not knowing that they are infected and still practice sexual relationships without taking precautions. Screening makes people aware of their infection and reduce their viral load by using ARV treatment and consequently AIDS patients population decreases. This is due to the fact that on being aware of their infection and using ARV, people either abstain to interact sexually or use preventive measures like using condoms and by changing their behaviour which results in the decline of AIDS epidemic.Based on the results of the study, we conclude that the most effective way to reduce the transmission of HIV and AIDS epidemic infection is to educate people to go for voluntary HIV screening and become aware of their HIV status and if an individual finds himself/herself HIV positive, then he/she has to be willing to undergo ARV treatment and therapy so as to reduce the viral load hence prolonging life. Furthermore people should be educated to be aware of the consequences of practising unsafe sex and other preventive measures against the infection. If the population shows positive attitude towards voluntary screening, treatment with ARV and preventive procedures, then the transmission of the disease can be controlled. Therefore the national HIV/AIDS control programs for all developing countries should increase the education programs on the importance of voluntary HIV screening, ARV treatment and preventive procedures to the community at all social classes especially lower classes and high risk groups so that the transmission of the disease can be controlled. Finally, more HIV/AIDS centres for voluntary screening and ARV treatment should be established across each country to ensure that more people have access to the facilities hence reducing the transmission of HIV and therefore reduce the AIDS epidemic.
References
| [1] | A. Tripathi, R. Naresh, D. Sharma, Modelling the effect of screening of Unaware invectives on the spread of HIV infection. Science Direct. Applied Mathematics and Computation, (2007), 184.1053-1068, 2007. |
| [2] | J.Y.T. Mugisha, L.S. Luboobi, The Effect of Vaccinating Susceptible Adults against HIV/AIDS in a Two- Age Groups Population. Zim. J. Sc. Tech. Vol. 1(2): 91 – 103, 2000. |
| [3] | V.D. Lima, K. Johnston, S.R. Hogg, A.R Levy, P.R. Harrigan, A. Anema, J.S.G. Montaner, Expanded access to Highly Active Antiretroviral Therapy: A Potentially powerful strategy to curb down the growth of HIV epidemic, America Journal of Infectious Disease 198, 59-67, 2008. |
| [4] | R.M. Granich, C. F. Gilks, C. Dye, K.M. Decock, B.G. William, (2008), Universal Voluntary HIV testing with immediate antiretroviral therapy as a strategy for elimination of HIV transmission, Lancet, 373: 48–57, 2009. |
| [5] | R. M. Anderson, G. F. Medly, R. M. May, A. M. Johnson, A preliminary study of the transmission dynamics of the Human Immunodeficiency Virus (HIV), the causative agent of AIDS, IMA J. Math. Appl. Med. Biol., 3: 229-263,1986. |
| [6] | R. M. Anderson and R. M. May Infectious Diseases of Human Dynamics and Control. Oxford University press, Oxford, 1991. |
| [7] | R. M. Anderson, The role of mathematical models in the study of HIV transmission and the epidemiology of AIDS, J. AIDS 1: 241-256, 1988. |
| [8] | H. W. Hethcote, J. W. Van Ark, Modelling HIV Transmission and AIDS in the United States, in: Lect. Notes Biomath, Vol. 95, Springer, Berlin, 1992. |
| [9] | A. S. Perelson, P. W. Nelson, Mathematical analysis of HIV-1 dynamics in vivo, SIAM Rev., 41 (1): 3-44, 1999. |
| [10] | C. C. McCluskey, A model of HIV/AIDS with staged progression and amelioration, Math. Biosci., 181: 1-16, 2003. |
| [11] | Y-H. Hsieh, C.H. Chen, Modelling the social dynamics of a sex industry: Its implications for spread of HIV/AIDS, Bull. Math. Biol., 66: 143-166, 2004. |
| [12] | S. Issa, Modelling the effect of screening on the spread of HIV infection in a Homogeneous population with infective immigrants. M.Sc Dissertation University of Dar-es-salaam, 2010. |
| [13] | [N. Chitnis, J. M. Hyman, J. M. Cushing, Determining Important Parameters in the Spread of Malaria Through the Sensitivity Analysis of a Mathematical Model, Bulletin of Mathematical Biology, (2008), DOI10.1007/s11538-008-9299-0, 2008. |
| [14] | M. G. M. Gomes, L. J. White, G. F. Medley, Infection, Reinfection, and Vaccination Under Suboptimal Immune Protection: Epidemiological Perspectives, J. Theor. Biol. 228, p. 539-549, 2004. |

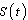 ’, Unaware infectives ‘
’, Unaware infectives ‘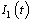 ’, Screened infectives ‘
’, Screened infectives ‘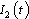 ’, Treated class ‘
’, Treated class ‘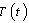 ’ and Full blown AIDS class ‘
’ and Full blown AIDS class ‘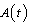 ’. The susceptibles are individuals that have not contracted the HIV infection (HIV negative); the unaware infectives are individuals that have contracted the HIV infection but are not aware of their infection; the screened infectives are individuals that have contracted the HIV infection and are known to be infected after being detected by a medical screening method, treated class (not cured but undergoing treatment) are individuals who use ARV(anti retrovirus) therapy after being screened and become screened infectives or develop full blown AIDS.In formulating the model, the following assumptions are taken into consideration:(i) The rate of transmission is direct proportional to the susceptibles population and also to the ratio between the members of infected population to the total population.(ii) Only screened infectives and full blown AIDS can be treated with ARV therapy (i.e. can move to treated class) at different rates
’. The susceptibles are individuals that have not contracted the HIV infection (HIV negative); the unaware infectives are individuals that have contracted the HIV infection but are not aware of their infection; the screened infectives are individuals that have contracted the HIV infection and are known to be infected after being detected by a medical screening method, treated class (not cured but undergoing treatment) are individuals who use ARV(anti retrovirus) therapy after being screened and become screened infectives or develop full blown AIDS.In formulating the model, the following assumptions are taken into consideration:(i) The rate of transmission is direct proportional to the susceptibles population and also to the ratio between the members of infected population to the total population.(ii) Only screened infectives and full blown AIDS can be treated with ARV therapy (i.e. can move to treated class) at different rates 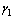 and
and 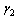 respectively.(iii) Unaware infectives, screened infectives and treated class will move to full blown AIDS at different rates
respectively.(iii) Unaware infectives, screened infectives and treated class will move to full blown AIDS at different rates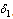 ,
, 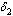 and
and 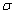 respectively where
respectively where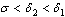 . (iv) Unaware infectives can only move to screened class and full blown AIDS and unaware infective can be screened at a rate ‘
. (iv) Unaware infectives can only move to screened class and full blown AIDS and unaware infective can be screened at a rate ‘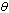 ’.(v) Unaware infectives, screened infectives and treated class can infect susceptibles class at different rates
’.(v) Unaware infectives, screened infectives and treated class can infect susceptibles class at different rates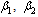 and
and 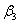 respectively where
respectively where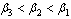 .Following mixing of susceptibles, unaware infectives, screened infectives, treated class and full blown AIDS patients, susceptibles acquire HIV infection with the force of infection
.Following mixing of susceptibles, unaware infectives, screened infectives, treated class and full blown AIDS patients, susceptibles acquire HIV infection with the force of infection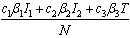 . The population considered to be homogeneously mixed and each susceptible individual has equal chance of acquiring HIV infection when comes into contact with infectious individual. The population under study comprises of persons with at least 15 years, so in this case it is assumed that there is no vertical transmission and all recruitment are natural birth without disease, population is variable and all parameters are positive. Taking into account the above considerations, we then have the following schematic flow diagram:
. The population considered to be homogeneously mixed and each susceptible individual has equal chance of acquiring HIV infection when comes into contact with infectious individual. The population under study comprises of persons with at least 15 years, so in this case it is assumed that there is no vertical transmission and all recruitment are natural birth without disease, population is variable and all parameters are positive. Taking into account the above considerations, we then have the following schematic flow diagram: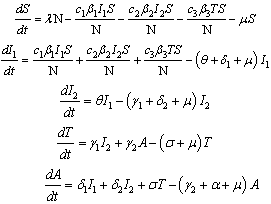
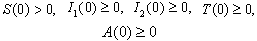 The total population at time is given by,This gives
The total population at time is given by,This gives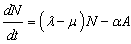
 declines for
declines for  and grows exponentially for
and grows exponentially for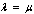 . So we shall assume that mortality rate
. So we shall assume that mortality rate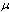 , will be a function of state variables. For convenience, we analyse our model in terms of proportions of quantities instead of actual populations. This can be done by scaling the population of each class by the total populations. We make the transformation
, will be a function of state variables. For convenience, we analyse our model in terms of proportions of quantities instead of actual populations. This can be done by scaling the population of each class by the total populations. We make the transformation 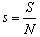
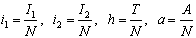 in the classes S
in the classes S 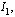
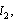 T , and A respectively.
T , and A respectively.
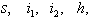 and a satisfy the following system of non-linear differential equations:
and a satisfy the following system of non-linear differential equations: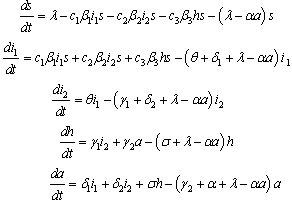
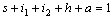 and
and 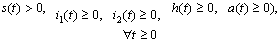 Therefore the normalised model system of equations (3) is both mathematically and epidemiologically well posed.
Therefore the normalised model system of equations (3) is both mathematically and epidemiologically well posed. ’of the normalised model system (3) was obtained as
’of the normalised model system (3) was obtained as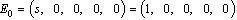
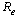
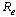 of the normalised model system (3) was obtained by using the next generation operator method and is given by
of the normalised model system (3) was obtained by using the next generation operator method and is given by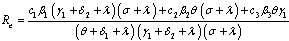
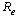 ’to the parameters in the model was calculated using approach of[13]. These indices tell us how crucial each parameter is to disease transmission and prevalence and discover parameters that have a high impact on
’to the parameters in the model was calculated using approach of[13]. These indices tell us how crucial each parameter is to disease transmission and prevalence and discover parameters that have a high impact on 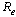 and should be targeted by intervention strategies. The normalized forward sensitivity index of a variable to a parameter is a ratio of the relative change in the variable to the relative change in the parameter. When a variable is a differentiable function of the parameter, the sensitivity index may be alternatively defined using partial derivatives.
and should be targeted by intervention strategies. The normalized forward sensitivity index of a variable to a parameter is a ratio of the relative change in the variable to the relative change in the parameter. When a variable is a differentiable function of the parameter, the sensitivity index may be alternatively defined using partial derivatives.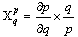
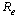 in equation (6), we derive an analytical expression for the sensitivity of
in equation (6), we derive an analytical expression for the sensitivity of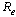 as
as  to each of parameters involved in
to each of parameters involved in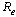 . For example the sensitivity indices of
. For example the sensitivity indices of 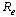 with respect to
with respect to 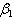 and
and 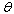 are given by;
are given by;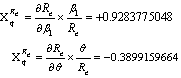 respectively. Other indices
respectively. Other indices
 , are obtained following the same method and tabulated as follows:The parameters are ordered from most sensitive to the least.
, are obtained following the same method and tabulated as follows:The parameters are ordered from most sensitive to the least. and
and 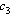 increase while the other parameters remain constant the value of
increase while the other parameters remain constant the value of 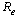 increases implying that they increase the endemicity of the disease as they have positive indices. When the parameters
increases implying that they increase the endemicity of the disease as they have positive indices. When the parameters 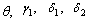 , and
, and 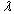 increase while keeping other parameters constant, the value of
increase while keeping other parameters constant, the value of 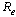 decreases, implying that they decrease the endemicity of the disease as they have negative indices.The most sensitive parameter is the contact rate of unaware HIV infective
decreases, implying that they decrease the endemicity of the disease as they have negative indices.The most sensitive parameter is the contact rate of unaware HIV infective 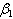 , with susceptibles followed by the rate
, with susceptibles followed by the rate 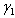 at which screened HIV infective are treated, followed by recruitment rate
at which screened HIV infective are treated, followed by recruitment rate 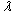 and the rate at which unaware HIV infectives
and the rate at which unaware HIV infectives 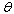 are screened. Other sensitive parameters are the rate at which unaware infectives
are screened. Other sensitive parameters are the rate at which unaware infectives 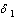 develop full blown AIDS followed by the contact rate
develop full blown AIDS followed by the contact rate 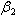 of screened HIV infective with susceptibles, the contact rate
of screened HIV infective with susceptibles, the contact rate 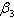 of treated infective with susceptibles and the rate
of treated infective with susceptibles and the rate 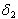 at which screened HIV infectives develop full blown AIDS respectively. The least sensitive parameter is the rate
at which screened HIV infectives develop full blown AIDS respectively. The least sensitive parameter is the rate 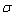 at which treated infectives develop full blown AIDS.
at which treated infectives develop full blown AIDS.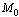 of the normalised model system (3) corresponding to disease free
of the normalised model system (3) corresponding to disease free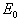 is obtained as
is obtained as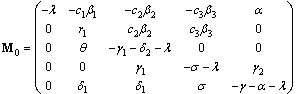
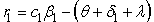 The characteristic equation corresponding to
The characteristic equation corresponding to 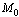 is
is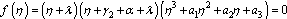
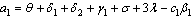
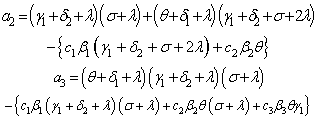 Thus according to Routh Hurwitz Criteria,
Thus according to Routh Hurwitz Criteria, 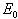 is locally asymptotically stable when
is locally asymptotically stable when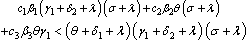
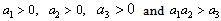
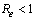 which corresponds to (9), the disease free equilibrium
which corresponds to (9), the disease free equilibrium 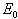 is locally asymptotically stable so that the infection does not persist in the population and under this condition the endemic equilibrium
is locally asymptotically stable so that the infection does not persist in the population and under this condition the endemic equilibrium 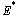 does not exist. It is unstable for
does not exist. It is unstable for 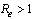 and then
and then 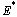 exists and the infection is maintained in the population.This situation can also be realised easily when we try to assess the contribution of
exists and the infection is maintained in the population.This situation can also be realised easily when we try to assess the contribution of 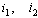 and h in terms of
and h in terms of 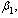
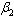 and
and 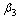 respectively from equation (5) above.Let
respectively from equation (5) above.Let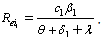
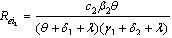
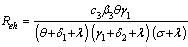
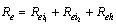
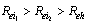 which implies that unaware infectives ‘
which implies that unaware infectives ‘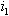 ’ are the ones contributing the most on the transmission of the HIV/AIDS infection followed by screened infectives ‘
’ are the ones contributing the most on the transmission of the HIV/AIDS infection followed by screened infectives ‘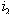 ’which keeps the disease endemic (i.e.
’which keeps the disease endemic (i.e. 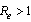 ) in the population via
) in the population via 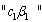 and
and 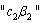 respectively compared to treated individuals ‘h’ via
respectively compared to treated individuals ‘h’ via 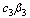 . In the absence of infection, the population size approaches the steady state
. In the absence of infection, the population size approaches the steady state 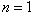 for normalised model system (3) and
for normalised model system (3) and 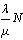 for the original model system (1). However when the disease remain endemic the disease induced deaths reduce the equilibrium population size from
for the original model system (1). However when the disease remain endemic the disease induced deaths reduce the equilibrium population size from 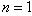 to
to 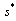 .
.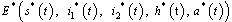 which exists for
which exists for 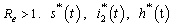 and
and 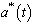 are expressed in terms of
are expressed in terms of 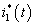 which satisfies the following relations:
which satisfies the following relations: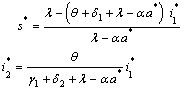
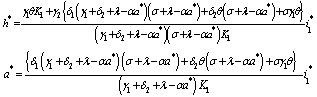 and
and 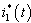 is the solution of the following quadratic polynomial
is the solution of the following quadratic polynomial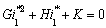
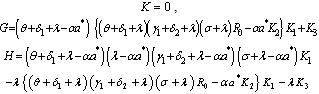 and
and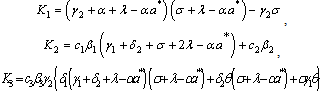 From equation (16) it follows that
From equation (16) it follows that which corresponds to the disease free equilibrium already being discussed or
which corresponds to the disease free equilibrium already being discussed or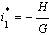 , which gives
, which gives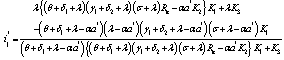
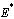 when
when and
and 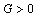 .From this result we state the following theorem which will be proved by using bifurcation diagram and Centre Manifold theorem.Theorem.3.1. The unique endemic equilibrium
.From this result we state the following theorem which will be proved by using bifurcation diagram and Centre Manifold theorem.Theorem.3.1. The unique endemic equilibrium 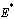 exists if
exists if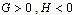 and
and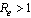 , and is locally stable if
, and is locally stable if 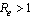 and unstable if
and unstable if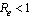 .
.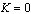 , hence no multiple equilibria. Therefore existence of unique endemic equilibrium which is locally stable for
, hence no multiple equilibria. Therefore existence of unique endemic equilibrium which is locally stable for 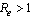 and unstable if
and unstable if 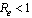 was explored by a forward bifurcation diagram obtained when a graph of proportion of unaware infective ‘
was explored by a forward bifurcation diagram obtained when a graph of proportion of unaware infective ‘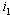 ’against reproduction number ‘
’against reproduction number ‘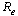 ’ was sketched as shown below:
’ was sketched as shown below:
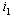 ’ versus effective reproduction number
’ versus effective reproduction number 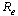
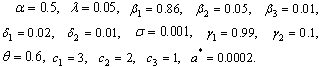 In figure 2 above, the two equilibrium points exchange stabilities depending on the value of
In figure 2 above, the two equilibrium points exchange stabilities depending on the value of 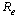 . A transcritical/forward bifurcation in the equilibrium points occur at
. A transcritical/forward bifurcation in the equilibrium points occur at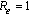 . If
. If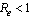 , no biologically meaningful endemic equilibrium solution exists and the disease free equilibrium is the only local attractor. But if
, no biologically meaningful endemic equilibrium solution exists and the disease free equilibrium is the only local attractor. But if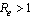 , the endemic equilibrium exists and it is the only local attractor while the disease free equilibrium is a saddle point. Thus there is a forward bifurcation because in the neighbourhood of the bifurcation point, the endemic disease prevalence (proportion of unaware infectives
, the endemic equilibrium exists and it is the only local attractor while the disease free equilibrium is a saddle point. Thus there is a forward bifurcation because in the neighbourhood of the bifurcation point, the endemic disease prevalence (proportion of unaware infectives 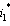 ) is an increasing function of
) is an increasing function of 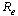 as shown in equation (17).The local asymptotic stability of endemic equilibrium is analyzed by using the Centre Manifold theory[14] and shows that it is stable under certain conditions. The normalised model system (3) shows that it will exhibit a backward bifurcation which occurs at
as shown in equation (17).The local asymptotic stability of endemic equilibrium is analyzed by using the Centre Manifold theory[14] and shows that it is stable under certain conditions. The normalised model system (3) shows that it will exhibit a backward bifurcation which occurs at 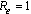 under certain condition otherwise it will exhibit a forward bifurcation at
under certain condition otherwise it will exhibit a forward bifurcation at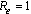 as shown in figure 2 and is locally stable.
as shown in figure 2 and is locally stable.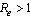 the endemic equilibrium
the endemic equilibrium 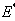 of the normalised model system (3) is globally asymptotically stable.Proof To establish the global stability of endemic equilibrium
of the normalised model system (3) is globally asymptotically stable.Proof To establish the global stability of endemic equilibrium 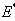 we construct the following positive Lyapunov function V as follows:
we construct the following positive Lyapunov function V as follows: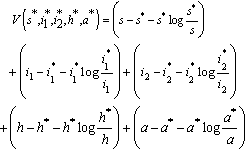
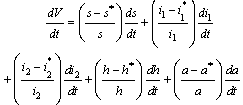
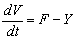
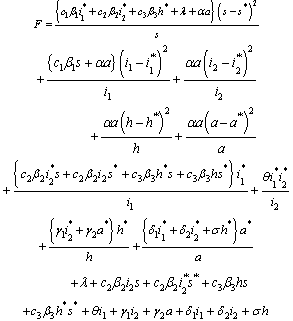 and
and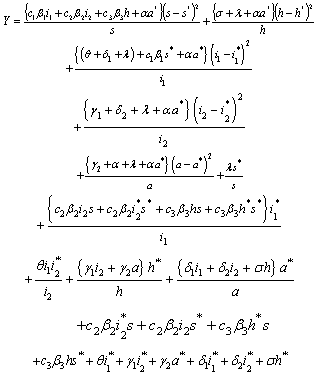 Thus from equation (20), if
Thus from equation (20), if  then
then  will be negative definite, meaning that
will be negative definite, meaning that 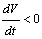 Also it follows that
Also it follows that 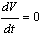 if and only if
if and only if 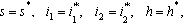
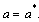 Therefore the largest compact invariant set in
Therefore the largest compact invariant set in 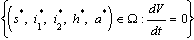 is the singleton
is the singleton 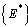 where
where 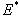 is the endemic equilibrium of the normalised model system (3). By LaSalles’s invariant principle, then it implies that
is the endemic equilibrium of the normalised model system (3). By LaSalles’s invariant principle, then it implies that 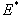 is globally asymptotically stable in
is globally asymptotically stable in 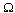 if
if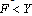 .
.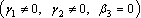
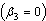 . Thus the infection is transmitted by those infectives who are not aware of their infection and those who are screened only (not using ARV). The basic reproduction number in this case is given by
. Thus the infection is transmitted by those infectives who are not aware of their infection and those who are screened only (not using ARV). The basic reproduction number in this case is given by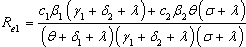 and we note that
and we note that . We also note that
. We also note that  as
as . Therefore we can conclude that the endemicity of the infection is reduced when the treated HIV infectives present a positive attitude towards preventive measures and do not take part in the transmission of the disease.
. Therefore we can conclude that the endemicity of the infection is reduced when the treated HIV infectives present a positive attitude towards preventive measures and do not take part in the transmission of the disease.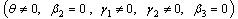
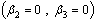 Thus the infection is transmitted only by those infectives who are not aware of their infections. The basic reproduction number in this case is given by
Thus the infection is transmitted only by those infectives who are not aware of their infections. The basic reproduction number in this case is given by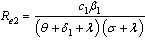 and we note that
and we note that 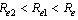 and
and 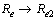 as
as 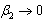 and
and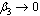 . Therefore we can conclude that the endemicity of the infection is reduced when screened and treated HIV infectives both reflect a positive attitude towards preventive measures and do not take part in the transmission of the disease.
. Therefore we can conclude that the endemicity of the infection is reduced when screened and treated HIV infectives both reflect a positive attitude towards preventive measures and do not take part in the transmission of the disease.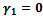 and
and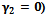
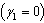 and AIDS population who are not treated
and AIDS population who are not treated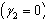 . The normalized model system (3) for this case is reduced to the group of proportion of susceptibles, unaware infectives, screened infectives and AIDS class population. As there is no treatment, i.e.
. The normalized model system (3) for this case is reduced to the group of proportion of susceptibles, unaware infectives, screened infectives and AIDS class population. As there is no treatment, i.e. 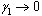 and
and 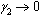 then
then 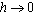 we obtain the basic reproduction number
we obtain the basic reproduction number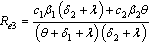 We note that
We note that 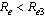 and
and 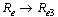 as,
as, 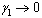 and
and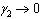 . Therefore we can conclude that the endemicity of the infection in this case increases in the absence of treatment with ARV for the screened infectives and AIDS population.
. Therefore we can conclude that the endemicity of the infection in this case increases in the absence of treatment with ARV for the screened infectives and AIDS population.
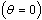 . This Implies that
. This Implies that 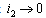 and
and 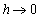 in which case we obtain the basic reproduction number as
in which case we obtain the basic reproduction number as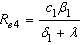 We note that
We note that 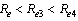 and
and 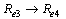 as
as 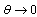 .Therefore we can conclude that the endemicity of the infection in this case increases in the absence of detection of unaware infectives by screening.By analysing the four epidemiological situations discussed above, it may be concluded that in the presence of screening and treatment, if both the screened and treated HIV infectives decide to take preventive measures and do not transmit the infection, the disease will tend to the endemic state if both the screening and treatment rates are small. If the annual screening and treatment rates are very high (say 99% of the initial population), the disease may tend to disease free equilibrium point. However if screened and treated HIV infectives also contribute to the transmission of the disease, then even if both screening and treatment rates are very high, the disease is set up among the population as the system continues towards asymptotically stable endemic equilibrium point. Analysis also shows that the endemicity of the disease is reduced by screening of unaware HIV infectives and treatment of the screened HIV infectives in the population.
.Therefore we can conclude that the endemicity of the infection in this case increases in the absence of detection of unaware infectives by screening.By analysing the four epidemiological situations discussed above, it may be concluded that in the presence of screening and treatment, if both the screened and treated HIV infectives decide to take preventive measures and do not transmit the infection, the disease will tend to the endemic state if both the screening and treatment rates are small. If the annual screening and treatment rates are very high (say 99% of the initial population), the disease may tend to disease free equilibrium point. However if screened and treated HIV infectives also contribute to the transmission of the disease, then even if both screening and treatment rates are very high, the disease is set up among the population as the system continues towards asymptotically stable endemic equilibrium point. Analysis also shows that the endemicity of the disease is reduced by screening of unaware HIV infectives and treatment of the screened HIV infectives in the population.

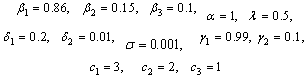
 The equilibrium points of the endemic equilibrium
The equilibrium points of the endemic equilibrium 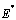 was obtained as
was obtained as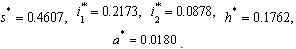 It is seen from these figures that for any starting initial value, the solution curves tend to the equilibrium
It is seen from these figures that for any starting initial value, the solution curves tend to the equilibrium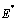 . Therefore we conclude that the normalised model system (3) is globally stable about this endemic equilibrium point
. Therefore we conclude that the normalised model system (3) is globally stable about this endemic equilibrium point 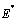 for the estimated parameters above.Figure .4.2 below show the variation of the proportion of total population in all classesIt is seen that the proportion of susceptible population decreases with time and then reaches its equilibrium position. This is due to treatment with ARV. Therefore infection becomes less endemic in the population. Initially proportion of unaware infectives increases but due to the increase in screening and treatment, the rates
for the estimated parameters above.Figure .4.2 below show the variation of the proportion of total population in all classesIt is seen that the proportion of susceptible population decreases with time and then reaches its equilibrium position. This is due to treatment with ARV. Therefore infection becomes less endemic in the population. Initially proportion of unaware infectives increases but due to the increase in screening and treatment, the rates 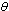 and
and 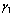 respectively, decreases then reaches its equilibrium position. This ultimately leads to the decrease of the proportion of AIDS infectives.In figures 4.3-4.4, the variation of proportions of susceptible, unaware, screened and treated HIV infective populations and proportion of AIDS patient population for different rates of screening is shown
respectively, decreases then reaches its equilibrium position. This ultimately leads to the decrease of the proportion of AIDS infectives.In figures 4.3-4.4, the variation of proportions of susceptible, unaware, screened and treated HIV infective populations and proportion of AIDS patient population for different rates of screening is shown
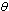

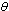

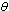

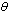

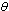

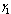 and
and 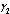

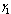 and
and 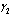

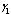 and
and 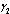

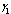 and
and 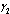

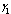 and
and 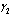
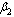 and
and 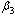 of the screened and treated HIV infectives respectively.
of the screened and treated HIV infectives respectively.
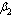 and
and 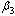 respectively.
respectively.
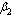 and
and 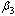 respectively.
respectively.
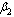 and
and 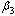 respectively.
respectively.
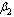 and
and 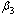 respectively.
respectively.
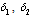 , and
, and 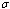

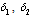 and
and 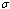

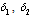 and
and 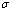

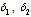 and
and 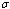

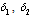 and
and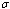 .
.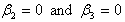 respectively and the proportion of unaware HIV infectives decreases leading to the decrease of proportion of AIDS patients population. From these figures, it is also clear that in the absence of screening of unaware HIV infectives and treatment of screened HIV infectives, the higher proportion of unaware and screened HIV infectives respectively leads to increase of the proportion of AIDS patients population. Thus to keep the transmission of the epidemic under control, the screened and treated HIV infectives individuals should be counselled to either abstain from sexual interaction or use preventive measures like condoms to stop transmitting HIV infection.
respectively and the proportion of unaware HIV infectives decreases leading to the decrease of proportion of AIDS patients population. From these figures, it is also clear that in the absence of screening of unaware HIV infectives and treatment of screened HIV infectives, the higher proportion of unaware and screened HIV infectives respectively leads to increase of the proportion of AIDS patients population. Thus to keep the transmission of the epidemic under control, the screened and treated HIV infectives individuals should be counselled to either abstain from sexual interaction or use preventive measures like condoms to stop transmitting HIV infection.
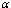

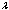
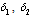 and
and 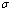 of unaware, screened and treated infectives respectively.It is seen that as the movement rates from infective classes increases, proportions of all infective classes populations decreases (Figures 4.8 (ii), (iii) and (iv)) which in turn increases the proportion of AIDS patients population (Figure.4.9) and also increases the proportion of susceptible population (Figure 4.8 (i)).Figures 4.10 show the variation of proportion of AIDS patients population for different values of disease induced death rate
of unaware, screened and treated infectives respectively.It is seen that as the movement rates from infective classes increases, proportions of all infective classes populations decreases (Figures 4.8 (ii), (iii) and (iv)) which in turn increases the proportion of AIDS patients population (Figure.4.9) and also increases the proportion of susceptible population (Figure 4.8 (i)).Figures 4.10 show the variation of proportion of AIDS patients population for different values of disease induced death rate 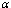 and recruitment rate
and recruitment rate 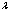 of susceptibles respectively.It is observed from the figures that as
of susceptibles respectively.It is observed from the figures that as 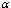 increases the proportion of AIDS patients population decreases and it is also observed that as the recruitment rate increases, the proportion of AIDS patient population increases.
increases the proportion of AIDS patients population decreases and it is also observed that as the recruitment rate increases, the proportion of AIDS patient population increases. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML