Bhaskar Srivastava
Department of Mathematics and Astronomy, Lucknow University, Lucknow, India
Correspondence to: Bhaskar Srivastava , Department of Mathematics and Astronomy, Lucknow University, Lucknow, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We define bilateral series for two sets of new mock theta functions-- one given by Andrews and the other by Bringmann et al. Not only the bilateral form of the mock theta functions in the two sets are equivalent they further come out to be equivalent to the bilateral form of the eighth order mock theta functions of Gordon and McIntosh. These bilateral series are expressed as a q-hypergeometric 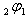 series and then represented by continued fractions. We extend the definition of the bilateral mock theta functions and show they are
series and then represented by continued fractions. We extend the definition of the bilateral mock theta functions and show they are 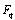 -functions and relations are then defined.
-functions and relations are then defined.
Keywords:
Mock Theta Functions, Bilateral Series, Continued Fractions
1. Introduction
In his last letter to G.H. Hardy[11], S. Ramanujan listed seventeen mock theta functions of order three, five, five and seven. According to Ramanujan a mock theta function is a function 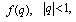 satisfying the following two conditions:(0) For every root of unity
satisfying the following two conditions:(0) For every root of unity 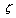 , there is a
, there is a 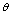 -function
-function 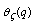 such that the difference
such that the difference 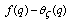 is bounded as
is bounded as 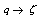 radially. (1) There is no single
radially. (1) There is no single 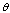 -function which works for all
-function which works for all 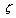 i.e., for every
i.e., for every 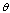 -function
-function 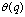 there is some root of unity
there is some root of unity 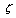 for which
for which 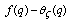 is unbounded as
is unbounded as 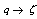 radially.G.N. Watson[17] found three more mock theta functions of order three. In his “Lost” Notebook Ramanujan gave six more mock theta functions which were called by G.E. Andrews and D. Hickerson[5] of order six and four mock theta functions which were called by Choi[6] of order ten. B. Gordon and R.J. McIntosh[8] generated eight mock theta functions and called them of order eight, but four of them were later found of lower order. Hikami[9] found one more mock theta function of order two.Recently Andrews[2] in his paper generated some new mock theta functions and found four of them interesting. Bringmann, Hikami and Lovejoy developed two more mock theta functions. We in[12-14] have made a comprehensive study of these mock theta functions. After studying these mock theta functions in[12-14] I started considering their bilateral form. The study became interesting as in their bilateral form the mock theta functions The four mock theta functions of Andrews [2]:
radially.G.N. Watson[17] found three more mock theta functions of order three. In his “Lost” Notebook Ramanujan gave six more mock theta functions which were called by G.E. Andrews and D. Hickerson[5] of order six and four mock theta functions which were called by Choi[6] of order ten. B. Gordon and R.J. McIntosh[8] generated eight mock theta functions and called them of order eight, but four of them were later found of lower order. Hikami[9] found one more mock theta function of order two.Recently Andrews[2] in his paper generated some new mock theta functions and found four of them interesting. Bringmann, Hikami and Lovejoy developed two more mock theta functions. We in[12-14] have made a comprehensive study of these mock theta functions. After studying these mock theta functions in[12-14] I started considering their bilateral form. The study became interesting as in their bilateral form the mock theta functions The four mock theta functions of Andrews [2]: 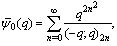 | (1.1) |
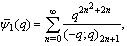 | (1.2) |
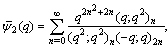 | (1.3) |
and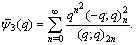 | (1.4) |
Andrews called 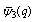 as a companion to the third order mock theta function of Ramanujan
as a companion to the third order mock theta function of Ramanujan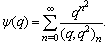 The two mock theta functions of Bringmann, Hikami and Lovejoy [10]:
The two mock theta functions of Bringmann, Hikami and Lovejoy [10]: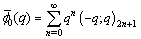 | (1.5) |
and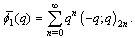 | (1.6) |
We now write the mock theta function as basic bilateral series, and following Watson, call them ’Complete’. 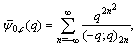 | (1.7) |
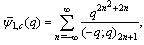 | (1.8) |
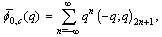 | (1.9) |
and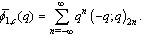 | (1.10) |
The scheme of the paper is as follows:In section 3, we give an expansion for these functions using Slater’s expansion formula[7] and show their relationship with other bilateral mock theta functions.In section 4 and section 5, we express these ‘complete’ mock theta functions as 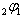 series.In section 6, we represent these ‘complete’ mock theta functions as continued fractions.In section 7, we give alternative definitions, using Bailey’s bilateral transformation[7]. In section 8, relationship between two sets of bilateral mock theta functions is shown.In section 9 and 10, we define extended form for the ‘complete’ mock theta functions and show that they are
series.In section 6, we represent these ‘complete’ mock theta functions as continued fractions.In section 7, we give alternative definitions, using Bailey’s bilateral transformation[7]. In section 8, relationship between two sets of bilateral mock theta functions is shown.In section 9 and 10, we define extended form for the ‘complete’ mock theta functions and show that they are 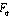 - functions and certain relationship between these functions.
- functions and certain relationship between these functions.
2. Basic Standard Results
We shall use the following usual basic hypergeometric notations: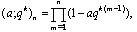 qk < 1, n, non negative integer
qk < 1, n, non negative integer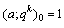 ,
,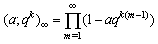
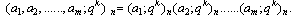
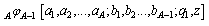
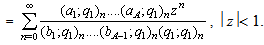 A generalized basic bilateral series is defined as
A generalized basic bilateral series is defined as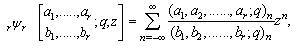 where
where 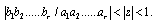
3. Relations between Bilateral Mock Theta Functions
Taking r = 2 in the following expansion of Slater [7, (5.4.3), p. 129]: 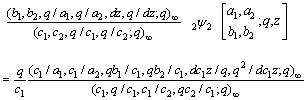
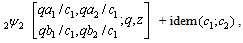 | (3.1) |
where 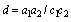 ,
, 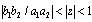 , and idem
, and idem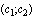 after the expression means that the preceding expression is repeated with
after the expression means that the preceding expression is repeated with 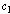 and
and 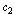 interchanged. We now give expansions for these bilateral mock theta functions.(i) Letting
interchanged. We now give expansions for these bilateral mock theta functions.(i) Letting 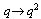 ,
,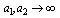 and taking
and taking 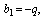
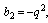
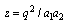 in (3.1), we have
in (3.1), we have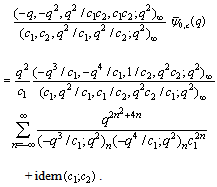 | (3.2) |
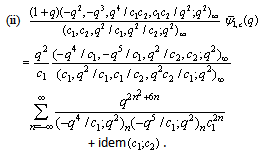 | (3.3) |
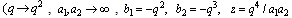 , in (3.1))
, in (3.1))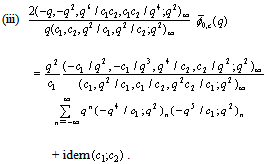 | (3.4) |
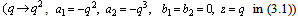
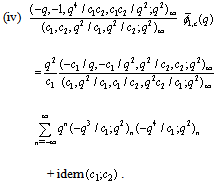 | (3.5) |
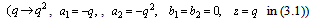 Relations between bilateral mock theta functions Special CasesTake
Relations between bilateral mock theta functions Special CasesTake 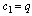 in (3.2) :
in (3.2) :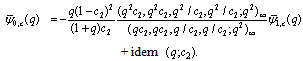 | (3.6) |
Take 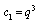 in (3.3):
in (3.3):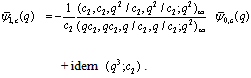 | (3.7) |
Take 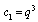 in (3.4):
in (3.4):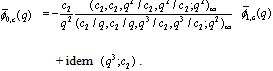 | (3.8) |
Take 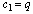 in (3.5):
in (3.5):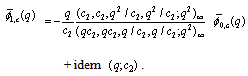 | (3.9) |
4. Expansion of Bilateral Mock Theta Functions 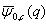 and
and 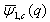 as
as 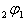 Series
Series
In (3.1) we take 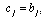
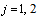 to get [7, (5.4.5), p. 130]
to get [7, (5.4.5), p. 130]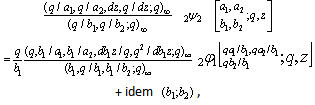 | (4.1) |
where 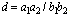 .We will now specialize the paramaeter in (4.1) to get expansions of bilateral mock theta functions as q- hypergeometric series.(i) Letting
.We will now specialize the paramaeter in (4.1) to get expansions of bilateral mock theta functions as q- hypergeometric series.(i) Letting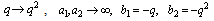 and
and 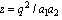 in (4.1), to get
in (4.1), to get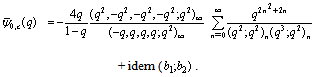 | (4.2) |
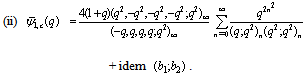 | (4.3) |
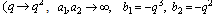 and
and 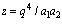 in (4.1))
in (4.1))
5. Expansions of Bilateral Mock Theta Functions 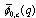 and
and 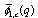 as
as 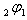 Series
Series
For getting the expansion of a bilateral series as a 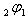 series, we shall use the following expansion formula, which is obtained by putting
series, we shall use the following expansion formula, which is obtained by putting 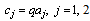 in Slater’s expansion formula (3.1) [7, (5.4.4), p. 130]:
in Slater’s expansion formula (3.1) [7, (5.4.4), p. 130]: 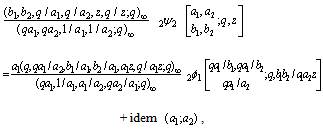 | (5.1) |
(i) Letting 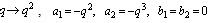 and
and 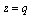 in (5.1), we have
in (5.1), we have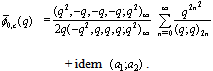 | (5.2) |
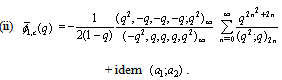 | (5.3) |
(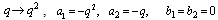 and
and 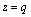 in (5.1))
in (5.1))
6. Bilateral or ‘Complete’ Mock Theta Functions as Continued Fractions
We first write the bilateral 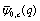 as the sum of two
as the sum of two 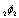 basic hypergeometric series and then use the continued fraction [1,(3.79) p 82]:
basic hypergeometric series and then use the continued fraction [1,(3.79) p 82]: 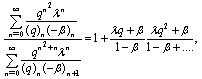 | (6.1) |
to represent 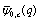 as a continued fraction.(i) Now (4.2) gives
as a continued fraction.(i) Now (4.2) gives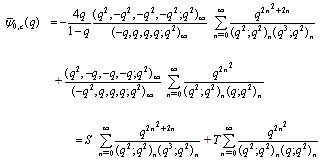 | (6.2) |
where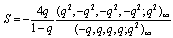 and
and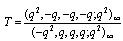 Dividing the expressions on both sides of (6.2) by the first summation on the right side of (6.2), we have
Dividing the expressions on both sides of (6.2) by the first summation on the right side of (6.2), we have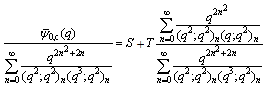 | (6.3) |
Letting 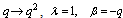 in (6.1), and then putting it in the quotient of the summation on the right side of (6.3) to have(ii) Similarly by (4.3), we have
in (6.1), and then putting it in the quotient of the summation on the right side of (6.3) to have(ii) Similarly by (4.3), we have 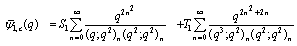 where
where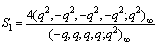 and
and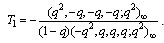 .Hence we have
.Hence we have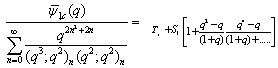 | (6.5) |
(iii) For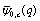 we will have the same continued fraction by (8.2).(iv) For
we will have the same continued fraction by (8.2).(iv) For 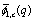 we will have the same continued fraction by (8.4).
we will have the same continued fraction by (8.4).
7. Alternative Definitions for ‘Complete’ Mock Theta Functions
We shall use the following bilateral transformation of Bailey [7, 5.20(ii), p 137] to get alternative definition : 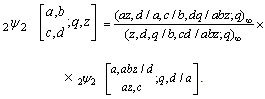 | (7.1) |
and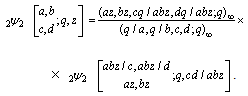 | (7.2) |
(i) Let 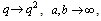 and take
and take 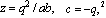
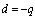 , in (7.1) and (7.2), respectively, to get
, in (7.1) and (7.2), respectively, to get 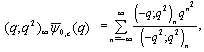 | (7.3) |
and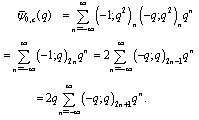 | (7.4) |
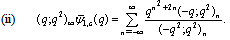 | (7.5) |
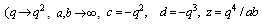 in (7.1))
in (7.1))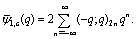 | (7.6) |
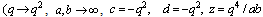 in 7.2))
in 7.2))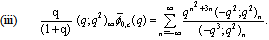 | (7.7) |
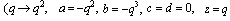 in (7.1))
in (7.1))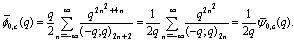 | (7.8) |
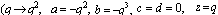 in (7.2))
in (7.2))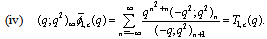 | (7.9) |
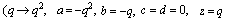 in (7.1))
in (7.1))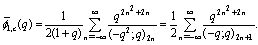 | (7.10) |
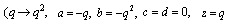 in (7.2))
in (7.2))
8. Relationship between Bilateral Mock Theta Functions
From these alternative definition it is interesting to note that bilateral mock theta functions developed by Andrews can be expressed as bilateral mock theta functions developed by Bringmann et al.From (7.3)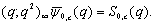 | (8.1) |
From (7.4)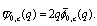 | (8.2) |
From (7.5)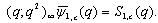 | (8.3) |
From (7.6)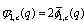 | (8.4) |
From (7.7)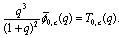 | (8.5) |
From (7.8)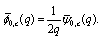 | (8.6) |
From (7.9)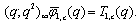 | (8.7) |
From (7.10)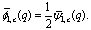 | (8.8) |
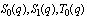 and
and 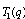 are eighth order mock theta functions given by Gordon and McIntosh [8].
are eighth order mock theta functions given by Gordon and McIntosh [8].
9. Extended Form for Bilateral ‘Complete’ Mock Theta Functions
We define the extended ‘Complete’ mock theta functions: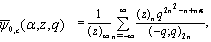 | (9.1) |
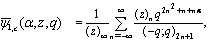 | (9.2) |
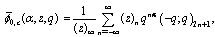 | (9.3) |
and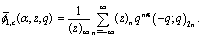 | (9.4) |
For 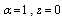 these extended functions reduce to the bilateral mock theta functions. We show they are
these extended functions reduce to the bilateral mock theta functions. We show they are 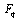 -functions. Before we prove they are
-functions. Before we prove they are 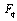 -functions, we define a
-functions, we define a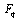 -function.Truesdell[15] calls the functions which satisfy the functional equation
-function.Truesdell[15] calls the functions which satisfy the functional equation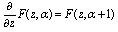 ,F-functions. The q-analogue is that the functions which satisfy the functional equation
,F-functions. The q-analogue is that the functions which satisfy the functional equation 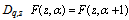 ,where
,where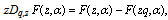 are called
are called 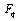 -Functions.By definition
-Functions.By definition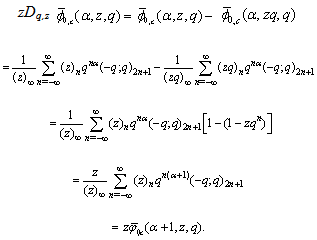 Hence
Hence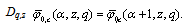 Thus
Thus 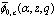 is a
is a 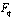 -function. Similarly, all other functions listed in section 9 are
-function. Similarly, all other functions listed in section 9 are 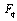 - functions.
- functions.
10. Relations between Extended Functions
Now we give a relationship between these generalized mock theta functions.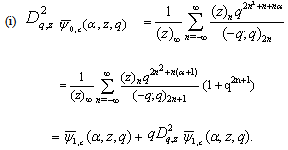
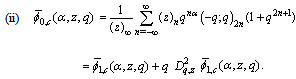
11. Conclusions
The study of basic bilateral mock theta functions is interesting as it gives alternative forms and close relationship among the mock theta functions. We have expressed them as 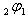 series and represented them as continued fractions. The same method can be applied for other classical mock theta functionsI have considered these mock theta functions (1.1)--(1.6) in detail finding their properties and expansions etc [12], [13] and [14].
series and represented them as continued fractions. The same method can be applied for other classical mock theta functionsI have considered these mock theta functions (1.1)--(1.6) in detail finding their properties and expansions etc [12], [13] and [14].
References
| [1] | R.P. Agarwal, Resonance of Ramanujan’s Mathematics III, New Age International (P) Ltd. New Delhi (1996). |
| [2] | G. E. Andrews, q-orthogonal polynomials, Rogers- Ramanujan identities, and mock theta functions, preprint. |
| [3] | G. E. Andrews, q-Series: Their Development.,CBMS regional conference lecture series 66 (1986), Amer Math. Soc. Providence. |
| [4] | G. E. Andrews, Parity in partition identities, Ramanujan Journal (to appear). |
| [5] | G. E. Andrews, D. Hickerson, Ramanujan’s “Lost” Notebook VII: The sixth order mock theta functions, Adv. in Math. 89 (1991), 60-105. |
| [6] | Youn-Seo Choi, Tenth order mock theta functions in Ramanujan’s ‘Lost’ Notebook, Invent. Math. 136 (1999), 497-569. |
| [7] | G. Gasper and M. Rahman, Basic Hypergeometric Series, Cambridge University Press, Cambridge (1990). |
| [8] | B.Gordon and R.J. McIntosh, Some eighth order mock theta functions, J. London Math. Soc. 62(2) (2000), 321-335 |
| [9] | K. Hikami, Transformation formula of the “2nd” order mock theta function, Lett. Math. Phys., 75(1) (2006), 93-98. |
| [10] | E. Mortess, On three third order mock theta functions and Hecke-type double sums (preprint). |
| [11] | S. Ramanujan, Collected Papers, Cambridge University Press, 1972, reprinted Chelsea, New York, 1962. |
| [12] | Bhaskar Srivastava, A generalization and study of four new mock theta functions (Communicated). |
| [13] | Bhaskar Srivastava, Some new mock theta functions, accepted in Math. Sci. Research J. |
| [14] | Bhaskar Srivastava, Partial new mock theta functions (Communicated). |
| [15] | C Truesdell, An essay toward a unified theory of special functions, Princeton University Press, Princeton, (1948). |
| [16] | G.N. Watson, The final problem: An account of the mock theta functions, J. London Math. Soc. 11 (1936), 55-80. |
| [17] | G.N. Watson, The Mock Theta FunctionsII, Proc. London Math. Soc. (2) 42 (1937), 272- 304. |

 series and then represented by continued fractions. We extend the definition of the bilateral mock theta functions and show they are
series and then represented by continued fractions. We extend the definition of the bilateral mock theta functions and show they are 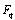 -functions and relations are then defined.
-functions and relations are then defined.
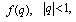 satisfying the following two conditions:(0) For every root of unity
satisfying the following two conditions:(0) For every root of unity 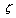 , there is a
, there is a 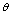 -function
-function 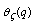 such that the difference
such that the difference 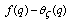 is bounded as
is bounded as 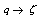 radially. (1) There is no single
radially. (1) There is no single 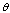 -function which works for all
-function which works for all 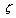 i.e., for every
i.e., for every 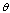 -function
-function 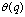 there is some root of unity
there is some root of unity 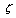 for which
for which 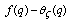 is unbounded as
is unbounded as 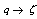 radially.G.N. Watson[17] found three more mock theta functions of order three. In his “Lost” Notebook Ramanujan gave six more mock theta functions which were called by G.E. Andrews and D. Hickerson[5] of order six and four mock theta functions which were called by Choi[6] of order ten. B. Gordon and R.J. McIntosh[8] generated eight mock theta functions and called them of order eight, but four of them were later found of lower order. Hikami[9] found one more mock theta function of order two.Recently Andrews[2] in his paper generated some new mock theta functions and found four of them interesting. Bringmann, Hikami and Lovejoy developed two more mock theta functions. We in[12-14] have made a comprehensive study of these mock theta functions. After studying these mock theta functions in[12-14] I started considering their bilateral form. The study became interesting as in their bilateral form the mock theta functions The four mock theta functions of Andrews [2]:
radially.G.N. Watson[17] found three more mock theta functions of order three. In his “Lost” Notebook Ramanujan gave six more mock theta functions which were called by G.E. Andrews and D. Hickerson[5] of order six and four mock theta functions which were called by Choi[6] of order ten. B. Gordon and R.J. McIntosh[8] generated eight mock theta functions and called them of order eight, but four of them were later found of lower order. Hikami[9] found one more mock theta function of order two.Recently Andrews[2] in his paper generated some new mock theta functions and found four of them interesting. Bringmann, Hikami and Lovejoy developed two more mock theta functions. We in[12-14] have made a comprehensive study of these mock theta functions. After studying these mock theta functions in[12-14] I started considering their bilateral form. The study became interesting as in their bilateral form the mock theta functions The four mock theta functions of Andrews [2]: 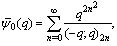
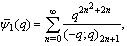
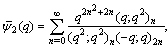
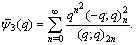
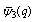 as a companion to the third order mock theta function of Ramanujan
as a companion to the third order mock theta function of Ramanujan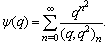 The two mock theta functions of Bringmann, Hikami and Lovejoy [10]:
The two mock theta functions of Bringmann, Hikami and Lovejoy [10]: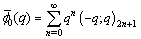
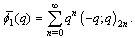
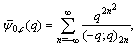
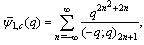
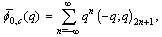
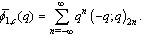
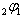 series.In section 6, we represent these ‘complete’ mock theta functions as continued fractions.In section 7, we give alternative definitions, using Bailey’s bilateral transformation[7]. In section 8, relationship between two sets of bilateral mock theta functions is shown.In section 9 and 10, we define extended form for the ‘complete’ mock theta functions and show that they are
series.In section 6, we represent these ‘complete’ mock theta functions as continued fractions.In section 7, we give alternative definitions, using Bailey’s bilateral transformation[7]. In section 8, relationship between two sets of bilateral mock theta functions is shown.In section 9 and 10, we define extended form for the ‘complete’ mock theta functions and show that they are 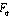 - functions and certain relationship between these functions.
- functions and certain relationship between these functions.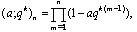 qk < 1, n, non negative integer
qk < 1, n, non negative integer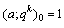 ,
,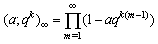
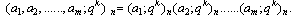
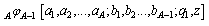
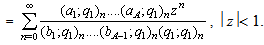 A generalized basic bilateral series is defined as
A generalized basic bilateral series is defined as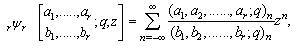 where
where 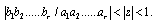
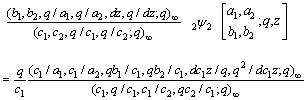
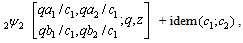
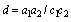 ,
, 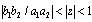 , and idem
, and idem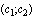 after the expression means that the preceding expression is repeated with
after the expression means that the preceding expression is repeated with 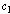 and
and 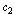 interchanged. We now give expansions for these bilateral mock theta functions.(i) Letting
interchanged. We now give expansions for these bilateral mock theta functions.(i) Letting 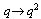 ,
,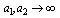 and taking
and taking 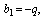
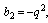
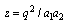 in (3.1), we have
in (3.1), we have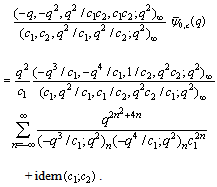
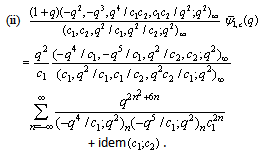
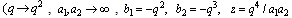 , in (3.1))
, in (3.1))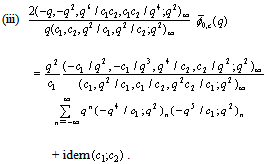
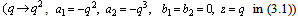
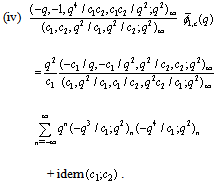
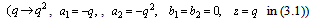 Relations between bilateral mock theta functions Special CasesTake
Relations between bilateral mock theta functions Special CasesTake 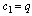 in (3.2) :
in (3.2) :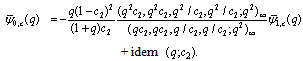
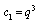 in (3.3):
in (3.3):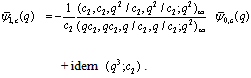
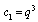 in (3.4):
in (3.4):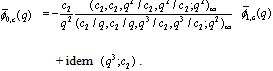
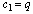 in (3.5):
in (3.5):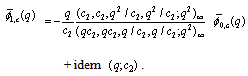
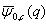 and
and 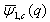 as
as 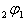 Series
Series 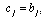
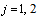 to get [7, (5.4.5), p. 130]
to get [7, (5.4.5), p. 130]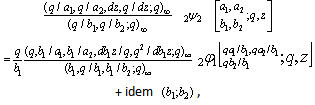
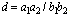 .We will now specialize the paramaeter in (4.1) to get expansions of bilateral mock theta functions as q- hypergeometric series.(i) Letting
.We will now specialize the paramaeter in (4.1) to get expansions of bilateral mock theta functions as q- hypergeometric series.(i) Letting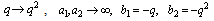 and
and 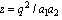 in (4.1), to get
in (4.1), to get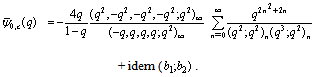
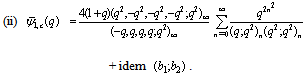
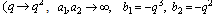 and
and 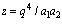 in (4.1))
in (4.1))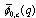 and
and 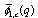 as
as 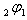 Series
Series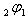 series, we shall use the following expansion formula, which is obtained by putting
series, we shall use the following expansion formula, which is obtained by putting 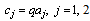 in Slater’s expansion formula (3.1) [7, (5.4.4), p. 130]:
in Slater’s expansion formula (3.1) [7, (5.4.4), p. 130]: 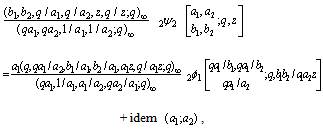
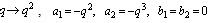 and
and 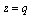 in (5.1), we have
in (5.1), we have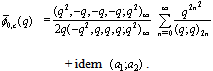
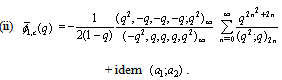
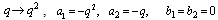 and
and 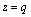 in (5.1))
in (5.1))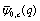 as the sum of two
as the sum of two 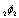 basic hypergeometric series and then use the continued fraction [1,(3.79) p 82]:
basic hypergeometric series and then use the continued fraction [1,(3.79) p 82]: 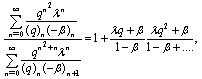
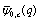 as a continued fraction.(i) Now (4.2) gives
as a continued fraction.(i) Now (4.2) gives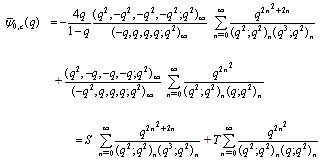
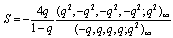 and
and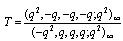 Dividing the expressions on both sides of (6.2) by the first summation on the right side of (6.2), we have
Dividing the expressions on both sides of (6.2) by the first summation on the right side of (6.2), we have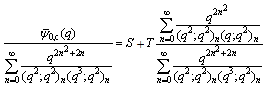
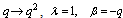 in (6.1), and then putting it in the quotient of the summation on the right side of (6.3) to have(ii) Similarly by (4.3), we have
in (6.1), and then putting it in the quotient of the summation on the right side of (6.3) to have(ii) Similarly by (4.3), we have 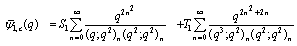 where
where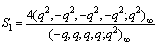 and
and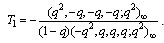 .Hence we have
.Hence we have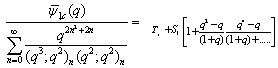
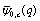 we will have the same continued fraction by (8.2).(iv) For
we will have the same continued fraction by (8.2).(iv) For 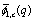 we will have the same continued fraction by (8.4).
we will have the same continued fraction by (8.4).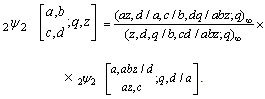
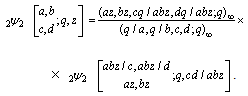
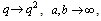 and take
and take 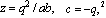
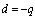 , in (7.1) and (7.2), respectively, to get
, in (7.1) and (7.2), respectively, to get 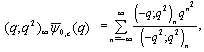
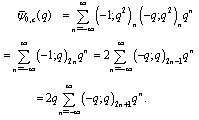
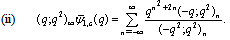
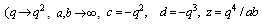 in (7.1))
in (7.1))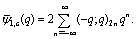
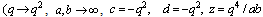 in 7.2))
in 7.2))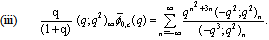
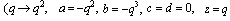 in (7.1))
in (7.1))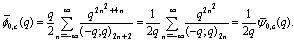
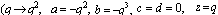 in (7.2))
in (7.2))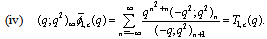
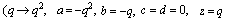 in (7.1))
in (7.1))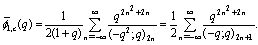
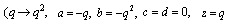 in (7.2))
in (7.2))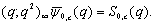
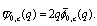
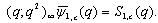
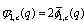
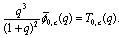
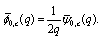
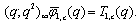
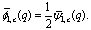
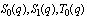 and
and 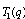 are eighth order mock theta functions given by Gordon and McIntosh [8].
are eighth order mock theta functions given by Gordon and McIntosh [8].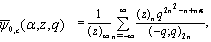
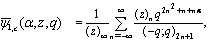
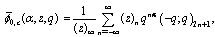
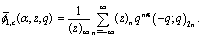
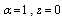 these extended functions reduce to the bilateral mock theta functions. We show they are
these extended functions reduce to the bilateral mock theta functions. We show they are 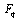 -functions. Before we prove they are
-functions. Before we prove they are 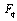 -functions, we define a
-functions, we define a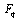 -function.Truesdell[15] calls the functions which satisfy the functional equation
-function.Truesdell[15] calls the functions which satisfy the functional equation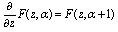 ,F-functions. The q-analogue is that the functions which satisfy the functional equation
,F-functions. The q-analogue is that the functions which satisfy the functional equation 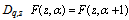 ,where
,where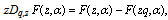 are called
are called 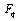 -Functions.By definition
-Functions.By definition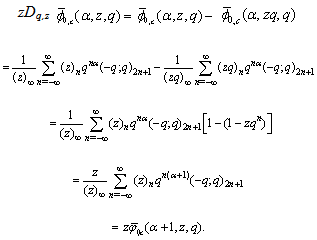 Hence
Hence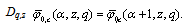 Thus
Thus 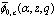 is a
is a 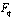 -function. Similarly, all other functions listed in section 9 are
-function. Similarly, all other functions listed in section 9 are 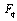 - functions.
- functions.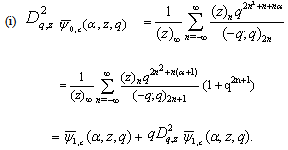
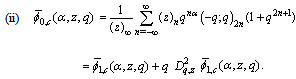
 series and represented them as continued fractions. The same method can be applied for other classical mock theta functionsI have considered these mock theta functions (1.1)--(1.6) in detail finding their properties and expansions etc [12], [13] and [14].
series and represented them as continued fractions. The same method can be applied for other classical mock theta functionsI have considered these mock theta functions (1.1)--(1.6) in detail finding their properties and expansions etc [12], [13] and [14]. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML