-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2012; 2(3): 49-56
doi: 10.5923/j.ajms.20120203.07
Superstatistics and Lifetime
V. V. Ryazanov
Institute for Nuclear Research Ukrainian Academy of Science, 47, Nauki Avenue, Kiev, 03068, Ukraine
Correspondence to: V. V. Ryazanov , Institute for Nuclear Research Ukrainian Academy of Science, 47, Nauki Avenue, Kiev, 03068, Ukraine.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
To describe the nonequilibrium states of a system we introduce a new thermodynamic parameter - the lifetime of a system. The statistical distributions which can be obtained out of the mesoscopic description characterizing the behaviour of a system by specifying the stochastic processes are written. Superstatistics, introduced as fluctuating quantities of intensive thermodynamical parameters, are obtained from statistical distribution with lifetime (random time to system degeneracy) as thermodynamical parameter (and also generalization of superstatistics). Necessary for this realization condition with expression for average lifetime of equilibrium statistical system obtained from stochastical storage model is consist. The obtained distribution passes in Gibbs or in superstatistics distribution depending on a measure of dissipativity in the system.
Keywords: Lifetime, Superstatistics, Statistical Distributions
Article Outline
1. Introduction
- In[1] the generalization of Boltzmann factor exp{-β0E} was introduced in the following form:
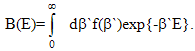 | (1) |
2. System Lifetime and Lifetime Distribution
- Characterizing the nonequilibrium state by means of an additional parameter related to the deviation of a system from the equilibrium (field of gravity, electric field for dielectrics etc) was used in[6]. In the present paper we suggest a new choice of such an additional parameter as the lifetime of a physical system which is defined as a first-passage time till the random process y(t) describing the behaviour of the macroscopic parameter of a system (energy, for example) reaches its zero value. The lifetime is thus a random process which is slave (in terms of the definitions of the theory of random processes[7]) with respect to the master process y(t),
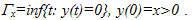 | (2) |
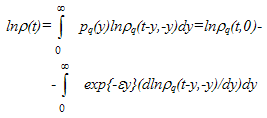 | (3) |
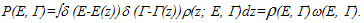 | (4) |
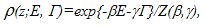 | (5) |
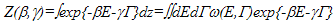 | (6) |
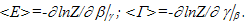 | (7) |
3. Distribution for Nondisturbanced Lifetime
- If γ=0 and β=β0=(kBTeq)-1, where kB is the Boltzmann constant, Teq is the equilibrium temperature, then the expressions (5-6) yield the equilibrium Gibbs distribution. One can thus consider (5-6) as a generalization of the Gibbs statistics to cover the nonequilibrium situation. Such physical phenomena as the metastability, phase transitions, stationary nonequilibrium states are known to violate the equiprobability of the phase space points. The value γ can be regarded as a measure of the deviation from the equiprobability hypothesis. Of coarse, the thermodynamic description itself is supposed to be already coarse-grained. To get the explicit form of the Γ distribution we shall use the general results of the mathematical theory of phase coarsening of the complex systems[16], which imply the following distribution of the lifetime for coarsened random process:
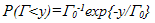 | (8) |
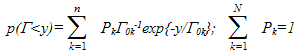 | (9) |
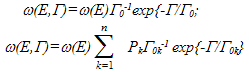 | (10) |
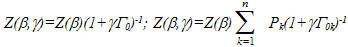 | (11) |
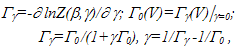 | (12) |
4. Superstatistics from Distribution of the Kind (5)
- In the distribution (5) containing lifetime, as thermodynamic parameter, probability for and Γ is equal
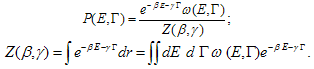 | (13) |
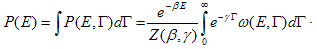 | (14) |
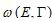 is meaningful to joint probability for E and Γ, treated as stationary distribution of this process. We shall write down
is meaningful to joint probability for E and Γ, treated as stationary distribution of this process. We shall write down 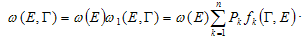 | (15) |
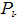 is the probability of that the system will be in k-th a class of ergodic states,
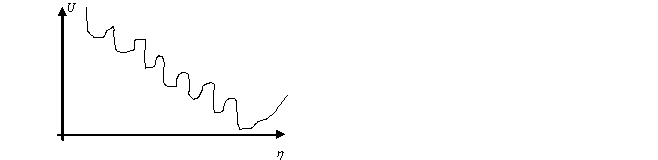
is the probability of that the system will be in k-th a class of ergodic states, 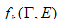 is density of distribution of lifetime Γ in this class of ergodic states (generally fk depends from E). As physical example of such situation (characteristic for metals, glasses) one can mention the potential of many complex systems of a kind, for example, Figure 1. Such situation is considered in[21]. Minima of potential correspond to the metastable phases, disproportionate structures, etc. Essential object of research of statistical physics recently became complex nonergodic systems: the spin and structural glasses, disorder geteropolimery, the granular media, transport currents, etc.[22]. The basic feature of such systems will be, that their phase space is divided into isolated areas, each of which corresponds to a metastable thermodynamic state, and the number of these areas exponential exceeds full number (quasi)particles[23]. The quasithermodynamical theory of structural transformations of alloy Pd-Ta-H, based on this model, is constructed in[24]. Expression (15) to the description of such systems is applicable.
is density of distribution of lifetime Γ in this class of ergodic states (generally fk depends from E). As physical example of such situation (characteristic for metals, glasses) one can mention the potential of many complex systems of a kind, for example, Figure 1. Such situation is considered in[21]. Minima of potential correspond to the metastable phases, disproportionate structures, etc. Essential object of research of statistical physics recently became complex nonergodic systems: the spin and structural glasses, disorder geteropolimery, the granular media, transport currents, etc.[22]. The basic feature of such systems will be, that their phase space is divided into isolated areas, each of which corresponds to a metastable thermodynamic state, and the number of these areas exponential exceeds full number (quasi)particles[23]. The quasithermodynamical theory of structural transformations of alloy Pd-Ta-H, based on this model, is constructed in[24]. Expression (15) to the description of such systems is applicable.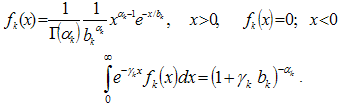 | (16) |
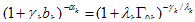 ; Γ0k is equal to average lifetime in k-th a class of metastable states without disturbance, that is, in equilibrium. For average lifetime of the system in dynamical equilibrium state in work[25] by means of stochastic models of storage it is obtained
; Γ0k is equal to average lifetime in k-th a class of metastable states without disturbance, that is, in equilibrium. For average lifetime of the system in dynamical equilibrium state in work[25] by means of stochastic models of storage it is obtained 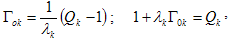 | (17) |
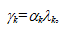 | (18) |
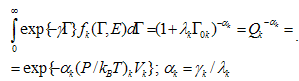 | (19) |
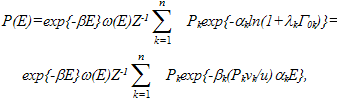 | (20) |
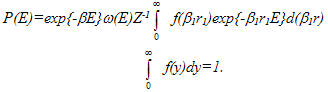 | (21) |
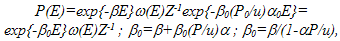 where β is the Lagrange parameter; value β0=1/kBT0 corresponds to average return temperature of full system; kBT0 characterizes the conveniently averaged energy; r0=(P0/u)α0 = (P/u)α for full system; lnQ=β0PV; β=β0(1-αP/u)=β0(1-r0). Substituting this value β in (21) and replacing β1 by β01=1/kBTk=1/kBT1(r,t), the fluktuating value of temperature, we get:
where β is the Lagrange parameter; value β0=1/kBT0 corresponds to average return temperature of full system; kBT0 characterizes the conveniently averaged energy; r0=(P0/u)α0 = (P/u)α for full system; lnQ=β0PV; β=β0(1-αP/u)=β0(1-r0). Substituting this value β in (21) and replacing β1 by β01=1/kBTk=1/kBT1(r,t), the fluktuating value of temperature, we get: 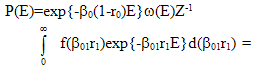 | (22) |
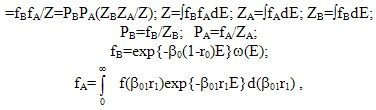 where fA and PA corresponds to the type-A superstatistics from[26]. For f(β01r1)=δ(β01r1-β0r0) we obtain from (22) the ordinary Boltzmann factor. Equality β01r1=β0r0 it is possible at β01≈β0, αkVkPk≈αVP. As in[1], we can write down P(E)= exp{-β0(1-r0)E}ω(E)Z-1exp{-β0r0E}[1+σ2E2/2+O(σ3E3)]=exp{-β0E}ω(E)Z-1[1+(q`-1)(β0r0)2E2+g(q`)(β0r0)3E3+…], where (q`-1)(β0r0)2=σ2, q`=<(β0r0)2>/<(β0r0)>2; (q`-1)1/2=σ/(β0r0); σ2=<(β01r1)2>-(β0r0)2; value β from[1] replace by β01r1, the fluktuating intensive parameter is equal β01r1 instead of β as in[1]; β0r0=<β01r1>= ∫β01r1f(β01r1)d(β01r1), function g(q`) depends on the superstatistics chosen. For f=fG from (16), (23), q`=q=qTs[2,3]. For others f: q`=qBC[1]. For any distribution f(β01r1) with average β0r0=<β01r1> and variance σ2 we can write P(E)∼exp{-β0(1-r0)E}
where fA and PA corresponds to the type-A superstatistics from[26]. For f(β01r1)=δ(β01r1-β0r0) we obtain from (22) the ordinary Boltzmann factor. Equality β01r1=β0r0 it is possible at β01≈β0, αkVkPk≈αVP. As in[1], we can write down P(E)= exp{-β0(1-r0)E}ω(E)Z-1exp{-β0r0E}[1+σ2E2/2+O(σ3E3)]=exp{-β0E}ω(E)Z-1[1+(q`-1)(β0r0)2E2+g(q`)(β0r0)3E3+…], where (q`-1)(β0r0)2=σ2, q`=<(β0r0)2>/<(β0r0)>2; (q`-1)1/2=σ/(β0r0); σ2=<(β01r1)2>-(β0r0)2; value β from[1] replace by β01r1, the fluktuating intensive parameter is equal β01r1 instead of β as in[1]; β0r0=<β01r1>= ∫β01r1f(β01r1)d(β01r1), function g(q`) depends on the superstatistics chosen. For f=fG from (16), (23), q`=q=qTs[2,3]. For others f: q`=qBC[1]. For any distribution f(β01r1) with average β0r0=<β01r1> and variance σ2 we can write P(E)∼exp{-β0(1-r0)E}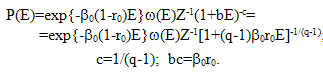 | (23) |
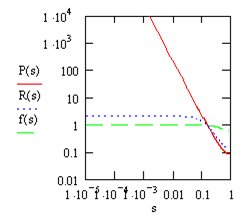
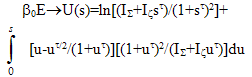 from[30] for a case fluktuated formations of avalanches with an integer exponent of distribution of parameter of the order τ=2 also have compared behaviour of stationary distribution to the results received in[30] (Figure [30]) for a case τ=1,5 in distribution exp{-U(s)}/Z. The results are shown in Figure 3. Calculation was carried out for the same values of parameters noise intensivity of energy I∑ and complexity Iζ which are used in[30]. Concurrence of the results, similar behaviour of distributions is evidenced. Parameters q, r0 only weakly influence behaviour of distribution. We shall note, that using the pure Tsallis distribution leads to another behaviour of stationary distribution (in particular, does not show indicated in[30] distinctions between distributions with I∑=1; Iζ=5 and I∑=0,5; Iζ=30).
from[30] for a case fluktuated formations of avalanches with an integer exponent of distribution of parameter of the order τ=2 also have compared behaviour of stationary distribution to the results received in[30] (Figure [30]) for a case τ=1,5 in distribution exp{-U(s)}/Z. The results are shown in Figure 3. Calculation was carried out for the same values of parameters noise intensivity of energy I∑ and complexity Iζ which are used in[30]. Concurrence of the results, similar behaviour of distributions is evidenced. Parameters q, r0 only weakly influence behaviour of distribution. We shall note, that using the pure Tsallis distribution leads to another behaviour of stationary distribution (in particular, does not show indicated in[30] distinctions between distributions with I∑=1; Iζ=5 and I∑=0,5; Iζ=30). 5. Conclusions
- The results of Sections 2-4 were investigated in[4-5]. From the distribution (5) containing lifetime of statistical system (time before degeneration of system) are obtained the superstatistics, entered in[1] in many respects is formal (though in[1] the dynamic bases is lead). In the present work obvious expression for β`=β0(1-r0)+r1β01 is obtained, the physical sense of distributions f1(β`) and f(αkβkPk/uk) is elucidated (besides distribution of return temperature), - as density of distribution of probability of destruction in the certain time interval, on k-th stages. It is possible for this reason gamma-distributions f(x)=λαxα-1 exp{-λx}/(α) with a parameter α=r/2 (is more true, χ2 distributions with r degrees of freedom which corresponds to gamma-distribution at λ=1/2-c; in[1] value r is interpreted as number of degrees of freedom giving the contribution in fluktuating value β) precisely describe Tsallis statistics, - they correspond to distribution of lifetime with r stages. Other variant of the obtained expressions forms at lnQ=βPV instead of β0PV as it was supposed after expression (21). Then β0=β(1+r0), β=β0/(1+r0), and correlations (22), (23) become the form P(E)=exp{-β0E/(1+r0)}ω(E)Z-1f(β01r1/(1+r0))exp{-β01r1E/(1+r0)} d(β01r1/(1+r0)); P(E)=exp{-β0E/(1+r0)}ω(E)Z-1[1+(q-1)β0r0E/(1+r0)]-1/(q-1). At r0→0, α→0, these distributions pass in Gibbs distribution, as in (22), (23). But in Tsallis distribution they pass at r0→∞, α→∞, γ→∞ as against (22), (23) where it occurs at r0=αP/u=1, α=u/P=γ/λ. Possible relation of values βq=β/=β/[1-(q-1)Sq][34] with β0=β/(1-r0) or β(1+r0) depends on a choice of β as well. Thus it is possible to find a relation between α and q. In[34] one more interesting question on a form of the differential equations for y(x)=P(E) is considered. For distribution (23) this equation looks like dP(E)/dE=-β0(1-r0)P(E)-β0r0P(E)/[1+(q-1)β0r0E]. It is possible to lead analogies to the equations which have been written down in[34]. The Gibbs distribution does not describe the dissipative processes that develop in the system. Superstatistics describe systems by constanly putting energy into the system which is dissipated. The value α=γ/λ is connected with dissipative processes in the system (through γ). She defines a correlation between Gibbs and superstatistics multipliers in distribution (22). It is possible not to pass to integrated relations, as in (22), having limited to summation (so, as discrete analogue of gamma-distribution negative binomial distribution serves). The discrete description in many cases, for example, for bistability potential, appears more precisely continuous. The found conformity between superstatics and the nonequilibrium distribution containing lifetime, should appear useful to both cases. For example, many results established for superstatistics and nonextensive statistical mechanics, are transferred to the description of complex systems by means of the distribution containing lifetime. Since thermodynamics with lifetime[4, 5] is more general, than the theory of superstatistiks also it has more opportunities. Interesting is establishing the relation to a method of the nonequilibrium statistical operator of Zubarev[11] generalizing Gibbs distributions which as it was marked, it is possible to compare to the distributions containing lifetime, and nonextensive statistical mechanics[2-3], in which entropy is represented by means of the measures which are distinct from Boltzmann and Gibbs. Probably, they stand close to the concept of lifetime, in the latent kind present in both theories. The relation γ=αλ (18) is of interest also. The value γ thermodynamical conjugated to random lifetime is expressed through entropy production and currents[12], i.e. through communication of system with an environment. It is shown, that the behaviour of the obtained distribution (22)-(23) interpolates between behaviour of Gibbs and Tsallis distributions. Application of this distribution to the phenomenon of the self-organized criticality (and other examples) shows his efficiency. The obtained distribution contains the new parameter related to a thermodynamic state of the system, and also with distribution of a lifetime of a metastable states and interaction of this states with an environment. Changing this parameter it is possible to pass to both Gibbs and Tsallis distributions.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML