Habibur Rahman 1, M. K. Roy 2, Atikur Rahman Baizid 1
1Department of Business Administration, Leading University, Sylhet. Bangladesh
2Department of Statistics, Chittagong University, Chittagong, Bangladesh
Correspondence to: Habibur Rahman , Department of Business Administration, Leading University, Sylhet. Bangladesh.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The Bayesian estimation approach is a non-classical device in the estimation part of statistical inference which is very useful in real world situation. The main objective of this paper is to study the Bayes estimators of the parameter of Power function distribution. In Bayesian estimation loss function, prior distribution and posterior distribution are the most important ingredients. In real life we try to minimize the loss and want to know some prior information about the problem to solve it accurately. The well known conjugate priors are considered for finding the Bayes estimator. In our study we have used different symmetric and asymmetric loss functions such as squared error loss function, quadratic loss function, modified linear exponential (MLINEX) loss function and non-linear exponential (NLINEX) loss function. The performance of the obtained estimators for different types of loss functions are then compared among themselves as well as with the classical maximum likelihood estimator (MLE). Mean Square Error (MSE) of the estimators are also computed and presented in graphs.
Keywords:
Squared Error Loss Function (SE), Modified Linear Exponential (MLINEX) Loss Function, Non-Linear Exponential (NLINEX) Loss Function, Maximum Likelihood Estimator (MLE)
1. Introduction
The Power function distribution is often used to study the electrical component reliability [3]. A continuous random variable X is said to have Power function distribution if its probability density function is given by [2]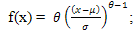
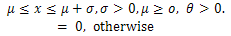 | (1) |
Where θ is the shape parameter, μ is the location parameter and σ is the scale parameter. We are interested to find Bayes estimator of shape parameter θ under different loss functions. Let μ = 0 and σ = 1 then the form of the density function becomes 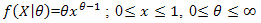 | (2) |
1.1. Prior and Posterior Density Function of
For Bayesian estimation we need to specify a prior distribution for the parameter. Consider a Gamma prior for θ having pdf[6] 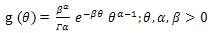 | (3) |
Now the Posterior density function of θ for the given random sample X is given by[4]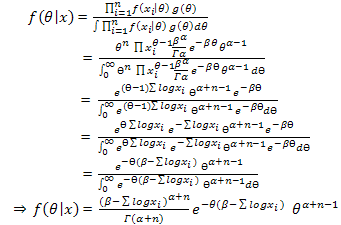 | (4) |
which implies that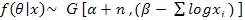 , since prior and posterior distribution belongs to the same family hence the prior is conjugate prior.
, since prior and posterior distribution belongs to the same family hence the prior is conjugate prior.
2. Different Estimators of Parameter θ
In this section Bayes estimators of parameter θ for different loss functions along with maximum likelihood estimator has been determined.
2.1. MLE of θ
Let X = 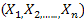 be a random sample of size n drawn from the Power function distribution defined in (2). Then the likelihood function of θ for the given random sample X is given by[4]
be a random sample of size n drawn from the Power function distribution defined in (2). Then the likelihood function of θ for the given random sample X is given by[4]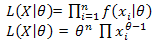 | (5) |
Taking log on both sides of (5) we get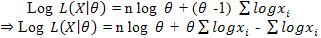 The MLE of θ will be the solution of the equation[4]
The MLE of θ will be the solution of the equation[4]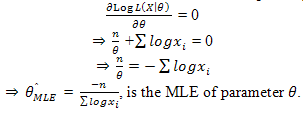
2.2. Bayes Estimator of θ for Squared Error Loss Function
Here we have determined Bayes estimator of θ for squared error loss function defined as[6]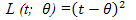 | (6) |
For squared error loss function Bayes estimator is the mean of posterior density function. From (4) posterior density function is a Gamma distribution with parameter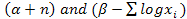 . Hence the mean of posterior density function is
. Hence the mean of posterior density function is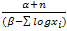 .Therefore
.Therefore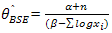 , is the Bayes estimator of θ under SE loss function.
, is the Bayes estimator of θ under SE loss function.
2.3. Bayes Estimator of θ for Quadratic Loss Function
Now suppose the loss function is quadratic, which is defined as[5]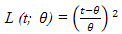 | (7) |
Under quadratic loss function Bayes estimator of θ is obtained by solving the following equation 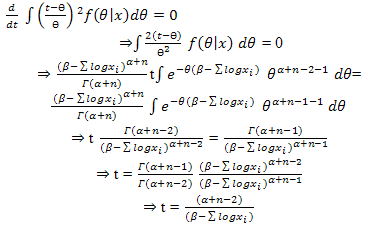 Therefore
Therefore 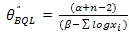 , is the Bayes estimator of θ under quadratic loss function
, is the Bayes estimator of θ under quadratic loss function
2.4. Bayes Estimator of θ for MLINEX Loss Function
Now let us consider the MLINEX loss function defined as [5]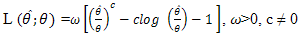 | (8) |
For MLINEX loss function Bayes estimator of θ is obtained from [5]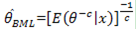 | (9) |
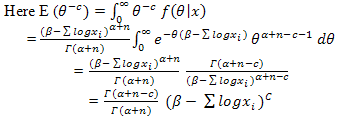 Hence from (9) we get
Hence from (9) we get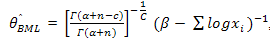 , is the Bayes estimator of θ under MLINEX loss function.
, is the Bayes estimator of θ under MLINEX loss function.
2.5. Bayes Estimator of θ for NLINEX Loss Function
Let us consider the following NLINEX loss function of the form [1]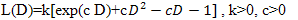 | (10) |
where D represents the estimation error .i.e. 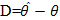 ; For NLINEX loss function Bayes estimator of θ is [1]
; For NLINEX loss function Bayes estimator of θ is [1] 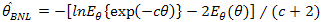 | (11) |
where 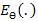 stands for posterior expectation. Now,
stands for posterior expectation. Now, 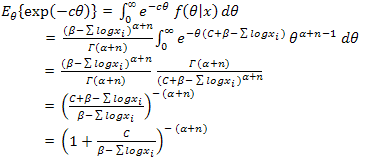 Therefore
Therefore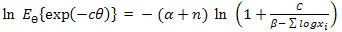 | (12) |
AgainUsing (12) and (13) in (11) we get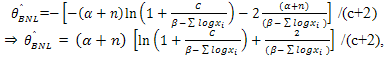 is the Bayes estimator of θ under NLINEX loss function.
is the Bayes estimator of θ under NLINEX loss function.
3. Empirical Study
To compare the estimators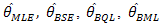 and
and 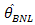 we have considered MSE of the estimators. The MSE of an estimator 𝜃 is defined as
we have considered MSE of the estimators. The MSE of an estimator 𝜃 is defined as 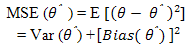 To obtain the variance of θ, we have used the true value of the parameter 𝜃 under consideration. We have obtained the estimated value, MSE and Bias of the estimator by using the Monte Carlo simulation method from the Power function distribution. Five thousand samples have taken for each case. The results and their graphs are presented bellow.From table 1 we observed that MSE of
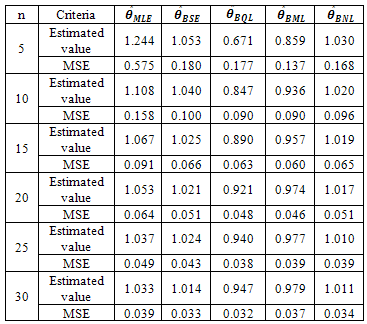
To obtain the variance of θ, we have used the true value of the parameter 𝜃 under consideration. We have obtained the estimated value, MSE and Bias of the estimator by using the Monte Carlo simulation method from the Power function distribution. Five thousand samples have taken for each case. The results and their graphs are presented bellow.From table 1 we observed that MSE of  is very high for small sample but declining sharply and becoming closer to other estimators with increasing sample size. Among Bayes estimators
is very high for small sample but declining sharply and becoming closer to other estimators with increasing sample size. Among Bayes estimators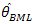 gives smaller value of MSE when sample size is small but for large sample they are almost identical (figure1).
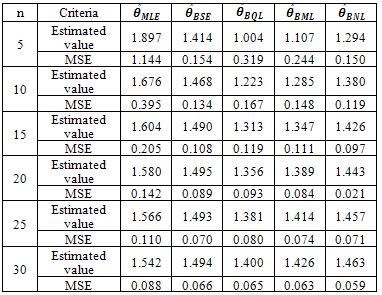
gives smaller value of MSE when sample size is small but for large sample they are almost identical (figure1).Table 1. Estimated value and MSE of different estimators of the parameter 𝜃 of Power function distribution when α =0.5, β=1, θ= 1 and c=1
 |
| |
|
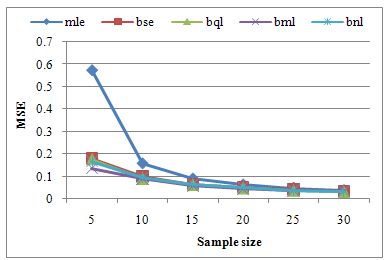 | Figure 1. Graph of MSEs of different estimates of parameter θ of Power function distribution when α=0.5, β=1, θ =1 and c=1 |
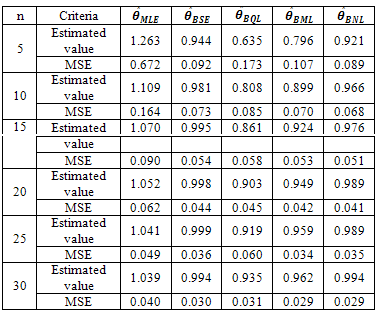
Table 2. Estimated value and MSE of different estimators of the parameter 𝜃 of Power function distribution when α =1, β=2, θ= 1 and c=1
 |
| |
|
Table 2 represents largest value of MSE for  in all cases. It is also clear from table 2 that MSE of
in all cases. It is also clear from table 2 that MSE of  is smallest than others estimators for different sample size (figure 2).
is smallest than others estimators for different sample size (figure 2). 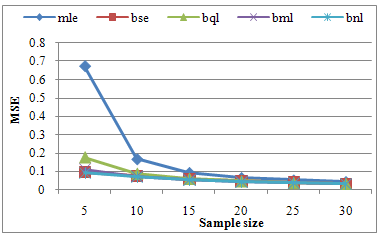 | Figure 2. Graph of MSEs of different estimates of parameter θ Power function distribution when α=1, β=2, θ =1 and c=1 |
Table 3. Estimated value and MSE of different estimators of the parameter 𝜃 of Power function distribution when α =2, β =2, θ =1.5 and c = 2
 |
| |
|
Table.3. shows the variation in the performance of the estimator for different sample size. More or less similar pattern are observed here as previous tables that is MSE of  is higher than all other estimators. MSE of
is higher than all other estimators. MSE of 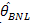 is least in the class of Bayes estimators. Also MSE of
is least in the class of Bayes estimators. Also MSE of 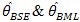 are very close to each other for large sample (figure 3)
are very close to each other for large sample (figure 3)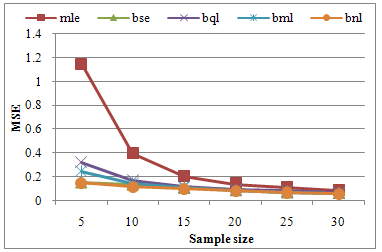 | Figure 3. Graph of MSEs of different estimates of parameter θ of Power function distribution when α=2, β=2, θ =1.5 and c=2 |
Table 4. Estimated value and MSE of different estimators of the parameter 𝜃 of Power function distribution when α =1.5, β=2, θ= 1.5 and c=2
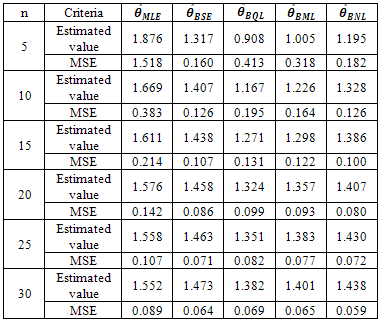 |
| |
|
For different sample size table 4 also shows minimum values of MSE for 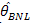 and some cases it is very near to that of
and some cases it is very near to that of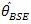 . On the other hand
. On the other hand  keep its tradition as previous cases.
keep its tradition as previous cases.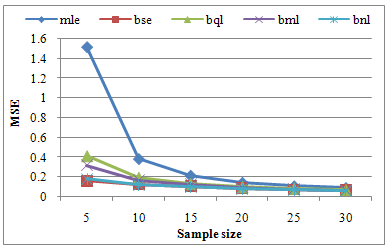 | Figure 4. Graph of MSEs of different estimates of parameter θ of Power function distribution when α=1.5, β=2, θ =1.5 and c=2 |
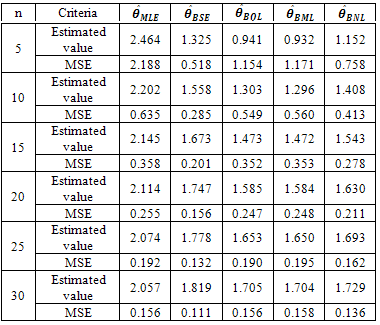
Table 5. Estimated value and MSE of different estimators of the parameter 𝜃 of Power function distribution when α =2, β=3, θ= 2 and c=3
 |
| |
|
Table 5 gives smaller values of MSE for 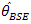 than all other estimators in the study. From the above table according to MSE the relation among the estimators is
than all other estimators in the study. From the above table according to MSE the relation among the estimators is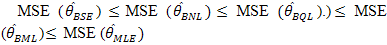
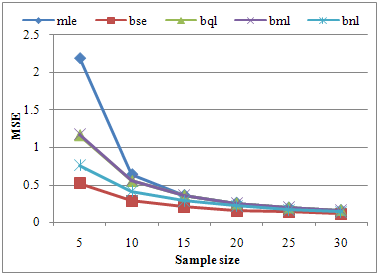 | Figure 5. Graph of MSEs of different estimates of parameter θ of Power function distribution when α=2, β=3, θ =2 and c=3 |
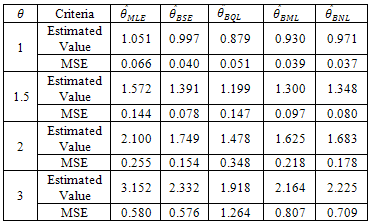
The performance of the estimators for different values of parameter θ are also shown in the table 6 along with their graphical presentation.Table 6. Estimated value and MSE of different estimators of the parameter 𝜃 of Power function distribution when n = 20 , α =2 , β = 3 and c = 2
 |
| |
|
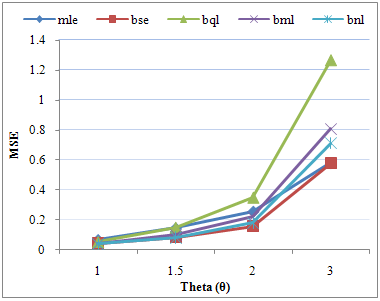 | Figure 6. Graph of MSEs of different estimates of parameter θ of Power function distribution when n=20, α=2, β=3 and c=2 |
4. Conclusions
From the above analysis and graphical study we can conclude that except for few cases Bayes estimator under NLINEX loss function and Squared Error loss function are better than other estimators in the study.
References
| [1] | F. M. Saiful Islam, M. K. Roy, M. Masoom Ali : Journal of Korean Data and Information Science Society 2004, Vol. 15, No. 4, pp.899~910. |
| [2] | Mbah, Alfred Kubong, "On the theory of records and applications". Theses and Dissertations. Paper 2282, 2007. |
| [3] | M. Meniconi, D. M. Barry; “Microelectronics Reliability”, volume 36, issue 9, pages 1207-1212, 1996. |
| [4] | M. Mood, A. Graybill, C. Boes; “Introduction to the Theory of Statistics”, Mc GRAW-Hill, Third Edition, 341. 279. |
| [5] | M. K. J. Bhuiyan, M.K. Roy, M. F. Imam; “Minimax Estimation of the Parameter of the Rayleigh Distribution”, pages 207-212, 2007. |
| [6] | S.K. Singh, Umesh Singh, Dinesh Kumar; Bayes Estimation of the Exponentiated Gamma Parameter and Reliability Function under Asymmetric Loss Function. revstat- Statistical Journal, Volume 9, Number 3, 247-260, 2011. |

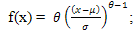
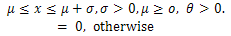
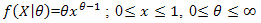
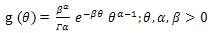
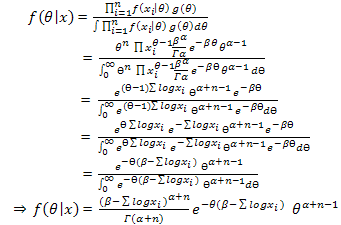
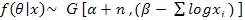 , since prior and posterior distribution belongs to the same family hence the prior is conjugate prior.
, since prior and posterior distribution belongs to the same family hence the prior is conjugate prior. 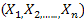 be a random sample of size n drawn from the Power function distribution defined in (2). Then the likelihood function of θ for the given random sample X is given by[4]
be a random sample of size n drawn from the Power function distribution defined in (2). Then the likelihood function of θ for the given random sample X is given by[4]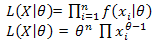
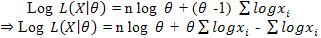 The MLE of θ will be the solution of the equation[4]
The MLE of θ will be the solution of the equation[4]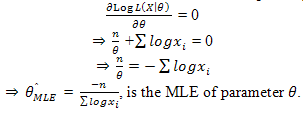
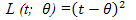
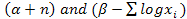 . Hence the mean of posterior density function is
. Hence the mean of posterior density function is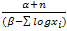 .Therefore
.Therefore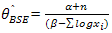 , is the Bayes estimator of θ under SE loss function.
, is the Bayes estimator of θ under SE loss function.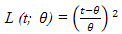
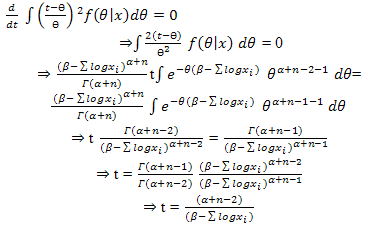 Therefore
Therefore 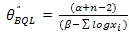 , is the Bayes estimator of θ under quadratic loss function
, is the Bayes estimator of θ under quadratic loss function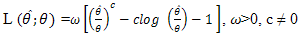
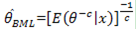
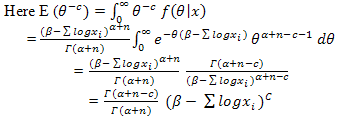 Hence from (9) we get
Hence from (9) we get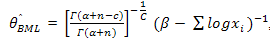 , is the Bayes estimator of θ under MLINEX loss function.
, is the Bayes estimator of θ under MLINEX loss function.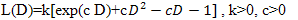
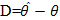 ; For NLINEX loss function Bayes estimator of θ is [1]
; For NLINEX loss function Bayes estimator of θ is [1] 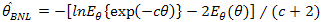
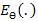 stands for posterior expectation. Now,
stands for posterior expectation. Now, 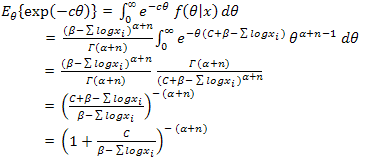 Therefore
Therefore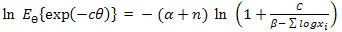
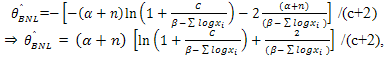 is the Bayes estimator of θ under NLINEX loss function.
is the Bayes estimator of θ under NLINEX loss function.  and
and 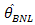 we have considered MSE of the estimators. The MSE of an estimator 𝜃 is defined as
we have considered MSE of the estimators. The MSE of an estimator 𝜃 is defined as 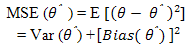 To obtain the variance of θ, we have used the true value of the parameter 𝜃 under consideration. We have obtained the estimated value, MSE and Bias of the estimator by using the Monte Carlo simulation method from the Power function distribution. Five thousand samples have taken for each case. The results and their graphs are presented bellow.From table 1 we observed that MSE of
To obtain the variance of θ, we have used the true value of the parameter 𝜃 under consideration. We have obtained the estimated value, MSE and Bias of the estimator by using the Monte Carlo simulation method from the Power function distribution. Five thousand samples have taken for each case. The results and their graphs are presented bellow.From table 1 we observed that MSE of  is very high for small sample but declining sharply and becoming closer to other estimators with increasing sample size. Among Bayes estimators
is very high for small sample but declining sharply and becoming closer to other estimators with increasing sample size. Among Bayes estimators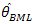 gives smaller value of MSE when sample size is small but for large sample they are almost identical (figure1).
gives smaller value of MSE when sample size is small but for large sample they are almost identical (figure1).
 in all cases. It is also clear from table 2 that MSE of
in all cases. It is also clear from table 2 that MSE of 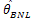 is smallest than others estimators for different sample size (figure 2).
is smallest than others estimators for different sample size (figure 2). 
 is higher than all other estimators. MSE of
is higher than all other estimators. MSE of 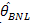 is least in the class of Bayes estimators. Also MSE of
is least in the class of Bayes estimators. Also MSE of 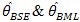 are very close to each other for large sample (figure 3)
are very close to each other for large sample (figure 3)
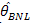 and some cases it is very near to that of
and some cases it is very near to that of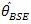 . On the other hand
. On the other hand  keep its tradition as previous cases.
keep its tradition as previous cases.
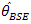 than all other estimators in the study. From the above table according to MSE the relation among the estimators is
than all other estimators in the study. From the above table according to MSE the relation among the estimators is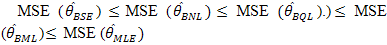


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML




