G. M. Moatimid , M.H.M. Moussa , Rehab M. El-Shiekh , A. A. El-Satar
Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Hiliopolis, Cairo, Egypt
Correspondence to: A. A. El-Satar , Department of Mathematics, Faculty of Education, Ain Shams University, Roxy, Hiliopolis, Cairo, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, Lie-Group method is applied to the b-family equations which includes two important nonlinear partial differential equations Camassa--Holm (CH) equation and the Degasperis--Procesi (DP) equation. The complete Lie algebra of infinitesimal symmetries is established. Three nonequivalent sub-algebras of the complete Lie algebra are used to investigate similarity solutions and similarity reductions in the form of nonlinear ordinary equations (ODEs) for the b-family equations. The generalized He's Exp-Function method is used to drive exact solutions for the reduced nonlinear ODEs, some figures are given to show the properties of the solutions.
Keywords:
Similarity Reductions, Lie-Group Method, Exact Solution
1. Introduction
In this paper we consider the following b-family of equations[1]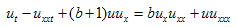 | (1.1) |
where b is a dimensionless constant. The quadratic terms in Eq. (1) represent the competition, or balance, in fluid convection between nonlinear transport and amplification due to b-dimensional stretching[2-3]. On the other hand, in a recent study of soliton equations, it was found that for any b≠-1, Eq. (1) was included in the family of shallow water equations at quadratic order accuracy that are asymptotically equivalent under Kodama transformations[4].Degasperis and Procesi[5] showed that the family of equations (1) cannot be integrable unless b=2 or b=3 by using the method of asymptotic integrability. The previous two values of b are corresponding to two important equations the Camassa--Holm (CH) equation and the Degasperis-- Procesi (DP) equation respectively. The CH and the DP equations are bi-Hamiltonian and have an associated isospectral problem, therefore they are both formally integrable[6-9]. Moreover, both equations admit peaked solitary wave solutions and present similarities although they are truly different[10-13].
2. Solution of the Problem
Firstly, we shall derive the similarity solutions using the Lie group method[14] under which Eq. (1.1) is invariant in the following steps:1- Lie point symmetries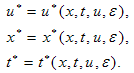 | (2.1) |
With associated infinitesimal form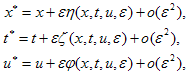 | (2.2) |
2- If we set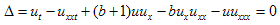 | (2.3) |
Then the invariance condition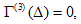 | (2.4) |
where 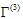 is given by
is given by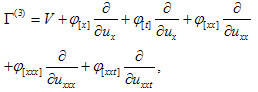 | (2.5) |
where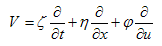 | (2.6) |
The components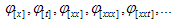 | (2.7) |
can be determined from the following expressions: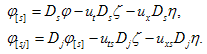 | (2.8) |
Eq. (2.4) gives the following system of linear partial differential equations: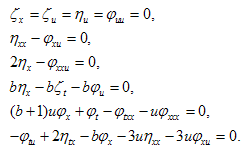 | (2.9) |
3- The general solution of Eqs. (2.9) provides following forms for the infinitesimal element ζ,η and φ: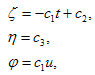 | (2.10) |
where c1,c2 and c3are arbitrary constant.4- In order to study the group theoretic structure, the vector field operator V is written as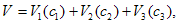 | (2.11) |
where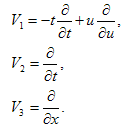 | (2.12) |
It is easy to verify the vector fields are closed under the Lie bracket as follows: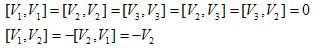 Furthermore, we can compute the adjoint representations of the vector fields
Furthermore, we can compute the adjoint representations of the vector fields 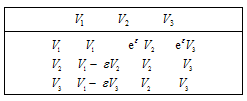 From the previous adjoint representations we have the following three non-equivalent possibilities of sub-algebras of the Lie algebra (I) V1+V3.(II) V2+V3.(III) V1.Now we could determine the similarity variables and similarity reduction corresponding each vector field using the auxiliary equation
From the previous adjoint representations we have the following three non-equivalent possibilities of sub-algebras of the Lie algebra (I) V1+V3.(II) V2+V3.(III) V1.Now we could determine the similarity variables and similarity reduction corresponding each vector field using the auxiliary equation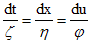 | (2.13) |
3. Similarity Reduction and Exact Solutions
In this section, the primary focus is on the reductions association with the vector fields (I-III) and attempt to some exact solutions:Vector field V1+V3For this vector field, on using the characterstic Eq. (2.13), the similarity variable and the form of similarity solution is as follows: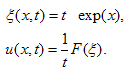 | (3.1) |
On using these in Eq. (1.1), the reduced ODE is given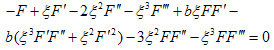 | (3.2) |
where prime (′) denotes the differentiation with respect to the variable ξ. On transforming the independent variable by the relation ξ=exp(τ) Eq. (3.2) becomes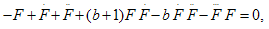 | (3.3) |
where dot denotes the defferentiation with respect to variable τ. In view of the generalized He's Exp-Function method[15], we assume that the solution of Eq. (3.3) can be expressed in the form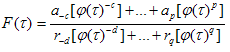 | (3.4) |
where c, d, p and q are positive integers which are unknown to be further determined, an and rm are unknown constants. In addition, φ(τ) satisfies Riccati equation,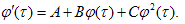 | (3.5) |
In order to determine values of c and p, we balance the linear term of the highest order in Eq. (3.3), we have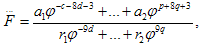 | (3.6) |
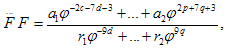 | (3.7) |
where ai and ri are determined coefficients only for simplicity. From balancing the lowest order and highest order of φ (3.6) and (3.7), we obtain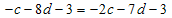 | (3.8) |
which leads to the limit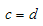 | (3.9) |
and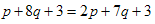 | (3.10) |
which leads to the limit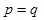 | (3.11) |
For simplicity, we set p = c = 1, the trial function, Eq. (3.4), becomes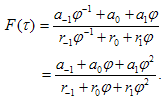 | (3.12) |
Substituting Eq. (3.12) into Eq. (3.3), equating to zero the coefficients of all powers of φ(τ) yields a set of algebraic equations for a₀, r₀, a0, r1, a-1 and r-1 . Solving the system of algebraic equations with the aid of Maple, where A=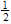 , B=0, C=
, B=0, C=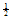 in Eq.(2.18), we obtain the following results:
in Eq.(2.18), we obtain the following results:  b is arbitrarySubstituting the results of case I into (3.12), the solutions of Eq.(1.1) can be written as:
b is arbitrarySubstituting the results of case I into (3.12), the solutions of Eq.(1.1) can be written as: | (3.13) |
where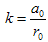 .Vector field V2+V3For this generator the associated similarity variable and similarity solution are given by:
.Vector field V2+V3For this generator the associated similarity variable and similarity solution are given by: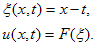 | (3.14) |
On using these in Eq. (1.1), the reduced ODE is given by 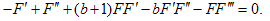 | (3.15) |
Be using the ansatz (3.14), the solution of Eq. (1.1) can be writen as: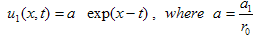
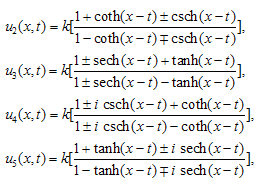 | (3.16) |
where 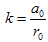 Vector field V1The generator (III) in the optimal system defines the similarity variable and similarity solution as follows:
Vector field V1The generator (III) in the optimal system defines the similarity variable and similarity solution as follows: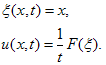 | (3.17) |
On using these in Eq. (1.1), the reduced ODE is given by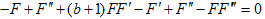 | (3.18) |
Using the ansatz (3.14), we have the following solutions: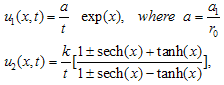
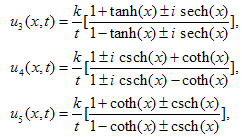 | (3.19) |
where 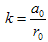
4. Conclusions
In summary, we have utilized this method to construct new exact solutions for b-family equations. In solutions (3.13) and (3.19) there is singularity at t=0, so we put t≻0 in figures. All solutions have been obtained in this paper for the b-family equations are also solutions for the CH and DP equations because those solutions were not restricted with any value of b.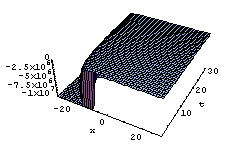 | Figure 1. solution of u1 (x,t) in (26), where k=1 |
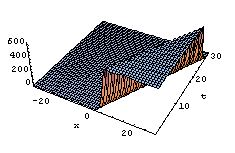 | Figure 2. solution u1 (x,t) in (29), where k=1 |
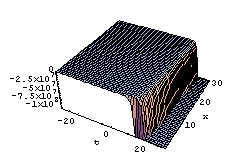 | Figure 3. solution u1 (x,t) in (29), where k=1 |
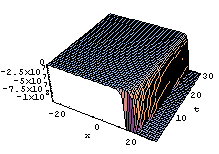 | Figure 4. solution u1 (x,t) in (32), where k=1 |
References
| [1] | A. Degasperis, D.D. Holm, A.N.W. Hone, Theoret. and Math. Phys. 133 (2002) 170-183. |
| [2] | A. Degasperis, D.D. Holm, A.N.W. Hone, II (Gallipoli, 2002), 37.43, World Sci. Publishing, River Edge, NJ, 2003. |
| [3] | H.R. Dullin, G.A. Gottwald, D.D. Holm, Phys. Rev. Lett. 87 (2002) 4501. 4504. |
| [4] | Degasperis A and Procesi M, Rome, December 1998, World Scienti.c, River Edge, NJ, 1999, 23-37. |
| [5] | Camassa R and Holm D, Phys. Rev. Lett. 71 (1993), 1661-1664. |
| [6] | Constantin A, Proc. R. Soc. London Ser. A - Math. Phys. Eng. Sci., 457 (2001), 953.970. |
| [7] | Constantin A and McKean H P, Comm. Pure Appl. Math. 52 (1999), 949.982. |
| [8] | Lenells J, J. Non-linear Math. Phys. 9 (2002), 389.393. |
| [9] | Fuchssteiner B and Fokas A S, Phys. D 4 (1981), 47.66. |
| [10] | Constantin A and Molinet L, Comm. Math. Phys. 211 (2000), 45.61. |
| [11] | Constantin A and Strauss W, Comm. Pure Appl. Math. 53 (2000), 603-610. |
| [12] | Octavian G Mustafa. Non linear Math. Phys.12 (1) (2005)10-14. |
| [13] | P.J. Olver, New York (1986). |
| [14] | A. El-Halim Ebaid, znaturforsch, 2009 |

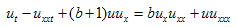
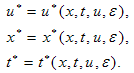
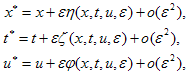
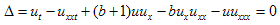
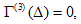
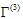 is given by
is given by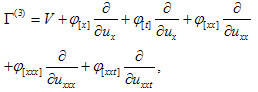
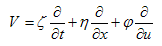
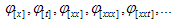
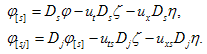
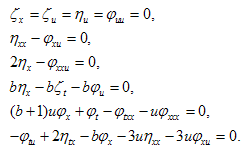
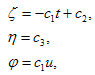
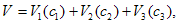
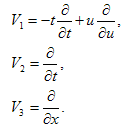
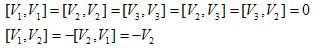 Furthermore, we can compute the adjoint representations of the vector fields
Furthermore, we can compute the adjoint representations of the vector fields 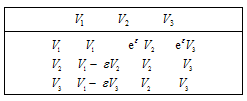 From the previous adjoint representations we have the following three non-equivalent possibilities of sub-algebras of the Lie algebra (I) V1+V3.(II) V2+V3.(III) V1.Now we could determine the similarity variables and similarity reduction corresponding each vector field using the auxiliary equation
From the previous adjoint representations we have the following three non-equivalent possibilities of sub-algebras of the Lie algebra (I) V1+V3.(II) V2+V3.(III) V1.Now we could determine the similarity variables and similarity reduction corresponding each vector field using the auxiliary equation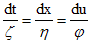
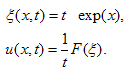
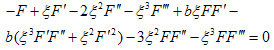
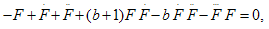
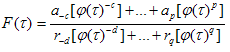
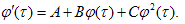
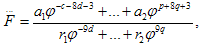
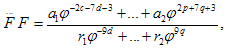
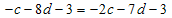
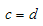
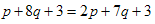
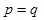
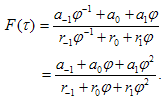
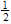 , B=0, C=
, B=0, C=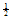 in Eq.(2.18), we obtain the following results:
in Eq.(2.18), we obtain the following results: 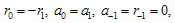 b is arbitrarySubstituting the results of case I into (3.12), the solutions of Eq.(1.1) can be written as:
b is arbitrarySubstituting the results of case I into (3.12), the solutions of Eq.(1.1) can be written as:
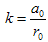 .Vector field V2+V3For this generator the associated similarity variable and similarity solution are given by:
.Vector field V2+V3For this generator the associated similarity variable and similarity solution are given by: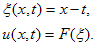
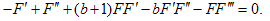
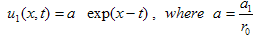
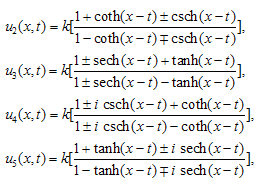
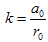 Vector field V1The generator (III) in the optimal system defines the similarity variable and similarity solution as follows:
Vector field V1The generator (III) in the optimal system defines the similarity variable and similarity solution as follows: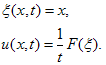
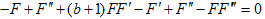
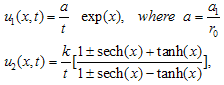
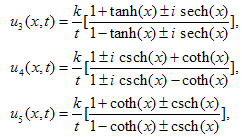
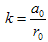




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML