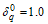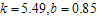Muhammad Aslam 1, Y. L. Lio 2, Muhammad Azam 1, Chi-Hyuck Jun 3
1Department of Statistics, Forman Christian College University, Lahore, Pakistan
2Department of Mathematical Sciences, University of South Dakota, USA
3Department of Industrial and Management Engineering, POSTECH, Pohang, 790-784, Republic of Korea
Correspondence to: Muhammad Aslam , Department of Statistics, Forman Christian College University, Lahore, Pakistan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper, we present two-stage group plan for Burr type XII distribution using lifetime percentile as quality parameter. The plan parameters such as acceptance number and group size are determined by considering producer’s risk and consumer’s risk at the same time. To find the plan parameters, we fixed the number of testers, experiment time and percentiles ratio. Many useful tables are generated for Burr type XII distribution as well as for log-logistic distribution. Two industrial examples are presented for the illustration of the proposed two-stage group sampling plan. Comparison of proposed plan with single-stage group plan is also discussed. Generally, the proposed two-stage sampling plan needs less number of test items than single-stage group plan does.
Keywords:
Two Stage Group Plans, Life Tests, Percentile Life, Burr Type XII Distributions, Producer and Consumer Risks
1. Introduction
The main aim of acceptance sampling plans is to reduce the inspection cost and provides the protection to producer and costumer. In this modern era, even some advance techniques including the quality assurance and quality control chats are available to improve the quality of the products but these techniques alone are incapable to achieve the product quality according to the customer specification. Especially, for electronic components testing, acceptance sampling schemes for life time experiments are widely used. Today, acceptance sampling schemes are widely used in industries for the testing purpose; for example, the application of an acceptance sampling scheme in food industry can be found in Bray and Lyon[1] and applications of acceptance sampling plans in testing of fiber optical can be found in Bhaumik and Bhargava[2]. Many acceptance sampling schemes including single and double acceptance sampling plans, have been widely used in industries. In the single acceptance sampling plan, decision about the lot is finalized on the basis of single sample selected from the production lot. A double acceptance sampling plan is used after the inspection of the first sample and an experimenter is not able to reach on the final decision about the submitted product. Then the second sample is selected from the lot to make decision about the submitted product. It is important to notice that acceptance sampling plans can mislead the experimenter. For example, using the acceptance sampling schemes, there is a chance to accept the bad lot or reject the good lot. So, the acceptance sampling plans are used to minimize these misclassification probabilities. Accepting the bad lot is called consumer’s risk and rejecting a good lot is called the producer’s risk. Acceptance sampling plans based on truncated life tests have been studied by many authors including Kantam et al.[3], Baklizi[4], Balakrishnan et al.[5] and Tsai and Wu[6].Double acceptance sampling is more useful to minimize the producer’s risk than the single acceptance sampling schemes. Double acceptance sampling is more efficient in reducing the number of items for inspection than the single acceptance sampling. Aslam and Jun[7] proposed the double acceptance sampling plan for generalized log-logistic distributions with known shape parameter.Group acceptance sampling plans are the extension of the ordinary acceptance sampling plans and widely used in the laboratory which has facility to install more than one item in a single tester. Group acceptance sampling plans are useful to reduce inspection cost and provide more strict inspection than single acceptance sampling plans. The group plans are widely used in sudden death testing. Jun et al.[8] proposed the variable sampling plans for Weibull distribution using the sudden death testing scheme. Aslam and Jun[9] originally proposed the group plan for time truncated experiment for Weibull distribution using two points approach. Two stage group plans are extension of the single stage group plans. Recently, Aslam et al.[10] proposed the improved version of single stage group plan and two-stage group plan based on total failures from all the groups. They declared that the improved version of single stage group plan and two-stage group plan based on total failures from all the groups are more efficient than the ordinary acceptance sampling plans.All the aforementioned works in the area of acceptance sampling plans were developed by using the mean life time of the distribution. But, recently, Lio et al.[11, 12] developed the acceptance sampling plans for the lifetime percentiles. They argued that mean lifetime of the product may not satisfy the requirement of engineering design consideration. Acceptance sampling plans developed using mean life could pass a lot which has a low percentile below the required specification. Further, the Burr type XII distribution is skewed distribution and as stated Marshall and Olkin[13] that as a quality parameter the mean life does not perform well than the lifetime percentiles if the distribution under study is skewed. The works for developing acceptance sampling plans for the lifetime percentiles are an extended research works for developing the acceptance sampling plans for the mean life and for the median.According to best of our knowledge, two-stage group sampling plans based on the Burr type XII distribution percentiles have not seen in literatures. The purpose of this paper is to develop the two-stage group plans for the Burr XII distribution percentiles.The Burr type XII distribution has the cumulative distribution function (cdf) as follows: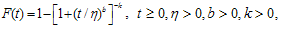 where
where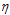 is the scale parameter,
is the scale parameter, 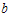 and
and 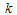 are the two shape parameters. When k=1, the burr type XII distribution converts to the log-logistic distribution. The 100
are the two shape parameters. When k=1, the burr type XII distribution converts to the log-logistic distribution. The 100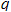 -th percentile of the burr type XII distribution is given as:
-th percentile of the burr type XII distribution is given as: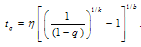 The rest of the paper is organized as follows, the design of the proposed plans and some of tables used for discussions are given in Section 2. Two applications in industrial are presented in Section 3. Section 4 compares the proposed two-stage sampling plan with sign stage sampling plan and concluding remarks are given at the end.
The rest of the paper is organized as follows, the design of the proposed plans and some of tables used for discussions are given in Section 2. Two applications in industrial are presented in Section 3. Section 4 compares the proposed two-stage sampling plan with sign stage sampling plan and concluding remarks are given at the end.
2. Design of Two-Stage Group Plan Using Percentiles
In this section, the design of two-stage group sampling plan for Burr XII distribution percentiles is described by followed Aslam et al.[7]
2.1. Improved Two Stage Group Sampling Plan
1. (First stage) Draw the first random sample of size 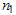 from a lot, allocate
from a lot, allocate 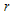 items to each of
items to each of 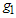 groups (or testers) so that
groups (or testers) so that 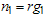 and put them on test for the duration of
and put them on test for the duration of 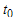 units of time. Accept the lot if the total number of failures from
units of time. Accept the lot if the total number of failures from 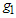 groups is smaller than or equal to
groups is smaller than or equal to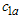 . Truncate the test and reject the lot as soon as the total number of failures is larger than or equal to
. Truncate the test and reject the lot as soon as the total number of failures is larger than or equal to 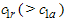 during the
during the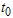 units of time. Otherwise, go to the second stage.2. (Second stage) Draw the second random sample of size
units of time. Otherwise, go to the second stage.2. (Second stage) Draw the second random sample of size 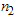 from the lot, allocate
from the lot, allocate 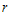 items to each of
items to each of 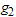 groups so that
groups so that 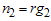 and put them on test for the duration of
and put them on test for the duration of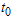 units of time again. Accept the lot if the total number of failures from
units of time again. Accept the lot if the total number of failures from 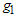 and
and 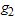 groups is smaller than or equal to
groups is smaller than or equal to 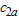 (>
(>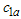 ). Otherwise, truncate the test and reject the lot.The proposed double group sampling plan is characterized by five design parameters, namely,
). Otherwise, truncate the test and reject the lot.The proposed double group sampling plan is characterized by five design parameters, namely, 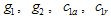 and
and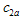 .It should be noticed that the proposed group sampling plan is different from the double acceptance sampling plans studied by Aslam et al.[14]. When
.It should be noticed that the proposed group sampling plan is different from the double acceptance sampling plans studied by Aslam et al.[14]. When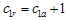 , the total number of failures from
, the total number of failures from 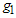 groups (denoted by
groups (denoted by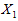 ) follows a binomial distribution with parameters
) follows a binomial distribution with parameters 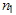 and
and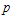 . Therefore, the lot acceptance probability at the first stage under the proposed double sampling plan is given by Aslam et al.[10].
. Therefore, the lot acceptance probability at the first stage under the proposed double sampling plan is given by Aslam et al.[10].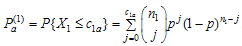 | (1) |
The lot rejection probability at the first stage is given by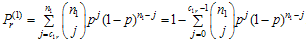 | (2) |
Now, the lot will be accepted from the second stage if the decision has not been made at the first stage and the total number of failures from 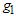 and
and 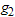 groups (denoted by
groups (denoted by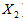 ) is smaller than or equal to
) is smaller than or equal to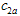 . Hence according to Aslam et al.[10],
. Hence according to Aslam et al.[10],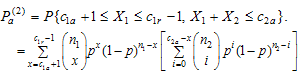 | (3) |
Therefore, the lot acceptance probability for the proposed double group sampling plan is given by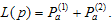 | (4) |
It would be convenient to determine the termination time 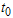 as a multiple of the specified percentile
as a multiple of the specified percentile 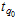 such that
such that 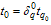 for a constant
for a constant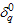 . For example
. For example 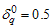 means that the experiment time is just half of the specified life percentile. The
means that the experiment time is just half of the specified life percentile. The 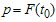 in terms of the 100q-th percentile of the Burr type XII distribution can be presented aswhere
in terms of the 100q-th percentile of the Burr type XII distribution can be presented aswhere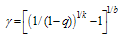 | (6) |
Particularly, the 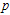 in terms of the median life is represented as
in terms of the median life is represented as 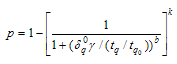 | (7) |
Where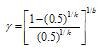 | (8) |
When the quality level based on the percentile ratio 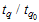 between the true percentile
between the true percentile 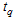 and targeted percentile
and targeted percentile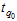 , the two-point approach of finding the design parameters is to determine the minimum number of groups,
, the two-point approach of finding the design parameters is to determine the minimum number of groups, 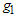 and
and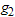 , and acceptance numbers,
, and acceptance numbers, 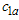 ,
, 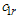 and
and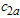 , to satisfy the following two inequalities
, to satisfy the following two inequalities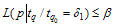 | (9) |
where, 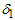 is the percentile ratio at the consumer’s risk and
is the percentile ratio at the consumer’s risk and 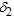 is the percentile ratio at the producer’s risk. Let
is the percentile ratio at the producer’s risk. Let 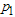 and
and 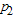 are the failure probabilities of corresponding to consumer’srisk and producer’s risk, respectively. The ASN under LTRL,
are the failure probabilities of corresponding to consumer’srisk and producer’s risk, respectively. The ASN under LTRL, 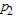 , is given by
, is given by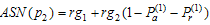 | (11) |
Then the optimization problem to be considered is as follows:Minimize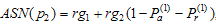 | (12a) |
subject to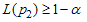 | (12b) |
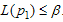 | (12c) |
Therefore, given 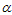 and
and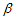 , the percentile ratio,
, the percentile ratio, 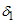 , at the consumer’s risk and the percentile ratio,
, at the consumer’s risk and the percentile ratio, 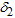 , at the producer’s risk, the design parameters of the proposed plan are determined such that the
, at the producer’s risk, the design parameters of the proposed plan are determined such that the 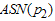 is minimized and inequalities (12b) and (12c) are satisfied simultaneously for specified values of shape parameters,
is minimized and inequalities (12b) and (12c) are satisfied simultaneously for specified values of shape parameters, 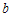 and
and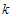 , termination ratio
, termination ratio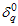 and the number of testers,
and the number of testers, 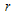 .If the shape parameters,
.If the shape parameters, 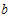 and
and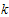 , are unknown, then the previous data information could be used to estimate these parameters.
, are unknown, then the previous data information could be used to estimate these parameters.
2.2. Tables for Two Stage Group Sampling Plan
Let 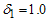 and
and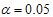 , the design parameters,
, the design parameters, 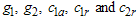 ,
, 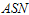 for the proposed plan as well as the probability of acceptance of the product are obtained for the ten percentiles of many Burr type XII distributions under each combination of
for the proposed plan as well as the probability of acceptance of the product are obtained for the ten percentiles of many Burr type XII distributions under each combination of 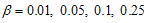 and
and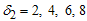 . Table 1 contains the results for the Burr type XII distribution with
. Table 1 contains the results for the Burr type XII distribution with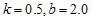 ; Table 2 has the results for the Burr type XII distribution with
; Table 2 has the results for the Burr type XII distribution with 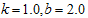 which is also called log-logistic distribution; Table 3 shows the results for the Burr type XII distribution with
which is also called log-logistic distribution; Table 3 shows the results for the Burr type XII distribution with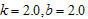 ; Table 4 displays the results for the Burr type XII distribution with
; Table 4 displays the results for the Burr type XII distribution with 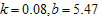 and the results for the Burr type XII distribution with
and the results for the Burr type XII distribution with 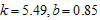 are placed in Table 5.From Tables 1-5, it can be noticed the following important trends in the design parameters and
are placed in Table 5.From Tables 1-5, it can be noticed the following important trends in the design parameters and
Table 1. Proposed two stage group sampling plan for Burr Type XII distribution k =0.5, b=2.0and
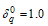
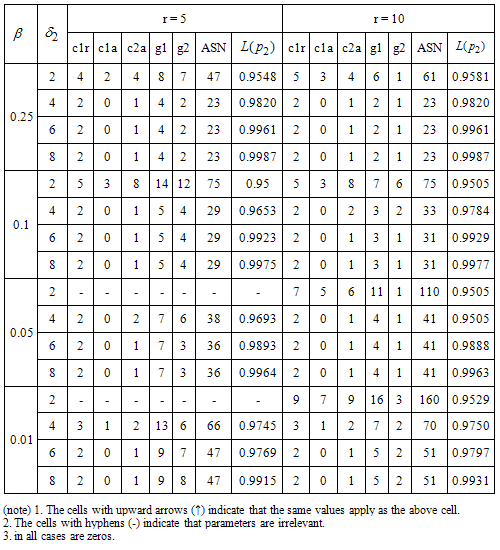 |
| |
|
Table 2. Proposed two stage group sampling plan for Burr Type XII distribution k =1.0,b=2.0 (log-logistic distribution)and
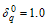
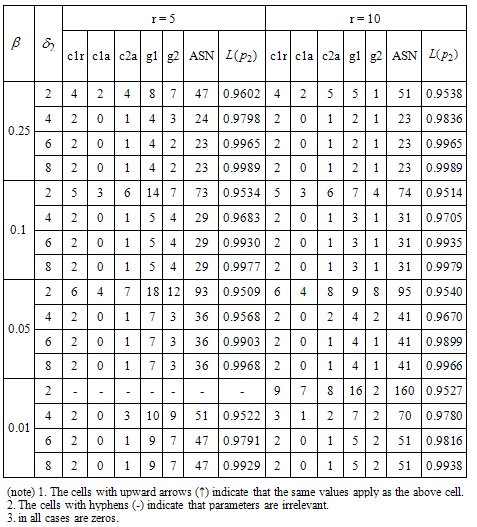 |
| |
|
Table 3. Proposed two stage group sampling plan for Burr Type XII distribution k =2.0,b=2.0and
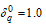
 |
| |
|
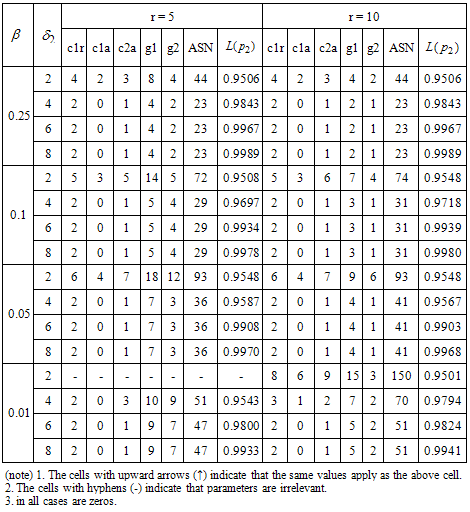
Table 4. Proposed two stage group sampling plan for Burr Type XII distribution k =0.08,b=5.47and
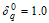 . .
 |
| |
|
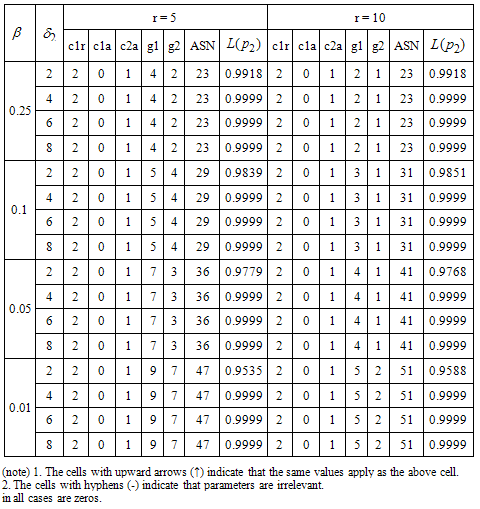
Table 5. Proposed two stage group sampling plan for Burr Type XII distribution k =5.49,b =0.85 and
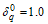
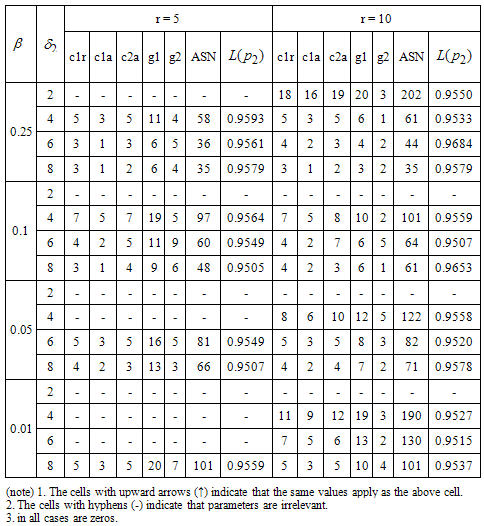 |
| |
|
Table 6. Minimum number of groups and acceptance number for the total failure plan for the Burr type XII distribution
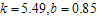
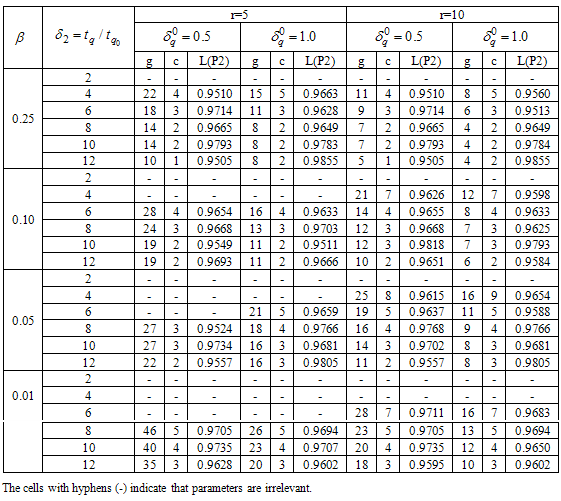 |
| |
|
1. For given β and the group size 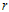 in each table, all the design parameters and
in each table, all the design parameters and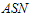 are non-increasing with respect to the percentile ratio
are non-increasing with respect to the percentile ratio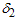 2. When the group size increases from 5 to 10, the numbers of groups for both stages are generally decreased for a given β and the percentile ratio
2. When the group size increases from 5 to 10, the numbers of groups for both stages are generally decreased for a given β and the percentile ratio 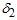 3. When the group size increases from 5 to 10,
3. When the group size increases from 5 to 10, 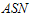 generally non-decreases for a given β and the percentile ratio
generally non-decreases for a given β and the percentile ratio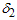 .4. When β increases, the numbers of groups for both stages are generally decreased for given group size
.4. When β increases, the numbers of groups for both stages are generally decreased for given group size 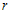 and the percentile ratio
and the percentile ratio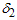 .
.
3. Applications of Industry
In this section, two industrial examples are used to demonstrate the applications of the proposed two-stage acceptance sampling plans.Example-1Lio et al. (2010) showed that the lifetime of small electric carts have a Burr type XII distributionwith k =0.08 and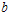 =5.47. Suppose that an experimenter would like to use the proposed two-stage sampling plan to establish the true unknown 10th percentile lifetime for the product is at least 4 months and experiment will be stopped after 4 months. Further, suppose that in the laboratory the experimenter has facility to install five items on a tester. This information leads to
=5.47. Suppose that an experimenter would like to use the proposed two-stage sampling plan to establish the true unknown 10th percentile lifetime for the product is at least 4 months and experiment will be stopped after 4 months. Further, suppose that in the laboratory the experimenter has facility to install five items on a tester. This information leads to 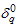 =1.0. Let β =0.01 and
=1.0. Let β =0.01 and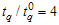 with
with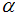 =0.05 for this experiment. Then from Table 4, the plan parameters are
=0.05 for this experiment. Then from Table 4, the plan parameters are 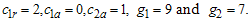 The two-stage acceptance sampling plan is implemented as follows: randomly select 45 items and distribute five items into each tester and accept the product if no failure is recorded in 4 months and reject the product if more than 1 failure is recorded before 4 months; otherwise, randomly select another 35 items from the lot and distribute five items into each tester. If the total number of failure items from the two-stage testing within four months for each stage is less than 2 then the lot is accepted; otherwise, the lot is rejected. According to this two-stage sampling plan, the experiment must be repeated when the number of failure is 1 from the first-stage test for four months. The probability of acceptance for this plan is 99.99% and
The two-stage acceptance sampling plan is implemented as follows: randomly select 45 items and distribute five items into each tester and accept the product if no failure is recorded in 4 months and reject the product if more than 1 failure is recorded before 4 months; otherwise, randomly select another 35 items from the lot and distribute five items into each tester. If the total number of failure items from the two-stage testing within four months for each stage is less than 2 then the lot is accepted; otherwise, the lot is rejected. According to this two-stage sampling plan, the experiment must be repeated when the number of failure is 1 from the first-stage test for four months. The probability of acceptance for this plan is 99.99% and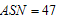 .Example-2Lio et al.[12] showed that the lifetime of oil breakdown of an insulating fluid under hightest voltage follows the Burr type XII distribution with k =5.49 and
.Example-2Lio et al.[12] showed that the lifetime of oil breakdown of an insulating fluid under hightest voltage follows the Burr type XII distribution with k =5.49 and 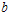 =0.85. Suppose that an experimenter would like to use the proposed two-stage sampling plan to establish the true unknown 10th percentile lifetime for the product is at least 6 months and experiment will be stopped after 6 months. Further suppose that the in laboratory the experimenter has facility to install ten items on a single tester. This information leads to
=0.85. Suppose that an experimenter would like to use the proposed two-stage sampling plan to establish the true unknown 10th percentile lifetime for the product is at least 6 months and experiment will be stopped after 6 months. Further suppose that the in laboratory the experimenter has facility to install ten items on a single tester. This information leads to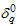 =1.0. Let β=0.05 and
=1.0. Let β=0.05 and 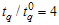 with
with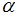 =0.05 for this experiment. Then from Table 5 with
=0.05 for this experiment. Then from Table 5 with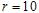 , the two-stage acceptance sampling plan parameters are
, the two-stage acceptance sampling plan parameters are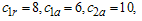
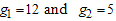 The sampling plan is implemented as follows: randomly select 120 items and distribute into ten testers such that tenitems on a single tester. Accept the product lot if less than seven failure items are recorded in 6 months and reject the product if more than 7 failures is recorded before 6 months. Otherwise, randomly select another 50 items and distribute into five testers evenly and test for 6 months. If the total number of failures from both stages is less than 11, then the lot is accepted; otherwise, the lot is rejected. From Table 5, the probability of acceptance is 95.58% and ASN =122 for this plan.
The sampling plan is implemented as follows: randomly select 120 items and distribute into ten testers such that tenitems on a single tester. Accept the product lot if less than seven failure items are recorded in 6 months and reject the product if more than 7 failures is recorded before 6 months. Otherwise, randomly select another 50 items and distribute into five testers evenly and test for 6 months. If the total number of failures from both stages is less than 11, then the lot is accepted; otherwise, the lot is rejected. From Table 5, the probability of acceptance is 95.58% and ASN =122 for this plan.
4. Comparison of Plans
In this section, the proposed two-stage acceptance sampling plan is compared with a single stage acceptance sampling plan. It should be noticed that we cannot compare these two acceptance sampling plans by using the sample size, since the two-stage sampling plan could have a chance to use the first stage to make a decision. Therefore, the minimum sample size needed for a single sampling plan will be used to compared with the 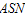 for the two-stage sampling plan. To save space, only the comparison for the Burr type XII with parameters
for the two-stage sampling plan. To save space, only the comparison for the Burr type XII with parameters 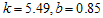 is displayed in this section. Table 6 shows the minimum number of groups and acceptance number for the total number of failures and
is displayed in this section. Table 6 shows the minimum number of groups and acceptance number for the total number of failures and 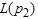 for single stage acceptance sampling plan. It could be noticed from Table 5 and Table 6, the proposed two-stage sampling plan generally has
for single stage acceptance sampling plan. It could be noticed from Table 5 and Table 6, the proposed two-stage sampling plan generally has 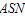 less than the sample size needed for a single sampling plan under the given rest conditions in both Tables 5 and 6.
less than the sample size needed for a single sampling plan under the given rest conditions in both Tables 5 and 6.
5. Conclusions
In this paper, a two-stage grouped acceptance sampling plan is developed for Burr type XII percentiles under the truncated life testing. Many useful tables for the proposed two-stage grouped acceptance sampling plans have been obtained for practical applications and two industrial examples have been presented to illustrate the applications of the proposed two-stage grouped sampling plan. The comparison between the proposed two-stage grouped acceptance sampling plan and single-stage acceptance sampling plan show that the proposed two-stage grouped acceptance sampling plan generally needs less test items than single-stage grouped acceptance sampling plan does.
Acknowledgements
The writers are deeply thankful to the editor and the reviewers for several valuable suggestions.
References
| [1] | Bray, D. F., Lyon, D. A. (1973). Three class attributes plans in acceptance sampling, Technometrics, 15, 575-585. |
| [2] | Bhaumik, S., and Bhargava, K. (2005). Applications of ac-ceptance sampling in testing of optical fiber , proceeding of International Conference on Optic and Optoelectronic, IRDE, Dehradun ,India, 12-15. |
| [3] | Kantam, R.R.L., Rosaiah, K., Rao, G.S. (2001). Acceptance sampling based on life tests: Log-logistic models. Journal of Applied Statistics, 28, 121-128. |
| [4] | Baklizi, A. (2003). Acceptance sampling based on truncated life tests in the Pareto distribution of the second kind. Advances and Applications of Statistics, 3(1), 33-48. |
| [5] | Balakrishnan, N., Leiva, V., Lopez, J. (2007). Acceptance sampling plans from truncated life tests based on the generalized Birnbaum-Saunders distribution. Communications in Statistics-Simulation and Computation, 36, 643-656. |
| [6] | Tsai, T.-R., Wu, S.-J. (2006). Acceptance sampling based on truncated life tests for generalized Rayleigh distribution. Journal of Applied Statistics, 33, 595-600. |
| [7] | Aslam, M. and Jun, C.-H. (2010). A double acceptance sam-pling plan for generalized log-logistic distributions with known shape parameters. Journal of Applied Statistics, 37(3), 405-414. |
| [8] | Jun, C.-H., Balamurali, S., and Lee, S.-H., 2006. Variables sampling plans for Weibull distributed lifetimes under sudden death testing. IEEE Transactions on Reliability, 55, 53-58. |
| [9] | Aslam, M. and Jun, C.-H. (2009). A group acceptance sam-pling plan for truncated life test having Weibull distribution. Journal of Applied Statistics, 36(9), 1021-1027 |
| [10] | Aslam, M., Jun, C.-H., Lee, H., Ahmad, M., and Rasool, M. (2011). Improved group sampling plans based on truncated life tests, The Chilean Journal of Statistics, 2 (1), 85-97. |
| [11] | Lio, Y.L., Tsai, T.-R. and Wu, S.-J. (2010a). Acceptance sampling plan based on the truncated life test in the Birnbaum Saunders distribution for percentiles. Communications in Statistics-Simulation and Computation, 39, pp.119-136. |
| [12] | Lio, Y.L., Tsai, T.-R. and Wu, S.-J. (2010b). Acceptance sampling plan for truncated life test based on the Burr Type XII percentiles. Journal of Chinese Institute of Industrial Engineers, 27(4), pp.270-280. |
| [13] | Marshall, A. W., Olkin, I. (2007). Life Distributions-Structure of Nonparametric, Semiparametric, and Parametric Families, New York: Springer. |
| [14] | Aslam, M., Mahmood, Y., Lio, Y.L., Tsai, T-R and Khan, M.A. (2011). Double Acceptance Sampling Plans for Burr Type XII Distribution Percentiles under the Truncated Life Test. Accepted by Journal of the Operational Research Society; online publication 2 November 2011; doi:10.1057/jors.2011.112 |

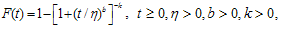 where
where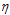 is the scale parameter,
is the scale parameter, 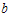 and
and 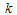 are the two shape parameters. When k=1, the burr type XII distribution converts to the log-logistic distribution. The 100
are the two shape parameters. When k=1, the burr type XII distribution converts to the log-logistic distribution. The 100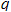 -th percentile of the burr type XII distribution is given as:
-th percentile of the burr type XII distribution is given as: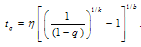 The rest of the paper is organized as follows, the design of the proposed plans and some of tables used for discussions are given in Section 2. Two applications in industrial are presented in Section 3. Section 4 compares the proposed two-stage sampling plan with sign stage sampling plan and concluding remarks are given at the end.
The rest of the paper is organized as follows, the design of the proposed plans and some of tables used for discussions are given in Section 2. Two applications in industrial are presented in Section 3. Section 4 compares the proposed two-stage sampling plan with sign stage sampling plan and concluding remarks are given at the end.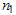 from a lot, allocate
from a lot, allocate 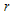 items to each of
items to each of 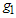 groups (or testers) so that
groups (or testers) so that 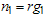 and put them on test for the duration of
and put them on test for the duration of 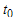 units of time. Accept the lot if the total number of failures from
units of time. Accept the lot if the total number of failures from 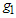 groups is smaller than or equal to
groups is smaller than or equal to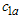 . Truncate the test and reject the lot as soon as the total number of failures is larger than or equal to
. Truncate the test and reject the lot as soon as the total number of failures is larger than or equal to 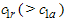 during the
during the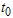 units of time. Otherwise, go to the second stage.2. (Second stage) Draw the second random sample of size
units of time. Otherwise, go to the second stage.2. (Second stage) Draw the second random sample of size 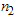 from the lot, allocate
from the lot, allocate 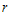 items to each of
items to each of 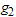 groups so that
groups so that 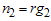 and put them on test for the duration of
and put them on test for the duration of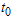 units of time again. Accept the lot if the total number of failures from
units of time again. Accept the lot if the total number of failures from 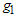 and
and 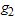 groups is smaller than or equal to
groups is smaller than or equal to 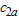 (>
(>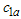 ). Otherwise, truncate the test and reject the lot.The proposed double group sampling plan is characterized by five design parameters, namely,
). Otherwise, truncate the test and reject the lot.The proposed double group sampling plan is characterized by five design parameters, namely, 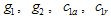 and
and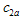 .It should be noticed that the proposed group sampling plan is different from the double acceptance sampling plans studied by Aslam et al.[14]. When
.It should be noticed that the proposed group sampling plan is different from the double acceptance sampling plans studied by Aslam et al.[14]. When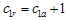 , the total number of failures from
, the total number of failures from 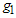 groups (denoted by
groups (denoted by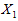 ) follows a binomial distribution with parameters
) follows a binomial distribution with parameters 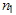 and
and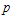 . Therefore, the lot acceptance probability at the first stage under the proposed double sampling plan is given by Aslam et al.[10].
. Therefore, the lot acceptance probability at the first stage under the proposed double sampling plan is given by Aslam et al.[10].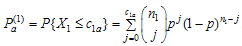
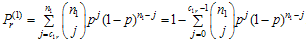
 and
and  groups (denoted by
groups (denoted by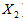 ) is smaller than or equal to
) is smaller than or equal to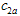 . Hence according to Aslam et al.[10],
. Hence according to Aslam et al.[10],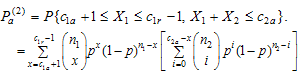
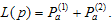
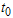 as a multiple of the specified percentile
as a multiple of the specified percentile 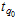 such that
such that 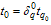 for a constant
for a constant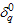 . For example
. For example 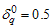 means that the experiment time is just half of the specified life percentile. The
means that the experiment time is just half of the specified life percentile. The 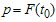 in terms of the 100q-th percentile of the Burr type XII distribution can be presented aswhere
in terms of the 100q-th percentile of the Burr type XII distribution can be presented aswhere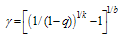
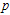 in terms of the median life is represented as
in terms of the median life is represented as 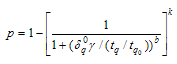
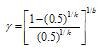
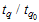 between the true percentile
between the true percentile 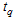 and targeted percentile
and targeted percentile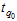 , the two-point approach of finding the design parameters is to determine the minimum number of groups,
, the two-point approach of finding the design parameters is to determine the minimum number of groups, 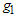 and
and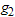 , and acceptance numbers,
, and acceptance numbers, 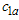 ,
, 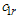 and
and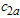 , to satisfy the following two inequalities
, to satisfy the following two inequalities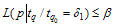
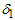 is the percentile ratio at the consumer’s risk and
is the percentile ratio at the consumer’s risk and 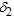 is the percentile ratio at the producer’s risk. Let
is the percentile ratio at the producer’s risk. Let 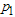 and
and 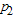 are the failure probabilities of corresponding to consumer’srisk and producer’s risk, respectively. The ASN under LTRL,
are the failure probabilities of corresponding to consumer’srisk and producer’s risk, respectively. The ASN under LTRL, 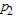 , is given by
, is given by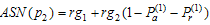
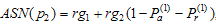
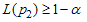
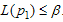
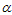 and
and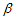 , the percentile ratio,
, the percentile ratio, 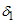 , at the consumer’s risk and the percentile ratio,
, at the consumer’s risk and the percentile ratio, 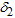 , at the producer’s risk, the design parameters of the proposed plan are determined such that the
, at the producer’s risk, the design parameters of the proposed plan are determined such that the 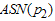 is minimized and inequalities (12b) and (12c) are satisfied simultaneously for specified values of shape parameters,
is minimized and inequalities (12b) and (12c) are satisfied simultaneously for specified values of shape parameters, 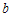 and
and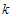 , termination ratio
, termination ratio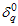 and the number of testers,
and the number of testers, 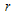 .If the shape parameters,
.If the shape parameters, 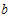 and
and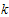 , are unknown, then the previous data information could be used to estimate these parameters.
, are unknown, then the previous data information could be used to estimate these parameters.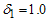 and
and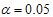 , the design parameters,
, the design parameters, 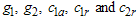 ,
, 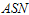 for the proposed plan as well as the probability of acceptance of the product are obtained for the ten percentiles of many Burr type XII distributions under each combination of
for the proposed plan as well as the probability of acceptance of the product are obtained for the ten percentiles of many Burr type XII distributions under each combination of 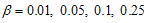 and
and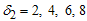 . Table 1 contains the results for the Burr type XII distribution with
. Table 1 contains the results for the Burr type XII distribution with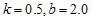 ; Table 2 has the results for the Burr type XII distribution with
; Table 2 has the results for the Burr type XII distribution with 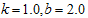 which is also called log-logistic distribution; Table 3 shows the results for the Burr type XII distribution with
which is also called log-logistic distribution; Table 3 shows the results for the Burr type XII distribution with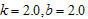 ; Table 4 displays the results for the Burr type XII distribution with
; Table 4 displays the results for the Burr type XII distribution with 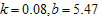 and the results for the Burr type XII distribution with
and the results for the Burr type XII distribution with 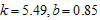 are placed in Table 5.From Tables 1-5, it can be noticed the following important trends in the design parameters and
are placed in Table 5.From Tables 1-5, it can be noticed the following important trends in the design parameters and
 in each table, all the design parameters and
in each table, all the design parameters and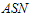 are non-increasing with respect to the percentile ratio
are non-increasing with respect to the percentile ratio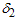 2. When the group size increases from 5 to 10, the numbers of groups for both stages are generally decreased for a given β and the percentile ratio
2. When the group size increases from 5 to 10, the numbers of groups for both stages are generally decreased for a given β and the percentile ratio 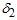 3. When the group size increases from 5 to 10,
3. When the group size increases from 5 to 10, 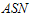 generally non-decreases for a given β and the percentile ratio
generally non-decreases for a given β and the percentile ratio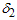 .4. When β increases, the numbers of groups for both stages are generally decreased for given group size
.4. When β increases, the numbers of groups for both stages are generally decreased for given group size 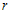 and the percentile ratio
and the percentile ratio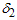 .
.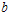 =5.47. Suppose that an experimenter would like to use the proposed two-stage sampling plan to establish the true unknown 10th percentile lifetime for the product is at least 4 months and experiment will be stopped after 4 months. Further, suppose that in the laboratory the experimenter has facility to install five items on a tester. This information leads to
=5.47. Suppose that an experimenter would like to use the proposed two-stage sampling plan to establish the true unknown 10th percentile lifetime for the product is at least 4 months and experiment will be stopped after 4 months. Further, suppose that in the laboratory the experimenter has facility to install five items on a tester. This information leads to 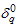 =1.0. Let β =0.01 and
=1.0. Let β =0.01 and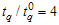 with
with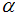 =0.05 for this experiment. Then from Table 4, the plan parameters are
=0.05 for this experiment. Then from Table 4, the plan parameters are 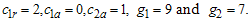 The two-stage acceptance sampling plan is implemented as follows: randomly select 45 items and distribute five items into each tester and accept the product if no failure is recorded in 4 months and reject the product if more than 1 failure is recorded before 4 months; otherwise, randomly select another 35 items from the lot and distribute five items into each tester. If the total number of failure items from the two-stage testing within four months for each stage is less than 2 then the lot is accepted; otherwise, the lot is rejected. According to this two-stage sampling plan, the experiment must be repeated when the number of failure is 1 from the first-stage test for four months. The probability of acceptance for this plan is 99.99% and
The two-stage acceptance sampling plan is implemented as follows: randomly select 45 items and distribute five items into each tester and accept the product if no failure is recorded in 4 months and reject the product if more than 1 failure is recorded before 4 months; otherwise, randomly select another 35 items from the lot and distribute five items into each tester. If the total number of failure items from the two-stage testing within four months for each stage is less than 2 then the lot is accepted; otherwise, the lot is rejected. According to this two-stage sampling plan, the experiment must be repeated when the number of failure is 1 from the first-stage test for four months. The probability of acceptance for this plan is 99.99% and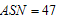 .Example-2Lio et al.[12] showed that the lifetime of oil breakdown of an insulating fluid under hightest voltage follows the Burr type XII distribution with k =5.49 and
.Example-2Lio et al.[12] showed that the lifetime of oil breakdown of an insulating fluid under hightest voltage follows the Burr type XII distribution with k =5.49 and 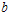 =0.85. Suppose that an experimenter would like to use the proposed two-stage sampling plan to establish the true unknown 10th percentile lifetime for the product is at least 6 months and experiment will be stopped after 6 months. Further suppose that the in laboratory the experimenter has facility to install ten items on a single tester. This information leads to
=0.85. Suppose that an experimenter would like to use the proposed two-stage sampling plan to establish the true unknown 10th percentile lifetime for the product is at least 6 months and experiment will be stopped after 6 months. Further suppose that the in laboratory the experimenter has facility to install ten items on a single tester. This information leads to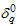 =1.0. Let β=0.05 and
=1.0. Let β=0.05 and 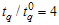 with
with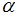 =0.05 for this experiment. Then from Table 5 with
=0.05 for this experiment. Then from Table 5 with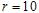 , the two-stage acceptance sampling plan parameters are
, the two-stage acceptance sampling plan parameters are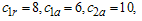
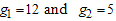 The sampling plan is implemented as follows: randomly select 120 items and distribute into ten testers such that tenitems on a single tester. Accept the product lot if less than seven failure items are recorded in 6 months and reject the product if more than 7 failures is recorded before 6 months. Otherwise, randomly select another 50 items and distribute into five testers evenly and test for 6 months. If the total number of failures from both stages is less than 11, then the lot is accepted; otherwise, the lot is rejected. From Table 5, the probability of acceptance is 95.58% and ASN =122 for this plan.
The sampling plan is implemented as follows: randomly select 120 items and distribute into ten testers such that tenitems on a single tester. Accept the product lot if less than seven failure items are recorded in 6 months and reject the product if more than 7 failures is recorded before 6 months. Otherwise, randomly select another 50 items and distribute into five testers evenly and test for 6 months. If the total number of failures from both stages is less than 11, then the lot is accepted; otherwise, the lot is rejected. From Table 5, the probability of acceptance is 95.58% and ASN =122 for this plan.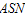 for the two-stage sampling plan. To save space, only the comparison for the Burr type XII with parameters
for the two-stage sampling plan. To save space, only the comparison for the Burr type XII with parameters 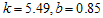 is displayed in this section. Table 6 shows the minimum number of groups and acceptance number for the total number of failures and
is displayed in this section. Table 6 shows the minimum number of groups and acceptance number for the total number of failures and 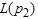 for single stage acceptance sampling plan. It could be noticed from Table 5 and Table 6, the proposed two-stage sampling plan generally has
for single stage acceptance sampling plan. It could be noticed from Table 5 and Table 6, the proposed two-stage sampling plan generally has 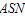 less than the sample size needed for a single sampling plan under the given rest conditions in both Tables 5 and 6.
less than the sample size needed for a single sampling plan under the given rest conditions in both Tables 5 and 6. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML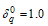

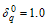

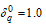

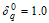 .
.