1. Introduction

The gravitational potential at a point in a gravitational field is measured by the amount of work done in bringing a unit mass from infinity to that point. The gradient of the potential gives the intensity of field at that point. With this knowledge of gravitational potential one can find the gravitational field strength at a point due to a body. In fact “The knowledge of the gravitational potential due to heavenly bodies helps us in understanding the dynamics of cluster of galaxies and gravitational bending of light due to galaxies of various shapes.” Notwithstanding “The Newton’s Law of Gravitation and Einstein’s Theory of Relativity” play an important role towards such developments in gravitational and relativistic theories. The Newtonian mechanics is applicable to macroscopic bodies, which are traveling with velocity much less than that of light. When the velocity of a body is comparable to that of light, the Newtonian mechanics fails. To eliminate this limitation of Newtonian mechanics, Einstein in 1905 proposed the special theory of relativity which can explain the motion of a particle moving with a velocity (v); where v is approximately equal to c (velocity of light) as well as << c. However, the special theory of relativity is applicable to inertial frames only and cannot be applicable to non-inertial or accelerated frame of reference. Einstein in 1915 ([8]) developed a theory of relativity that explains both accelerated and non-accelerated motion. According to Einstein, the effects of a gravitational field is precisely the same as those due to uniformly accelerated frame of reference provided acceleration of the frame is equal and opposite to the acceleration that gravitational field would impart to a particle in its frame. This principle is known as “Principle of Equivalence”. The theory of gravitational field formulated on the basis of the theory of relativity is called the “General Theory of Relativity”. Taking into consideration the four dimensional space times and using the solution of vacuum Einstein’s equation yield the motion of photon in a gravitational field. This is equivalent to the motion of the photon in medium with equivalent refractive index

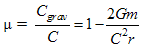Thus we find that the gravitational field behaves as a refracting medium having refractive index different from 1. So, a photon in a gravitational field behaves as if photon in an optical medium having a refractive index given by the above expression.

The theory of relativity developed by Einstein (1915[8]) explains both motion of accelerated and non-accelerated body based on the strong equivalence principle. Later he developed a mathematical theory relating gravitation with space-time interval (ds) between two points of an event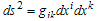, where 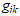is the metric tensor, whose values depend on the gravitational field. Einstein’s General Theory of relativity was able to explain the perihelion shift of mercury and the deflection of star light, which was not possible with the help of Newton’s theory of motion and gravitation. The experimental verification of light by Sun was performed by Eddington et. al. (1920) during the total solar eclipse of 1919. The other various experiments performed to test the general theory of relativity were solar gravitational deflection of radio waves, bending of microwave radiation in gravitational field of Sun, dual frequency measurement of the solar gravitational microwave deflection, verification of signal retardation by solar gravity, verification of the principle of equivalence from lunar laser ranging. Similarly, the path of light changes due to the gravitational field of galaxies.

Thus, the knowledge of the gravitational potential due to heavenly bodies is an important physical entity and this will help in understanding the gravitational bending of light due to galaxies of various shapes.

The gravitational potential at a point in a Gravitational Field is given by 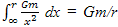.The gravitational potential of uniform circular disc of radius a and thickness t, density ρ at a point P on the axis at a distance r from the center of the disc (Chatterjee and Sengupta 2001[6]; Gamaw and Cleveland 1968 [11]) is given by

V = 2GM{r – (r²+a²)^1/2}/ a², where M = mass of the disc = πa² ρ t.

Similarly the gravitational potential of a thin uniform straight rod at any point P (Chatterjee and Sengupta[6]; Gamaw and Cleveland[11]) is given by

V = − Gm log{(r₁+r₂+l)/(r₁+r₂-l)}/lwhere m = mass of the rod, l = length of the rod, r₁ = distance of P from one end of the rod and r₁ = distance of P from the other end of the rod.

2. Objective

It may be noted here that all the calculations on gravitation potential at points outside non-spherical masses like disc or cylinder, available in existing literature, are done considering the points to be either on the axis or on the plane of the disc / cylinder. However we calculate the gravitational potential of uniform ellipsoidal mass at any point outside the body, which will be more general in nature. Our aim in this paper is to calculate the gravitational potential of an ellipsoidal mass of prolate shape at any point outside it.

3. Methods and Calculations

For the calculation of gravitational potential of an ellipsoidal mass of prolate shape at any point outside it we use the standard method of integration.

Let us consider a prolate of length 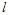(Fig 1). The gravitational potential at a point 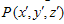is to be calculated. At first we calculate the gravitational potential due to the elementary disc at a distance z from the centre of the prolate and then it will be integrated for the whole length of the prolate for getting the total potential due to the whole prolate.

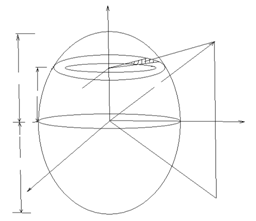Figure 1. Prolate shaped mass

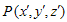We take spherical polar co-ordinate system. Let be the point, where potential is to be calculated, then we have

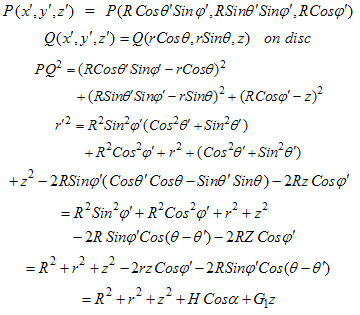where,

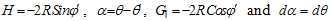The potential at p is obtained by

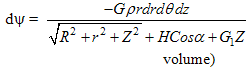(ρ density per unit volume)

where,

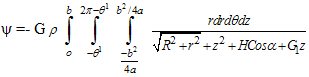(1)

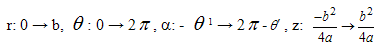
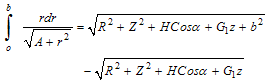(2)

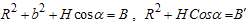Letting, we get

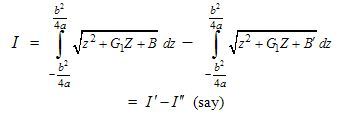(3)

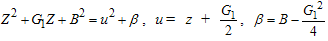
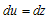Now, and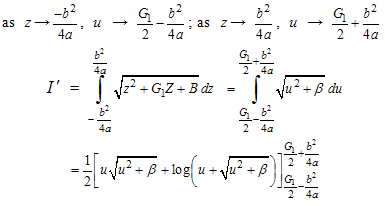

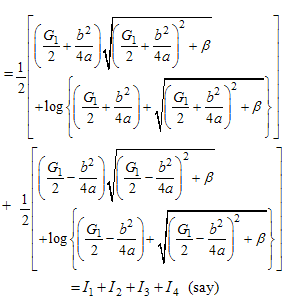where, ,

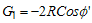and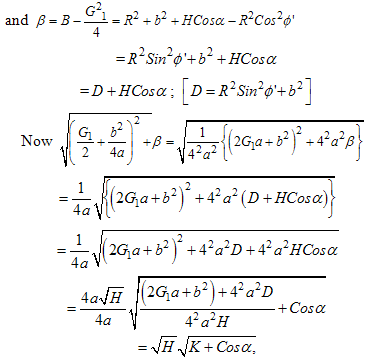

where,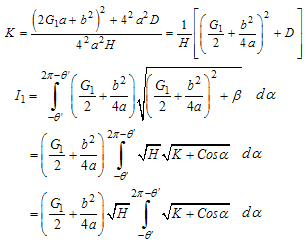

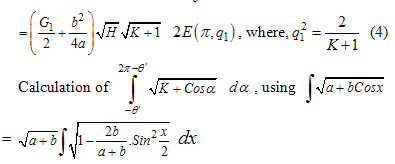we get,

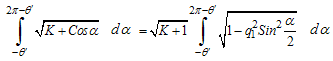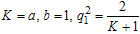where and 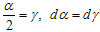considering x in the direction of P,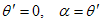

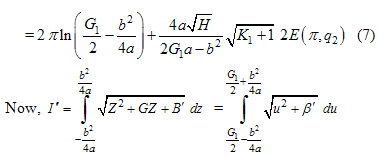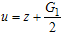where and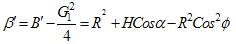

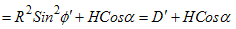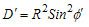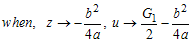where, and

and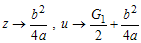

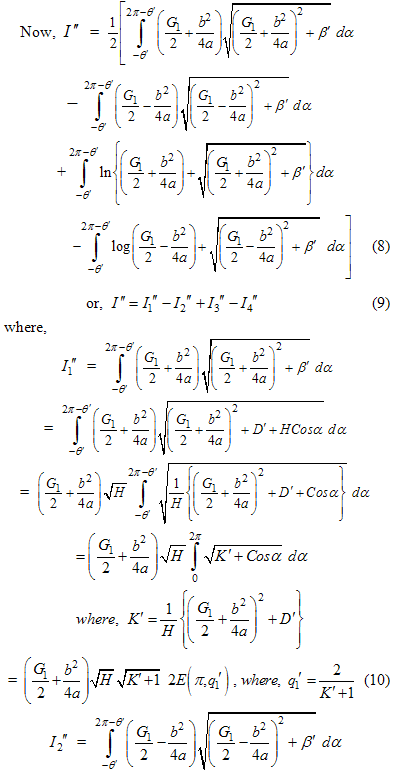
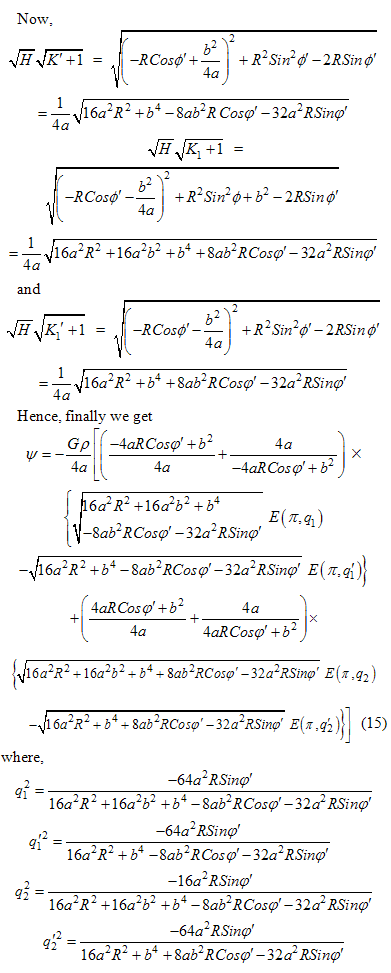
4. Results and Discussion

Thus, equation (15), calculated above, gives the expression for gravitational potential of an elliptical mass of prolate shape at any point outside the prolate. We know that in case of the calculation of gravitational potential of thin uniform straight rod at any point, if we draw an ellipse with A and B as foci then for all points on the ellipse, the sum of the focal distances will be the same (where for the point P on the surface of the ellipse the sum of the focal distances is (r₁ + r₂)) and for all points over the surface of the ellipse the potential is constant. The potential is also constant over the ellipsoid obtained by revolving this ellipse about the line joining the foci, i.e., about the line AB.

In figure 2, ψ vs R is plotted; φ =30⁰,45⁰ and 90⁰, figure 3 shows the plot of ψ vs φ. These figures show the variation of the Gravitational Potential with respect to angle φ and distance R (using FORTRAN – LF9556 Compiler). In Figure 3, we see that the value of ψ drops to a minimum and then rises again. This may be because of the fact that the potential remains constant only in some ellipsoidal surface like in case of a uniform rod as discussed above, whereas in this case the distance R is kept constant and it will generate a spherical surface.

Thus we find that the expression for gravitational potential of an elliptical mass of prolate shape at any point outside the prolate (equation (15)) is correct.

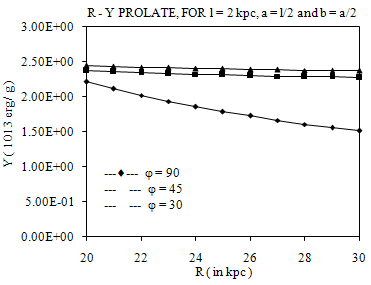Figure 2. Plot of Ψ (1013 erg / g ) and R ( in kpc ) for Prolate

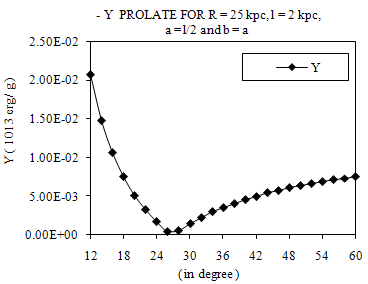Figure 3. Plot of Ψ (1013 erg / g ) and φ ( in degree ) for Prolate

5. Conclusions

The two graphs show that the gravitational potential decreases with the increase in distance and it takes the minimum value when φ is at 27.5 degrees.