Atul Tyagi 1, Dhirendra Chhajed 2
1Department of Mathematics & Statistics, University College of Science, Mohan Lal Sukhadia University, Udaipur, 313001, India
2Department of Mathematics, Sir Padampat Singhania University, Udaipur, 313601, India
Correspondence to: Atul Tyagi , Department of Mathematics & Statistics, University College of Science, Mohan Lal Sukhadia University, Udaipur, 313001, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
We have investigated homogeneous anisotropic Bianchi type IX cosmological model for perfect fluid distribution with electro-magnetic field. The magnetic field is due to an electric current produced along x axis thus is the only non-vanishing component of electromagnetic field tensor. To get a determinate model, we have assumed the condition between metric potentials, where is constant. The various physical and geometrical aspects of the model viz pressure, density, shear, expansion factor, electromagnetic field tensor and conformal curvature are also discussed.
Keywords:
Bianchi type IX, Cosmological Model, Anisotropic, Perfect Fluid, Electromagnetic Field
1 Introduction
Many relativists have taken keen interest in studying Bianchi IX universe because familiar solution like Robertson Walker universe, the de-sitter universe. The Taub-NUT solutions etc. are of Bianchi IX space times. Bianchi IX cosmological models include closed FRW models. These models allow not only expansion but also rotation and shear and in general are anisotropic. In recent years cosmological models with rotation and expansion have been constructed by many research workers viz. Novello and Reboucas[1] , Reboucas and Lima[2,3] , Rosquist[4], Bradley and Svienstins[5] , Svienstins[6], Patel and Yadava[7]. Homogeneous and anisotropic cosmological models have been widely studied in the frame work of general relativity in the search of realistic picture of the universe in its early stages because they explain a number of observed phenomena quite satisfactorily. The observational relations for discrete sources in certain homogeneous anisotropic model have been derived by Saunders[8, 9], Tomita[10], Mac-Callum and Ellis[11]. Ftaclas & Cohen[12] have investigated LRS (Locally Rotationally Symmetric) Bianchi type V universes containing stiff matter with electromagnetic field. Lorentz[13,14 ] investigated Bianchi type cosmologies in presence of magnetic field. Assad and Soares[15] have investigated a class of exact cosmological solution of Einstein’s – Maxwell equations, which are anisotropic and spatially homogeneous. Bianchi VIII and IX locally rotationally symmetric model.The dynamical effects of spatially homogeneous electromagnetic field on anisotropic Bianchi type IX models are studied by Waller[16]. Brill[17] studied Einstein’s - Maxwell equations in a homogeneous and non-isotropic universe. Bali and Dave[18] have investigated Bianchi type IX string cosmological model in General Relativity. Bali and Kumawat[19] have investigated Bianchi type IX stiff fluid tilted cosmological model with bulk viscosity. Tyagi and Sharma[20] investigated Bianchi IX string cosmological model for perfect fluid distribution in General Relativity.In this paper, we have investigated homogeneous anisotropic Bianchi type IX cosmological model of perfect fluid distribution with electro-magnetic field. We have assumed that 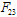 is the only non-vanishing component of electromagnetic field tensor
is the only non-vanishing component of electromagnetic field tensor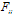 .To get a determinate model, we have assumed the condition
.To get a determinate model, we have assumed the condition 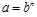 between metric potentials, where n is constant. The various physical and geometrical aspects of the model are also discussed.
between metric potentials, where n is constant. The various physical and geometrical aspects of the model are also discussed.
2. Formations of Field Equations
We consider homogeneous anisotropic Bianchi type IX metric in the form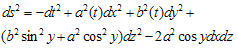 | (1) |
Where metric potentials 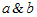 are functions of ‘t’ alone.The energy momentum tensor is taken in the form
are functions of ‘t’ alone.The energy momentum tensor is taken in the form 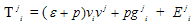 | (2) |
p being the pressure, 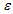 the density.The co-ordinates are considered to be comoving so that
the density.The co-ordinates are considered to be comoving so that 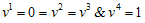 for the line element (1)The electromagnetic field
for the line element (1)The electromagnetic field 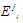 is defined by
is defined by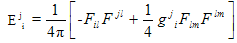 | (3) |
Maxwell’s equation 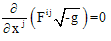 | (4) |
Equation (4) leads to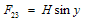 | (5) |
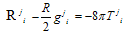 for the line element (1) are given by
for the line element (1) are given by 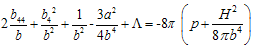 | (6) |
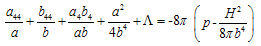 | (7) |
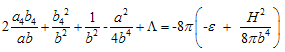 | (8) |
3. Solutions of the Field Equations
Equations (6) - (8) are three equations in four unknown 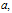
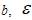 and
and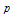 . To get a determinate solution, we assume the condition between metric potentials
. To get a determinate solution, we assume the condition between metric potentials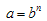 | (9) |
Equation (6) and (7) together lead to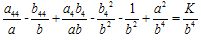 | (10) |
Where 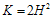 Using the condition (9) in (10), we get
Using the condition (9) in (10), we get 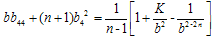 | (11) |
Putting 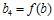 in equation (11), we get
in equation (11), we get 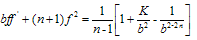 | (12) |
Equation (12) leads to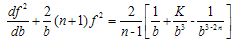 | (13) |
Equation (13) leads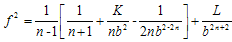 | (14) |
Where L is constant of integration. (14)Equation (14) leads to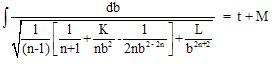 | (15) |
Where M is constant of integration, value of b can be determined from equationThe metric (1) reduces to form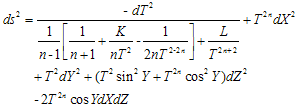 | (16) |
Where 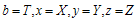
4. Some physical and Geometrical Features
Pressure and density for the model (16) are given by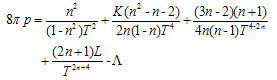 | (17) |
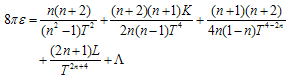 | (18) |
The condition 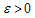 leads to
leads to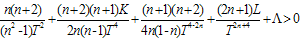 Condition
Condition 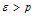 leads to
leads to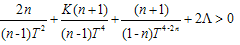 Which is condition on
Which is condition on  The charge current vector
The charge current vector 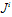 is given by
is given by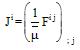 This turns out to be zero.The scalar of expansion
This turns out to be zero.The scalar of expansion 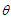 calculated for the flow vector
calculated for the flow vector 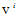 is given by
is given by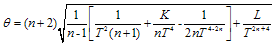 | (19) |
The rotation 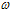 is identically zero. The non-vanishing components of Shear
is identically zero. The non-vanishing components of Shear 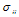 are given by
are given by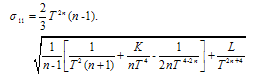 | (20) |
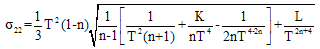 | (21) |
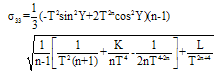 | (22) |
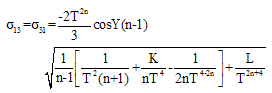 | (23) |
Hence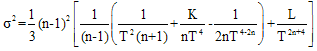 | (24) |
The non-vanishing components of conformal curvature tensor are given by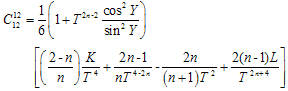 | (25) |
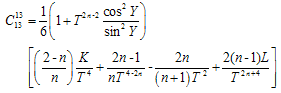 | (26) |
 | (27) |
5. Conclusions
The expansion in the model decreases as time increases. The expansion stop at T=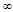 and also when
and also when 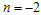 since
since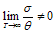 , therefore, the model doesn’t approach isotropy for large value of T. However when n = 1 the model is isotropize. When
, therefore, the model doesn’t approach isotropy for large value of T. However when n = 1 the model is isotropize. When 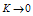 then
then 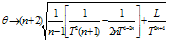 which show that the expansion in the model tend to zero for large value of T in the absence of magnetic field. The space-time is petrov type-D. In general, the model represent expanding, shearing and non- rotating universe.
which show that the expansion in the model tend to zero for large value of T in the absence of magnetic field. The space-time is petrov type-D. In general, the model represent expanding, shearing and non- rotating universe.
References
| [1] | Novello, M & Reboucas, M.J. (1978) Astrophys, J 225, 719 |
| [2] | Reboucas, M.J. and Lima, J.A.S. (1982) J. Maths. Phys. 23, 1547 |
| [3] | Reboucas, M.J. and Lima, J.A.S. (1982) J. Maths. Phys. 29 , 2699 |
| [4] | Rosquist, K (1983) phys .97 A, 145 |
| [5] | Bradely M. and Svienstins , E.(1983) Gen. Relativity Gravitation 16, 1119 |
| [6] | Svienstins, E.(1985) ) Gen. Relativity Gravitation. 17, 54 |
| [7] | Patel, L.K. and Yadav S.P.(1987) Indian J. of pure & applied Math. 18(9), 840-845 |
| [8] | P.T. Saunder, Observations in homogeneous model universes. Mon. Not. R.. Astr. Soc. 141, (1968), 427-437. |
| [9] | P.T. Saunder, Observations in some simple cosmological Models with shear. (1969)Mon. Not. R. astro. Soc. 142, 213-227. |
| [10] | K. Tomita, Theoretical relations among observable quantities in an anisotropic & Homogeneous Universe. Progress. theoretical phys. (1968) 40, 2, 264-276 |
| [11] | M.A.H. Mac Callum & G.F.R. Ellis, A class of homogeneous cosmological models II: observations (1970) Comm. Math. Phys. 19, 1, 31-64. |
| [12] | C. Ftaclas, & J.M. Cohen, LRS(Locally Rotationally Symmetric) Bianchi type V universes containing stiff matter with electromagnetic field, (1978)Phys. Rev D 18 4373 . |
| [13] | D. Lorentz, An exact Bianchi type V tilted cosmological Model with matter & an Electromagnetic field,(1981) G.R.G. 13, 8, 795-805. |
| [14] | D. Lorentz, Exact Bianchi type cosmological models with matter & and electromagnetic field,(1982) Atrophy’s. & Space Science. 85, 1-2, 69-74. |
| [15] | M.J.D. Assad and I. Damio Soares , Anisotropic Bianchi types VIII & IX locally rotationally symmetric cosmologies , Phys. Rev D.28, 8, (1983), 1858-1865. |
| [16] | S.M.Waller, Bianchi type IX electromagnetic universes, (1984)P hys. Rev. D. 29, 2, 176-185. |
| [17] | D.R.Brill, Electromagnetic fields in a Homogeneous, Non isotropic universe. (1964) Phys, Rev. 133, 3B B845-B848. |
| [18] | Bali, R & Dave S. Bianchi type IX string cosmological model in General Relativity. Pramana J. of physics,(2001), 56,4 |
| [19] | Bali, R & Kumawat P Bianchi type IX stiff fluid tilted cosmological model with bulk viscosity(201 EJTP 7, No 24 , 383-394 |
| [20] | Tyagi,A & Sharma K Bianchi IX string cosmological model for perfect fluid distribution in General Relativity(2010) CHIN.PHYS.LETT. Vol 27, No 7079801 |

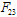 is the only non-vanishing component of electromagnetic field tensor
is the only non-vanishing component of electromagnetic field tensor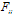 .To get a determinate model, we have assumed the condition
.To get a determinate model, we have assumed the condition 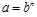 between metric potentials, where n is constant. The various physical and geometrical aspects of the model are also discussed.
between metric potentials, where n is constant. The various physical and geometrical aspects of the model are also discussed.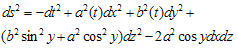
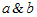 are functions of ‘t’ alone.The energy momentum tensor is taken in the form
are functions of ‘t’ alone.The energy momentum tensor is taken in the form 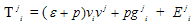
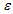 the density.The co-ordinates are considered to be comoving so that
the density.The co-ordinates are considered to be comoving so that 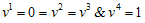 for the line element (1)The electromagnetic field
for the line element (1)The electromagnetic field 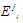 is defined by
is defined by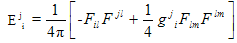
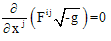
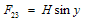
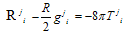 for the line element (1) are given by
for the line element (1) are given by 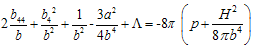
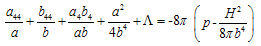
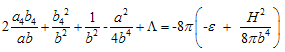
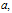
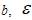 and
and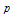 . To get a determinate solution, we assume the condition between metric potentials
. To get a determinate solution, we assume the condition between metric potentials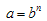
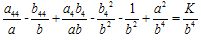
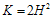 Using the condition (9) in (10), we get
Using the condition (9) in (10), we get 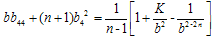
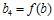 in equation (11), we get
in equation (11), we get 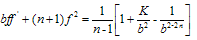
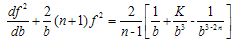
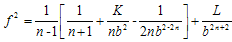
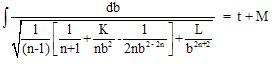
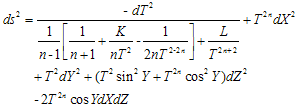
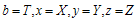
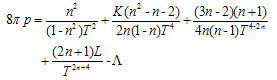
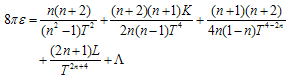
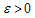 leads to
leads to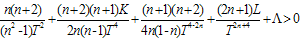 Condition
Condition 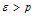 leads to
leads to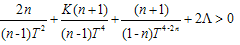 Which is condition on
Which is condition on  The charge current vector
The charge current vector 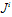 is given by
is given by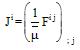 This turns out to be zero.The scalar of expansion
This turns out to be zero.The scalar of expansion 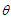 calculated for the flow vector
calculated for the flow vector 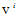 is given by
is given by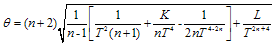
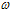 is identically zero. The non-vanishing components of Shear
is identically zero. The non-vanishing components of Shear 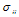 are given by
are given by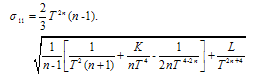
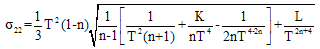
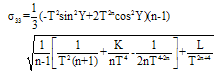
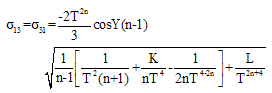
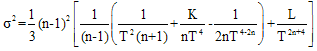
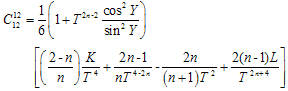
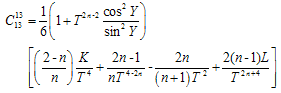

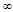 and also when
and also when 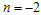 since
since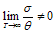 , therefore, the model doesn’t approach isotropy for large value of T. However when n = 1 the model is isotropize. When
, therefore, the model doesn’t approach isotropy for large value of T. However when n = 1 the model is isotropize. When 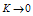 then
then 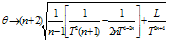 which show that the expansion in the model tend to zero for large value of T in the absence of magnetic field. The space-time is petrov type-D. In general, the model represent expanding, shearing and non- rotating universe.
which show that the expansion in the model tend to zero for large value of T in the absence of magnetic field. The space-time is petrov type-D. In general, the model represent expanding, shearing and non- rotating universe. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML