Manuel Alberto M. Ferreira, Marina Andrade
Department of Quantitative Methods, University Institute of Lisbon, Lisbon, 1649-026, Portugal
Correspondence to: Manuel Alberto M. Ferreira, Department of Quantitative Methods, University Institute of Lisbon, Lisbon, 1649-026, Portugal.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Solving a Riccati equation a collection of service times distributions, very general, is determined. For it the 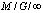 queue busy period and busy cycle probabilistic study, very comfortable, is performed. In addition the properties of that distributions collection are deduced and also presented.
queue busy period and busy cycle probabilistic study, very comfortable, is performed. In addition the properties of that distributions collection are deduced and also presented.
Keywords:
Riccati Equation, Probability Distributions, 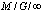 , Busy Period, Busy Cycle
, Busy Period, Busy Cycle
Cite this paper: Manuel Alberto M. Ferreira, Marina Andrade, Busy Period and Busy Cycle Distributions and Parameters for a Particular M/G/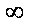 Queue System, American Journal of Mathematics and Statistics, Vol. 2 No. 2, 2012, pp. 10-15. doi: 10.5923/j.ajms.20120202.03.
Queue System, American Journal of Mathematics and Statistics, Vol. 2 No. 2, 2012, pp. 10-15. doi: 10.5923/j.ajms.20120202.03.
1. Introduction
In the 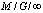 queue system the costumers arrive according to a Poisson process at rate
queue system the costumers arrive according to a Poisson process at rate 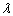 . They receive a service which length is a positive random variable with distribution function G(.) and mean
. They receive a service which length is a positive random variable with distribution function G(.) and mean 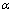 . There are always available servers. The traffic intensity is
. There are always available servers. The traffic intensity is 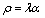 .At the operation of a
.At the operation of a 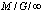 queue system, such as in any other queue system, there is a sequence of idle periods and busy periods. An idle period followed by a busy period is called a busy cycle.When applying this queue system to real problems, the busy period and the busy cycle length probabilistic study is very important. Along this work it is shown that the solution of the problem may be obtained solving a Riccati equation. The solution is a collection of service distributions for which both the busy period and the busy cycle have lengths with quite simple distributions, generally related with exponential distributions and the degenerated at the origin one.Some results for that collection of service distributions are also presented.
queue system, such as in any other queue system, there is a sequence of idle periods and busy periods. An idle period followed by a busy period is called a busy cycle.When applying this queue system to real problems, the busy period and the busy cycle length probabilistic study is very important. Along this work it is shown that the solution of the problem may be obtained solving a Riccati equation. The solution is a collection of service distributions for which both the busy period and the busy cycle have lengths with quite simple distributions, generally related with exponential distributions and the degenerated at the origin one.Some results for that collection of service distributions are also presented.
2. A Riccati Equation Important in the M/G/∞ Occupation Study
Defining 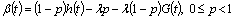 , where
, where 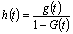 with
with 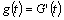 it is obtained
it is obtained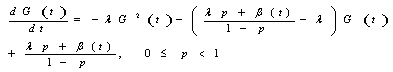 | (1) |
a Riccati equation which solution is 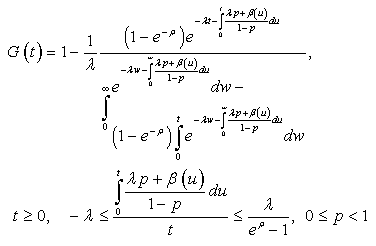 | (2) |
see [1]. Note that, for 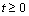 ,
, 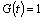 is a solution.
is a solution.
3. Busy Period and Busy Cycle Study
After (2) and considering  | (3) |
that is the 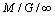 system busy period Laplace transform, see [2], it is obtained
system busy period Laplace transform, see [2], it is obtained 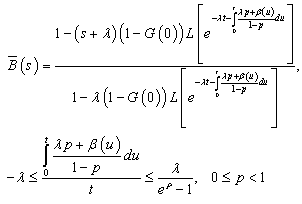 | (4) |
where 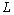 means Laplace transform and
means Laplace transform and 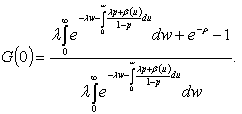 After expression (4) it is possible to compute
After expression (4) it is possible to compute  which inversion gives
which inversion gives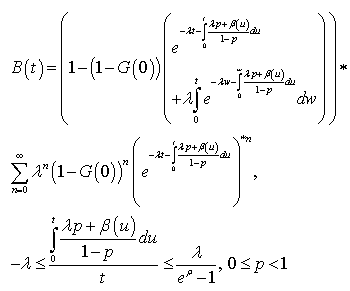 | (5) |
for the 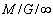 system busy period length distribution function, being
system busy period length distribution function, being  the convolution operator.If
the convolution operator.If 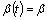 (constant), (2) becomes, see[3],
(constant), (2) becomes, see[3], 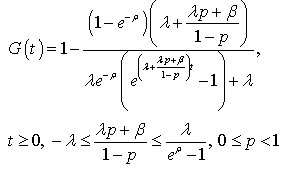 | (6) |
and (5) 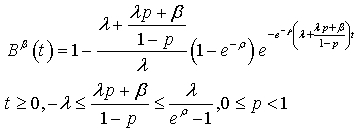 | (7) |
So, if the service distribution is given by (6), the busy period distribution function is the one of the mixture of a degenerated distribution at the origin with an exponential. For 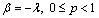 ,
,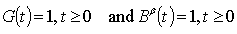 that is if the service distribution is degenerated at the origin with probability 1 it happens the same with the busy period distribution.Finally note that for
that is if the service distribution is degenerated at the origin with probability 1 it happens the same with the busy period distribution.Finally note that for 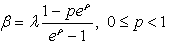
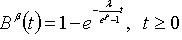 (purely exponential). And
(purely exponential). And 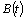 given by (5) satisfies
given by (5) satisfies 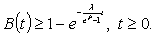 Calling
Calling 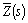 the busy cycle length Laplace transform, and noting that the
the busy cycle length Laplace transform, and noting that the 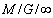 queue idle period is exponentially distributed with parameter
queue idle period is exponentially distributed with parameter 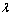 - as it happens for any queue system with Poisson arrivals at rate
- as it happens for any queue system with Poisson arrivals at rate 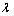 - and that the idle period and the busy period are independent for the
- and that the idle period and the busy period are independent for the 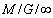 queue, see[4], it is obtained
queue, see[4], it is obtained 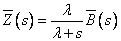 | (8) |
After (4) and (8) it is possible to compute 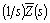 which inversion gives
which inversion gives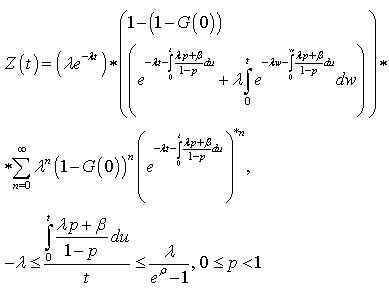 | (9) |
for the busy cycle distribution function. If 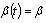 (constant) (9) becomes
(constant) (9) becomes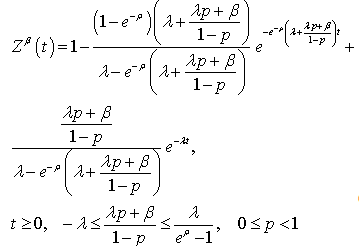 | (10) |
So, if the service time distribution function is given by (6) the busy cycle distribution function is the mixture of two exponential distributions.Note that, for 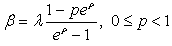
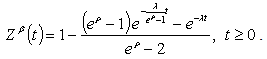 .And
.And 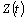 , given by (9), satisfies
, given by (9), satisfies 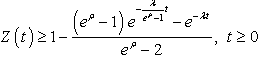 | (11) |
Note that (11) is coherent even for 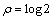 since
since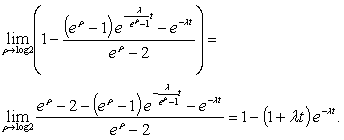 For
For 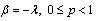
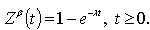 Finally, also for
Finally, also for 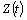 given by (9),
given by (9), 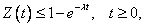 | (12) |
4. Busy Period and Busy Cycle Parameters
As for the busy period moments, calling B the busy period random variable, note that (3) is equivalent to, see [5], 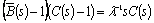 ,being
,being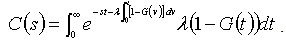 .Differentiating
.Differentiating 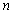 times, using Leibnitz’s formula and making
times, using Leibnitz’s formula and making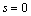 , results
, results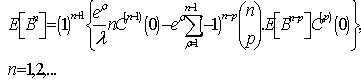 | (13) |
where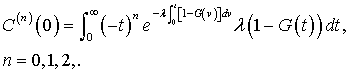 | (14) |
The expression (13) gives a recursive method to compute 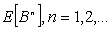 as a function of
as a function of 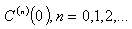 So it is possible to write exact expressions for the moments centred at the origin.Making
So it is possible to write exact expressions for the moments centred at the origin.Making 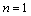 it is obtained
it is obtained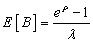 | (15) |
as it is well known, independently of the service time distribution.For the busy cycle moments, if Z is the busy cycle random variable, 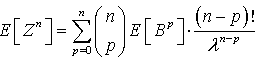 | (16) |
The M|G|∞ queue busy period “peak” is the Laplace transform value at 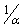 , see[6]. It is a parameter that characterizes the busy period distribution and contains information about all its moments. For the collection of service distributions (2) the “peak”, called
, see[6]. It is a parameter that characterizes the busy period distribution and contains information about all its moments. For the collection of service distributions (2) the “peak”, called 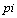 , is
, is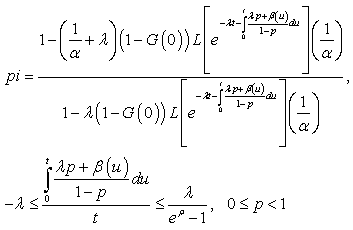 | (17) |
For 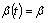 (constant), see[7],
(constant), see[7],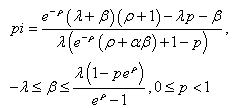 | (18) |
In[6] it is also introduced another measure: the “modified peak” got after the “peak” taking out the terms that are permanent for the busy period in different service distributions and putting over the common part. Call it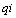 . It is easy to verify that
. It is easy to verify that 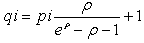 and, so, for the distributions given by collection (2) with
and, so, for the distributions given by collection (2) with 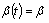 (constant), so collection (6), see again[7],
(constant), so collection (6), see again[7],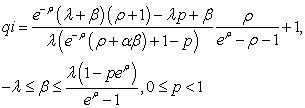 | (19) |
For the busy cycle of the M|G|∞ queue the “peak”, see[8], called now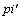 , for the service distributions given by the collection (2) is
, for the service distributions given by the collection (2) is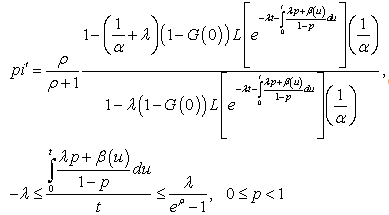 | (20) |
With 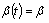 (constant), see[7],
(constant), see[7],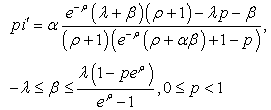 | (21) |
And the “modified peak”, called now 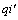 , given by
, given by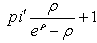 , for the service distributions given by the collection (6) is
, for the service distributions given by the collection (6) is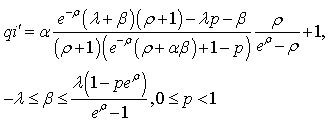 | (22) |
The busy cycle renewal function value of the M|G|∞ queue, at the instant 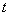 , gives the mean number of busy periods that begin in
, gives the mean number of busy periods that begin in 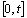 , see [9]. Calling it
, see [9]. Calling it 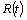 :
: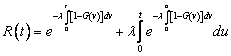 | (23) |
If the service time is a random variable with distribution function given by a member of the collection (6)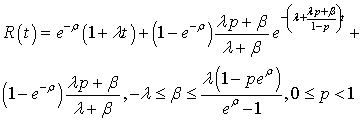 | (24) |
5. Collection (2) Distributions Moments Computation
If, in (2), 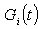 is the solution associated to
is the solution associated to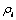 ,
, 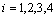 it is easy to see that
it is easy to see that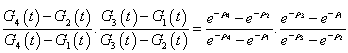 | (25) |
as it had to happen since the differential equation considered is a Riccati one.And computing,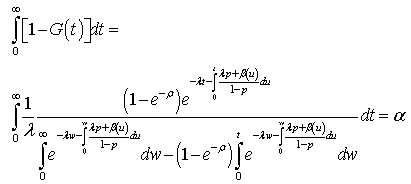 in accordance to the fact that (2) is a collection of positive random variables distribution functions.The density associated to
in accordance to the fact that (2) is a collection of positive random variables distribution functions.The density associated to 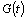 given by (2) is
given by (2) is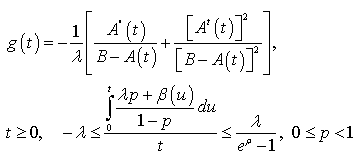 | (26) |
where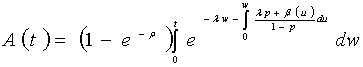 and
and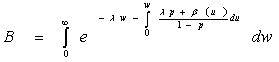 If
If 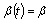 (constant), see[7],
(constant), see[7],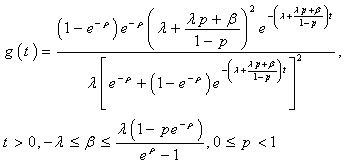 | (27) |
So,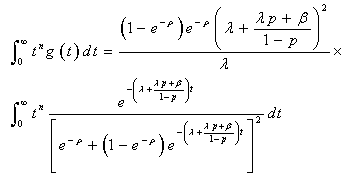 | (28) |
But, 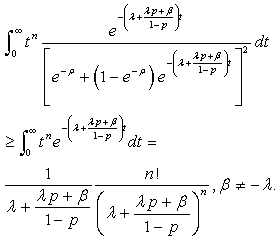 And,
And, 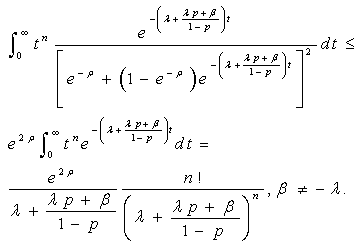 So, calling
So, calling 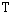 the random variable corresponding to:
the random variable corresponding to: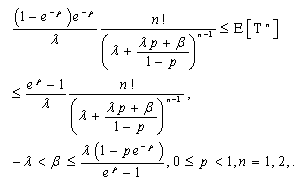 | (29) |
Notes:The expression (29), giving bounds for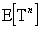 , guarantees its existence,For
, guarantees its existence,For 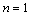 the expression (29) is useless because
the expression (29) is useless because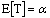 . Note, curiously, that the upper bound is
. Note, curiously, that the upper bound is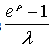 , the M/G/∞ system busy period mean value,For
, the M/G/∞ system busy period mean value,For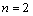 , subtracting to both bounds,
, subtracting to both bounds, 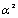 from expression (29) result bounds for
from expression (29) result bounds for 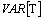 ,For
,For 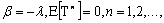 evidently.See, however, that (6) can be put like:
evidently.See, however, that (6) can be put like: 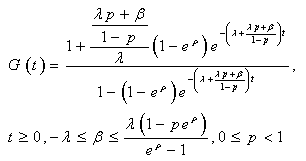 | (30) |
And, for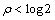 ,
,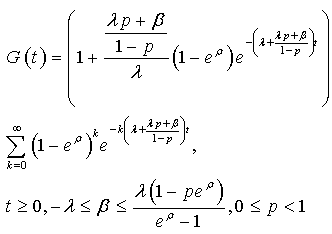 | (31) |
After (31) the Laplace Transform for 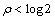 , can be easily derived. And, so, - For
, can be easily derived. And, so, - For 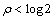
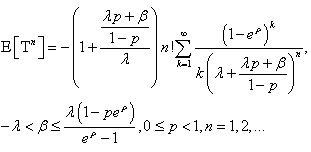 | (32) |
Notes: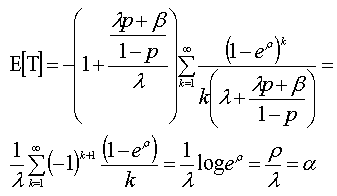 For
For  only a finite number of parcels in the infinite sum must be taken. Calling
only a finite number of parcels in the infinite sum must be taken. Calling  this number, to get an error lesser than
this number, to get an error lesser than 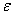 it is necessary to have simultaneously
it is necessary to have simultaneously 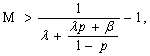
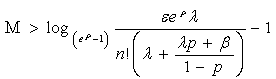 .So it is evident now that this distributions collection moments computation is a complex task. This was already true for the study of[10] where the results presented are a particular situation of these ones for
.So it is evident now that this distributions collection moments computation is a complex task. This was already true for the study of[10] where the results presented are a particular situation of these ones for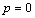 .The consideration of the approximation
.The consideration of the approximation 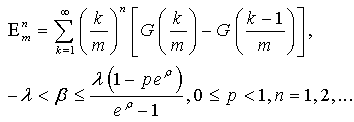 | (33) |
may be helpful since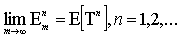 , see[11], that allow the numerical computation of the moments.
, see[11], that allow the numerical computation of the moments.
6. Conclusions
The function 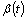 , defined in 1., that leads to the equation (1), the source of the results presented, is induced by the M/G/∞ transient probabilities monotony study, see[1] and[3]. Being well known the close relations existing among the transient behaviour and the busy period distributions, it is not surprising that the service distribution functions, solutions of (1), give rise to so friendly distributions to the M/G/∞ queue busy period. This is a quite unusual situation, that allows simple computations for the probabilities and parameters of the busy period and busy cycle.This so simple structure lies on the exponential distribution and the deterministic one. In many of the situations seen there are purely deterministic and exponential distributions, mixtures of deterministic and exponential distributions and mixtures of two exponential distributions. The great presence of the exponential distribution in this context is due certainly to the so friendly properties of the Poisson Process and to the structure of the function resulting from the inversion of the Laplace Transform given by (4).Even the stochastic processes related with this queue become quite simple. They are very close to the Poisson Process and in certain situations are even Poisson Processes.In conclusion, all of this results in a very simple expression for the inversion of (4), with the service distributions solutions of (1). In consequence, as it was shown in this work, the distribution functions and the parameters for the busy period and, consequently, for the busy cycle result very simple to compute and interpret.Many of these results are true for other service distribution functions, in the case of insensibility: parameters that depend on the service distribution only through its mean. Some others may result in good approximations.Note still that when the distribution functions for
, defined in 1., that leads to the equation (1), the source of the results presented, is induced by the M/G/∞ transient probabilities monotony study, see[1] and[3]. Being well known the close relations existing among the transient behaviour and the busy period distributions, it is not surprising that the service distribution functions, solutions of (1), give rise to so friendly distributions to the M/G/∞ queue busy period. This is a quite unusual situation, that allows simple computations for the probabilities and parameters of the busy period and busy cycle.This so simple structure lies on the exponential distribution and the deterministic one. In many of the situations seen there are purely deterministic and exponential distributions, mixtures of deterministic and exponential distributions and mixtures of two exponential distributions. The great presence of the exponential distribution in this context is due certainly to the so friendly properties of the Poisson Process and to the structure of the function resulting from the inversion of the Laplace Transform given by (4).Even the stochastic processes related with this queue become quite simple. They are very close to the Poisson Process and in certain situations are even Poisson Processes.In conclusion, all of this results in a very simple expression for the inversion of (4), with the service distributions solutions of (1). In consequence, as it was shown in this work, the distribution functions and the parameters for the busy period and, consequently, for the busy cycle result very simple to compute and interpret.Many of these results are true for other service distribution functions, in the case of insensibility: parameters that depend on the service distribution only through its mean. Some others may result in good approximations.Note still that when the distribution functions for 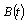 and
and 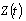 are a little more complicated, simple bounds are presented. In the field of Queuing Theory this situation seems unique, there having no news of anything similar.
are a little more complicated, simple bounds are presented. In the field of Queuing Theory this situation seems unique, there having no news of anything similar.
ACKNOWLEDGEMENTS
This work was financially supported by FCT through the Strategic Project PEst-OE/EGE/UI0315/2011.
References
| [1] | M. A. M. Ferreira and M. Andrade, 2011, queue system transient behavior with time origin at an operation beginning instant and occupation, Journal of Mathematics and Technology, 2(1), 54-60 |
| [2] | W. Stadje, 1985, The busy period of the queueing , Journal of Applied Probability, 22, 697-704 |
| [3] | M. A. M. Ferreira and M. Andrade, 2010, Looking to a system occupation through a Riccati equation, Journal of Mathematics and Technology, 1(2), 58-62 |
| [4] | L. Takács, An Introduction to Queueing Theory, Oxford University Press, 1962 |
| [5] | M. A. M. Ferreira, Comportamento transeunte e período de ocupação de sistemas de filas de espera sem espera, PhD thesis, ISCTE, Lisbon, Portugal, April 1995 |
| [6] | M. A. M. Ferreira, 1997, Um parâmetro caracterizador da distribuição do período de ocupação da fila de espera , Revista Portuguesa de Gestão II, 99-102 |
| [7] | M. A. M. Ferreira and M. Andrade, 2009, queue system parameters for a particular collection of service time distributions, African Journal of Mathematics and Computer Science Research, 2(7), 138-141 |
| [8] | M. A. M. Ferreira, 1999, Application of the “modified peak” to characterize the queue busy cycle length distribution, Statistical Review, 3(3), 47-56 |
| [9] | M. A. M. Ferreira, 2004, queue busy cycle renewal function for some particular service time distributions, Proceedings of Quantitative Methods in Economics (Multiple Criteria Decision Making XII), Virt. Slovakia |
| [10] | M. A. M. Ferreira, 1998, Momentos de Variáveis Aleatórias com Função de Distribuição dadas pela Colecção 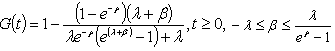 . Revista Portuguesa de Gestão, II, 67-69 . Revista Portuguesa de Gestão, II, 67-69 |
| [11] | M. A. M. Ferreira, Redes de Filas de Espera, Master Thesis, IST-UTL, Lisbon, Portugal, Feb 1987 |
| [12] | M. A. M. Ferreira and M. Andrade, 2011, Fundaments of theory of queues, International Journal of Academic Research, 3(1, Part II), 427-429 |
| [13] | M. A. M. Ferreira and M. Andrade, 2010 queue busy period tail, Journal of Mathematics and Technology, 1 (3), 11-16 |
| [14] | M. Andrade, 2010, A note on foundations of probability, Journal of Mathematics and Technology, 1 (1), 96-98 |
 Queue System
Queue System
 queue busy period and busy cycle probabilistic study, very comfortable, is performed. In addition the properties of that distributions collection are deduced and also presented.
queue busy period and busy cycle probabilistic study, very comfortable, is performed. In addition the properties of that distributions collection are deduced and also presented.
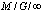 , Busy Period, Busy Cycle
, Busy Period, Busy Cycle
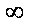 Queue System, American Journal of Mathematics and Statistics, Vol. 2 No. 2, 2012, pp. 10-15. doi: 10.5923/j.ajms.20120202.03.
Queue System, American Journal of Mathematics and Statistics, Vol. 2 No. 2, 2012, pp. 10-15. doi: 10.5923/j.ajms.20120202.03.
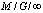 queue system the costumers arrive according to a Poisson process at rate
queue system the costumers arrive according to a Poisson process at rate 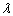 . They receive a service which length is a positive random variable with distribution function G(.) and mean
. They receive a service which length is a positive random variable with distribution function G(.) and mean 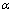 . There are always available servers. The traffic intensity is
. There are always available servers. The traffic intensity is 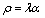 .At the operation of a
.At the operation of a 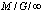 queue system, such as in any other queue system, there is a sequence of idle periods and busy periods. An idle period followed by a busy period is called a busy cycle.When applying this queue system to real problems, the busy period and the busy cycle length probabilistic study is very important. Along this work it is shown that the solution of the problem may be obtained solving a Riccati equation. The solution is a collection of service distributions for which both the busy period and the busy cycle have lengths with quite simple distributions, generally related with exponential distributions and the degenerated at the origin one.Some results for that collection of service distributions are also presented.
queue system, such as in any other queue system, there is a sequence of idle periods and busy periods. An idle period followed by a busy period is called a busy cycle.When applying this queue system to real problems, the busy period and the busy cycle length probabilistic study is very important. Along this work it is shown that the solution of the problem may be obtained solving a Riccati equation. The solution is a collection of service distributions for which both the busy period and the busy cycle have lengths with quite simple distributions, generally related with exponential distributions and the degenerated at the origin one.Some results for that collection of service distributions are also presented.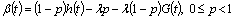 , where
, where 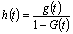 with
with 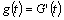 it is obtained
it is obtained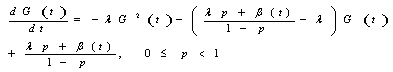
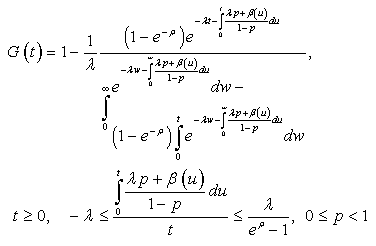
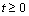 ,
, 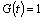 is a solution.
is a solution.
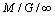 system busy period Laplace transform, see [2], it is obtained
system busy period Laplace transform, see [2], it is obtained 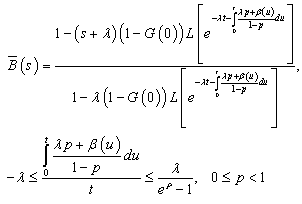
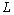 means Laplace transform and
means Laplace transform and 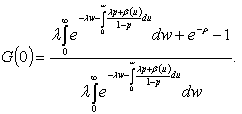 After expression (4) it is possible to compute
After expression (4) it is possible to compute 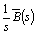 which inversion gives
which inversion gives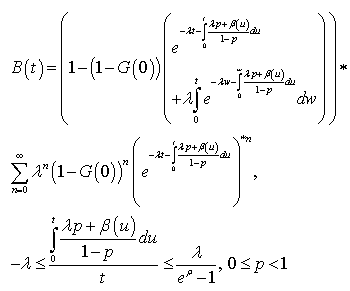
 system busy period length distribution function, being
system busy period length distribution function, being  the convolution operator.If
the convolution operator.If  (constant), (2) becomes, see[3],
(constant), (2) becomes, see[3], 
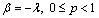 ,
,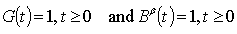 that is if the service distribution is degenerated at the origin with probability 1 it happens the same with the busy period distribution.Finally note that for
that is if the service distribution is degenerated at the origin with probability 1 it happens the same with the busy period distribution.Finally note that for 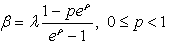
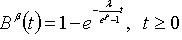 (purely exponential). And
(purely exponential). And 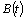 given by (5) satisfies
given by (5) satisfies 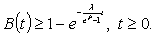 Calling
Calling 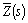 the busy cycle length Laplace transform, and noting that the
the busy cycle length Laplace transform, and noting that the 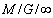 queue idle period is exponentially distributed with parameter
queue idle period is exponentially distributed with parameter 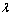 - as it happens for any queue system with Poisson arrivals at rate
- as it happens for any queue system with Poisson arrivals at rate 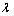 - and that the idle period and the busy period are independent for the
- and that the idle period and the busy period are independent for the 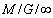 queue, see[4], it is obtained
queue, see[4], it is obtained 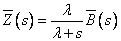
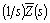 which inversion gives
which inversion gives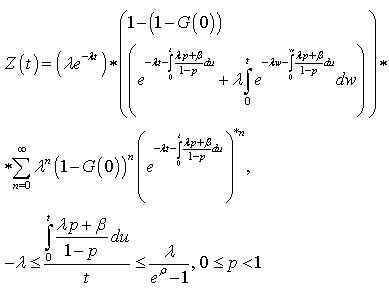
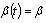 (constant) (9) becomes
(constant) (9) becomes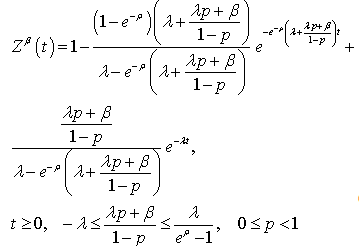
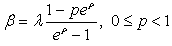
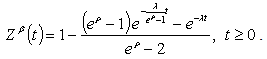 .And
.And 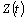 , given by (9), satisfies
, given by (9), satisfies 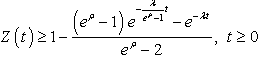
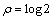 since
since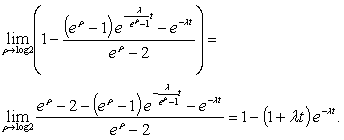 For
For 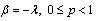
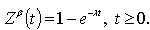 Finally, also for
Finally, also for 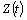 given by (9),
given by (9), 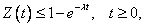
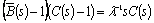 ,being
,being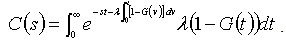 .Differentiating
.Differentiating 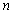 times, using Leibnitz’s formula and making
times, using Leibnitz’s formula and making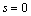 , results
, results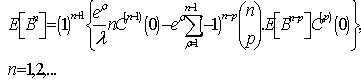
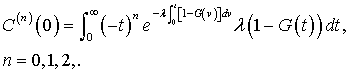
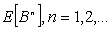 as a function of
as a function of 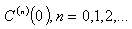 So it is possible to write exact expressions for the moments centred at the origin.Making
So it is possible to write exact expressions for the moments centred at the origin.Making 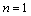 it is obtained
it is obtained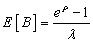
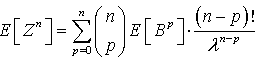
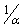 , see[6]. It is a parameter that characterizes the busy period distribution and contains information about all its moments. For the collection of service distributions (2) the “peak”, called
, see[6]. It is a parameter that characterizes the busy period distribution and contains information about all its moments. For the collection of service distributions (2) the “peak”, called 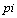 , is
, is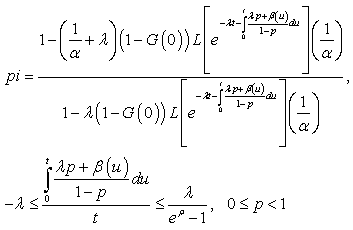
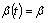 (constant), see[7],
(constant), see[7],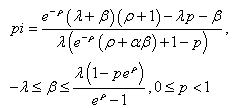
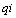 . It is easy to verify that
. It is easy to verify that 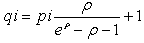 and, so, for the distributions given by collection (2) with
and, so, for the distributions given by collection (2) with 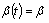 (constant), so collection (6), see again[7],
(constant), so collection (6), see again[7],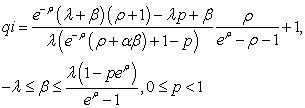
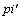 , for the service distributions given by the collection (2) is
, for the service distributions given by the collection (2) is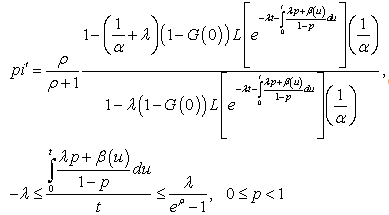
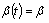 (constant), see[7],
(constant), see[7],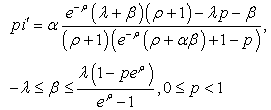
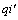 , given by
, given by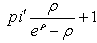 , for the service distributions given by the collection (6) is
, for the service distributions given by the collection (6) is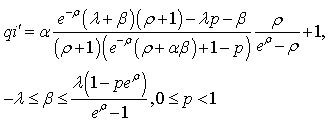
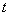 , gives the mean number of busy periods that begin in
, gives the mean number of busy periods that begin in 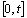 , see [9]. Calling it
, see [9]. Calling it 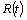 :
: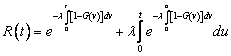
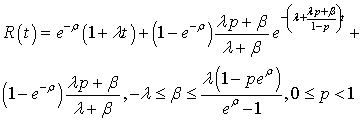
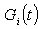 is the solution associated to
is the solution associated to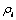 ,
, 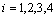 it is easy to see that
it is easy to see that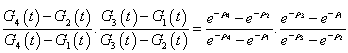
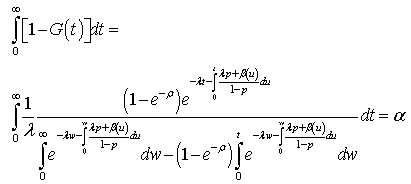 in accordance to the fact that (2) is a collection of positive random variables distribution functions.The density associated to
in accordance to the fact that (2) is a collection of positive random variables distribution functions.The density associated to 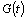 given by (2) is
given by (2) is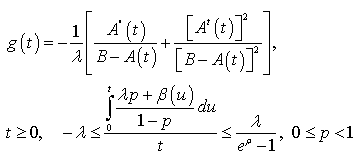
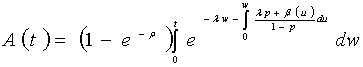 and
and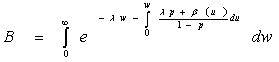 If
If 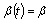 (constant), see[7],
(constant), see[7],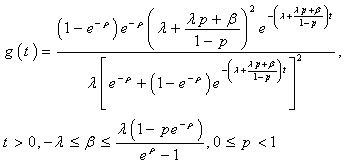
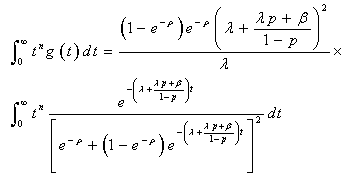
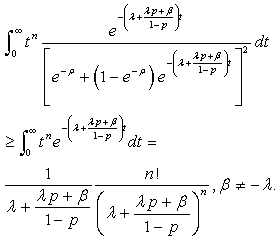 And,
And, 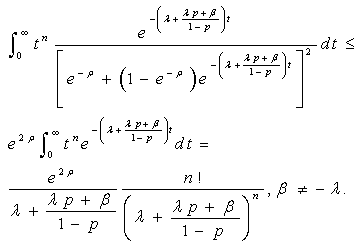 So, calling
So, calling 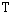 the random variable corresponding to:
the random variable corresponding to: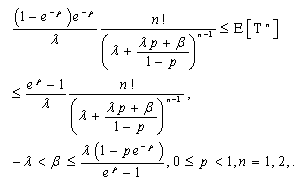
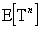 , guarantees its existence,For
, guarantees its existence,For 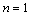 the expression (29) is useless because
the expression (29) is useless because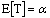 . Note, curiously, that the upper bound is
. Note, curiously, that the upper bound is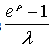 , the M/G/∞ system busy period mean value,For
, the M/G/∞ system busy period mean value,For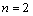 , subtracting to both bounds,
, subtracting to both bounds, 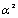 from expression (29) result bounds for
from expression (29) result bounds for 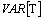 ,For
,For 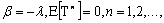 evidently.See, however, that (6) can be put like:
evidently.See, however, that (6) can be put like: 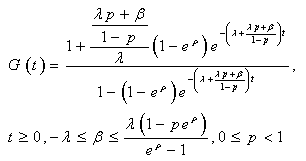
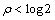 ,
,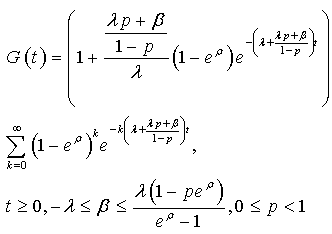
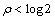 , can be easily derived. And, so, - For
, can be easily derived. And, so, - For 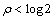
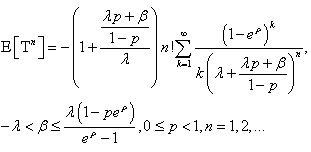
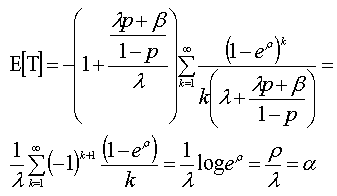 For
For 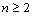 only a finite number of parcels in the infinite sum must be taken. Calling
only a finite number of parcels in the infinite sum must be taken. Calling  this number, to get an error lesser than
this number, to get an error lesser than  it is necessary to have simultaneously
it is necessary to have simultaneously 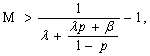
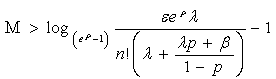 .So it is evident now that this distributions collection moments computation is a complex task. This was already true for the study of[10] where the results presented are a particular situation of these ones for
.So it is evident now that this distributions collection moments computation is a complex task. This was already true for the study of[10] where the results presented are a particular situation of these ones for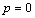 .The consideration of the approximation
.The consideration of the approximation 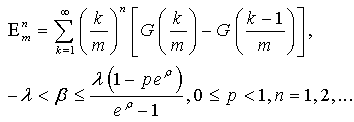
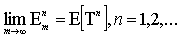 , see[11], that allow the numerical computation of the moments.
, see[11], that allow the numerical computation of the moments.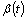 , defined in 1., that leads to the equation (1), the source of the results presented, is induced by the M/G/∞ transient probabilities monotony study, see[1] and[3]. Being well known the close relations existing among the transient behaviour and the busy period distributions, it is not surprising that the service distribution functions, solutions of (1), give rise to so friendly distributions to the M/G/∞ queue busy period. This is a quite unusual situation, that allows simple computations for the probabilities and parameters of the busy period and busy cycle.This so simple structure lies on the exponential distribution and the deterministic one. In many of the situations seen there are purely deterministic and exponential distributions, mixtures of deterministic and exponential distributions and mixtures of two exponential distributions. The great presence of the exponential distribution in this context is due certainly to the so friendly properties of the Poisson Process and to the structure of the function resulting from the inversion of the Laplace Transform given by (4).Even the stochastic processes related with this queue become quite simple. They are very close to the Poisson Process and in certain situations are even Poisson Processes.In conclusion, all of this results in a very simple expression for the inversion of (4), with the service distributions solutions of (1). In consequence, as it was shown in this work, the distribution functions and the parameters for the busy period and, consequently, for the busy cycle result very simple to compute and interpret.Many of these results are true for other service distribution functions, in the case of insensibility: parameters that depend on the service distribution only through its mean. Some others may result in good approximations.Note still that when the distribution functions for
, defined in 1., that leads to the equation (1), the source of the results presented, is induced by the M/G/∞ transient probabilities monotony study, see[1] and[3]. Being well known the close relations existing among the transient behaviour and the busy period distributions, it is not surprising that the service distribution functions, solutions of (1), give rise to so friendly distributions to the M/G/∞ queue busy period. This is a quite unusual situation, that allows simple computations for the probabilities and parameters of the busy period and busy cycle.This so simple structure lies on the exponential distribution and the deterministic one. In many of the situations seen there are purely deterministic and exponential distributions, mixtures of deterministic and exponential distributions and mixtures of two exponential distributions. The great presence of the exponential distribution in this context is due certainly to the so friendly properties of the Poisson Process and to the structure of the function resulting from the inversion of the Laplace Transform given by (4).Even the stochastic processes related with this queue become quite simple. They are very close to the Poisson Process and in certain situations are even Poisson Processes.In conclusion, all of this results in a very simple expression for the inversion of (4), with the service distributions solutions of (1). In consequence, as it was shown in this work, the distribution functions and the parameters for the busy period and, consequently, for the busy cycle result very simple to compute and interpret.Many of these results are true for other service distribution functions, in the case of insensibility: parameters that depend on the service distribution only through its mean. Some others may result in good approximations.Note still that when the distribution functions for 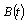 and
and 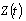 are a little more complicated, simple bounds are presented. In the field of Queuing Theory this situation seems unique, there having no news of anything similar.
are a little more complicated, simple bounds are presented. In the field of Queuing Theory this situation seems unique, there having no news of anything similar. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML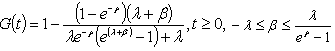 . Revista Portuguesa de Gestão, II, 67-69
. Revista Portuguesa de Gestão, II, 67-69