Bhaskar Srivastava
Department of Mathematics and Astronomy, University of Lucknow, Lucknow, India
Correspondence to: Bhaskar Srivastava , Department of Mathematics and Astronomy, University of Lucknow, Lucknow, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
From a continued fraction analogous to Rogers-Ramanujan continued fraction we have theta functions analogous to Ramanujan’s functions G(q) and H(q). We find certain identities for these analogous theta functions using Jacobi’s triple product identity, thus having a unified approach. We also find some modular equations.
Keywords:
q-Hypergeometric Series, Jacobi’s Triple Product Identity, Theta Functions
Cite this paper:
Bhaskar Srivastava , "Identities for Analogous Ramanujan’s Functions by Jacobi’s Triple Product Identity", American Journal of Mathematics and Statistics, Vol. 2 No. 1, 2012, pp. 25-28. doi: 10.5923/j.ajms.20120201.06.
1. Introduction
In[5] considering the continued fraction for 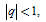
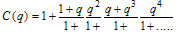 | (1.1) |
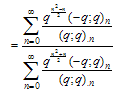 | (1.2) |
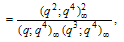 | (1.3) |
which, I think, is analogous to the famous celebrated Rogers-Ramanujan continued fraction 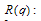
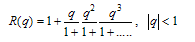 | (1.4) |
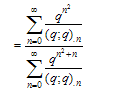 | (1.5) |
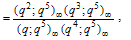 | (1.6) |
I thought of defining the theta functions: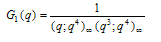 | (1.7) |
And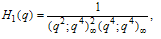 | (1.8) |
which are analogous to Ramanujan’s theta functions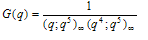 | (1.9) |
and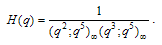 | (1.10) |
2. Basic Notation
The following standard q-hypergeometric notations will be used:For 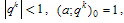 and for n ,
and for n , 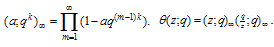 | (2.1) |
We also have the Ramanujan’s functions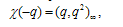 | (2.2) |
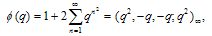 | (2.3) |
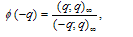 | (2.4) |
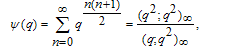 | (2.5) |
and Jacobi’s triple product identity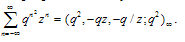 | (2.6) |
We shall be needing the following two Lemmas of Ramanujan [2, Entry 29, p 45]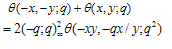 | (2.7) |
and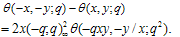 | (2.8) |
Also [2, Entry 30 (ii)-(iii), p 46]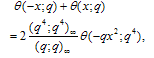 | (2.9) |
and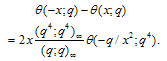 | (2.10) |
Theorem 1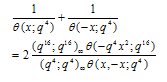 | (3.1) |
and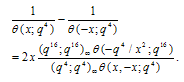 | (3.2) |
Proof of Theorem 1Proof of (3.1)where we have used (2.9) in the last step to prove (3.1).Proof of (3.2)Proof is exactly the same as in (3.1) only we have used (2.10) in the last step to obtain (3.2).Theorem 2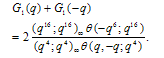 | (3.3) |
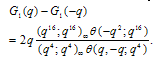 | (3.4) |
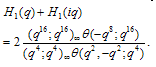 | (3.5) |
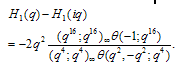 | (3.6) |
Proof of Theorem 2By definitionand Proof of (3.3) and (3.4)Put in (3.1) and (3.2) to get (3.3) and (3.4), respectively.Proof of (3.5) and (3.6)Put x=q2 in (3.1) and (3.2) to get (3.5) and (3.6), respectively.Theorem 3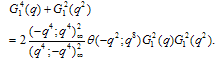 | (3.7) |
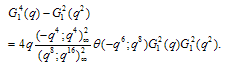 | (3.8) |
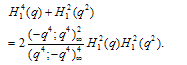 | (3.9) |
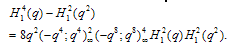 | (3.10) |
Proof of Theorem 3Proof of (3.7)we have used (2.7) in the penultimate step to obtain (3.7).Proof of (3.8)The proof is exactly the same as of (3.7) only we use (2.8) in penultimate step to obtain (3.8).Proof of (3.9)we have used (2.7) in the penultimate step to obtain (3.9).Proof of (3.10)The proof is exactly the same as in (3.9) only we have used (2.8) to obtain (3.10).Theorem 4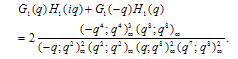 | (3.11) |
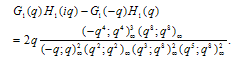 | (3.12) |
Proof of Theorem 4Proof of (3.11)we have used (2.7) in the penultimate step to obtain (3.11).Proof of (3.12)The proof is exactly the same, only we use (2.8) in the penultimate step to obtain (3.12).Theorem 5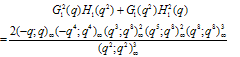 | (3.13) |
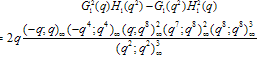 | (3.14) |
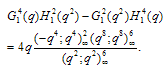 | (3.15) |
Proof of Theorem 5Proof of (3.13)we have used (2.7) in the penultimate step to obtain (3.13).Proof of (3.14)The proof is same only in the penultimate step we have used (2.8) to obtain (3.14).Proof of (3.15)Multiply (3.13) and (3.14) to have (3.15).
4. Modular Equation
We prove the following :Theorem 6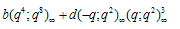 | (4.1) |
Proof of Theorem 6Writing (4.1) as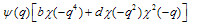 | (4.2) |
Corollary 1Put in (4.2), to getCorollary 2Put in (4.2), to getCorollary 3Put in (4.2), to getCorollary 4Put in (4.2), to get
References
| [1] | G. E. Andrews, Application of basic hypergeometric functions, SIAM Rev.16 (1974), 441-484 |
| [2] | B.C. Berndt, Ramanujan’s Notebooks, Part III, Springer-Verlag, New York, 1991 |
| [3] | W. Chu and Q. Yan, Jacobi’s triple product identity and theta function identities, Math. Commun. 16 (2011), 191-203 |
| [4] | G. Gasper and M. Rahman, Basic Hypergeometric Series, Cambridge University Press, Cambridge (1990) |
| [5] | Bhaskar Srivastava, on modular equations and Lambert series for a continued fraction of Ramanujan, Bull. Math. Anal. Appl. 3 (2011), 148-155 |

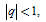
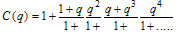
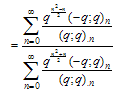
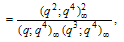
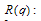
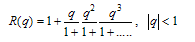
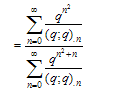
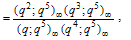
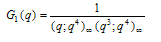
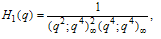
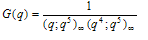
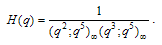
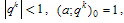 and for n ,
and for n , 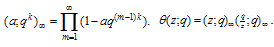
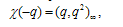
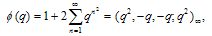
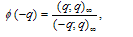
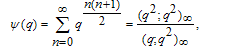
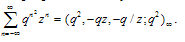
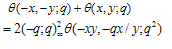
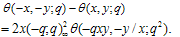
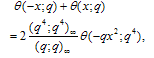
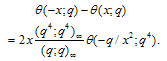
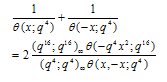
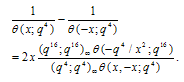
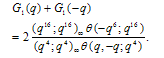
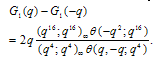
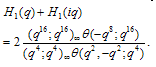
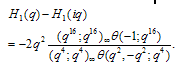
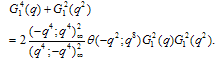
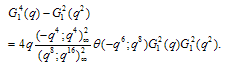
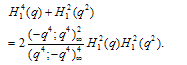
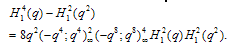
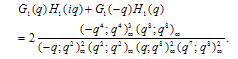
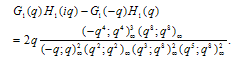
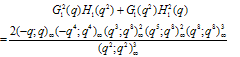
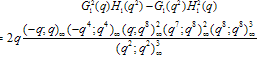
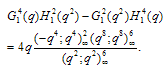
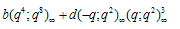
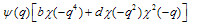
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML