-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2011; 1(1): 21-25
doi: 10.5923/j.ajms.20110101.04
On Complementary Edge Magic Labeling of Certain Graphs
1Research Scholar, Singhania University, Pacheri Bari, Dist. Jhunjhunu, Rajasthan, India. E-mail:sanjay_online1@yahoo.co.in
2Academic Dean, HMS institute of Technology, Tumkur, Karnataka, India
Correspondence to: Sanjay Roy , Research Scholar, Singhania University, Pacheri Bari, Dist. Jhunjhunu, Rajasthan, India. E-mail:sanjay_online1@yahoo.co.in.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
By G(p, q) we denote a graph having p vertices and q edges, by V(G) and E(G) the vertex set and the edge – set of G respectively. But the vertices and edges are called the elements of the graph. A (p, q) – graph G is called the edge – magic if there exists a bijective function f: V(G) U E(G) à {1,2,…….,p+q} such that f(u)+f(v)+f(uv)=k is a constant called the valence of f for any edge uv of G. Given an edge magic f of a graph G(p, q) the function 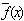 such that
such that 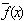 =p+q+1-f(x) for all elements of G is said to be complementary to f(x) or complementary edge magic labeling
=p+q+1-f(x) for all elements of G is said to be complementary to f(x) or complementary edge magic labeling 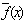 . The purpose of this article is to search for certain graphs Km, n (m, n ≥ 1), Cn (n ≥ 3), np2, f n (fan) Bn (bwk) and nG (n ≥ 2) where G is bipartite or tripartite which have complementary edge magic strength.
. The purpose of this article is to search for certain graphs Km, n (m, n ≥ 1), Cn (n ≥ 3), np2, f n (fan) Bn (bwk) and nG (n ≥ 2) where G is bipartite or tripartite which have complementary edge magic strength.
Keywords: Edge-Magic Labeling, Complementary Edge Magic Labeling
Cite this paper: Sanjay Roy , D.G. Akka , "On Complementary Edge Magic Labeling of Certain Graphs", American Journal of Mathematics and Statistics, Vol. 1 No. 1, 2011, pp. 21-25. doi: 10.5923/j.ajms.20110101.04.
Article Outline
1. Introduction
- The subject of edge – magic labelings of graphs had its origins three decades ago in the work of Kotzing and Rosa [9,10] on what they called magic valuations of graphs (which are also commonly known as edge-magic total labeling see[4]). Interest in these labelings has been lately rekindled by a paper on the subject due to Ringel and Llado [11]. Shortly after this, Enomoto, Llado, Nakamigawa and Ringel[3] defined a more restrictive form of edge-magic labelings namely super edge magic labelings which Wallis [12] refers to as strong edge – magic labelings.By G(p, q), we denote a graph having p vertices and q edge, by V(G) and E(G), the vertex set and the edge-set of G respectively. But the vertices and edges are called the elements of the graph G. A graph (p, q) is said to have an edge magic with the magic constant k (which is independent on the choice of any edge uv of G) if there exists a one one– to –one mapping f:V(G) U E(G) à {1, 2,……,p+q} such that f(u) + f(v) +f(uv) =k for all uv ∈ E (G). If such a labeling exists, then magic constant k is called valence of f and G is said to be edge –magic graph. Given an edge magic f of a graph G (p, q), the Function f(x) such that
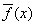 = p+q+1-f(x) for all elements x ∈G is said to be complementary to f(x).Two edge magic f1 and f2 of G are equivalent if f1=f2 orf1=
= p+q+1-f(x) for all elements x ∈G is said to be complementary to f(x).Two edge magic f1 and f2 of G are equivalent if f1=f2 orf1=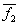 . An edge magic f of G is said to be self complementary edge magic if f=
. An edge magic f of G is said to be self complementary edge magic if f=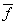
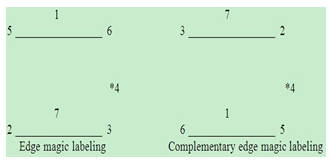 | Figure 1. |
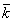 where the minimum is taken over all complementary edge magic labeling of G. cems (G) = min {
where the minimum is taken over all complementary edge magic labeling of G. cems (G) = min {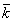 :
: 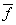 is an complementary edge magic labeling of G}.In this paper, the complementary edge magic strength of some well known graphs such as Km, n (m,n ≥ 1), Cn (n ≥ 3), np2 (n ≥ 1), fn, Bn and nG (n ≥ 2) where G is bipartite or tripartite are obtained. The reader is directed to Chartered and Lesniak[2] or Hartefield and Ringel[8] for all additional terminology not provided in this paper. The following theorem is every useful for the main results.Theorem A [1] An complementary edge – magic graph G satisfies the following equation
is an complementary edge magic labeling of G}.In this paper, the complementary edge magic strength of some well known graphs such as Km, n (m,n ≥ 1), Cn (n ≥ 3), np2 (n ≥ 1), fn, Bn and nG (n ≥ 2) where G is bipartite or tripartite are obtained. The reader is directed to Chartered and Lesniak[2] or Hartefield and Ringel[8] for all additional terminology not provided in this paper. The following theorem is every useful for the main results.Theorem A [1] An complementary edge – magic graph G satisfies the following equation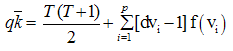 where
where 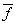 is complementary edge magic labeling of G and T=p+q.Main ResultsIn this section we proceed to study the complementary edge magic strength of Km, n, Cn, fn=Pn+k1 and Bn = K1, n x K2 and nG, where G is bipartite or tripartite.Theorem1. A complete bipartite graph Km, n is complementary edge magic strength if m, n ≥ 1.Proof: Let G be a complete bipartite graph Km, n with vertex set V partitioned into two subject V1 and V2 where V1={u1, u2,………um} and V2={v1,v2,……vn} andlet f: VUEà {1,2,…..,m+n+mn}Then,
is complementary edge magic labeling of G and T=p+q.Main ResultsIn this section we proceed to study the complementary edge magic strength of Km, n, Cn, fn=Pn+k1 and Bn = K1, n x K2 and nG, where G is bipartite or tripartite.Theorem1. A complete bipartite graph Km, n is complementary edge magic strength if m, n ≥ 1.Proof: Let G be a complete bipartite graph Km, n with vertex set V partitioned into two subject V1 and V2 where V1={u1, u2,………um} and V2={v1,v2,……vn} andlet f: VUEà {1,2,…..,m+n+mn}Then,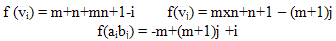 It is easy to see that f extends to a complementary edge magic labeling of Km, n with the magic constant
It is easy to see that f extends to a complementary edge magic labeling of Km, n with the magic constant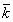 .
.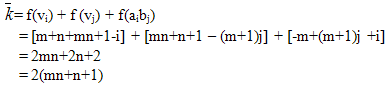 Complementary edge magic strength: Now by Theorem A
Complementary edge magic strength: Now by Theorem A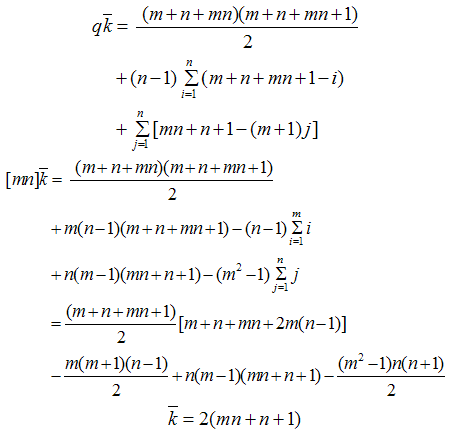 Thus scems (K m, n) = 2(mn+n+1)The following theorem is the complementary edge magic strength of cycle Cn for every integer n ≥ 3.Theorem2. The cycle Cn is complementary edge magic and complementary edge magic strength is
Thus scems (K m, n) = 2(mn+n+1)The following theorem is the complementary edge magic strength of cycle Cn for every integer n ≥ 3.Theorem2. The cycle Cn is complementary edge magic and complementary edge magic strength is 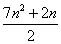 where n is an integer. Proof: Let C be the cycle with V (Cn) = {v i: 1 ≤ i ≤ n} and E (Cn) = {vi: v i+1 : 1 ≤ i ≤ n2} where i is taken modulo n (replacing o by n) We discuss the following cases.Case I: n is odd say n=2m +1 where m is positive integer.Consider the function f: V(G) U E (G) à {1,2,…,2n}Defined as
where n is an integer. Proof: Let C be the cycle with V (Cn) = {v i: 1 ≤ i ≤ n} and E (Cn) = {vi: v i+1 : 1 ≤ i ≤ n2} where i is taken modulo n (replacing o by n) We discuss the following cases.Case I: n is odd say n=2m +1 where m is positive integer.Consider the function f: V(G) U E (G) à {1,2,…,2n}Defined as 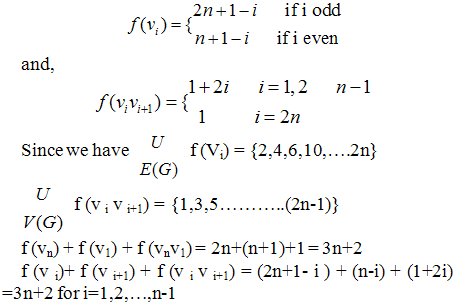 Thus f is a complementary edge magic of cycle Cn with magic constant 3n+2Complementary edge – magic string:
Thus f is a complementary edge magic of cycle Cn with magic constant 3n+2Complementary edge – magic string: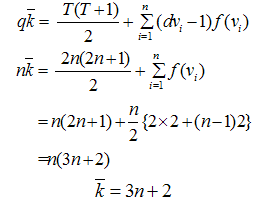 Case 2. n ≡ o (mod 4) say n = 4l where l is the positive integer, f is defined as
Case 2. n ≡ o (mod 4) say n = 4l where l is the positive integer, f is defined as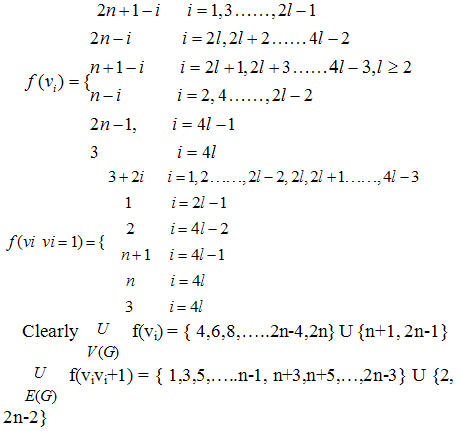 Next we prove thatf(vi)+f(vi+1)+f(vivi+1) = for all i = 1,2,..,4lSub case 2.1 Let i ∈ {4, 6, 8.., 2n-4,2n} U {n+1,2n-1} Thenf (vi)+f (vi+1)+f (vivi+1) = (2n+1-i)+(n-i-1)+(3+2i) =3(n+1)Sub case 2.2 Let i = 2l-1 thenf (v2l-1)+f (v2l)+ f (v2l-1v2l)=(2n-2l+2)+(2n-2l)+1=3(n+1)Sub case 2.3 Let i ∈ {2l, 2l+2,…, 4l-4} Thenf (vi)+f (vi+1)+f (vivi+1) = (2n-i)+(n-i)+3+2i=3(n+1)Sub case 2.4 Let i = 2l-2 Thenf (v4l-2)+f (v4l-1)+f (v4l-2 v4l-1)=(2n+2)+(2n-1)+2=3(n+1)Sub case 2.5 Let I ∈ {2l+1, 2l+3,..,4l-3}, Thenf (vi)+f(vi+1)+f (vivi+1) = (n+1-i)+(2n-1-i)+(3+2i)=3(n+1)Sub case 2.6 Let i ∈ {2l+1, 2l+3,…4l-3} Thenf (vi)+f (vi+1) + f (vivi+1)= (n-i)+(2n-i)+(3+2i)=3(n+1)Sub case 2.7 Let i = 4l-1. Thenf (v4l-1)+f (v4l)+f (v4l-1v4l)=(2n-1)+(3)+(n+1)=3(n+1)Sub case 2.8 Let i = 4l. Thenf (v4l)+f(v1)+f (v4lv1)= 3+(2n)+n=3(n+1)Therefore is a complementary edge magic of the cycle Cn with the magic Constant= 3 (n+1)Complementary edge magic strength:
Next we prove thatf(vi)+f(vi+1)+f(vivi+1) = for all i = 1,2,..,4lSub case 2.1 Let i ∈ {4, 6, 8.., 2n-4,2n} U {n+1,2n-1} Thenf (vi)+f (vi+1)+f (vivi+1) = (2n+1-i)+(n-i-1)+(3+2i) =3(n+1)Sub case 2.2 Let i = 2l-1 thenf (v2l-1)+f (v2l)+ f (v2l-1v2l)=(2n-2l+2)+(2n-2l)+1=3(n+1)Sub case 2.3 Let i ∈ {2l, 2l+2,…, 4l-4} Thenf (vi)+f (vi+1)+f (vivi+1) = (2n-i)+(n-i)+3+2i=3(n+1)Sub case 2.4 Let i = 2l-2 Thenf (v4l-2)+f (v4l-1)+f (v4l-2 v4l-1)=(2n+2)+(2n-1)+2=3(n+1)Sub case 2.5 Let I ∈ {2l+1, 2l+3,..,4l-3}, Thenf (vi)+f(vi+1)+f (vivi+1) = (n+1-i)+(2n-1-i)+(3+2i)=3(n+1)Sub case 2.6 Let i ∈ {2l+1, 2l+3,…4l-3} Thenf (vi)+f (vi+1) + f (vivi+1)= (n-i)+(2n-i)+(3+2i)=3(n+1)Sub case 2.7 Let i = 4l-1. Thenf (v4l-1)+f (v4l)+f (v4l-1v4l)=(2n-1)+(3)+(n+1)=3(n+1)Sub case 2.8 Let i = 4l. Thenf (v4l)+f(v1)+f (v4lv1)= 3+(2n)+n=3(n+1)Therefore is a complementary edge magic of the cycle Cn with the magic Constant= 3 (n+1)Complementary edge magic strength: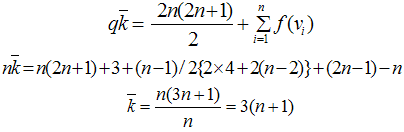 Case 3. n ≡ 2 (mod 4) that is n = 4l+2. Define the function
Case 3. n ≡ 2 (mod 4) that is n = 4l+2. Define the function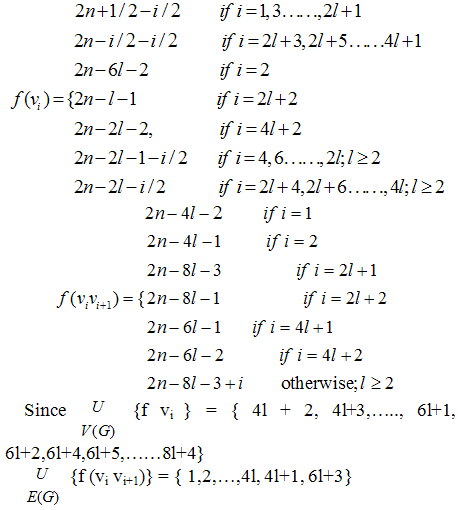 Next we prove that f (vi)+f (vi+1)+ f (vivi+1) = for all i = 1,2,…..,4l+2Subcase 3.1 Let i = 1 Then
Next we prove that f (vi)+f (vi+1)+ f (vivi+1) = for all i = 1,2,…..,4l+2Subcase 3.1 Let i = 1 Then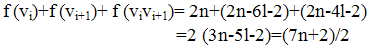 Sub case 3.2 Let i = {3,5,..,2l-1} Then
Sub case 3.2 Let i = {3,5,..,2l-1} Then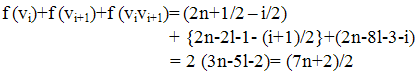 Sub case 3.3 Let i = 2l+1. Then
Sub case 3.3 Let i = 2l+1. Then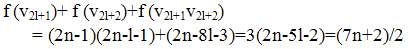 Sub case 3.4 Let i = {2l+3, 2l+5,…, 4l-1} Then
Sub case 3.4 Let i = {2l+3, 2l+5,…, 4l-1} Then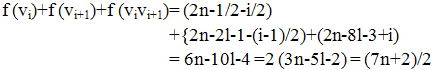 Sub case 3.5 Let i = 4l+1. Then
Sub case 3.5 Let i = 4l+1. Then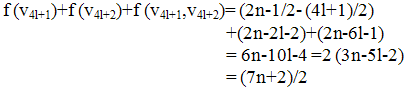 Sub case 3.6 Let i = 2. Then
Sub case 3.6 Let i = 2. Then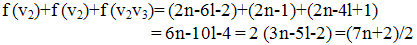 Sub case 3.7 Let i = 2k+2. Then
Sub case 3.7 Let i = 2k+2. Then 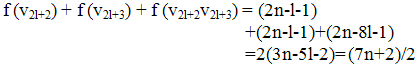 Sub case 3.8 Let i = 4l+2. Then
Sub case 3.8 Let i = 4l+2. Then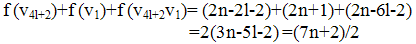 Sub case 3.9 Let i ∈ {4,6,…2k}. Then
Sub case 3.9 Let i ∈ {4,6,…2k}. Then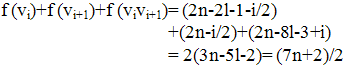 Sub case 3.10 Let i ∈ {2l+4, 2l+6,….4l}. Then
Sub case 3.10 Let i ∈ {2l+4, 2l+6,….4l}. Then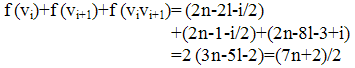 Thus f is a complementary edge magic function of the cycle C4l+2 with the magic constant
Thus f is a complementary edge magic function of the cycle C4l+2 with the magic constant 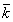 =2(3n-5l-2)= (7n+2)/2Complementary edge magic strength:
=2(3n-5l-2)= (7n+2)/2Complementary edge magic strength: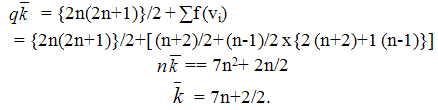 Theorem 3. Let G = nР2 be a regular graph of degree one. Then G is a Complementary edge magic strength if and Only if n is odd.Proof: Since (3n+1)/2 must be necessarily an integer. Hence it follows that n must be odd say n= 2l+1Let u1, u2, …. un and v1, v2,….,vn; u1v1, u2v2… unvn be vertices and edges of G respectively. Define f by
Theorem 3. Let G = nР2 be a regular graph of degree one. Then G is a Complementary edge magic strength if and Only if n is odd.Proof: Since (3n+1)/2 must be necessarily an integer. Hence it follows that n must be odd say n= 2l+1Let u1, u2, …. un and v1, v2,….,vn; u1v1, u2v2… unvn be vertices and edges of G respectively. Define f by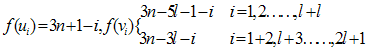 And
And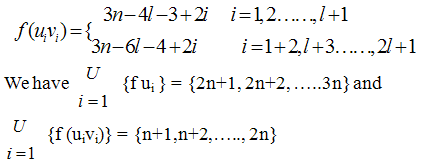 Now we show that
Now we show that 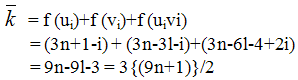 Complementary edge magic strength:
Complementary edge magic strength: Theorem 4. The fan fn = Pn+K1 is a complementary edge magic for any positive integer nProof . Let V (fn) = {u} U { vi :1≤ i ≤ n }And E (fn) = { uvi : 1≤i≤n} U {vivi+1 : 1≤i≤n-1}Now define the function f: V (G) U E(G)"{1,2,…..,3n} as follows
Theorem 4. The fan fn = Pn+K1 is a complementary edge magic for any positive integer nProof . Let V (fn) = {u} U { vi :1≤ i ≤ n }And E (fn) = { uvi : 1≤i≤n} U {vivi+1 : 1≤i≤n-1}Now define the function f: V (G) U E(G)"{1,2,…..,3n} as follows 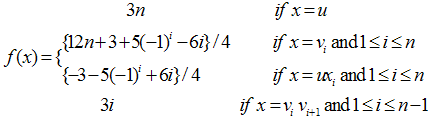 Observe that f(x)+f(y)+f(xy)=6n for every edge xy ∈ E (fn)Also notice that alternative type labeling is as follows:
Observe that f(x)+f(y)+f(xy)=6n for every edge xy ∈ E (fn)Also notice that alternative type labeling is as follows: 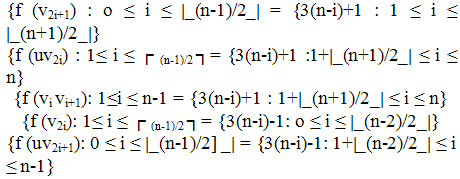 And f (u) = 3n. Thus all integers 1,2,…,3n are used exactly once. Hence f is an complementary edge magic labeling of fn with magic constant (valence) 6n.Complementary edge magic strength :
And f (u) = 3n. Thus all integers 1,2,…,3n are used exactly once. Hence f is an complementary edge magic labeling of fn with magic constant (valence) 6n.Complementary edge magic strength :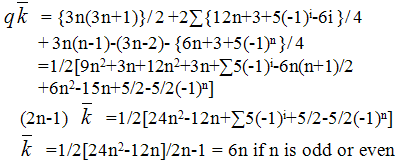 Theorem 5. The book Bn=K1,n x K2 is complementary edge magic strength for any positive integer nProof. Let Bn be the book defined as follows:V (Bn) = {uv}U{uivi :1≤ i ≤ n} and E (Bn) = {uv}U{uui, vvi, uivi : 1 ≤ i≤n}Now consider the function f : V(Bn)UE(Bn)" {1,2,..,5n+3}Where
Theorem 5. The book Bn=K1,n x K2 is complementary edge magic strength for any positive integer nProof. Let Bn be the book defined as follows:V (Bn) = {uv}U{uivi :1≤ i ≤ n} and E (Bn) = {uv}U{uui, vvi, uivi : 1 ≤ i≤n}Now consider the function f : V(Bn)UE(Bn)" {1,2,..,5n+3}Where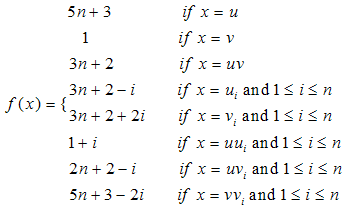 Finally observe that f is complementary edge magic labeling of Bn having valence 8n+6Complementary edge magic strength:
Finally observe that f is complementary edge magic labeling of Bn having valence 8n+6Complementary edge magic strength: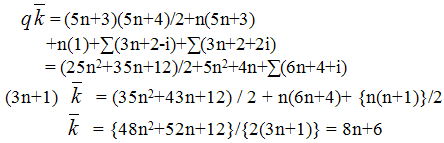 This section has a tool that allows us to generate infinite classes of disconnected complementary edge magic n- partite graphs with relative case where n = 2,or 3. Previously no such a technique was available for graphs within those classes sec[6] except in[5].Theorem 6. If G is a complementary edge magic bipartite or tripartite graph and n is odd then nG (n ≥ 2) is complementary edge magic. Proof. Assume that n≥3. If (p,q) graph G is a complementary edge magic bipartite or tripartite graph with partite sets A, B, C [Let C=Φ if G is bipartite ] then let E(G) = AB U AC U BC where the juxta-position of two partite sets denotes the set of edges between those two sets. Let f :V (G)UE(G)"{1,2,…..,p+q} to be an arbitrary complementary edge magic labeling of G. Then X ≡ nG to be the graph with vertex setV(X)=
This section has a tool that allows us to generate infinite classes of disconnected complementary edge magic n- partite graphs with relative case where n = 2,or 3. Previously no such a technique was available for graphs within those classes sec[6] except in[5].Theorem 6. If G is a complementary edge magic bipartite or tripartite graph and n is odd then nG (n ≥ 2) is complementary edge magic. Proof. Assume that n≥3. If (p,q) graph G is a complementary edge magic bipartite or tripartite graph with partite sets A, B, C [Let C=Φ if G is bipartite ] then let E(G) = AB U AC U BC where the juxta-position of two partite sets denotes the set of edges between those two sets. Let f :V (G)UE(G)"{1,2,…..,p+q} to be an arbitrary complementary edge magic labeling of G. Then X ≡ nG to be the graph with vertex setV(X)=  (AiBiUAiCiUBiCi) where xi ∈ Yi for 1 ≤ i ≤ n if and only if x ∈ Y (Y is one of the sets A,B,C,AB,AC,BC) Consider the labeling g : V(X)UE(X)"{1,2,…..n (p+q)} such that
(AiBiUAiCiUBiCi) where xi ∈ Yi for 1 ≤ i ≤ n if and only if x ∈ Y (Y is one of the sets A,B,C,AB,AC,BC) Consider the labeling g : V(X)UE(X)"{1,2,…..n (p+q)} such that 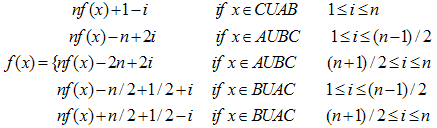 Clearly g is a complementary edge magic labeling of X with valence g(u)+g(v)+g(uv)=2n(p+q)-3(n-1)/2 for each edge uv ∈ E(X) where kf is the valence of f. Next to observe that g(V(H)UE(H))={1,2,…,n(p+q) is spread by the function g to the entirety of its range.In the above theorem n can not be even for Kotzig and Rosa[9] have shown that the forest nP2 is edge magic if and only n is oddImmediately the corollary follows from above Theorem Corollary: If n is odd and m>1 then 2-regular graph nC2m is complementary edge magic.Poof. Kotzig and Rosa have shown that all cycles are edge magic. But an alternative labeling of even cycles can be found in[7].
Clearly g is a complementary edge magic labeling of X with valence g(u)+g(v)+g(uv)=2n(p+q)-3(n-1)/2 for each edge uv ∈ E(X) where kf is the valence of f. Next to observe that g(V(H)UE(H))={1,2,…,n(p+q) is spread by the function g to the entirety of its range.In the above theorem n can not be even for Kotzig and Rosa[9] have shown that the forest nP2 is edge magic if and only n is oddImmediately the corollary follows from above Theorem Corollary: If n is odd and m>1 then 2-regular graph nC2m is complementary edge magic.Poof. Kotzig and Rosa have shown that all cycles are edge magic. But an alternative labeling of even cycles can be found in[7].  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML