1. Introduction

The idea of common fixed point was initially given by Jungck[3], where the mappings considered were commuting. There after many generalizations of this common fixed point result were obtained by several mathematicians viz., Hadzic[2], Meade and Singh[11], Pathak[7], Yeh[13] etc. The commutativity condition of mappings was further replaced by a weaker type of notion viz., weakly commuting mappings as introduced by Sessa[8]. Several common fixed point theorems have been proved for such mappings by many authors viz., Sessa et. al.[9], Fisher and Sessa[1] and others. The notion of weak commutativity has been further weakened by the notion of compatible mappings, introduced by Jungck[4] which gave a new direction towards more comprehensive results in the context of common fixed point in metric fixed point theory. In this paper we obtain some common fixed point results for compatible mappings satisfying more general inequality condition which mainly generalize the results of Mukherjee[6], Som[10] and others in turn.

1.1. Definition I (Sessa[8]) :

Two self mappings A and S of a metric space (X, d) are called weakly commuting if

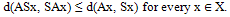
1.2. Definition II (Jungck[4]) :

Let f and g be two self maps on a metric space (X,d). f and g are called compatible if

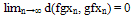whenever {x_n} is a sequence such that

lim_n→∞ fx_n = lim_n→∞gx_n = t for some t in X.

The Banach contraction theorem assures fixed point for a mapping which is necessarily continuous. However Taskovic[12] proved the following fixed point result for a self mapping which is not necessarily continuous.

1.3. Theorem I

Let T be a self mapping of a complete metric space (X,d) satisfying

(1) ad(Tx,Ty) + bd(x,Tx) + cd(y,Ty) - min {d(Tx,y),

d(x,Ty)} ≤ qd(x,y)

with a > q+1 and a+c > 0. Then T has a unique fixed point in X.

Generalizing the above result of Taskovic and that of Mukherjee[6] for common fixed point of two mappings, Som[10] obtained the following results.

1.4. Theorem II

Let T and S be two self mappings of a complete metric space (X,d) satisfying

(2) ad (Tx,Sy) + bd (x,Tx) + cd (y,Sy) – min {d(x,Sy),

d (Tx,y)} ≤ q d(x,y)

for all x,y ∈ X, where a,b,c ≥ 0, q > 0 with a > q+1 and a+c > 0. Then T and S have a unique common fixed point.

1.5. Theorem 1.3.

Let (X,d) be a complete metric space and T and S be a self mappings of X satisfying

(3) ad (Tx,Sy) + bd(x,Tx) + cd(y,Sy) – min{ d(x,Sy),

d(Tx,y)} ≤ q max{d(x,y), d(x,Tx), d(y,Sy),

[d(x,Sy) + d(Tx,y)]/2}

for all x,y ∈ X, where a,b,c ≥ 0 , q > 0 with a > q +1 and a + c > 0. Then T and S have a unique common fixed point.

Unifying the mapping conditions of above theorems we obtain few common fixed point results in the next section.

2. Main Results

Our first theorem extends the result of Som[10] in respect of the mapping condition.

2.1. Theorem I

Let A be a self mapping of a complete metric space (X,d) and S ,T be two continuous self mapping of X satisfying

(i) the pairs {A,S} and {A,T} are compatible with

A(X)⊂S(X) ∩T(X).

(ii) ad(Ax,Ay) + bd(Sx,Ty) + cd(Sx,Ax) ≤ ф{d(Sx,Ty),

d(Sx,Ax), d(Sx,Ay), d(Ty,Ax), d(Ty,Ay)}

where a+b+c > 1 and ф: R₊⁵→R₊ is non-decreasing in each coordinate variable and for any t > 0, ф( t, t, a₁t, a₂t, t) < t , a₁ + a₂ = 3. Then A, S and T have a unique common fixed point in X.

Proof: Let x₀ be any arbitrary point in X. Then Ax₀ ∈X. Since A(X) ⊂ S(X), there exists a point x₁ ∈ X such that Ax₀ = Sx₁. Further since A(X) ⊂ T(X), there is a point x₂ ∈ X such that Ax₁ = Tx₂. In general we have the sequence {x_n} in X such that

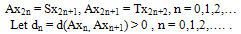Here we claim that {d_n} is a decreasing sequence. Suppose that d_2n > d_2n-1 for some n. Putting x = x_2n+1, y = x_2n in (ii), we get

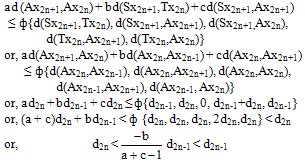i.e., a contradiction. Therefore {d_n} is decreasing sequence of non negative reals, so it converges to zero. Now, we show that {Ax_n} is a Cauchy sequence. Since lim_n→∞ d_n = 0, it is sufficient to show that {Ax_2n} is a Cauchy sequence. Suppose that it is not so. Then there is an ε > 0 and for each even integer 2k, k = 0,1,2,… there exists even integer 2n(k) and 2m(k) with 2k < 2n(k) < 2m(k) such that

(iii) d(Ax_2n(k), Ax_2m(k)) > ε

Let for each even integer 2k, 2m(k) be least positive integer exceeding 2n(k) satisfying (iii) ,

then

(iv) d(Ax_2n(k),Ax_2m(k)-2) ≤ ε and d(Ax_2n(k),Ax_2m(k)) > ε

As such for each even integer 2k, we have

ε < d(Ax_2n(k),Ax_2m(k) ) ≤ d(Ax_2n(k),Ax_2m(k)-2 ) + d_2m(k)-2

+ d_2m(k)-1

So by (iv) and as k→∞, we get

(v) lim_k→∞ d(Ax_2n(k), Ax_2m(k)) = ε

Now using (v) in the triangle inequalities

|d(Ax_2n(k), Ax_2m(k)-1) – d(Ax_2n(k), Ax_2m(k))| ≤ d_2m(k)-1

and |d(Ax_2n(k)+1, Ax_2m(k)-1) – d(Ax_2n(k), Ax_2m(k))|

≤ d_2m(k)-1 + d_2n(k) .

Taking limit as k → ∞, we get

d(Ax_2n(k), Ax_2m(k)-1 ) → ε and d(Ax_2n(k)+1, Ax_2m(k)-1) → ε.

Then,

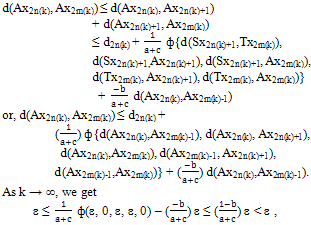a contradiction. Hence {Ax_n} is a Cauchy sequence in X and so by completeness of X, {Ax_n} converges to a point z ∈ X. Consequently the subsequences {Sx_2n+1} and {Tx_2n} of {Ax_n} also converge to z. Since {A, S} is compatible, we get

lim _n→∞(ASx_2n+1,SAx_2n+1) → 0

and therefore

lim _n→∞ASx_2n+1 lim _n→∞SAx_2n+1 = S(lim _n→∞ Ax_2n+1) = Sz.

Now we show that Sz = z. Suppose Sz ≠ z , then from (ii) we have ,

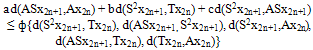In the limiting case, we get

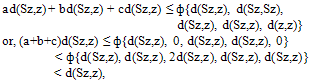a contradiction. Thus z is a fixed point of S. Similarly taking x = z and y = x_2n in (ii), we can show that z is a fixed point of A. Lastly we claim that z is a fixed point of T. Suppose it is not so, then

Since A is compatible with T we have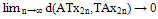

and so

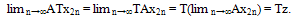Now from (ii), we have

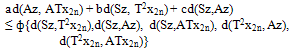As n → ∞, we get

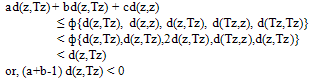a contradiction, since a+b > 1.

Therefore Tz = z. Thus z is a common fixed point of A,S and T. From (ii), we can easily show that the fixed point is unique. This completes the proof.

In that follows we give a common fixed point result for four self mappings satisfying a more general inequality condition. This in turn generalizes the fixed point result of Mukherjee[6].

2.2. Lemma (Kang et.al.[5]) :

Let (X,d) be a metric space, K ⊂ X and A, S : K → K be compatible mappings. If {x_n} is a sequence in K and

lim_n→∞ Ax_n = lim_n→∞ Sx_n = t for some t ∈ K,

then lim_n→∞ ASx_n = St if S is continuous.

2.3. Theorem II

Let (X,d) be a complete metric space and A,B,S and T be self mappings of X. Suppose that S and T are continuous. The mapping pairs {A,S} and {B,T} are compatible with A(X) ⊂ T(X) and B(X) ⊂ S(X) and there exists a upper semi continuous function ф:[0,∞) → [0,∞), which is non decreasing and

ф (t) < t for all t > 0. Let A,B,S and T satisfy the condition :

(vi) d(Sx,Ty) ≤ ф(max{d(Ax,By), d(Sx,Ax), d(Ty,By),

d(Ty,Bx), d(Sx,By), d(Ty,Ay)})

Then A, B, S and T have a unique common fixed point in X.

Proof: Since A(X) ⊂ T(X) and B(X) ⊂ S(X), we can choose a sequence {x_n} in X such that

Sx_2n = Bx_2n-1 and Tx_2n-1 = Ax_2n-2

for all n in the set N of all positive integers. Let

(vii) y_2n-1 = Tx_2n-1 = Ax_{2n -2} and y_2n = Sx_2n = Bx_2n-1 for n ∈ N

Now from (vi), we have

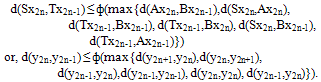Let d_2n = d(y_2n,y_2n+1) > 0 for all n = 0,1,2,… . Then we get

d_2n-1 ≤ ф (max{d_2n, d_2n, d_2n-1, 0, 0, d_2n-1}) = ф(d_2n) < d_2n.

Hence d_2n-1 < d_2n. Similarly we can show that d_2n< d_2n+1.

Therefore {d_n} is non decreasing sequence in R. We now show that {y_n} is a Cauchy sequence. Suppose that it is not so, then there exists an ε > 0 such that for any integer 2k, k = 0,1,2,… there exist two sequences {2m(k)}_k and {2n(k)}_k, k∈N with 2k < 2n(k) < 2m(k), for which

(viii) d(y_2n(k),y_2m(k)) > ε

If 2m(k) denote the smallest integer exceeding 2n(k)

satisfying (viii), we have

(ix) d(y_2n(k),y_2m(k)-2) ≤ ε

Then,

ε < d(y_2n(k), y_2m(k))) ≤ d(y_2n(k),y_2m(k)-2) +d_2m(k)-2 +d_2m(k)-1.

So by (ix) and as k → ∞, we get

(x) lim_k→∞d(y_2n(k), y_2m(k)) = ε

Now using (x) in the triangle inequalities

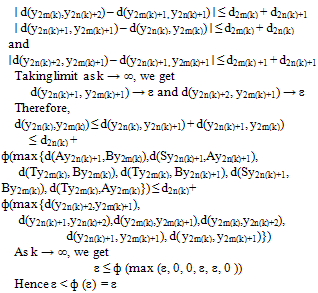a contradiction. Hence {y_n} is a Cauchy sequence in X. Suppose y_n → y ∈ X, then the subsequences {y_2n} and {y_2n-1} also converge to y. Since {A,S} and {B,T} are both compatible, it follows from the continuity of S and T that

(xi) Ty_2n-1 → Ty, By_2n-1 → Ty, Sy_2n → Sy, Ay_2n → Sy

Again from (vi), we get

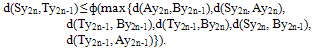By the upper semi continuity of ф and (xi), we get

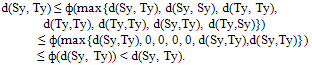This implies Sy =Ty. Similarly we can obtain that

(xii) Sy = By, Ty = Ay and so, Ay = By = Sy = Ty

Again from (vi), we have

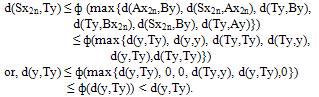Therefore y = Ty. Hence y = Ty = Ay = By = Sy. Thus y is the common fixed point of A, B, S and T.

To prove uniqueness let x (≠ y) be another common fixed point of A,B,S and T. Then from (vi), we get

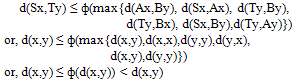and so, we get x = y. Thus A, B, S and T have a unique common fixed point y in X.

3. Conclusions

The inequality conditions (ii) and (vi) of our respective results are more general by involving a ф function than the conditions (1), (2) and (3) of the results of Som[10], Taskovic[12] and that of Mukherjee[6]. Moreover the nature of the functions are more restricted due to compatibility and we get common fixed points for such mappings.