-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Mathematics and Statistics
p-ISSN: 2162-948X e-ISSN: 2162-8475
2011; 1(1): 8-16
doi: 10.5923/j.ajms.20110101.02
On Bicomplex Nets and their Confinements
Rajiv K. Srivastava , S. Singh
Department of Mathematics, Institute of Basic Science, Khandari Campus, Dr. B. R. Ambedkar University, Agra – 282 002, India
Correspondence to: Rajiv K. Srivastava , Department of Mathematics, Institute of Basic Science, Khandari Campus, Dr. B. R. Ambedkar University, Agra – 282 002, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We have initiated the study of nets with bicomplex entries. Due to the multi dimensionality of the bicomplex space there arise different types of tendencies called confinements. The bicomplex space equipped with real order topology as well as idempotent order topology exhibits interesting and challenging behaviour of nets. Different types of confinements have been characterized in terms of convergence of the component nets. In the final section, certain relations between bicomplex nets and their projection nets have been derived.
Keywords: Bicomplex Numbers, Order Topology, Bicomplex Net, Real Confinement, Idempotent Confinement, Projection Net
Cite this paper: Rajiv K. Srivastava , S. Singh , "On Bicomplex Nets and their Confinements", American Journal of Mathematics and Statistics, Vol. 1 No. 1, 2011, pp. 8-16. doi: 10.5923/j.ajms.20110101.02.
Article Outline
1. Introduction
- The symbols
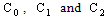 denote sets of real numbers, complex numbers and bicomplex numbers, respectively. A bicomplex number is defined as (cf.[1,2])
denote sets of real numbers, complex numbers and bicomplex numbers, respectively. A bicomplex number is defined as (cf.[1,2])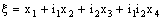 ,where
,where 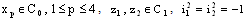 and
and 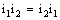 .With usual binary compositions,
.With usual binary compositions, 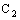 becomes a commutative algebra with identity. Besides the additive and multiplicative identities 0 and 1, there exist exactly two non-trivial idempotent elements denoted by
becomes a commutative algebra with identity. Besides the additive and multiplicative identities 0 and 1, there exist exactly two non-trivial idempotent elements denoted by 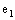 and
and 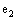 defined as
defined as 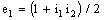 and
and 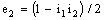 . Note that
. Note that 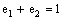 and
and 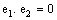 .A bicomplex number
.A bicomplex number 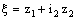 can be uniquely expressed as a complex combination of
can be uniquely expressed as a complex combination of 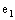 and
and 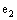 as (cf. [3])
as (cf. [3])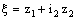
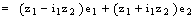
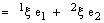 ,where
,where 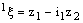 and
and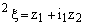 . The complex coefficients
. The complex coefficients 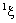 and
and 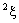 are called the idempotent components and the combination
are called the idempotent components and the combination 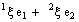 is known as idempotent representation of bicomplex number
is known as idempotent representation of bicomplex number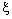 .The auxiliary complex spaces
.The auxiliary complex spaces 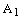 and
and 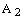 are defined as follows:
are defined as follows: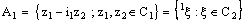 and
and 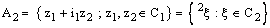 The idempotent representation
The idempotent representation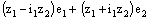
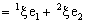 associates with each point
associates with each point 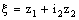 in
in , the points
, the points 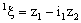 and
and 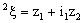 in
in 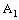 and
and 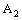 , respectively and to each pair of points
, respectively and to each pair of points 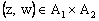 , there corresponds a unique bicomplex point
, there corresponds a unique bicomplex point 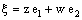 . Some updated details of the theory of Bicomplex Numbers can be found in [5,6].
. Some updated details of the theory of Bicomplex Numbers can be found in [5,6].2. Order Topologies on 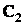
- Srivastava[3] initiated the topological study of
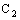 . He defined three topologies on
. He defined three topologies on 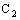 , viz., norm topology
, viz., norm topology 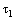 , complex topology
, complex topology 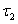 and idempotent topology
and idempotent topology 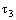 and has proved some results on these topological structures.Throughout, < denotes the ordering of real numbers and
and has proved some results on these topological structures.Throughout, < denotes the ordering of real numbers and 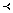 denotes the dictionary ordering of the complex numbers. Denote by
denotes the dictionary ordering of the complex numbers. Denote by 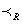 , the dictionary ordering of bicomplex numbers expressed in the real component form. The order topologies induced by this ordering will be called as Real Order Topology (cf.[4]), denoted by
, the dictionary ordering of bicomplex numbers expressed in the real component form. The order topologies induced by this ordering will be called as Real Order Topology (cf.[4]), denoted by 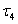 and is generated by the basis comprising of the members of the following families of subsets of
and is generated by the basis comprising of the members of the following families of subsets of 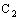 :
: 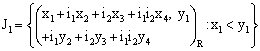
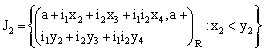
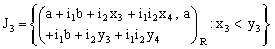
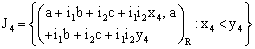 ,the set
,the set 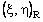 denoting the open interval with respect to the ordering
denoting the open interval with respect to the ordering 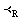 .Throughout the discussion, we shall consider some special types of subsets of the bicomplex space
.Throughout the discussion, we shall consider some special types of subsets of the bicomplex space 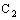 , equipped with real order topology.A set of the type
, equipped with real order topology.A set of the type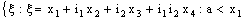 and
and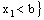 is called an open space segment. A set of the type {ξ: ξ = a + i1 x2 + i2 x3 + i1 i2 x4} is called a frame and is denoted as (
is called an open space segment. A set of the type {ξ: ξ = a + i1 x2 + i2 x3 + i1 i2 x4} is called a frame and is denoted as (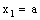 ). A set of the type {ξ: ξ = a + i1 x2 + i2 x3 + i1 i2 x4; b < x2 and x2 < c} is called an open frame segment. A set of the type {ξ: ξ = a + i1 b + i2 x3 + i1 i2 x4} is called as plane and is denoted as (
). A set of the type {ξ: ξ = a + i1 x2 + i2 x3 + i1 i2 x4; b < x2 and x2 < c} is called an open frame segment. A set of the type {ξ: ξ = a + i1 b + i2 x3 + i1 i2 x4} is called as plane and is denoted as (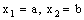 ). A set of the type
). A set of the type 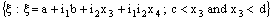 is called an open plane segment. A set of the type {ξ: ξ = a + i1 b + i2 c + i1i2 x4} is called as a line and is denoted as (
is called an open plane segment. A set of the type {ξ: ξ = a + i1 b + i2 c + i1i2 x4} is called as a line and is denoted as (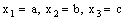 ). A set of the type {
). A set of the type {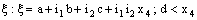 and
and 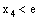 } is called an open line segment.Note that
} is called an open line segment.Note that 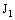 is a family of open space segments,
is a family of open space segments, 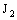 is a family of open frame segments,
is a family of open frame segments, 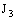 is a family of open plane segments and
is a family of open plane segments and 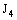 is a family of open line segments.Further, we shall consider some special types of subsets of the bicomplex space
is a family of open line segments.Further, we shall consider some special types of subsets of the bicomplex space 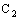 equipped with the idempotent order topology, (cf.[4]). Denote by
equipped with the idempotent order topology, (cf.[4]). Denote by 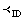 , the dictionary ordering of the bicomplex numbers expressed in the idempotent form. The order topology induced by this ordering is called as Idempotent Order Topology (cf.[4]). Hence, idempotent order topology,
, the dictionary ordering of the bicomplex numbers expressed in the idempotent form. The order topology induced by this ordering is called as Idempotent Order Topology (cf.[4]). Hence, idempotent order topology, 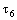 is generated by the basis
is generated by the basis 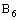 comprising of members of the following families of subsets of
comprising of members of the following families of subsets of 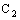 :
: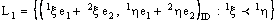
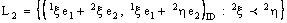 ,the set
,the set 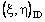 denoting the open interval with respect to the ordering
denoting the open interval with respect to the ordering 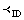 . A set of the type
. A set of the type 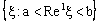 is called an open ID – space segment. A set of the type
is called an open ID – space segment. A set of the type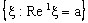 is called an ID – frame and is denoted as
is called an ID – frame and is denoted as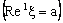 . A set of the type
. A set of the type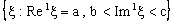 is called an open ID – frame segment. A set of the type
is called an open ID – frame segment. A set of the type 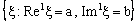 is called as an ID – plane and is denoted as
is called as an ID – plane and is denoted as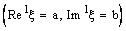 . A set of the type
. A set of the type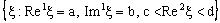 is called an open ID – plane segment. A set of the type
is called an open ID – plane segment. A set of the type 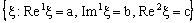 is called an ID – line and is denoted as
is called an ID – line and is denoted as 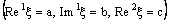 .A set of the type
.A set of the type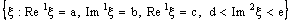 is called an open ID – line segment.
is called an open ID – line segment.2.1. Remark
- Note that,
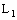 and
and 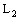 can also be described as
can also be described as 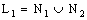 and
and 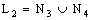 , where
, where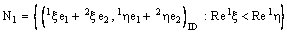
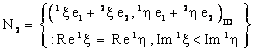
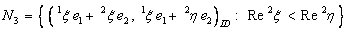
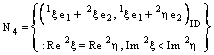 In other words,
In other words, 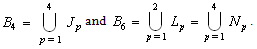
2.2. Remark
- The geometry of the Cartesian idempotent set determined by
 and
and 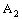 , i.e.,
, i.e., 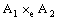 is entirely different from the geometry of Cartesian set determined by
is entirely different from the geometry of Cartesian set determined by 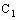 and
and 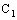 , i.e.,
, i.e., 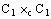 (for definitions see[3]). Obviously, the members of the families
(for definitions see[3]). Obviously, the members of the families 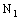 ,
, 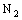 ,
, 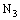 and
and 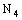 are open ID – space segments, open ID – frame segments, open ID – plane segments and open ID – line segments, respectively.
are open ID – space segments, open ID – frame segments, open ID – plane segments and open ID – line segments, respectively.3. Confinements of Bicomplex Nets in the Real Order Topology
3.1. Static and Eventually Static Bicomplex Net
- Let D be an arbitrary directed set. Then a bicomplex net can be defined as
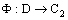 such that
such that 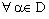
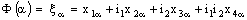
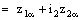
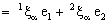 Further, a bicomplex net
Further, a bicomplex net  is said to be static on
is said to be static on  if
if 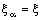 ,
, 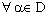 . It is said to be eventually static on
. It is said to be eventually static on 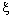 if there exists
if there exists 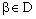 such that
such that 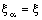 ,
, 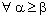 .
.3.2. Real Frame Confinement (RF Confinement)
- A bicomplex net
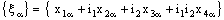 is said to be Real Frame confined (in short, RF confined) to the frame
is said to be Real Frame confined (in short, RF confined) to the frame 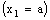 , if it eventually in every member of the family
, if it eventually in every member of the family 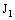 (of open space segments) containing the frame
(of open space segments) containing the frame 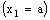 .
. 3.3. Real Plane Confinement (RP Confinement)
- A bicomplex net
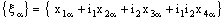 is said to be Real Plane confined (in short, RP confined) to the plane
is said to be Real Plane confined (in short, RP confined) to the plane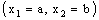 , if it is eventually in every member of the family
, if it is eventually in every member of the family 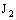 (of open frame segments) containing the plane
(of open frame segments) containing the plane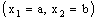 .
.3.4. Real Line Confinement (RL Confinement)
- A bicomplex net
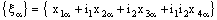 is said to be Real Line confined (in short, RL confined) to the line
is said to be Real Line confined (in short, RL confined) to the line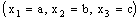 , if it is eventually in every member of the family
, if it is eventually in every member of the family 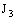 (of open plane segments) containing the line
(of open plane segments) containing the line 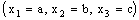 .
.3.5. Real Point Confinement (R – Point Confinement)
- A bicomplex net
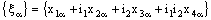 is said to be Real Point confined (in short, R – Point confined) to the bicomplex point
is said to be Real Point confined (in short, R – Point confined) to the bicomplex point 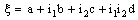 , if it is eventually in every member of the family
, if it is eventually in every member of the family 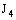 (of open line segments) containing the point
(of open line segments) containing the point 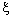 .
.3.6. Remark
- Note that if a bicomplex net
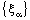 is RF confined to the frame
is RF confined to the frame 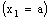 , it will not be eventually in any member of the family
, it will not be eventually in any member of the family 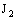 (and therefore will not be RP confined to any plane) unless
(and therefore will not be RP confined to any plane) unless 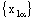 is eventually static on ‘a’ (and in this case,
is eventually static on ‘a’ (and in this case, 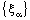 will be RP confined to the plane (
will be RP confined to the plane (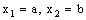 ) provided that
) provided that 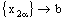 ). Similar cases will arise with the other types of bicomplex nets in the real form.
). Similar cases will arise with the other types of bicomplex nets in the real form. 3.7. Remark
- The R – Point confinement of a bicomplex net
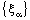 is a necessary but not sufficient condition for the convergence of the net in the classical sense (i.e., in the topology
is a necessary but not sufficient condition for the convergence of the net in the classical sense (i.e., in the topology 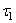 induced by the Euclidean norm). In fact, every eventually static net
induced by the Euclidean norm). In fact, every eventually static net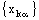 ,
,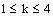 , converges and therefore, R – Point confinement of
, converges and therefore, R – Point confinement of 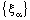 to
to 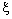 implies convergence of
implies convergence of 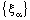 to
to 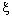 in the norm. To verify insufficiency, consider the bicomplex net
in the norm. To verify insufficiency, consider the bicomplex net 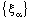 on the directed set
on the directed set 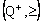 of positive rationals (with usual ordering) defined as follows:
of positive rationals (with usual ordering) defined as follows: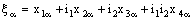 ,where
,where 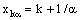 ,
, 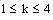 .The net converges to the point
.The net converges to the point 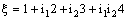 in the norm but not R – Point confined to
in the norm but not R – Point confined to 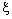 . As a matter of fact, no member of
. As a matter of fact, no member of 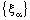 belongs to the line segment
belongs to the line segment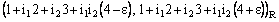 .
.3.8. Theorem
- A bicomplex net
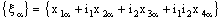 is RF confined to the frame (
is RF confined to the frame (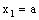 ) if and only if the net
) if and only if the net 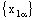 converges to a.Proof: Assume that
converges to a.Proof: Assume that 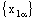 converges to a. Given
converges to a. Given 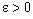 , let
, let 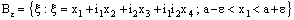 (3.1)be the member of
(3.1)be the member of 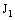 containing the frame
containing the frame 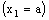 .Since,
.Since, 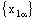 converges to a,
converges to a,  an index
an index 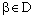 such that
such that 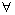
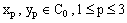 ,,
,,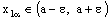 ,
, 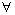
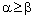
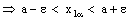 ,
, 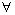
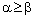
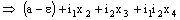
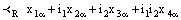 and
and 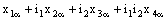
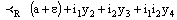
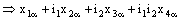
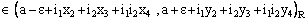
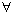
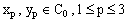 and
and 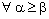 So that the net
So that the net 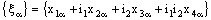 is eventually in
is eventually in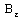 .Since
.Since 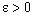 is arbitrary and every member of
is arbitrary and every member of 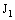 contains a
contains a 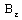 (for some
(for some 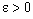 ),
), 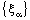 is RF confined to the frame
is RF confined to the frame 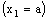 .Conversely, let the bicomplex net
.Conversely, let the bicomplex net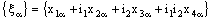 be RF confined to the frame
be RF confined to the frame 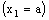 .Therefore, the bicomplex net
.Therefore, the bicomplex net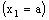 is eventually in every member of
is eventually in every member of 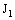 containing the frame
containing the frame 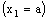 .In particular,
.In particular, 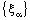 is eventually in
is eventually in 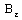 (
(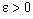 ) defined by (3.1).Thus,
) defined by (3.1).Thus, 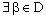 such that
such that 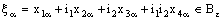 ,
, 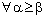
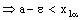
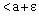 ,
, 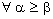
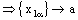 .Hence the theorem.
.Hence the theorem.3.9. Theorem
- A bicomplex net
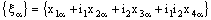 is RP confined to the plane
is RP confined to the plane 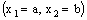 if and only if the net
if and only if the net 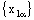 is eventually static on ‘a’ and net
is eventually static on ‘a’ and net 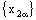 converges to ‘b’.Proof: Let the net
converges to ‘b’.Proof: Let the net 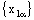 be eventually static on ‘a’ and the net
be eventually static on ‘a’ and the net 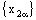 converge to ‘b’.Since
converge to ‘b’.Since 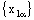 is eventually static on a,
is eventually static on a, 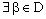 , such that
, such that 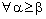 ,
, 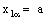 .Given
.Given 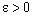 , let
, let 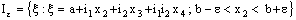 (3.2)be a member of
(3.2)be a member of 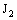 containing the plane
containing the plane 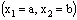 .As the net
.As the net 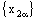 converges to b, there exists some
converges to b, there exists some 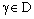 such that
such that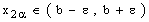 ,
, 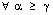 Since
Since 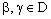 , there exists some
, there exists some 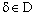 such that
such that 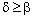 and
and 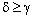 .Therefore,
.Therefore, 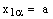 and
and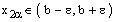 ,
,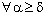 .
.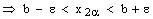 ,
, 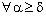
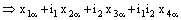
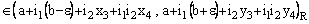 for any
for any 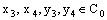 ,
, 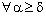 .So that the bicomplex net
.So that the bicomplex net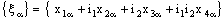 is eventually in
is eventually in 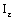 .Since
.Since 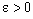 is arbitrary and every member of
is arbitrary and every member of 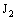 contains an
contains an 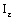 for some
for some 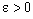 , the bicomplex net
, the bicomplex net 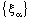 is RP confined to the plane
is RP confined to the plane 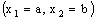 . Conversely, suppose that the bicomplex net
. Conversely, suppose that the bicomplex net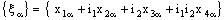 is RP confined to the plane
is RP confined to the plane 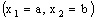 . Therefore, it is eventually in every member of the type
. Therefore, it is eventually in every member of the type 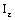 (
(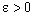 ) defined by (3.2), of the family
) defined by (3.2), of the family 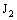 containing the plane
containing the plane 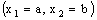 . So that for given
. So that for given 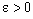 , there exists some
, there exists some 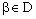 such that
such that 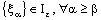
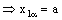 and
and 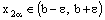 ,
, 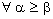 Therefore, the net
Therefore, the net 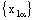 is eventually static on a and the net
is eventually static on a and the net 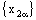 converges to b.On the similar lines, the following theorems can be proved.
converges to b.On the similar lines, the following theorems can be proved.3.10. Theorem
- A bicomplex net
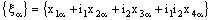 is RL confined to the line
is RL confined to the line 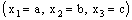 if and only if the nets
if and only if the nets 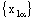 and
and 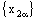 are eventually static on a and b, respectively and the net
are eventually static on a and b, respectively and the net 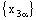 converges to c.
converges to c.3.11. Theorem
- A bicomplex net
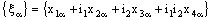 is R – Point confined to the bicomplex point
is R – Point confined to the bicomplex point 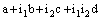 if and only if the nets
if and only if the nets 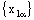 ,
, 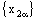 , and
, and 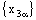 are eventually static on a, b and c, respectively and the net
are eventually static on a, b and c, respectively and the net 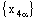 is converges to d.
is converges to d.3.12. Theorem
- (i) Every R – Point confined bicomplex net is RL confined. (ii) Every RL confined bicomplex net is RP confined.(iii) Every RP confined bicomplex net is RF confined. The converses of these implications are not true, in general.Proof: In fact, if a bicomplex net
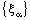 is R – Point confined to the bicomplex point
is R – Point confined to the bicomplex point 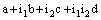 , then it is RL confined to the line
, then it is RL confined to the line 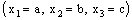 . Similarly, a bicomplex net which is RL confined to the line
. Similarly, a bicomplex net which is RL confined to the line 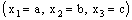 is RP confined to the plane
is RP confined to the plane 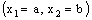 and a bicomplex net which is RP confined to the plane
and a bicomplex net which is RP confined to the plane 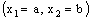 is RF confined to the frame(
is RF confined to the frame( 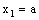 ).That the converse is not true, in general, is shown with the help of the two examples below.
).That the converse is not true, in general, is shown with the help of the two examples below.3.13. Example
- Consider the directed set
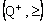 . Define the bicomplex net
. Define the bicomplex net 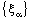 as follows:
as follows: 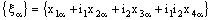 such that
such that 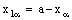 ,
, 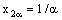 ,
, 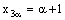 and
and 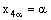 ,
, 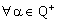 , where the net
, where the net 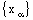 is eventually static on 0.Therefore, the net
is eventually static on 0.Therefore, the net 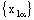 is eventually static on ‘a’ and the net
is eventually static on ‘a’ and the net 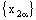 converges on ‘0’. So that the bicomplex net
converges on ‘0’. So that the bicomplex net 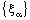 is RP confined to the plane
is RP confined to the plane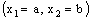 . Since, the net
. Since, the net 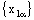 is eventually static on ‘a’. Therefore, the bicomplex net
is eventually static on ‘a’. Therefore, the bicomplex net 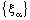 is eventually in every member of the family
is eventually in every member of the family 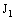 containing the frame
containing the frame 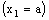 . Hence, the bicomplex net
. Hence, the bicomplex net 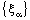 is RF confined to the frame
is RF confined to the frame 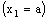 .
. 3.14. Example
- Consider the bicomplex net
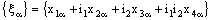 such that
such that 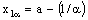 ,
, 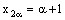 ,
, 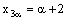 and
and 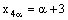 ,
, 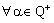 .This bicomplex net is RF confined to the frame
.This bicomplex net is RF confined to the frame 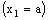 . The component net
. The component net 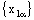 converges to ‘a’ but component net
converges to ‘a’ but component net 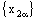 is not convergent. Therefore, the bicomplex net
is not convergent. Therefore, the bicomplex net 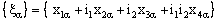 is not RP confined to any plane contained in the frame
is not RP confined to any plane contained in the frame 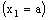 .
.4. Confinements of Bicomplex Nets in Idempotent Order Topology
- In this section, we assume to be furnished with the idempotent order topology (cf. [4]). Hence, the net
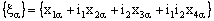 will be treated as the net
will be treated as the net 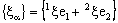 , where
, where 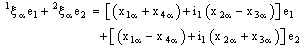 | (4.1) |
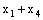 and
and 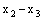 as
as 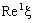 and
and 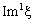 , respectively. Thus
, respectively. Thus 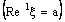 denote the frame
denote the frame 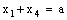 , whereas
, whereas 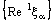 denote the net
denote the net 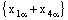 and so on. Under these notations, (4.1) can be rewritten as
and so on. Under these notations, (4.1) can be rewritten as 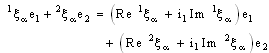 | (4.2) |
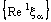 to be convergent, either both the nets
to be convergent, either both the nets 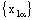 and
and 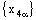 are convergent or both nets
are convergent or both nets 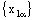 and
and 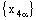 are divergent but
are divergent but 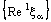 is convergent. Similarly, for net
is convergent. Similarly, for net 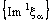 will be convergent if either both the nets
will be convergent if either both the nets 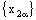 and
and 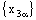 are convergent or both nets
are convergent or both nets 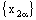 and
and 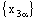 are divergent but
are divergent but 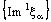 is convergent. The convergence of nets
is convergent. The convergence of nets 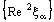 and
and 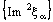 can be similarly interpreted.
can be similarly interpreted. 4.1. ID – Frame Confinement (ID – F Confinement)
- A bicomplex net
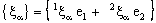 is said to be ID – Frame confined (in short, ID – F confined) to the ID – frame
is said to be ID – Frame confined (in short, ID – F confined) to the ID – frame 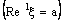 if it is eventually in every member of the family
if it is eventually in every member of the family 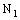 (of open ID – space segments) that contains the ID – frame
(of open ID – space segments) that contains the ID – frame  .
.4.2. ID – Plane Confinement (ID – P Confinement)
- A bicomplex net
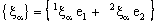 is said to be ID – Plane confined (in short, ID – P confined) to the ID – plane if it is eventually in every member of the family
is said to be ID – Plane confined (in short, ID – P confined) to the ID – plane if it is eventually in every member of the family 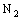 (of open ID – frame segments) that contains the ID – plane
(of open ID – frame segments) that contains the ID – plane 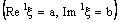 .
.4.3. ID – Line Confinement (ID – L Confinement)
- A bicomplex net
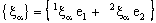 is said to be ID – Line confined (in short, ID – L confined) to the ID – line
is said to be ID – Line confined (in short, ID – L confined) to the ID – line 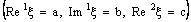 if it is eventually in every member of the family
if it is eventually in every member of the family 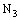 (of open ID – plane segments) containing the ID – line
(of open ID – plane segments) containing the ID – line 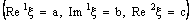 .
.4.4. ID – Point Confinement
- A bicomplex net
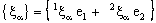 is said to be ID – Point confined to the point
is said to be ID – Point confined to the point 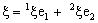 if it is eventually in every member of the family
if it is eventually in every member of the family 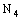 (of ID – line segments) containing the point
(of ID – line segments) containing the point 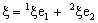 .
.4.5. Remark
- Note that if a bicomplex net
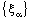 defined by (4.2) is ID – F confined to the frame
defined by (4.2) is ID – F confined to the frame 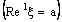 , it cannot be eventually in any member of the family
, it cannot be eventually in any member of the family 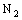 unless
unless 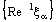 is eventually static on ‘a’. Similar cases will arise with the other types of the confinements of the bicomplex nets with respect to the idempotent order topology.
is eventually static on ‘a’. Similar cases will arise with the other types of the confinements of the bicomplex nets with respect to the idempotent order topology.4.6. Theorem
- A bicomplex net
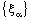 is ID – F confined to the ID – frame
is ID – F confined to the ID – frame 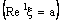 if and only if the net
if and only if the net 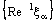 converges to a.Proof: Assume that
converges to a.Proof: Assume that 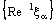 converges to a.Given
converges to a.Given 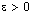 , let
, let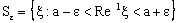 (4.3)be a member of containing the ID – frame
(4.3)be a member of containing the ID – frame 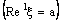 .Since
.Since 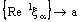 , there exists an index
, there exists an index 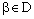 such that
such that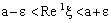 ,
, 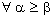 Hence, by the definition of
Hence, by the definition of 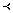 , we have
, we have 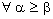 and
and 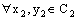 ,
,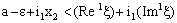 and
and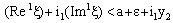 i.e,
i.e, 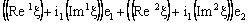
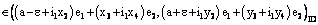 for any
for any 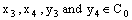 ,
, 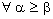 .So that the bicomplex net
.So that the bicomplex net 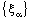 is eventually in
is eventually in 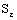 .Since
.Since 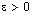 is arbitrary and every member of
is arbitrary and every member of 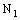 contains
contains 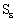 for some
for some 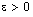 , by definition,
, by definition, 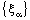 is ID – F confined to the ID – frame
is ID – F confined to the ID – frame 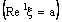 .Conversely, let the bicomplex net
.Conversely, let the bicomplex net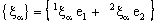 be ID – F confined to the ID – frame
be ID – F confined to the ID – frame 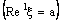 .By definition, it is eventually in every member of
.By definition, it is eventually in every member of 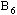 (in fact, of
(in fact, of 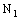 ) containing the frame
) containing the frame 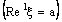 . In particular, it is eventually in
. In particular, it is eventually in 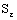 , for every ε, defined by (4.3).Thus,
, for every ε, defined by (4.3).Thus, 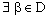 such that
such that 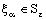 ,
,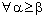 , i.e., such that
, i.e., such that 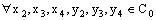 and
and 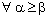
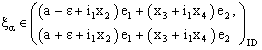 By definition of
By definition of 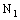 and
and 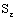 , we infer
, we infer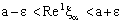
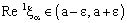 ,
, 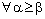
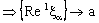 .Hence the theorem.
.Hence the theorem. 4.7. Theorem
- A bicomplex net
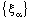 is ID – P confined to the ID – plane
is ID – P confined to the ID – plane 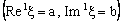 if and only if the net
if and only if the net 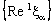 is eventually static on a and the net
is eventually static on a and the net 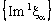 converges to b.Proof: Suppose that the net
converges to b.Proof: Suppose that the net 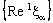 is eventually static at a and the net
is eventually static at a and the net 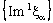 converges to b.Since the net
converges to b.Since the net 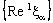 is eventually static on a,
is eventually static on a, 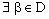 , such that
, such that 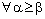 ,
, 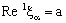 .Given
.Given 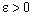 , let
, let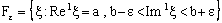 (4.4)be a member of
(4.4)be a member of 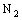 containing the ID – plane
containing the ID – plane 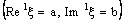 .Since the net
.Since the net 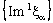 converges to b, there exists some
converges to b, there exists some 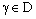 such that
such that 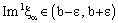 ,
, 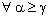 .Since
.Since 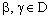 . Then, there exists some
. Then, there exists some 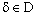 such that
such that 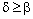 and
and 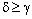 . Therefore,
. Therefore, 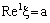 and
and 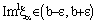 ,
,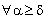 .
. 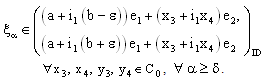 Therefore, the net
Therefore, the net 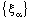 is eventually in
is eventually in 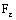 .Since
.Since 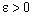 is arbitrary and every member of
is arbitrary and every member of 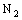 contains an
contains an 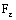 for some
for some 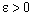 , by the definition, the bicomplex net
, by the definition, the bicomplex net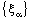 is ID – P confined to the ID – plane
is ID – P confined to the ID – plane 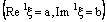 .Conversely, suppose that the bicomplex net
.Conversely, suppose that the bicomplex net 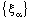 is ID – P confined to the ID – plane
is ID – P confined to the ID – plane 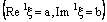 .Therefore, the bicomplex net
.Therefore, the bicomplex net 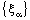 is eventually in every member of the family
is eventually in every member of the family  containing the ID – plane
containing the ID – plane  . In particular, the net is eventually in every open ID – frame segment
. In particular, the net is eventually in every open ID – frame segment 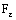 , (
, (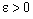 ), defined by (4.4) containing the ID – plane
), defined by (4.4) containing the ID – plane 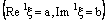 .Given
.Given 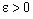 , there exists some
, there exists some 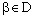 such that
such that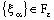 ,
, 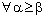 .Therefore, by definition of
.Therefore, by definition of 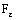 ,
, 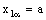 and
and 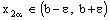 ,
, 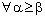
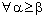 .Hence the theorem. On similar lines, the following theorems can be proved.
.Hence the theorem. On similar lines, the following theorems can be proved.4.8. Theorem
- A bicomplex net
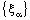 is ID – L confined to the ID – line
is ID – L confined to the ID – line 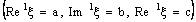 if the nets
if the nets 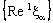 and
and 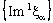 are eventually static on a and b, respectively and
are eventually static on a and b, respectively and 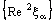 converges to c.
converges to c.4.9. Theorem
- A bicomplex net
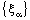 is ID – Point confined to the point
is ID – Point confined to the point 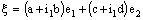 if the nets
if the nets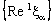 ,
, 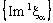 and
and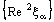 are eventually static on a, b and c, respectively and the net
are eventually static on a, b and c, respectively and the net 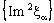 converges to d.
converges to d.4.10. Theorem
- (i) Every ID – Point confined bicomplex net is ID – L confined.(ii) Every ID – L confined bicomplex net ID – P confined.(iii) Every ID – P confined bicomplex net ID – F confined.The converses of these implications are not true, in general.Proof: In fact, if a bicomplex net
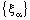 is ID – Point confined to the point
is ID – Point confined to the point 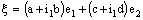 , say, then it is ID – L confined to the ID – line
, say, then it is ID – L confined to the ID – line 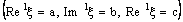 . Further, a bicomplex net which is ID – L confined to the ID – line
. Further, a bicomplex net which is ID – L confined to the ID – line 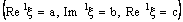 is ID – P confined to the ID – plane
is ID – P confined to the ID – plane 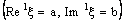 . Furthermore, a bicomplex net which is ID – P confined to the ID – plane
. Furthermore, a bicomplex net which is ID – P confined to the ID – plane 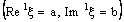 is ID – F confined to the ID – frame
is ID – F confined to the ID – frame 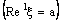 .To show that that the converse of these implications are not true, in general, we give below, in particular, an example of ID – F confined net which is also ID – P confined and an example of an ID – F confined net which is not ID – P confined.
.To show that that the converse of these implications are not true, in general, we give below, in particular, an example of ID – F confined net which is also ID – P confined and an example of an ID – F confined net which is not ID – P confined.4.11. Example
- Consider the directed set
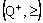 . Define the bicomplex net
. Define the bicomplex net 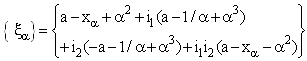 , where
, where 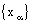 is eventually static on 0.By (4.1), the net
is eventually static on 0.By (4.1), the net 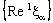 is eventually static on 2a and hence converges to 2a, the bicomplex net
is eventually static on 2a and hence converges to 2a, the bicomplex net 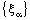 is eventually in every member of the family
is eventually in every member of the family 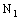 containing the ID – frame
containing the ID – frame 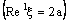 . Hence the net is ID – F confined to the frame
. Hence the net is ID – F confined to the frame 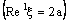 .Also, the net
.Also, the net 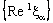 is eventually static on 2a and the net
is eventually static on 2a and the net 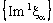 converges to 2a. Therefore, bicomplex net
converges to 2a. Therefore, bicomplex net 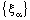 is ID – P confined to the ID – plane
is ID – P confined to the ID – plane 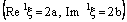 .
.4.12. Example
- Consider the bicomplex net
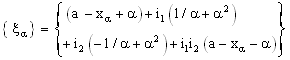 .By (4.1), the net
.By (4.1), the net 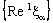 is eventually static on 2a and the net
is eventually static on 2a and the net 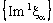 converges to 0. Therefore, the bicomplex net
converges to 0. Therefore, the bicomplex net 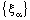 is ID – F confined to the ID – frame
is ID – F confined to the ID – frame 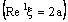 . Note that although the component net
. Note that although the component net 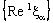 converges to 2a, it is not eventually static on 2a. Therefore, the bicomplex net
converges to 2a, it is not eventually static on 2a. Therefore, the bicomplex net 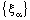 is not ID – P confined to any ID – plane contained in the ID – frame
is not ID – P confined to any ID – plane contained in the ID – frame 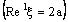 .
.5. Bicomplex Net and its Projection Nets
- This section is devoted to the study of relations between confinements of a bicomplex net and the convergence of its projection nets (cf.[7]) in the idempotent product topology (cf.[4]). Recall the definitions of the auxiliary complex spaces
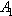 and
and 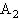 .
.5.1. Theorem
- A bicomplex net
 converges to a bicomplex point
converges to a bicomplex point 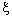 in the idempotent product topology if and only if the net
in the idempotent product topology if and only if the net 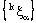 in
in 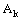 is confined to
is confined to 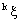 in (k = 1, 2).Proof: If
in (k = 1, 2).Proof: If 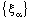 converges to the bicomplex point
converges to the bicomplex point 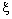 , it is eventually in every neighbourhood of
, it is eventually in every neighbourhood of 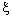 with respect to the idempotent product topology.Note that
with respect to the idempotent product topology.Note that 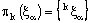 and the projections
and the projections 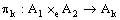 are continuous, k = 1, 2. (cf. [5]). Therefore, the net
are continuous, k = 1, 2. (cf. [5]). Therefore, the net 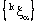 in
in 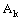 is eventually in every neighbourhood of
is eventually in every neighbourhood of 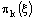 , k = 1, 2.Hence the net
, k = 1, 2.Hence the net 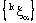 in
in 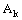 is confined to
is confined to 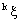 in
in 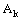 , k = 1, 2.The converse is straightforward.
, k = 1, 2.The converse is straightforward.5.2. Note
- The analogue of the above result is not true for any type of ID – confinement (except ID – Point confinement) of the bicomplex nets with respect to the idempotent order topology on
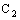 . Further, there is a characteristic difference between the convergence in the idempotent product topology and the confinement in the idempotent order topology in the sense that for any type of confinement (except ID – Point confinement) of a bicomplex net with respect to the idempotent order topology it is not necessary to have all the component nets to be convergent. We prove the following results in this context.
. Further, there is a characteristic difference between the convergence in the idempotent product topology and the confinement in the idempotent order topology in the sense that for any type of confinement (except ID – Point confinement) of a bicomplex net with respect to the idempotent order topology it is not necessary to have all the component nets to be convergent. We prove the following results in this context.5.3. Theorem
- If the bicomplex net
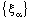 is ID – F confined to the ID – frame
is ID – F confined to the ID – frame 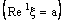 , the projection net
, the projection net 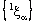 in is confined to the line in .Proof: Suppose that the bicomplex net
in is confined to the line in .Proof: Suppose that the bicomplex net 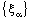 defined by (4.2), is ID – F confined to the ID – frame
defined by (4.2), is ID – F confined to the ID – frame 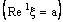 . Therefore the bicomplex net is eventually in every member of the family
. Therefore the bicomplex net is eventually in every member of the family 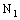 (of open ID – space segments) containing the ID – frame
(of open ID – space segments) containing the ID – frame 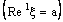 .Now, the projection of every member of
.Now, the projection of every member of 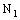 on
on 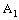 is a plane segment in
is a plane segment in 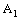 and therefore is a basis element of the dictionary order topology on
and therefore is a basis element of the dictionary order topology on 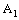 . Hence, the projection net
. Hence, the projection net 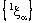 is eventually in every basis element of the dictionary order topology on
is eventually in every basis element of the dictionary order topology on 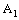 containing the line segment
containing the line segment 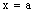 in
in 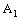 .Hence the net
.Hence the net 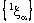 is confined to the line segment
is confined to the line segment 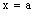 in
in 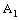 .
. 5.4. Theorem
- If the bicomplex net
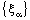 is ID – P confined to the ID – plane
is ID – P confined to the ID – plane 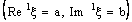 , the projection net
, the projection net 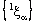 is confined to the point
is confined to the point 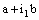 in
in 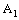 .Proof: Suppose that the bicomplex net
.Proof: Suppose that the bicomplex net 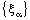 defined by (4.2), is ID – P confined to the ID – plane
defined by (4.2), is ID – P confined to the ID – plane 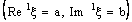 .Therefore, the bicomplex net
.Therefore, the bicomplex net 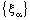 is eventually in every member of the family
is eventually in every member of the family 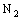 (of open ID – frame segments) containing the ID – plane
(of open ID – frame segments) containing the ID – plane 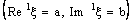 .Note that the projection of every member of
.Note that the projection of every member of 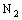 on the auxiliary space
on the auxiliary space 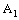 is a basis element (in fact, an open interval) of the dictionary order topology on
is a basis element (in fact, an open interval) of the dictionary order topology on 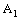 containing the point
containing the point 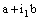 .So the projection net
.So the projection net 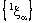 is eventually in every basis element of dictionary order topology on the auxiliary complex space
is eventually in every basis element of dictionary order topology on the auxiliary complex space 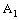 containing the point
containing the point 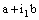 .Therefore, the projection net
.Therefore, the projection net 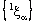 is confined to the point
is confined to the point 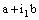 in
in 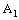 .
.5.5. Theorem
- If the bicomplex net
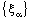 is ID – L confined to the ID – line
is ID – L confined to the ID – line 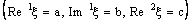 , the projection net
, the projection net 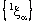 converges to the point
converges to the point 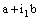 in
in 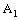 and the projection net
and the projection net 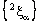 is confined to the line
is confined to the line 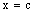 in
in 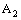 .Proof: Let the bicomplex net
.Proof: Let the bicomplex net 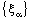 defined by (4.2), be ID – L confined to the ID – line
defined by (4.2), be ID – L confined to the ID – line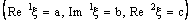 .Therefore, the bicomplex net
.Therefore, the bicomplex net  is eventually in every member of the family
is eventually in every member of the family  (of open ID – plane segments) containing the ID – line
(of open ID – plane segments) containing the ID – line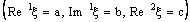 .Since the projection of every member of
.Since the projection of every member of 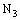 on
on 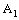 is a point
is a point 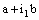 .Therefore, the projection net
.Therefore, the projection net 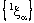 in
in 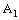 is eventually static on
is eventually static on 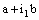 in
in 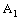 , so it is convergent to the point
, so it is convergent to the point 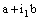 in
in 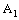 .The projection on
.The projection on 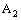 of every member of
of every member of 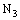 (of open ID – plane segments) is a plane segment in
(of open ID – plane segments) is a plane segment in 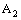 , which is a basis element of the dictionary order topology on
, which is a basis element of the dictionary order topology on 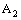 .Therefore, the projection net
.Therefore, the projection net 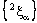 in
in 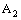 is eventually in every basis element of the dictionary order topology on
is eventually in every basis element of the dictionary order topology on 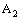 containing the line
containing the line 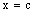 in
in 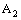 . Hence, the projection net
. Hence, the projection net 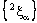 in
in 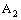 is confined to the line
is confined to the line 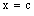 in
in 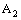 .
.5.6. Theorem
- If the bicomplex net
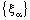 is ID – Point confined to the bicomplex point
is ID – Point confined to the bicomplex point 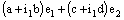 , the projection net
, the projection net 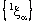 in
in 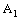 converge to the point
converge to the point 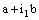 in and the projection net
in and the projection net 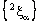 in
in 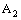 converge to the point
converge to the point 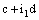 in
in 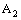 .Proof: Let the bicomplex net
.Proof: Let the bicomplex net 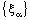 defined by (4.2), be ID – Point confined to the bicomplex point
defined by (4.2), be ID – Point confined to the bicomplex point 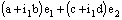 .Therefore, it is eventually in every member of the family (of open ID – line segments) containing the point
.Therefore, it is eventually in every member of the family (of open ID – line segments) containing the point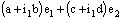 . So that the projection net
. So that the projection net 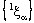 in is confined to the point
in is confined to the point 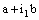 in
in 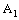 and the projection net
and the projection net 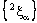 in
in 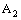 is confined to the point
is confined to the point 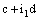 in
in 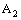 .
.5.7. Example
- Consider the bicomplex net
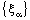 of Example 4.11.The net
of Example 4.11.The net 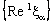 converges to 2a and the net
converges to 2a and the net 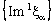 converges to 2a. However, the nets
converges to 2a. However, the nets 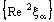 and
and 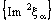 are not convergent and hence the projection net
are not convergent and hence the projection net 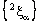 in
in 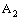 is not confined in
is not confined in 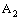 . So the bicomplex net
. So the bicomplex net 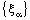 does not converge in the idempotent product topology.But the projection net
does not converge in the idempotent product topology.But the projection net 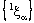 in
in 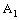 is confined to the point
is confined to the point 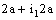 in
in 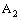 . Hence the bicomplex net is ID – P confined to the ID – plane
. Hence the bicomplex net is ID – P confined to the ID – plane 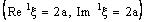 .
.5.8. Example
- Consider the directed net
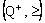 . Define a bicomplex net
. Define a bicomplex net 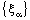 as follows:
as follows: 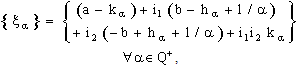
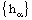 and
and 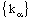 being eventually static on 0.The projection net
being eventually static on 0.The projection net 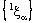 in
in 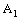 is confined to the point
is confined to the point 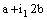 in
in 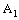 and the projection net
and the projection net 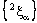 in is confined to the point
in is confined to the point 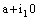 in
in 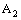 . Therefore, the bicomplex net is ID – Point confined to the point
. Therefore, the bicomplex net is ID – Point confined to the point 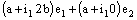 . Since, all the component nets are convergent. Therefore, the bicomplex net converges to the point
. Since, all the component nets are convergent. Therefore, the bicomplex net converges to the point 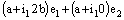 in the classical sense.
in the classical sense. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML