1. Introduction

The classical Vehicle Routing Problem (VRP) is NP-hard optimization problems and its objective is to minimize the total travelling cost, time, and distance with a vehicle, starting and ending its route at the depot while satisfying the various suppliers demands d [1]. In the literature, a number of variants of classical VRP have been studied, for example, the Multi Vehicle Routing Problem (MVRP) in which customers are to be served by a number of vehicles [2] and the Dynamic Vehicle Routing Problem (DVRP) where new suppliers orders arrive during the performance of the planned earlier work day, thus, routes must be reconfigured dynamically [3]. Another variant is the Capacitated Vehicle Routing Problem (CVRP) where the total demand of each route does not exceed the capacity of the vehicle [4] and the Vehicle Routing Problem with Time Windows (VRPTW), where the service at any suppliers starts within a given time interval, called a time window and a penalty is added if vehicle arrives after the upper bound of its time window while the arrival before the lower limit of the time window causes additional waiting time [5]. Another variant is the Vehicle Routing Problem with Simultaneous Pickups and Deliveries (VRPSPD) the customers will require a delivery or pickup service, but not both and only a single depot can receive and supply the loads while [6]. In today’s practical business environment, production and inventory processes are dependent on more advanced variants of the traditional VRP [7] such as The Multi Vehicle Routing Problem With Heterogeneous vehicle (MVRPWH) [8] and The MVRPWH and a Soft Time Windows [9] which are multiple delivery vehicles profiles with various features (volume, capacity, consumption) to service a pre-specified set of suppliers with known delivery demands from a central depot and the choice of the vehicle has a direct impact on the cost calculation [8,9].

Heuristic approaches such as Tabu Search (TS), Simulated Annealing (SA), Genetic Algorithm (GA), Particle Swarm Optimization PSO and Ant Colony Optimization (ACO) have been previously used in solving the VRP and all its variants are [10], however, it was stated that hybridization of heuristics methods gives more promising result than utilization of a unique heuristic approach [11]. For example, TS is combined with GA mutation operator and local search tactics and is applied in VRP [12] and SA is combined with GA crossover operator to is applied in CVRP [13]. Also, PSO was combined with Variable Neighborhood Descent algorithm (VND) in solving VRPSPD [14], the Unified Hybrid Genetic Search (UHGS) was combined with the 2-opt and 3-opt local search techniques in solving CVRP [15], while GA was combined with the cheapest insertion method in solving VRPSPD [16]. ACO was combined with K-means and crossover operation in solving DVRP [17], and with nearest neighbour search methodin solving VRPTW with multiple depot [18]. In solving CVRP, GA was introduced to enhance ACO performance by adjusting pheromone matrix [19] or to increase local search capability [20]. As it is necessary to compromise between the exploration (global search ) and exploitation (local search) in any hybrid heuristic model [21], where exploration pushes towards much more promising areas of the search space, while exploitation aims to avoid being locked up in local minima [22]. Thus, we introduce our new proposed GA/ACO hybrid model to make use of both the evolutionary effect of GA representing local searching capability and the cooperative effect and feedback mechanism of ACO representing global searching capability. To do so, after each iteration, the best performance individual in GA is subjected to ACO while the worst performance individuals in GA are replaced by best performance ants in ACO leading to extensively exploring the search space and avoiding the trapping into prematurely local minimum. This paper is organized as follows, in section II the mathematical model of the MVRPWH and a Soft Time Windows is reviewed and in section III we present our proposed algorithm, and finally the experimental results comparing our proposed model with the GA used in [9] is done.

2. Mathematical Model

The objective of the MVRPWH and a Soft Time is based on the following characteristics

1. The decision model considers multiple periods, multiple suppliers, and multiple vehicles.

2. The depot is both the shipping point and the final destination of each vehicle.

3. The distance and travelling time between each two suppliers are fixed and known.

4. Different types of vehicles have different unit travelling costs.

5. The unloading time in each supplier is fixed and known.

6. The assigning cost for each vehicle is fixed and known and different assigning costs occur for different types of vehicles.

7. Each vehicle has a limited loading capacity and different types of vehicles have different loading capacities.

8. Each vehicle has a limited travelling distance in a period and different types of vehicles have different travelling distance limits.

9. Each supplier has a soft time window and if a vehicle arrives to a supplier after the latest soft time, a tardiness cost will be charged by the supplier based on the tardiness time.

10. Multiple vehicles can be used in a period and any supplier can be visited by only one vehicle in any period.

11. No shortage of outsourced materials is allowed.

The objective function is to minimize the total transportation cost including the assignment cost for assigning vehicles, the travelling costs among the suppliers, and the tardiness cost when a vehicle arrives a supplier late and the mathematical model can be written as follows:

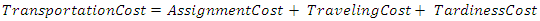(1)

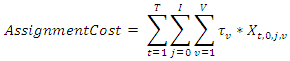(2)

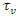where is the fixed cost for assigned vehicle 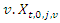is a binary variable equals one if vehicle 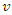departs from the depot 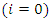to supplier 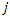in period 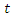and 0 otherwise..

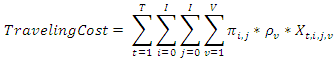(3)

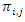Where is the travelling distance from supplier 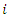to supplier 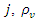is the travelling cost per unit of distance for vehicle 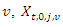is a binary variable equals one if vehicle 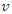departs from the supplier 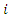to supplier 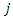in period 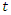and 0 otherwise.

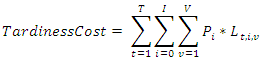(4)

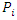Where is the tardiness cost per unit of time for the supplier 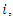and 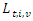is the tardiness time in period 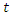of vehicle 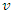when arriving at supplier

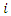Subject to the following conditions

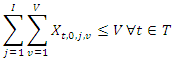(5)

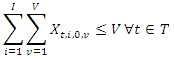(6)

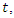These two constraints ensure that at any period any vehicle 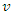should depart from the depot (node 0) and return to the depot

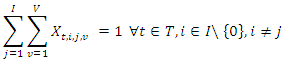(7)

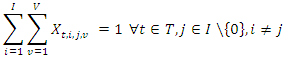(8)

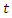These two constraints ensure that at any period only one vehicle 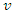leaves from only one supplier 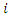and enters to another one supplier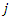

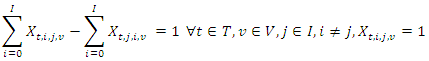(9)

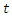This constraint ensures that at any period , if any vehicle 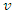leaves from supplier 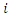to another supplier 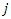, it should not return back form supplier 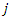to supplier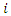

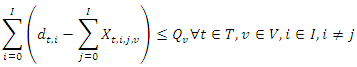(10)

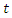This constraint ensures that at at any period , the total demand of all suppliers 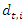visited by any vehicle 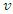should be less than or equal to the vehicle's maximum loading size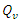

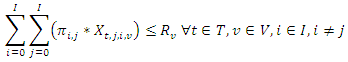(11)

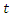This constraint ensures that at any period , for any vehicle 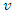, the total travelling distance 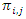should be less than or equal to the vehicle's maximum travelling distance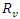

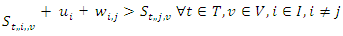(12)

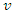This constraint ensures that for any vehicle visits supplier 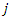after supplier 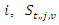the service start time for supplier 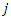should start after 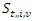the service start time for supplier 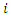plus 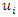the unload time at supplier 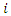and 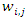the travelling time from supplier i to supplier .

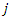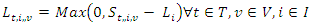(13)

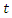This constraint ensures that at any period for any vehicle 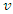arriving at supplier 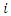, the tardiness time exist if 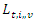the service start time 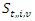is higher than the maximum allowable start time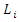

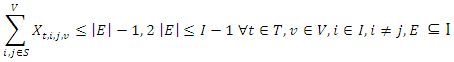(14)

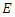This ensures the elimination of any sub-tour within the main tour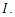

3. Proposed Hybrid GA/ACO

The balancing between exploration (global search) and exploitation (local search) is necessary to adequately searching the whole search space without being trapped in a local minimal where exploration is the process of visiting entirely new regions of a search space, whilst exploitation is the process of visiting those regions of a search space within the neighborhood of previously visited points [21]. In the literature, there are three different forms of GA/ACO hybridization, first GA is a global search while ant ACO is a local search [22], second GA is used to adapt ACO parameters [23], and finally, GA concepts is incorporated into ACO to enhance its performance [24]. In our research, we adopt a new strategy by considering the GA as a local search and ACO as a global search, to ensure the compromise between the GA local search (exploitation) capability and ACO global search (exploration) capability The three heuristic algorithms: Genetic Algorithm (GA), Ant Colony Optimization (ACO), and our proposed hybrid (GA/ACO) are introduced below.

A. Genetic Algorithm (GA)

Genetic Algorithm (GA) was first introduced by Holland is an evolutionary based searching approach based on the process of natural evolution and the idea of survival of the fittest [25]. GA is started with a set of solutions (population) and move from one generation to a new one according to their fatness, and this process is repeated until certain conditions are satisfied. GA algorithm can be outlined in the following steps [25].

1. (Start) Generate random solution (population) in the first generation.

2. (Fitness) Evaluate the fitness of each chromosome x in the population.

3. (New population) Create a new population by repeating the following steps until the new population is complete.

a. (Selection) Select two parent chromosomes from a population according to their fitness and as fitness increases, probability of acceptance increases.

b. (Crossover) with a crossover probability cross-over the parents to form a new offspring (children). If no crossover was performed, offspring is an exact copy of parents.

c. (Mutation) new offspring will be mutated according to a pre specified mutation probability.

d. (Replace) new offspring are used to form a new population in the next generation 4.

4. (Test) if the end condition is satisfied, stops, and returns the best solution in current population.

5. (Loop) Go to step 2.

B. Ant Colony Optimization (ACO)

Ant Colony Optimization ACO was first introduced by Macro Dorigois a population bases searching approach based on the behavior of ants. The ants always stay in their colonies and work in groups and explore many paths to find the shortest path to reach the food. Initially, ants randomly move around their surrounding and lay some sort of chemical on the ground which is known as Pheromone. When an ant finds the food it goes back to its nest by filling the ground again with that pheromone trails, thus, other ants know which path to follow [26]. ACO incorporates three important processes, first the solution construction when ants move through their surrounding, second, pheromone density update, and finally the centralized actions to improve obtained solution based on mutual cooperation between ants via exchanging information according to the following equations [26].

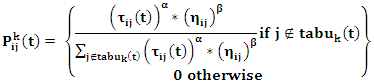(15)

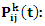Where the probability that ant 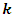will move from position 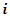to position 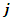at iteration 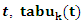is the tabuset of already visited positions by ant 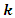at iteration 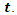if the position 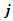has been set to be visited, it is removed from the 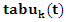and the. The last remaining index remaining is the last visited position. 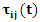is the pheromone density of the connection 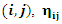is the visibility of the connection 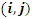and 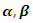are the relative influence of the pheromone trails and the visibility values, respectively. At the end of each iteration, 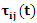is updated according to the following equation [23,26].

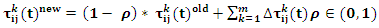(16)

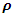Where is the pheromone evaporation rate to adjust the speed of convergence and it takes on positive values from 0 to 1. 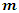is the number of ants (solutions), and 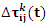is the increased pheromone of link in ant Ant weight strategy is used in updating pheromone by the following equation [24]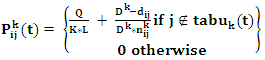

(17)

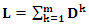(18)

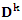Where is the fitness (length) of the ant (solution) number 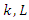is the sum of lengths of all solutions, 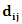is the length of the connection 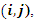and 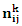is the connection order in the ant number

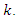C. Hybridization of GA and ACO

As GA is evolutionary based searching algorithm, so it is capable of effectively performing the exploitation due to mutation, crossover, and reproduction processes but it is not capable in properly performing the exploration due to leakage of population diversity [27]. On the other hand, as ACO is a population based searching algorithm so it is capable of effectively performing the exploration due to mutual feedback cooperative information between ants, but it is not adequate for exploitation due to leakage of local search capability [28].

In our proposed GA/ACO algorithm, after each GA iteration, the best performance individual is subjected to ACO to ensure that it is not trapped in a local minima, if a new better solution is found after applying ACO, so it emphasize that the GA old best solution was trapped in a local minima. Also the worst performance GA individuals is replaced by the best performance ACO ants to increase the diversity in the search space and avoid being restricted in regions that couldn't achieve any improvement in finding new regions with better solutions and our algorithm is done by the following steps

1 - At any new generation 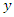for any individual 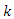in the population calculate its fitness function 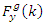and the best GA fitness individual 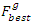is decided according to:

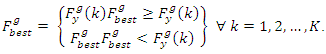(19)

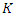Where is the number of individual in the GA population.

2 - The individuals in the GA population will be sorted according to their fitness to construct a new modified GA population where the first individual in the new modified population has the best fitness in the original population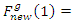

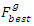3 – The new modified population will be divided into two portions, the first is the discarded portion (L*Ψ) containing the worst individuals' fitness function who will be discarded in the next generation where Ψ is the arbitrary selected breeding ratio between zero and one and the other (L*(1-Ψ)) individuals will continue in the next generation [29].

4 - The best fitness individual 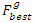will be the ant representing the initial solution to the ACO

5 – As done in GA, for any ant 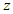in the colony calculate its fitness function 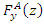and the best ACO fitness ant 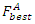is decided according to:

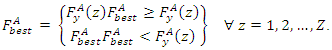(20)

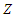Where is the number of ants in the ACO colony.

6 – As done in GA, The ants in the ACO colony will be sorted according to their fitness to construct a new modified ACO colony where the first ant in the new modified colony has the best fitness in the original population

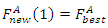7 – The minimum of the best GA fitness individual 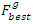and the best ACO fitness ant 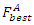is selected to be the best GA fitness individual 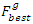for the new generation

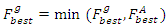(21)

8 – The first (L*Ψ) ants in the new modified ACO colony will replace the discarded individuals in the new modified GA population

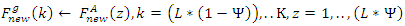(22)

9 – After replacement, the new modified GA population will replace the original GA population for the next generation

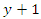
4. Results and Discussion

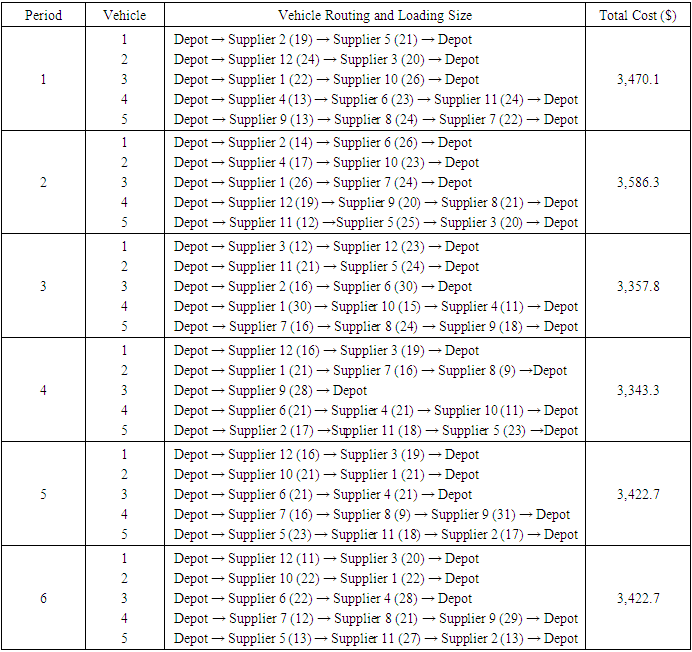
The case study is based on a manufacturer in the food industry [9] where there are one manufacturer, 12 suppliers, and 5 vehicles and the objective is to minimize the total transportation cost using the software packages MATLAB 2015 (The MathWorks, Inc., Natick, MA, USA) is used [30]. 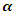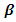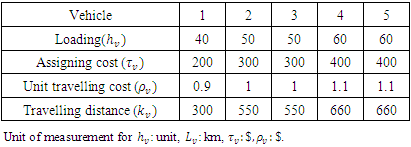For GA, the population size is 150, the mutation rate is 0.15, the crossover rate is 0.85, and the generation number is 1000 as selected in the original experiment [9] and for ACO, for simplicity, the arbitrary selected constants, is 1, is 2, and 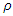is 0.5 as stated in [24] and Ψ is selected to be 0.1 as it was firstly introduced in [29] Table 1 shows the fixed cost for assigning a vehicle, loading and travelling distance limits of each vehicle, and the travelling cost per distance unit [9]. 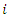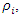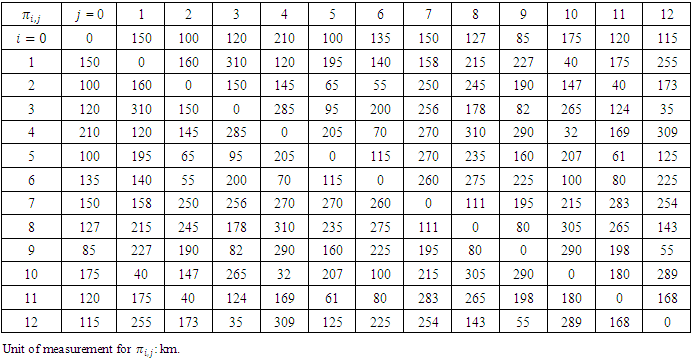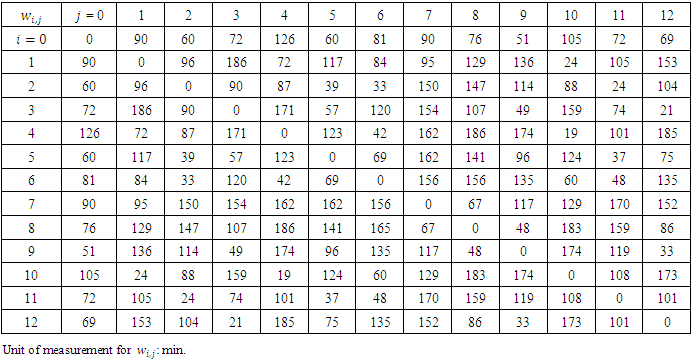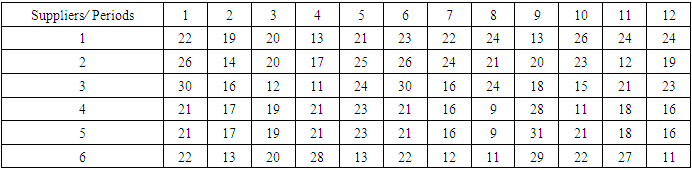Table 2 shows the data of all suppliers which are, the unload time (in minutes) required at supplier , the tardiness cost per minute charged by supplier loading and travelling distance limits of each vehicle when a vehicle arrives after the latest soft time and is the latest soft time (in minutes) to start the service at the supplier 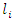[9]. Table 3 and Table 4 show the travelling distance the required travelling time between all suppliersand the depot [9] and there are 6 periods and the suppliers demand during these periods are shown in Table 5 [9].

Table 1. Vehicles Assignment, limits, and travelling cost [9]

Table 2. Suppliers data [9]

Table 3. Travelling distance symmetric matrix among suppliers [9]

Table 4. Travelling time symmetric matrix among suppliers [9]

Table 5. Suppliers demand during the periods [9]

The best solution obtained using both GA approach as mentioned in [9] and our proposed hybrid GA/ACO are shown in Table 6 and Table 7 respectively.

Table 6. Best solution obtained using GA [9]

Table 7. Best solution obtained using our proposed hybrid GA /aco

Comparing between these two above tables we can find the following

First: -Referring to Table 6 and Table 7, it is obvious that our hybrid proposed model gives lower cost than the standard GA model for all the six mentioned period indicating that our proposed model is better in searching the whole entire search space to find new regions with better performance which can not be found by the standard GA model.

Second: -Referring to Table 7 in period 4, its construction is based on using vehicle no. 3 in visiting only one supplier (supplier no. 9) which different from the constructions of all other periods in both tables where the first three vehicles visit two cities while the other two visit three cities. This proves that our proposed model can avoid trapping in a local minima leading to find new places in the search space with new better solutions which could not be achieved by the standard GA model.

Third: - Referring to Table 6 and Table 7 in periods 5&6, for Table 6 the cost function is the same although the vehicle routing is different in the two periods while for Table 7 both the cost function and vehicle routing are identical. It provides that the standard GA model can easily trapped in many local minima due to its leakage in making the necessary compromise between local search and global search while our proposed model can avoid this trapping and reach the regions with better solutions due to its capability in making this compromise.

This comparison proves that our proposed GA/ACO can achieve the necessary balance between exploration and exploitation leading to better realizing of the objective function by reducing the cost.