Akintola K. G.1, Emmanuel J. A.2
1Department of Software Engineering, Federal University of Technology, Akure
2School of Science and Technology, United States International University-Africa, Nairobi, Kenya
Correspondence to: Akintola K. G., Department of Software Engineering, Federal University of Technology, Akure.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Hand gesture recognition has gotten so many areas of application such as in human-computer interaction, hearing impaired communication and systems control. Recognizing gestures in videos however is a challenging task. Many techniques and features have been adopted in the literature but some of the methods still need to be improved upon. There are basically two types of gestures: the static and the dynamic gestures. In this work, a computer vision-based system for recognition of static hand gesture is proposed using a fusion of the histogram of oriented gradient and the Hu invariant moments as features. The proposed system consists of three phases: preprocessing, feature extraction and classification. The images are first pre-processed using segmentation and morphological operations. The histogram of oriented gradient and the Hu invariant moments are then extracted as features. The extracted features are concatenated and passed as input into a multilayer neural network model to recognize the static hand gesture. The proposed system is implemented and tested on the hand gesture database collected online. The model was trained using 500 features which consist of 20 gestures each from 25 gesture types. The model is then tested with another 500 gestures which also consist of 20 gestures each from the 25 gesture types. The experimental results show that the proposed system is able to recognize the static gestures with accuracy of 96.4%.
Keywords:
Gesture, Static, Dynamic, HOG, Hu-Moments, Neural
Cite this paper: Akintola K. G., Emmanuel J. A., Static Hand Gesture Recognition Using Multi-Layer Neural Network Classifier on Hybrid of Features, American Journal of Intelligent Systems, Vol. 10 No. 1, 2020, pp. 1-7. doi: 10.5923/j.ajis.20201001.01.
1. Introduction
Gestures are usually understood as hand and body movement which can pass information from one to another (Liang and Ouhyoung, 1996). Ever since the creation of computers, the inventors and computer scientists have always been looking for efficient ways of interacting with the machine. Interaction with the first generation of computers can only be done by the trained engineers. As development proceeds in computer software and hardware, several improvements were achieved in convenient interaction with computers. The development of Window Icons, the mouse devices, the touch screen systems are a few examples of human–computer interaction. Recently, the research focus is on how we can interact with computers using hand gestures. This falls under the field of computer vision. The availability of hardware resources and algorithms developed in this field made venturing into the mode of interaction a reality. There are various areas of application of gesture recognition. These include games, machine control systems such as robots, impaired communication systems and sign language communication and so on. Gesture can be categorized into static gestures and dynamic gestures. A static gesture is particular hand pose defined by a single image while a dynamic gesture is a motion gesture that can be depicted by a sequence of successive images. Several works have been done in this area. Such include Rahman and Afrin (2013) who worked on hand gesture recognition using multi-class support vector machine. First edge images were extracted from the gesture images. Next randon transformations on the edge images were performed. The obtained results were then passed through a bi-orthogonal transformation to obtain the final features. The features are then passed through a multi-class SVM model for recognition. To test the model, ten hand gestures were performed by five users. The result obtained has 92% accuracy. The computation of the features can be computationally complex.Liu Yun et al. (2012) present a hand gesture recognition based on multi-feature fusion. The method extracts the Angle count, skin color angle, non-skin color angle from the hand shaped region. Also, the Hu invariant moment features are also extracted from the gesture contour. A template matching method is used to classify the features into the gesture class using Euclidean distance as a metric. In experiment performed on some testing images, an average recognition accuracy of 91% was achieved. Nagarajan and Subashini (2013) developed a static hand gesture recognition system for sign language alphabets using Edge Oriented Histogram and multi-class SVM. In his approach, edge images were first extracted from the gesture images using the Canny edge detector. Then, histogram features were extracted from the canny edge images. A support vector machine is developed to recognize the gestures. Nagashree et al. (2015) presents a hand gesture recognition using Support Vector Medicine. Here, Canny edge detection algorithm was used for edge detection and histogram of oriented gradients was used for feature extraction and SVM as classifier. Bamwend and ozerdem (2019) A kinect based hand gesture recognition is presented. A neural method and SVM was used to classify the Images acquired using Microsoft kinect. Features were extracted using the HOG. No author has considered the use of the fusion of the histogram oriented histogram and the Hu invariant moment features that is considered in this paper.
2. Proposed Static Hand Gesture Recognition System
Figure 1 shows the framework of the ANN-based system for gesture recognition. It consists of the Region of Gesture detection module, feature extraction module and the ANN model gesture recognition module.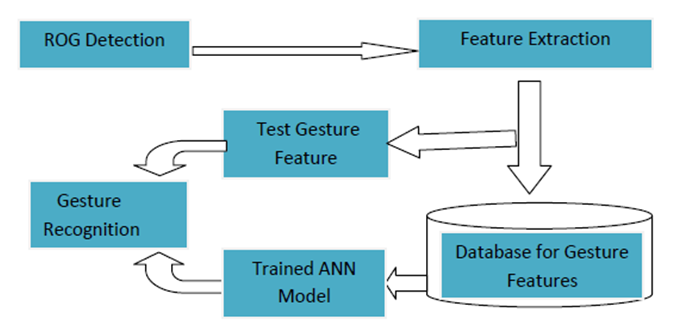 | Figure 1. Proposed Gesture Recognition Flow Diagram |
2.1. ROG Detection
The objective of the Region of Object Detection (ROG) segmentation is to extract the region of the hand gesture from the given image. The simple background subtraction technique as used in in Heikkila and Silven (1999) was adopted to segment the region of interest from the image background. Foreground pixels are identified by comparing each pixel value of the image is compared with a threshold. A pixel is marked as object region if the value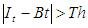 | (1) |
where Th is a predefined threshold and Bt is set to zero.Background subtraction techniques perform well but they are usually sensitive to dynamic changes for instance moved object, sudden illumination changes (Doulamis et al. 2010). Figure 2a shows some of the gesture images while Figure 2b shows the binarised image. Figure 2c shows the Region of Gesture extracted from Figure 2b.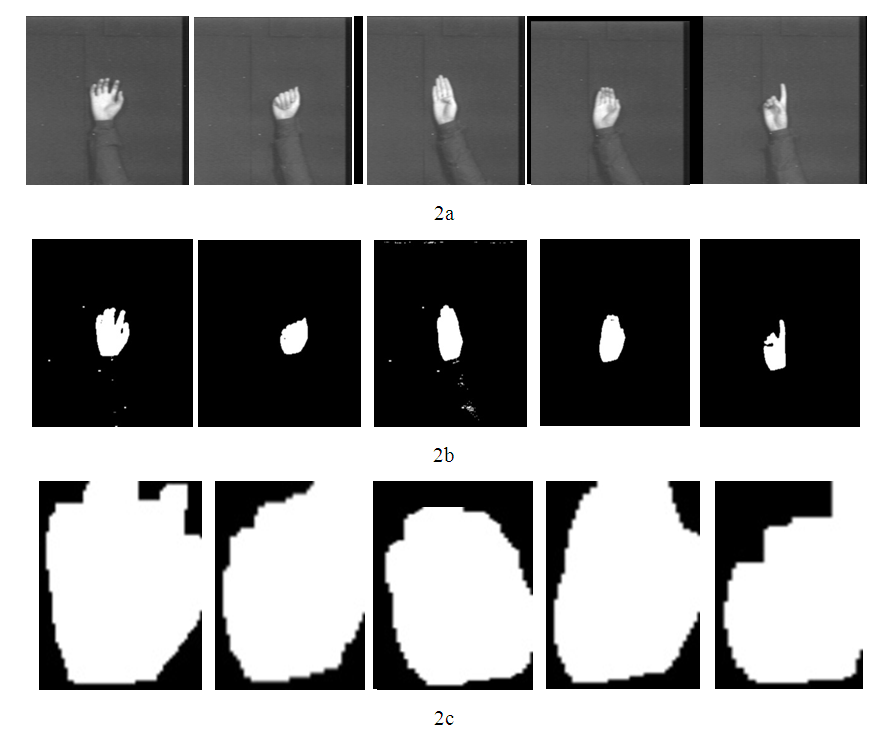 | Figure 2. a. Sample gesture images b. Binary Images of the gesture images c. Region of Gesture in the images in Figure 2b |
2.1.1. Morphological Filtering
The essence of the morphological filtering is to reduce noise from the binary image and to get a smooth, closed and complete hand gesture image (Ghosh and Ari, 2015). To remove noise from the image various morphological operations such as erosion and dilation are performed on the segmented image region (Nagarajan and Subashini 2013).
2.2. Feature Extraction
In this section, the process of extracting features from the segmented regions of the image is presented.a. Hu invariant moments.A feature can be defined as the unique characteristics extracted from an object that can be used to recognize such an object. The invariant moment theory was first proposed by Hu M.K. in 1962 (Yun et al. 2012). The moments were given in terms of functions which are translation, rotation and scale invariance. It consists of seven invariant moment expressions. The moments are extracted from the detected objects’ contour shown in Figure 2c. These features capture the shape information of the gestures. The computation of these features is given as follows (Yun et al. 2012):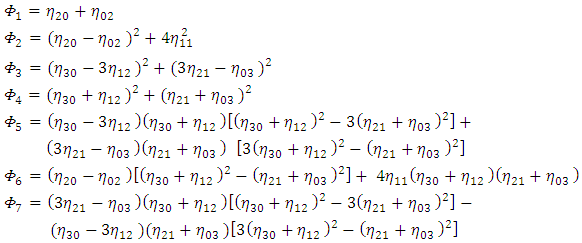 | (2) |
where 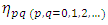 are the normalized central moments defined as:
are the normalized central moments defined as: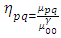 | (3) |
where 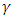 is given as:
is given as: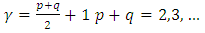 | (4) |
and 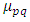 are the central moments calculated as follows:
are the central moments calculated as follows: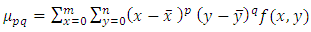 | (5) |
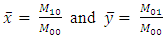 | (6) |
and 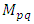 are the
are the 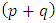 -th order moments:
-th order moments: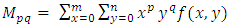 | (7) |
Figure 3 shows sample Hu invariant of the five gestures shown in Figure 2c. | Figure 3. Hu values extracted from gestures in Figure 2c |
b. Histogram of oriented Gradients The corresponding ROG was cut out from the grayscale image as shown in Figure 4. These images were used to compute the HOG features. Gradient computation is a critical stage in the descriptors computation. In this research, the Sobel operator is used. Given an image, I, the horizontal and vertical gradient of each pixel (x,y) are calculated as follows: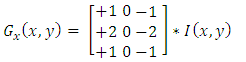 | (8) |
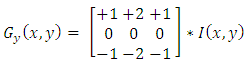 | (9) |
The magnitude of the gradient is calculated as follows: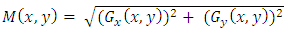 | (10) |
where 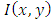 is the image.The gradient direction is computed as follows:
is the image.The gradient direction is computed as follows: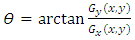 | (11) |
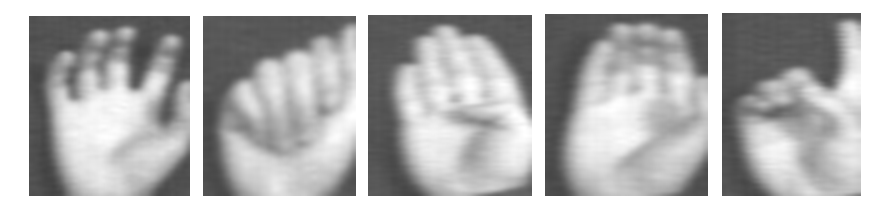 | Figure 4. ROG of five typical gestures from the database |
 | Figure 5. a. Grayscale Gesture Image b. Horizontal gradient Image, c. Vertical gradient Image, d. Gradient Norm Image and e. Gradient Direction Image for gestures 1 and 2 of figure 4. The gradient momentum and gradient direction are used to compute the Histogram of Oriented Gradient (HOG) of the gestures (Bamwend J., Özerdem M.S., 2019). Sample HOG extracted from Figure 5 are shown in Figure 6 |
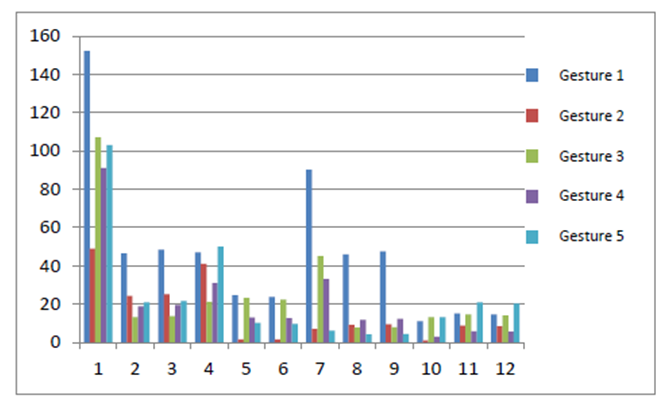 | Figure 6. HOG of the five gesture images segmented in figure 1 above |
2.3. Design of the Neural Network Model for Gesture Classification
Artificial Neural Network (ANN) is a widely used pattern-recognition methodology for machine learning. It emulates biological neural network with several interconnected neurons, however, ANN only utilizes a very limited set of concepts from its biological counterpart with one or more layer of neurons, which are fully or partially connected. Each connection between two nodes has a weight, which encapsulate the “knowledge” of the system. By processing existing cases with inputs and expected outputs, existing weights would be adjusted based on differences between actual and expected outputs. The general ANN learning process involves the computation of temporary outputs, comparison of outputs with the desired targets, adjustment of weights and process repetition (if necessary). The research being reported developed a model for training the neural network whose architecture is presented in Figure 7. Modeling was based on the gesture data collected online.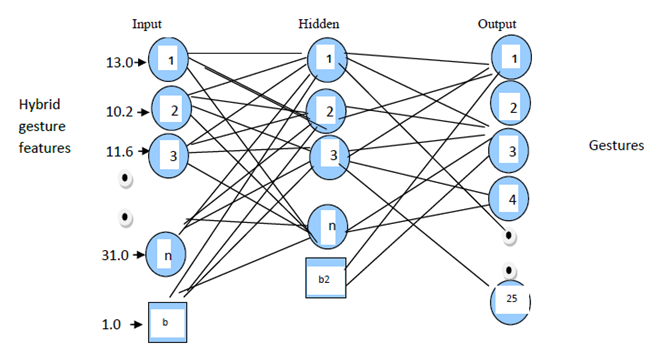 | Figure 7. The Neural Network Model for the Gesture Recognition |
The Back-propagation algorithm is used in training the network. It is a supervised learning algorithm where an error function is defined (based on the training set) and minimized by adjusting the weights using hill climbing algorithm while the Mean Square Error (MSE) serves as the error function to be minimized. The error is calculated as the difference between the target (t) and the actual value (a) of the network output as follows: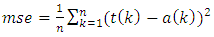 | (12) |
Where n is the number of training set based on multilayer perceptions, back-propagation algorithm was used to adjust the weights and biases of the network in order to minimize the mean square error overall output and examples. The adjustment gives a generalization of the least mean square algorithm whereby an error function is defined to be minimized by using the gradient descent algorithm. The generalized delta rule calculates the error for the current input example and back-propagates it from layer to layer. The training algorithm is presented in (Akintola et al. 2015).At each of the Neuron of the Hidden and the output layers, the weighted sums are calculated, and passed through the activation function f(x). In our case, it is f(wSum – T) where wSum is the weighted sum of the inputs and T is a threshold or bias value. To take care of this biased, it is passed to the network as a node indicated by the rectangular node in the network in Figure 7. The value is 1. The weighted sum (wSum) calculated at each neurode is given below.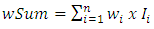 | (13) |
where 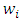 is the value of weight
is the value of weight 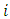 and
and 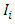 is the input at node
is the input at node 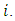 There are various functions that can be used for the activation function, f. such as sigmoid function as depicted in Figure 8. We used the sigmoid function in this work at the hidden layer and linear at the output layer. The sigmoid function and its derivative are defined as:
There are various functions that can be used for the activation function, f. such as sigmoid function as depicted in Figure 8. We used the sigmoid function in this work at the hidden layer and linear at the output layer. The sigmoid function and its derivative are defined as: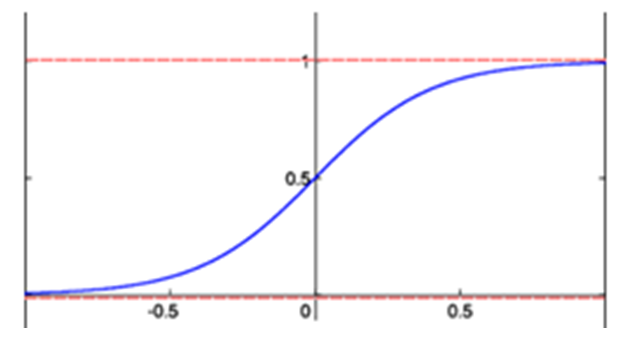 | Figure 8. Sigmoid activation function |
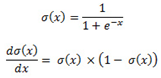 | (14) |
The weights are updated to give the correct output at the output layer. This forms the basis of training the neural network. The weight changes are calculated by using the gradient descent method. This means we follow the steepest path on the error function to try and minimize it. That is we take the error at the output neurons (Desired value – actual value) and multiplying it by the gradient of the sigmoid function. If the difference is positive we need to move up the gradient of the activation function and if its negative we need to move down the gradient of the activation function as depicted in Figure 9.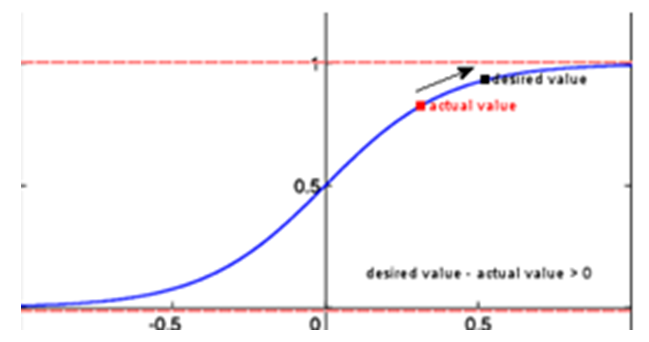 | Figure 9. Error gradient |
The formula to calculate the basic error gradient for each output neuron k is: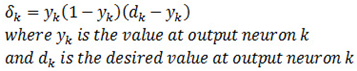 | (15) |
There is a difference between the error gradients at the output and hidden layers. The hidden layer’s error gradient is based on the output layer’s error gradient (back propagation) so for the hidden layer the error gradient for each hidden neuron is the gradient of the activation function multiplied by the weighted sum of the errors at the output layer originating from that neuron. i.e using this formula: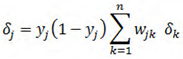 | (16) |
The Weights are updated as follows: | (17) |
The ∝ is the learning rate and it is usually a value between 0 and 1. It affects how large the weight adjustments are and so also affects the learning speed of the network. This value need to be careful selected to provide the best results, too low and it will take ages to learn, too high and the adjustments might be too large and the accuracy will suffer as the network will constantly jump over a better solution and generally get stuck at some sub-optimal accuracy.The operation of modifying the weights are repeated until the training error is minimized efficiently. There are some commonly used stopping conditions used when training a neural network model. They are: desired accuracy or desired mean square error and the elapsed epochs. In this paper 100 elapsed epochs is considered to train the Network. The network parameters for the proposed model consist of an input layer with 19 neurons, one hidden layer with 20 neurons, and one output layer with 25 neurons (MLP 19: 20: 25) as shown in Figure 7. 100 epochs were used with momentum and learning rate set to 0.3. Based on random generators, the initial weights were initialized to small numbers less than 1.
3. Experiment and Result
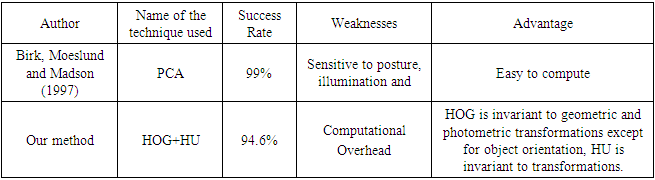
In this research the gray scale image of the hand gesture database from data (2020) extracted in March 2020 is used to test the model. The database consists of 25 hand gesture of International sign languages. A low-cost black and white camera is used to capture the hand gestures which were performed by performer. It produces 8-bit gray level image. The resolution of grabbed image is 256 * 248. Each of the gestures/signs is performed in front of a dark background and the user's arm is covered with a similar black piece of cloth, hence easy segmentation of the hand is easy to carry out using simple background subtraction technique. Each gesture is performed at various scales, translations, and rotation in the plane parallel to the image-plane. 20 images from each of the 25 gesture classes making 500 gestures were used to train the neural network model. Also, another 20 images from each of the 25 gesture classes making another 500 gestures were used to test the model. The results of the recognition were presented using the confusion matrix of the classification as shown in Figure 10. The diagonal values of the confusion matrix of Figure 10 represent the correct classification. It can be seen that the recognition rates of some hand gestures gave 100% while some gave 90% and the least is 75%. On average, a recognition accuracy of 96.4% is achieved. A comparison of our approach with the baseline approach is presented I Table 1. Table 1. Comparison with other methods
 |
| |
|
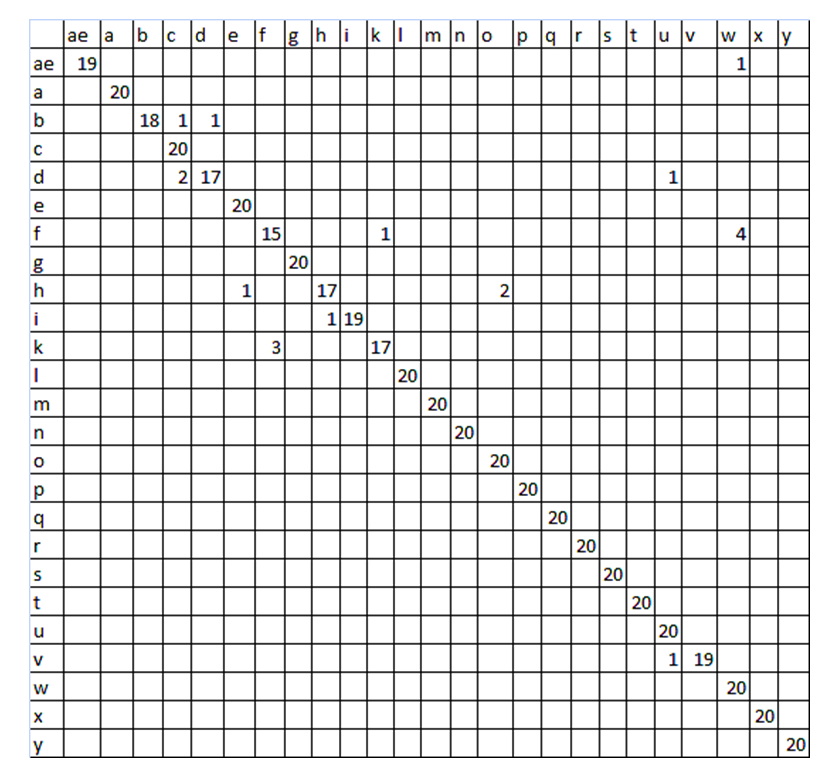 | Figure 10. Confusion Matrix of gesture recognition |
4. Conclusions
In this research, a novel method of static hand gesture recognition technique is carried out. The paper proposed a new hybrid feature using the fusion of the histogram of oriented gradient and the Hu invariant moments. This work heavily relies on efficient background subtraction for it to work well. The two features selected are roughly invariant features which may work well in real time gesture recognition. A test conducted by picking new 20 images from each class of the 25 gestures classes making a total of 500 gestures gives a recognition accuracy of 94.6%. This solves problems of low rate of recognition accuracy in hand gesture recognition. It is shown that the use of histogram of oriented gradient combined with the Hu invariant moments features can effectively characterize the different hand gesture patterns. Experiments prove that the recognition accuracy of the hybrid features using artificial neural network as a classifier performs excellently at static gesture recognition. Future work will look at other classifiers such as Support Vector Machines and other features with the aim of increasing the recognition accuracy.
5. Ethical Approval
This article does not contain any studies with human participants or animals performed by any of the authors.
References
| [1] | Akintola K.G., Akinyokun O.C., Olabode O. Iwasokun G.B. (2015). Object Classification in Videos Using Neural Network: A Case Study of Vehicles and Pedestrians Classification for Surveillance systems, Proceedings of 12th International Conference of the Nigeria Computer Society on Information Technology for Inclusive Development, July 22 - 24, 2015. Pp. 112-120. Akure, Nigeria. |
| [2] | Bamwend J., Özerdem M.S. (2019). Recognition of static hand gesture with using ANN and SVM, Dicle University Journal of Engineering (DUJE). 10:2 (2019) Page 561-568. |
| [3] | Birk H, Moeslund T.B, Madsen C.B (1997) Real-time recognition of hand alphabet gestures using principal component analysis. In: Proceedings of the Scandinavian conference on image analysis, Lappeenranta. |
| [4] | Data (2020) http://www-prima.inrialpes.fr/FGnet/data/12-MoeslundGesture/database.html. |
| [5] | Doulamis A. Doulamis N., Kalisperakis I., Stentoumis C. (2010). A Real- Time Single-Camera Approach for Automatic Fall Detection, International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Vol. xxxviii, Part 5 Commission V Symposium, Newcastle upon Tyne, UK. 2010. |
| [6] | Ghosh D.K. Ari S. (2015). Static Hand Gesture Recognition using Mixture of Features and SVM Classifier, Proceedings of the 5th IEEE Int. Conf. on Communication Systems and Network Technologies (CSNT-2015), At Gwalior. |
| [7] | Heikkila J. and Silven O. (1999). A real-time system for monitoring of cyclists and pedestrians in: Second IEEE Workshop on Visual Surveillance Fort Collins, Colorado (Jun. 1999) pp. 74{81. |
| [8] | Liang R-H Ouhyoung M. (1996) A Sign Language Recognition System Using Hidden Markov Model and Context Sensitive Search. Proc. Of ACM VRST’ 96 (ACM International Symposium on Virtual Reality and Software Technology) pp. 59-66, Hong Kongm 1996. |
| [9] | Nagarajan S. and Subashini T.S. (2013). Static Hand Gesture Recognition for Sign Language Alphabets using Edge Oriented Histogram and Multi Class SVM. International Journal of Computer Applications (0975 – 8887) Volume 82 – No4, November 2013. |
| [10] | Nagashree R. N., Michahial S., Aishwarya G. N., Azeez B.H., Jayalakshmi M. R., Rani R. K. (2015). Hand gesture recognition using support vector machine. The International Journal Of Engineering And Science (IJES) Volume 4 Issue 6. PP.42-46 June - 2015 ISSN (e): 2319 – 1813 ISSN (p): 2319 – 1805. |
| [11] | Rahman M.H. and Afrin J. (2013). Hand Gesture Recognition using Multiclass Support Vector Machine. International Journal of Computer Applications (0975 – 8887) Volume 74– No.1, July 2013. |
| [12] | Yun L., Lifeng Z., Shujun Z. (2012). A Hand Gesture Recognition Method Based on Multi-Feature Fusion and Template Matching. Proceedings of the International Workshop on Information and Electronics Engineering (IWIEE) 2012. pp. 1678-1684. |



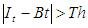

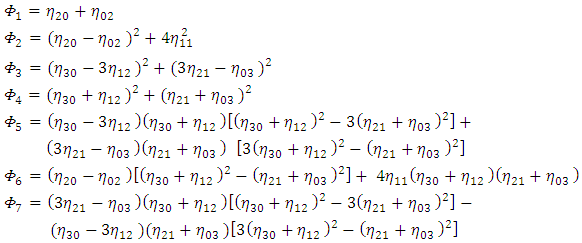
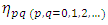 are the normalized central moments defined as:
are the normalized central moments defined as: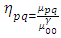
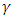 is given as:
is given as: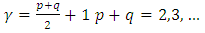
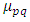 are the central moments calculated as follows:
are the central moments calculated as follows: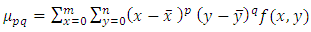
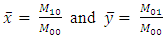
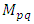 are the
are the 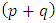 -th order moments:
-th order moments: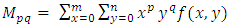

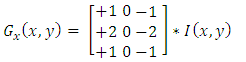
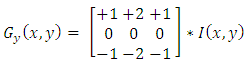
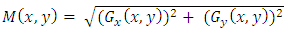
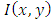 is the image.The gradient direction is computed as follows:
is the image.The gradient direction is computed as follows: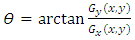



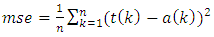
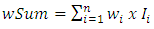
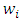 is the value of weight
is the value of weight 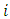 and
and 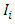 is the input at node
is the input at node 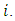 There are various functions that can be used for the activation function, f. such as sigmoid function as depicted in Figure 8. We used the sigmoid function in this work at the hidden layer and linear at the output layer. The sigmoid function and its derivative are defined as:
There are various functions that can be used for the activation function, f. such as sigmoid function as depicted in Figure 8. We used the sigmoid function in this work at the hidden layer and linear at the output layer. The sigmoid function and its derivative are defined as:
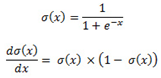

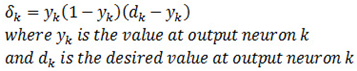
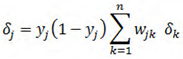


 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
