Chiang-Cheng Chiang, Pen-Chun Lu
Department of Electrical Engineering, Tatung University, Taipei, Taiwan, Republic of China
Correspondence to: Chiang-Cheng Chiang, Department of Electrical Engineering, Tatung University, Taipei, Taiwan, Republic of China.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This paper considers the problem of observer-based hierarchical sliding mode control approach for uncertain underactuated systems with time delay and input saturation in strict-feedback form. Based on sliding mode control technique and the concept of hierarchical design, an adaptive fuzzy hierarchical sliding mode controller is designed for the uncertain nonlinear system by using fuzzy logic systems to approximate the uncertain functions. Additionally, input saturation which is one of the most important input constraints usually appear in many industrial control systems. By choosing an appropriate Lyapunov–Krasovskii function, the proposed controller is designed to demonstrate that all the signals in the closed-loop system can not only guarantee uniformly ultimately bounded, but also achieve good tracking performance. Finally, some computer simulation results of a practical example are illustrated to verify the effectiveness of the proposed approach.
Keywords:
Underactuated system, Lyapunov–Krasovskii function, Strict-feedback form, Hierarchical sliding mode control, Time delay, Input saturation, Fuzzy logic systems
Cite this paper: Chiang-Cheng Chiang, Pen-Chun Lu, Observer-Based Hierarchical Sliding Mode Control of Uncertain Underactuated Systems with Time Delay and Input Saturation, American Journal of Intelligent Systems, Vol. 9 No. 1, 2019, pp. 29-38. doi: 10.5923/j.ajis.20190901.02.
1. Introduction
During the past decades, underactuated systems have drawn much attention and some significant results have been obtained in the literature. Wu et al. [1] cope with the problem of fault detection for underactuated manipulators. Lai et al. [2] deal with the problem of the stable control strategy for the planar three-link underactuated mechanical system. Recently, for systems with special structure, i.e. strict-feedback form, many research results have been proposed in [3-5]. In this paper, the underactuated systems in strict-feedback form are investigated and some systematic methodologies are proposed to solve the tracking control problem.In practice, input saturation is one of the most important input constraints which are usually utilized in many industrial control systems. In addition, because saturation is a potential factor degrading the control system performance, it often gives rise to undesirable inaccuracy, or even affects system stability. In recent years, Chen et al. [6] introduced an adaptive neural-network backstepping control approach for a class of uncertain nonlinear systems in the presence of input saturation. Liu et al. [7] investigated the problem of the observer-based neural control method for MIMO pure-feedback non-linear systems with input saturation and disturbances.A general sliding-mode control (SMC) is established in this paper for a class of uncertain underactuated systems. As a kind of highly robust variable structural control method, the sliding-mode controller is able to respond quickly, insensitivity to systemic parameters, good transient performance, external disturbance, and so on. Due to the underactuated characteristic of the controlled system, at least two sliding surfaces with specific relation are employed for the controller design. For the aggregated hierarchical structure of a sliding-mode controller, the underactuated system is segmented into several subsystems. For each part, we design a first-layer sliding surface. Then, the first-layer sliding surfaces are utilized to construct the second-layer sliding surface. By theoretical analysis, the conclusion is made that all sliding surfaces of the SMC structure is asymptotically stable.Fuzzy logic systems are introduced to approximate unknown non-linear functions. An adaptive fuzzy control technique for the problem of time delay is verified by Lyapunov-Krasovskii function. Long et al. [8] investigated the problem of adaptive fuzzy output-feedback control for switched uncertain non-linear systems. In [9], Li et al. introduced an adaptive fuzzy output-feedback stabilization controller to treat the problem for a class of switched nonstrict-feedback nonlinear systems.The main contribution of this paper is that the proposed hierarchical sliding mode control method deals with the problem of tracking performance and stability for a class of underactuated systems in strict-feedback form with input saturation and time delay. Based on sliding mode control technique and the concept of hierarchical design, an adaptive fuzzy hierarchical sliding mode controller is designed for the underactuated system by using fuzzy logic systems to approximate uncertain functions. The fuzzy state observer is employed to estimate the unavailable state for measurement. Choosing an appropriate Lyapunov-Krasovskii function, it is theoretically ensured that all the signals in the closed-loop system are uniformly ultimately bounded and obtain good tracking performance under our designed controller.The remainder of the paper is organized as follows. Section II describes the problem formulation and preliminaries together with the definition of fuzzy logic systems (FLSs) are given. In Section III, adaptive fuzzy hierarchical sliding mode controller and observer are designed for a class of uncertain underactuated nonlinear time-delay systems with saturation input and the stability analysis of the whole system is also verified by Lyapunov-Krasovskii functional. Some computer simulation results of a practical example are demonstrated to show the effectiveness of the proposed approach in Section IV. Finally, the conclusion is drawn in Section V.
2. Problem Statement and Preliminaries
2.1. Problem Statement
Consider a class of single-input-multi-output uncertain underactuated nonlinear systems in strict-feedback form with input saturation expressed as follows: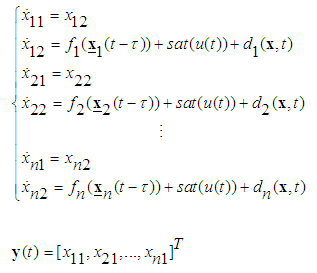 | (1) |
Eq. (1) can be rewritten as | (2) |
where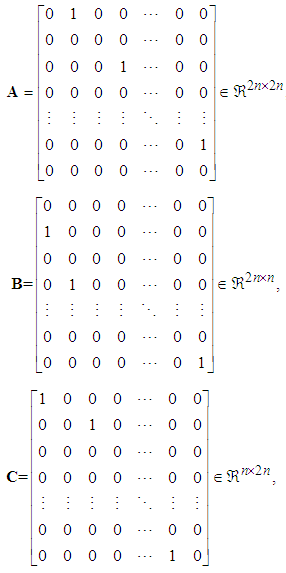
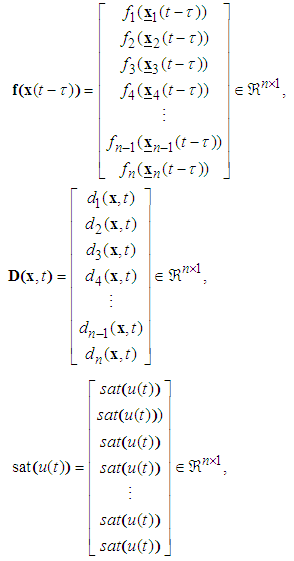 where
where 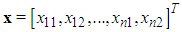 is the system state vector which is assumed to be unavailable for measurement,
is the system state vector which is assumed to be unavailable for measurement, 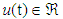 and
and 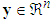 are input and output of the system, respectively.
are input and output of the system, respectively. 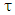 is the value of time delay.
is the value of time delay. 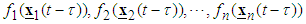 are unknown real continuous nonlinear functions where
are unknown real continuous nonlinear functions where 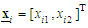 , for
, for 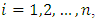 and
and 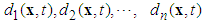 are unknown external bound disturbances.
are unknown external bound disturbances. 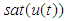 denotes the nonlinear saturation characteristic. Without loss of generality, the following assumptions are made for the controller design:Assumption 1: The time delay
denotes the nonlinear saturation characteristic. Without loss of generality, the following assumptions are made for the controller design:Assumption 1: The time delay 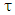 is a fixed and known constant.Assumption 2:
is a fixed and known constant.Assumption 2: 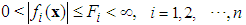 for all x, where
for all x, where 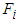 are known positive constants. In order to deal with the control constraints for convenience, the saturation function
are known positive constants. In order to deal with the control constraints for convenience, the saturation function 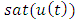 can be rewritten as
can be rewritten as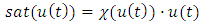 | (3) |
where 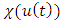 be expressed as
be expressed as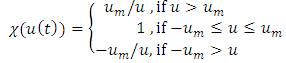 | (4) |
Assumption 3: 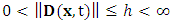 ,where h is an unknown constant.Control Objective: Design a controller for (1) such that the system output
,where h is an unknown constant.Control Objective: Design a controller for (1) such that the system output 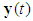 would track the desired output vector
would track the desired output vector 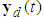 , where
, where 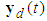 is the bounded desired signal and contains the finite derivative up to the second order. Define the vector of the output tracking error as
is the bounded desired signal and contains the finite derivative up to the second order. Define the vector of the output tracking error as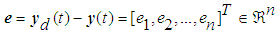 | (5) |
2.2. Description of Fuzzy Logic Systems
The fuzzy logic system performs a mapping from 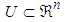 to
to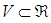 . Let
. Let 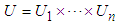 where
where 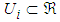 ,
, 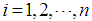 . The fuzzy rule base consists of a collection of fuzzy IF-THEN rules:
. The fuzzy rule base consists of a collection of fuzzy IF-THEN rules: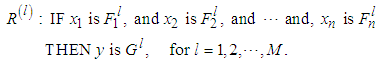 | (6) |
in which 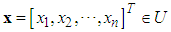 and
and 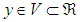 are the input and output of the fuzzy logic system,
are the input and output of the fuzzy logic system, 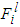 and
and 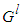 are fuzzy sets in
are fuzzy sets in 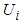 and
and 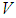 , respectively. The fuzzifier maps a crisp point
, respectively. The fuzzifier maps a crisp point 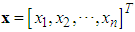 into a fuzzy set in
into a fuzzy set in 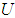 . The fuzzy inference engine performs a mapping from fuzzy sets in
. The fuzzy inference engine performs a mapping from fuzzy sets in 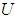 to fuzzy sets in
to fuzzy sets in 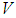 , based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in
, based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in 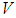 to a crisp point in
to a crisp point in 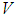 . The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form:
. The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form: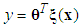 | (7) |
where 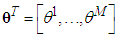 with each variable
with each variable 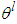 as the point at which the fuzzy membership function of
as the point at which the fuzzy membership function of 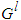 achieves the maximum value and
achieves the maximum value and 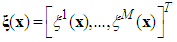 with each variable
with each variable 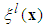 as the fuzzy basis function defined as
as the fuzzy basis function defined as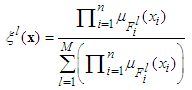 | (8) |
where 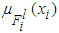 is the membership function of the fuzzy set.
is the membership function of the fuzzy set.
3. Controller Design and Stability Analysis
First, let the unknown nonlinear functions 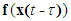 can be approximated, over a compact set
can be approximated, over a compact set 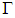 , by the fuzzy logic systems as follows:
, by the fuzzy logic systems as follows: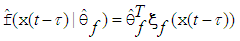 | (9) |
where 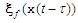 is the fuzzy basis vector,
is the fuzzy basis vector, 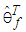 is the corresponding adjustable parameter vectors of each fuzzy logic systems.Owing to the unavailable states of the system in many practical systems, the fuzzy logic system (9) is not used to control nonlinear systems whose states are not obtained for measurement. Therefore, an observer is employed to estimate the unavailable states. Now, let
is the corresponding adjustable parameter vectors of each fuzzy logic systems.Owing to the unavailable states of the system in many practical systems, the fuzzy logic system (9) is not used to control nonlinear systems whose states are not obtained for measurement. Therefore, an observer is employed to estimate the unavailable states. Now, let 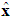 be defined as the estimates of
be defined as the estimates of 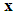 . Then, we can obtain the following fuzzy logic systems as
. Then, we can obtain the following fuzzy logic systems as 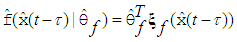 | (10) |
In order to estimate the state, we design the observer for system (2) as follows: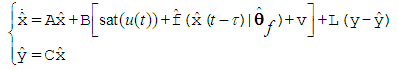 | (11) |
where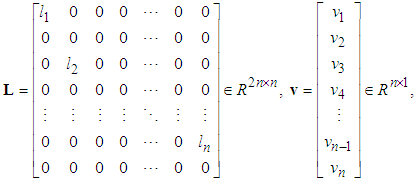 L is the observer gain matrix to guarantee the characteristic polynomial of
L is the observer gain matrix to guarantee the characteristic polynomial of 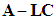 to be Hurwitz. Let us define the estimation error vector as
to be Hurwitz. Let us define the estimation error vector as 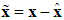 and
and 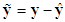 , then by (2) and (10), we obtain
, then by (2) and (10), we obtain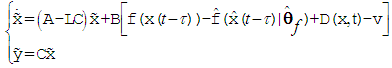 | (12) |
It is assumed that 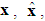 and
and 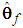 belong to compact sets
belong to compact sets 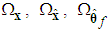 , respectively, which are defined as
, respectively, which are defined as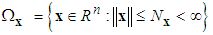 | (13) |
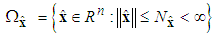 | (14) |
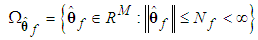 | (15) |
where 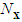 ,
, 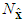 , and
, and 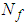 are the designed parameters, and
are the designed parameters, and 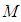 is the number of fuzzy inference rules. Let us define the optimal parameter vector
is the number of fuzzy inference rules. Let us define the optimal parameter vector 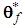 as follows:
as follows: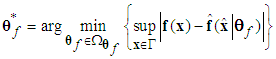 | (16) |
where 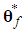 is bounded in the suitable closed set
is bounded in the suitable closed set 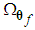 .The parameter estimation errors can be defined as
.The parameter estimation errors can be defined as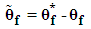 | (17) |
and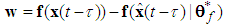 | (18) |
is the minimum approximation errors, which correspond to approximation errors obtained when optimal parameters are used.Applying (17) and (18) into (12), we obtain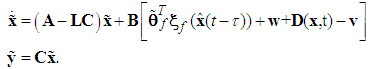 | (19) |
The output error dynamics of (19) can be expressed as follows: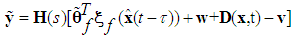 | (20) |
where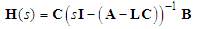 | (21) |
and s denotes the complex Laplace transform variable. As has been discussed, we could not obtain all elements of 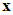 , because not all states of the system are available for measurement. Hence, we could not obtain all elements of
, because not all states of the system are available for measurement. Hence, we could not obtain all elements of 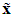 . We will employ the state variable filters [11] to cope with this problem. First, we choose a stable filter
. We will employ the state variable filters [11] to cope with this problem. First, we choose a stable filter 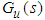 as the following form:
as the following form: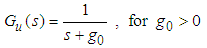 | (22) |
And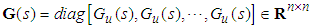 | (23) |
Introducing (23) into (20), we can obtain the steady-state equation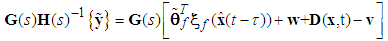 | (24) |
Define a set of state variable filters 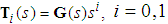 , thus,
, thus,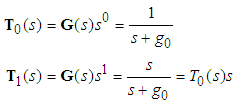 | (25) |
The corresponding filtered signals are defined as follows: 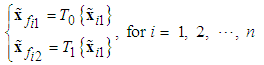 | (26) |
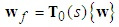 | (27) |
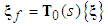 | (28) |
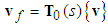 | (29) |
and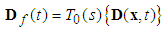 | (30) |
Then, Eq. (19) can be rewritten as follows: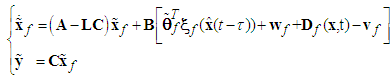 | (31) |
where 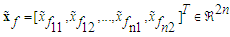 We define
We define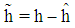 | (32) |
and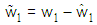 | (33) |
where 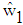 and
and 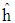 are the estimated of
are the estimated of 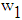 and
and 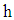 , respectively.where
, respectively.where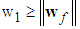 | (34) |
Based on Lyapunov stable theorem, we can obtain the robust compensation term 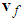 and the parameter update laws as follows:
and the parameter update laws as follows: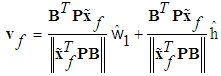 | (35) |
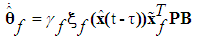 | (36) |
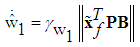 | (37) |
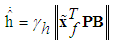 | (38) |
where 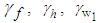 are positive constants.Remark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we have to use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [10]. The proposed adaptive law (35)-(38) can be modified as the following form:
are positive constants.Remark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we have to use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [10]. The proposed adaptive law (35)-(38) can be modified as the following form: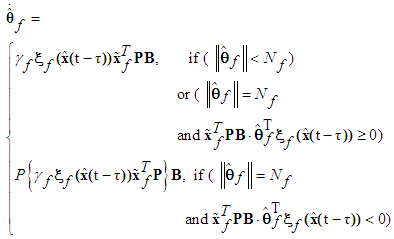 | (39) |
where 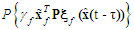 is defined as
is defined as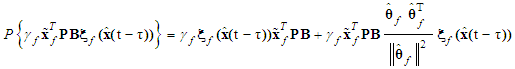 | (40) |
The main result of robust adaptive fuzzy observer scheme is summarized on the following theorem.Theorem 1: Consider the single-input-multi-output uncertain underactuated system (1). The robust adaptive fuzzy observer is defined by (10) with adaptation laws given by (35)-(38). For the given positive definite matrix 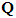 , if there exist symmetric positive definite matrix
, if there exist symmetric positive definite matrix 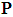 such that the following Lyapunov equation
such that the following Lyapunov equation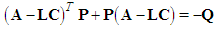 | (41) |
is satisfied, then all the closed-loop signals are bound, and the estimation errors converge to a neighborhood of zero.Proof. Consider the Lyapunov function candidate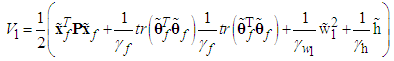 | (42) |
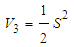 | (43) |
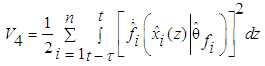 | (44) |
By the time derivative of 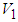 and the facts
and the facts 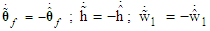 we obtain
we obtain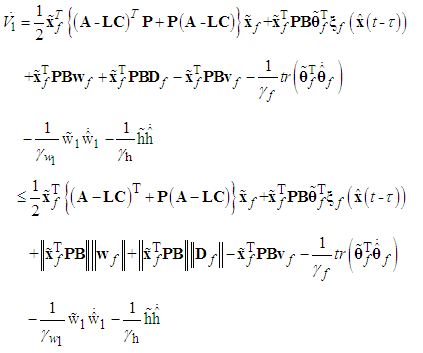 | (45) |
Applying Assumption 3 and (34) yields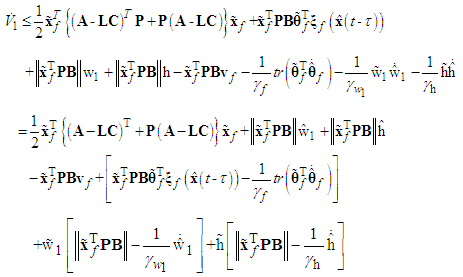 | (46) |
By employing (35)-(38), we can get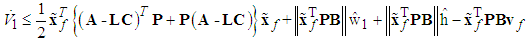 | (47) |
Then using the robust compensation term 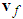 as shown in (35), the above equation can be rewritten as
as shown in (35), the above equation can be rewritten as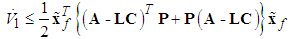 | (48) |
According to (41), it can be easily shown that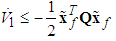 | (49) |
Therefore, it can be concluded that 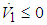 from (49), and the estimation errors of the closed-loop system converges asymptotically to a neighborhood of zero based on Lyapunov synthesis approach. This completes the proof.Next, we design the observer-based incremental sliding mode controller. Define the sliding surfaces as follows:
from (49), and the estimation errors of the closed-loop system converges asymptotically to a neighborhood of zero based on Lyapunov synthesis approach. This completes the proof.Next, we design the observer-based incremental sliding mode controller. Define the sliding surfaces as follows: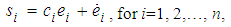 | (50) |
where 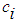 are positive constants.Differentiating
are positive constants.Differentiating 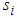 with respect to time and from (5), we have
with respect to time and from (5), we have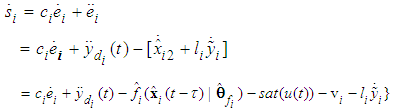 | (51) |
Then, the second-level sliding surface can be defined as follows: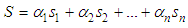 | (52) |
where 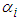 , for i=1,2,…,n, are sliding mode parameters which maybe remain constant or change according to different conditions.Based on the fuzzy logic systems and the states of the system are not obtained for measurement, the equivalent control law can be obtained as
, for i=1,2,…,n, are sliding mode parameters which maybe remain constant or change according to different conditions.Based on the fuzzy logic systems and the states of the system are not obtained for measurement, the equivalent control law can be obtained as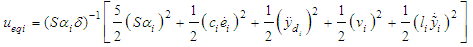 | (53) |
and 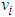 can be obtained by backward from
can be obtained by backward from 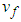 .Then we define:
.Then we define: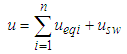 | (54) |
where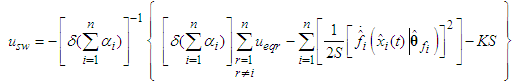 | (55) |
for a positive constant 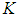 .Theorem 2: Consider the single-input-multi-output underactuated system (1). If Assumptions 1-3 are satisfied, then the proposed adaptive fuzzy sliding mode controller defined by (54) with adaptive laws (35)-(38) guarantees that all signals of the closed-loop system are bounded, and the output tracking errors converge to a neighborhood of zero. If the choice of
.Theorem 2: Consider the single-input-multi-output underactuated system (1). If Assumptions 1-3 are satisfied, then the proposed adaptive fuzzy sliding mode controller defined by (54) with adaptive laws (35)-(38) guarantees that all signals of the closed-loop system are bounded, and the output tracking errors converge to a neighborhood of zero. If the choice of 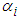 , which ensures that
, which ensures that 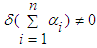 , satisfies
, satisfies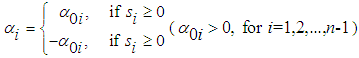 | (56) |
and 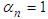 such that
such that 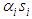 , for i=1,2,…,n-1 and
, for i=1,2,…,n-1 and 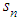 are the same sign. Then, the first-level sliding surfaces
are the same sign. Then, the first-level sliding surfaces 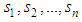 are also asymptotically stable.Proof:Consider the Lyapunov function candidate
are also asymptotically stable.Proof:Consider the Lyapunov function candidate 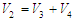 Differentiating the
Differentiating the 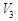 and
and 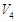 with respect to time, we can obtain
with respect to time, we can obtain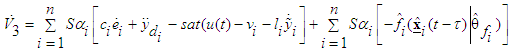 | (57) |
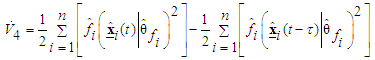 | (58) |
With the use of 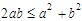 for scalars a and b, we obtain
for scalars a and b, we obtain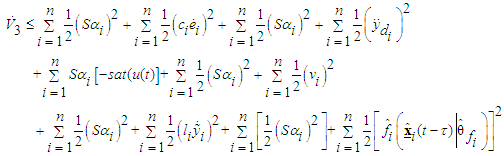 | (59) |
According to (58), (59) and 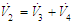 , we have
, we have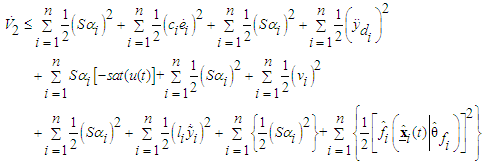 | (60) |
By introducing (3) into (60), we obtain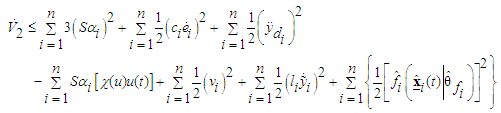 | (61) |
since 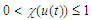 according to the density property of a real number [12], there exists a constant
according to the density property of a real number [12], there exists a constant 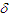 that satisfies
that satisfies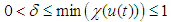 | (62) |
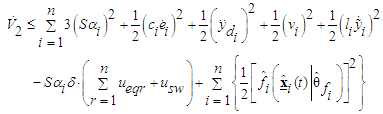 | (63) |
Then substituting the equivalent control 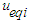 in (53) into (63), we have
in (53) into (63), we have 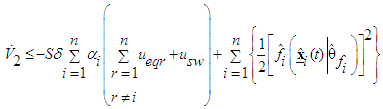 | (64) |
Using the switching control law (53), one can obtain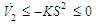 | (65) |
Therefore, it can be concluded that 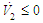 from (65), and all the signals of the closed-loop system converge asymptotically to a neighborhood of zero based on the Lyapunov synthesis approach. This completes the proof.
from (65), and all the signals of the closed-loop system converge asymptotically to a neighborhood of zero based on the Lyapunov synthesis approach. This completes the proof.
4. An Example and Simulation Results
In this section, a mass-spring-damper system [8] in the presence of uncertain parameter and exogenous disturbances is considered as our simulation example as shown in Fig. 1, and described by the following form: | (66) |
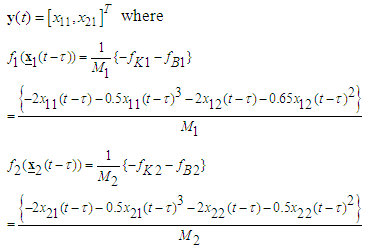 and
and 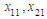 are the displacement of the mass,
are the displacement of the mass, 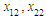 are the velocity of the mass,
are the velocity of the mass, 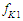 and
and 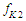 are the spring force,
are the spring force, 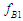 and
and 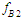 are the friction force.
are the friction force.  are the body mass, and
are the body mass, and 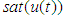 is the force of saturation. The disturbances are assumed to be
is the force of saturation. The disturbances are assumed to be 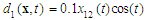 and
and 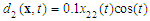 .
.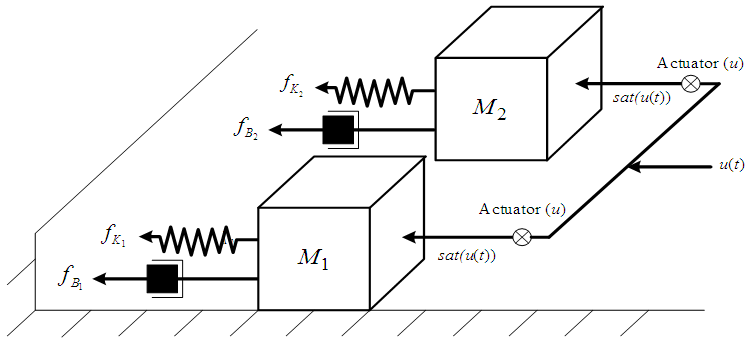 | Figure 1. The mass-spring-damper system |
In the implementation, six fuzzy sets are defined over interval [-3, 3] for  , with labels NB, NM, NS, PS, PM, and PB, and their membership functions are
, with labels NB, NM, NS, PS, PM, and PB, and their membership functions are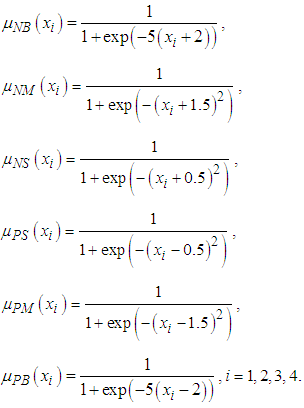 In this case, the control objective is to maintain the system output
In this case, the control objective is to maintain the system output 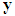 to follow the reference signal
to follow the reference signal 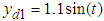 and
and 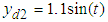 . First, we select the observer gain matrix as
. First, we select the observer gain matrix as  . The sliding surfaces are selected as
. The sliding surfaces are selected as 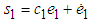 and
and 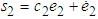 , where
, where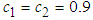 , the second-level sliding surface is constructed as
, the second-level sliding surface is constructed as 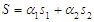 , where
, where 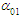 = 1.1 and
= 1.1 and 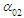 = 2. The initial values are chosen as
= 2. The initial values are chosen as 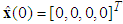 ,
,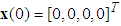 ,
, 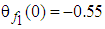 ,
, 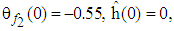 and
and 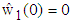 . The other parameters are selected as
. The other parameters are selected as 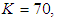
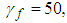
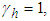
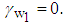 The simulation results are shown in Figs. 2-10. Fig. 2 and Fig. 3 show the trajectories of the system states and desired outputs. Figs. 4-5 show the trajectories of the system states and their estimation states. The performances of sliding dynamics are shown in Figs. 6-8. Figs. 9-10 demonstrate the trajectories of the system functions. From the simulation results, the tracking error and the estimation error converge asymptotically to a neighborhood of zero, respectively. The simulation results verify the usefulness of the proposed robust adaptive fuzzy sliding mode controller. Moreover, the unknown system functions can be approximated well based on the proposed adaptive laws.Remark 2: In this paper, the time delay, the state estimator, and input saturation are considered simultaneously, which are different from the previous literature [6] and [8].
The simulation results are shown in Figs. 2-10. Fig. 2 and Fig. 3 show the trajectories of the system states and desired outputs. Figs. 4-5 show the trajectories of the system states and their estimation states. The performances of sliding dynamics are shown in Figs. 6-8. Figs. 9-10 demonstrate the trajectories of the system functions. From the simulation results, the tracking error and the estimation error converge asymptotically to a neighborhood of zero, respectively. The simulation results verify the usefulness of the proposed robust adaptive fuzzy sliding mode controller. Moreover, the unknown system functions can be approximated well based on the proposed adaptive laws.Remark 2: In this paper, the time delay, the state estimator, and input saturation are considered simultaneously, which are different from the previous literature [6] and [8].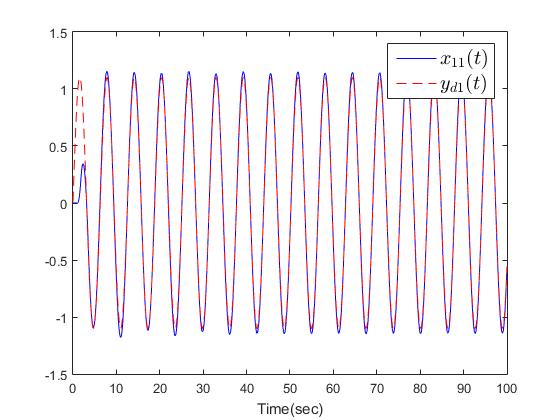 | Figure 2. The outputs  |
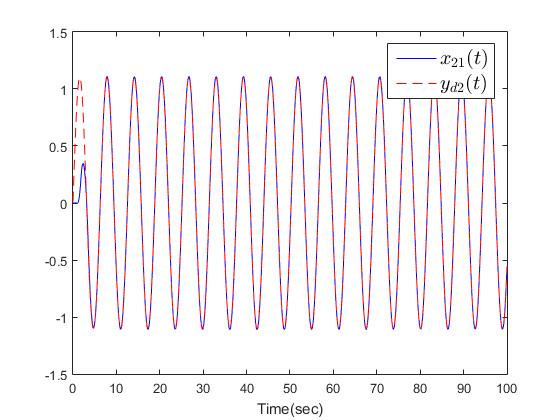 | Figure 3. The outputs  |
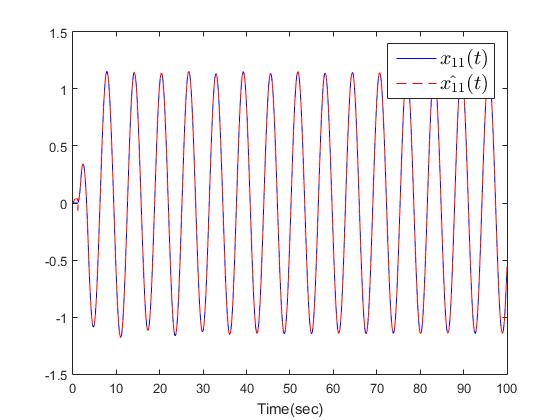 | Figure 4. The trajectories of  |
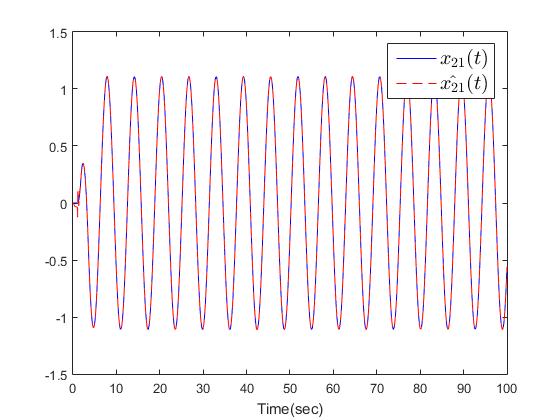 | Figure 5. The trajectories of 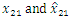 |
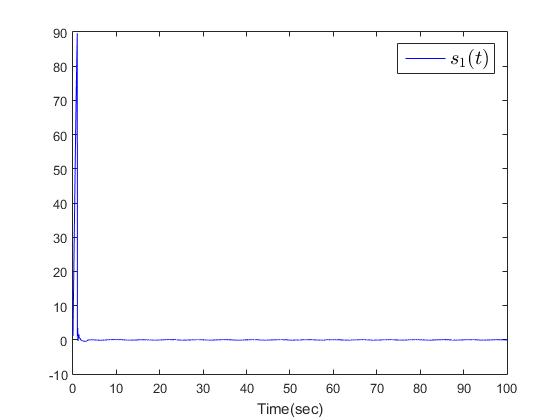 | Figure 6. The first-level sliding surface 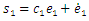 |
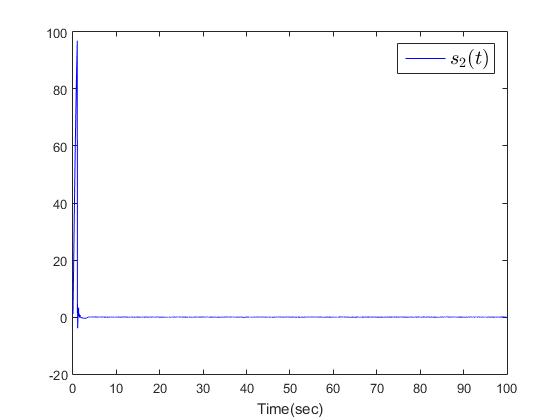 | Figure 7. The first-level sliding surface 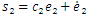 |
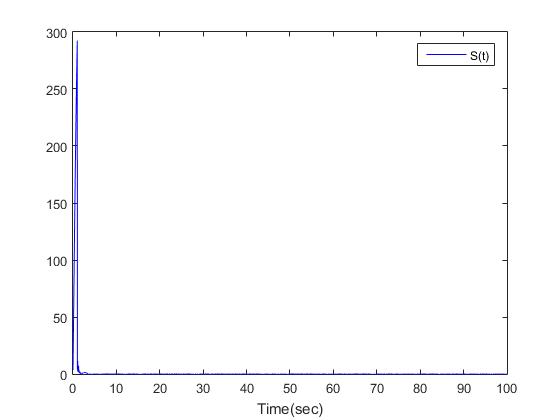 | Figure 8. The second-level sliding surface 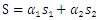 |
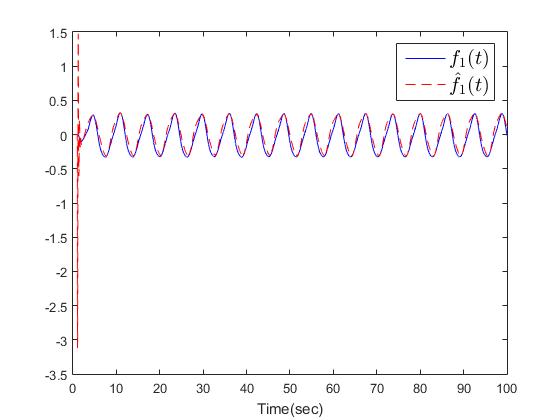 | Figure 9. The trajectories of  |
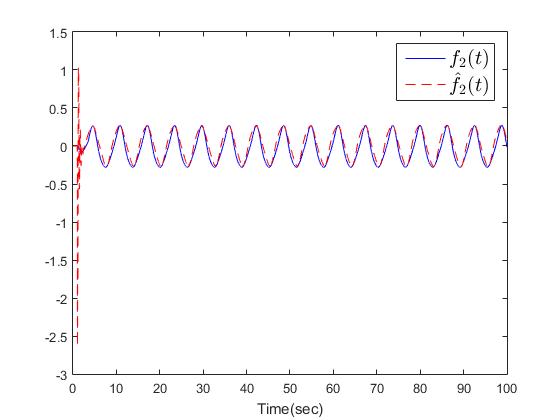 | Figure 10. The trajectories of  |
5. Conclusions
The main contribution of this paper is to develop the hierarchical sliding mode control method to tackle the problem of tracking performance and stability analysis for a class of uncertain underactuated systems in strict-feedback form with input saturation and time delay. Based on sliding mode control technique and the concept of hierarchical design, the unknown system functions can be approximated by the fuzzy logic systems with some adaptive laws. Also, the fuzzy state observer is employed to estimate the unavailable state for measurement. Moreover, choosing an appropriate Lyapunov-Krasovskii function, it is theoretically ensured that all the signals in the closed-loop system are uniformly ultimately bounded and the tracking performance can be achieved under our proposed control approach.
References
| [1] | L. Wu, W. Luo, Y. Zeng, F. Li, and Z. Zheng, “Fault detection for underactuated manipulators modeled by markovian jump systems,” IEEE Transactions on Industrial Electronics, vol. 63, no. 7, pp. 4387-4399, Jul. 2016. |
| [2] | X. Lai, Y. Wang, M. Wu, and W. Cao, “Stable control strategy for planar three-link underactuated mechanical system,” IEEE/ASME Transactions on Mechatronics, vol. 21, no. 3, pp. 1345-1356, Jun. 2016. |
| [3] | Z. H. Zhang and G. H. Yang, “Time-varying threshold-based fault detection for a class of uncertain non-linear systems in strict-feedback form,” IET Control Theory & Applications, vol. 10, no. 17, pp. 2149-2159, Nov. 2016. |
| [4] | H. Zargarzadeh, T. Dierks, and S. Jagannathan, “Optimal control of nonlinear continuous-time systems in strict-feedback form,” IEEE Transactions on Neural Networks and Learning Systems, vol. 26, no. 10, pp. 2535-2549, Oct. 2015. |
| [5] | B. Xu, Z. Shi, C. Yang, and F. Sun, “Composite neural dynamic surface control of a class of uncertain nonlinear systems in strict-feedback form,” IEEE Transactions on Cybernetics, vol. 44, no. 12, pp. 2626-2634, Dec. 2014. |
| [6] | M. Chen, G. Tao, and B. Jiang, “Dynamic surface control using neural networks for a class of uncertain nonlinear systems with input saturation,” IEEE Transactions on Neural Networks and Learning Systems, vol. 26, no. 9, pp. 2086-2097, Sep. 2015. |
| [7] | W. Liu, J. Lu, Z. Zhang, and S. Xu, “Observer-based neural control for MIMO pure-feedback non-linear systems with input saturation and disturbances,” IET Control Theory & Applications, vol. 10, no. 17, pp. 2314-2324, Nov. 2016. |
| [8] | L. Long and J. Zhao, “Adaptive fuzzy output-feedback control for switched uncertain non-linear systems,” IET Control Theory & Applications, vol. 10, no. 7, pp. 752-761, Apr. 2016. |
| [9] | Y. Li and S. Tong, “Adaptive fuzzy output-feedback stabilization control for a class of switched nonstrict-feedback nonlinear systems,” IEEE Transactions on Cybernetics, vol. 47, no. 4, pp. 1007-1016, Apr. 2017. |
| [10] | L. X. Wang, A course in fuzzy systems and control, Englewood Cliffs, NJ: Prentice-Hall, 1997. |
| [11] | C. C. Kung and T. H. Chen, “Observer-based indirect adaptive fuzzy integral sliding mode control with state variable filters,” Fuzzy Sets and Syst., vol. 155, no. 2, pp. 292–308, 2005. |
| [12] | Z. Zhu, Y. Xia, and M. Fu, "Adaptive sliding mode control for attitude stabilization with actuator saturation," IEEE Transactions on Industrial Electronics, vol. 58, no. 10, pp. 4898-4907, Oct. 2011. |
| [13] | J. H. Park and G. T. Park, “Adaptive fuzzy observer with minimal dynamic order for uncertain nonlinear systems,” IEE Proc. Theory & Applications, vol. 150, no. 2, pp. 189-197, 2003. |
| [14] | W. Wang, X. d. Liu, and J. q. Yi, “Structure design of two types of sliding-mode controllers for a class of under-actuated mechanical systems,” IET Control Theory & Applications, vol. 1, no. 1, pp. 163-172, Jan. 2007. |


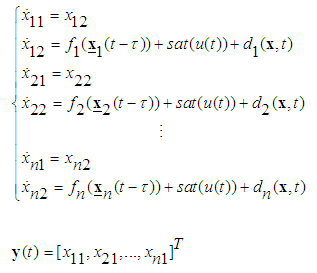


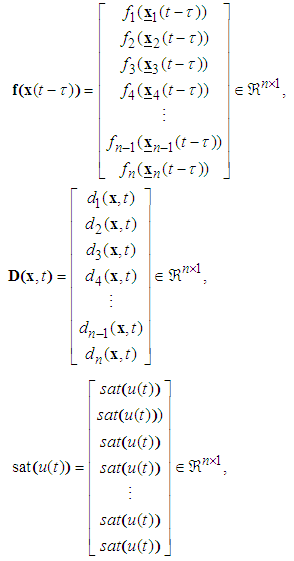 where
where 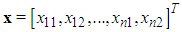 is the system state vector which is assumed to be unavailable for measurement,
is the system state vector which is assumed to be unavailable for measurement, 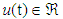 and
and 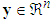 are input and output of the system, respectively.
are input and output of the system, respectively. 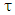 is the value of time delay.
is the value of time delay. 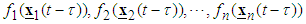 are unknown real continuous nonlinear functions where
are unknown real continuous nonlinear functions where 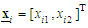 , for
, for 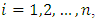 and
and 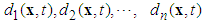 are unknown external bound disturbances.
are unknown external bound disturbances. 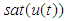 denotes the nonlinear saturation characteristic. Without loss of generality, the following assumptions are made for the controller design:Assumption 1: The time delay
denotes the nonlinear saturation characteristic. Without loss of generality, the following assumptions are made for the controller design:Assumption 1: The time delay 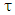 is a fixed and known constant.Assumption 2:
is a fixed and known constant.Assumption 2: 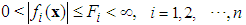 for all x, where
for all x, where 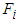 are known positive constants. In order to deal with the control constraints for convenience, the saturation function
are known positive constants. In order to deal with the control constraints for convenience, the saturation function 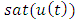 can be rewritten as
can be rewritten as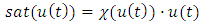
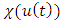 be expressed as
be expressed as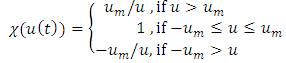
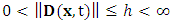 ,where h is an unknown constant.Control Objective: Design a controller for (1) such that the system output
,where h is an unknown constant.Control Objective: Design a controller for (1) such that the system output 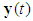 would track the desired output vector
would track the desired output vector 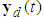 , where
, where 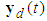 is the bounded desired signal and contains the finite derivative up to the second order. Define the vector of the output tracking error as
is the bounded desired signal and contains the finite derivative up to the second order. Define the vector of the output tracking error as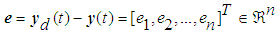
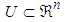 to
to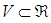 . Let
. Let 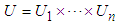 where
where 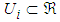 ,
, 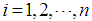 . The fuzzy rule base consists of a collection of fuzzy IF-THEN rules:
. The fuzzy rule base consists of a collection of fuzzy IF-THEN rules: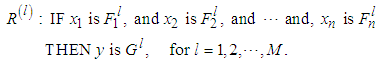
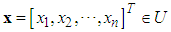 and
and 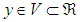 are the input and output of the fuzzy logic system,
are the input and output of the fuzzy logic system, 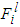 and
and 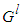 are fuzzy sets in
are fuzzy sets in 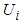 and
and 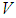 , respectively. The fuzzifier maps a crisp point
, respectively. The fuzzifier maps a crisp point 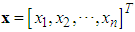 into a fuzzy set in
into a fuzzy set in 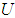 . The fuzzy inference engine performs a mapping from fuzzy sets in
. The fuzzy inference engine performs a mapping from fuzzy sets in 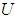 to fuzzy sets in
to fuzzy sets in 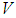 , based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in
, based upon the fuzzy IF-THEN rules in the fuzzy rule base and the compositional rule of inference. The defuzzifier maps a fuzzy set in 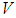 to a crisp point in
to a crisp point in 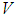 . The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form:
. The fuzzy systems with center-average defuzzifier, product inference and singleton fuzzifier are of the following form: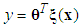
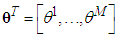 with each variable
with each variable 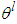 as the point at which the fuzzy membership function of
as the point at which the fuzzy membership function of 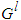 achieves the maximum value and
achieves the maximum value and 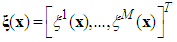 with each variable
with each variable 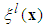 as the fuzzy basis function defined as
as the fuzzy basis function defined as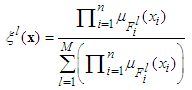
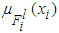 is the membership function of the fuzzy set.
is the membership function of the fuzzy set.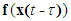 can be approximated, over a compact set
can be approximated, over a compact set  , by the fuzzy logic systems as follows:
, by the fuzzy logic systems as follows: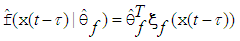
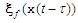 is the fuzzy basis vector,
is the fuzzy basis vector, 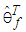 is the corresponding adjustable parameter vectors of each fuzzy logic systems.Owing to the unavailable states of the system in many practical systems, the fuzzy logic system (9) is not used to control nonlinear systems whose states are not obtained for measurement. Therefore, an observer is employed to estimate the unavailable states. Now, let
is the corresponding adjustable parameter vectors of each fuzzy logic systems.Owing to the unavailable states of the system in many practical systems, the fuzzy logic system (9) is not used to control nonlinear systems whose states are not obtained for measurement. Therefore, an observer is employed to estimate the unavailable states. Now, let 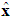 be defined as the estimates of
be defined as the estimates of 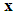 . Then, we can obtain the following fuzzy logic systems as
. Then, we can obtain the following fuzzy logic systems as 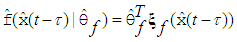
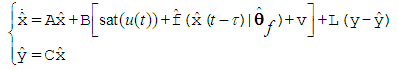
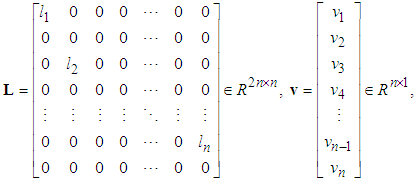 L is the observer gain matrix to guarantee the characteristic polynomial of
L is the observer gain matrix to guarantee the characteristic polynomial of 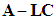 to be Hurwitz. Let us define the estimation error vector as
to be Hurwitz. Let us define the estimation error vector as 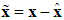 and
and 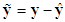 , then by (2) and (10), we obtain
, then by (2) and (10), we obtain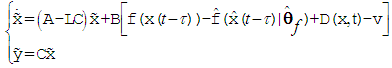
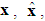 and
and 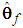 belong to compact sets
belong to compact sets 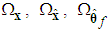 , respectively, which are defined as
, respectively, which are defined as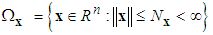
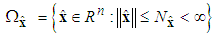
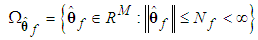
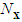 ,
, 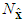 , and
, and 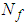 are the designed parameters, and
are the designed parameters, and 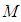 is the number of fuzzy inference rules. Let us define the optimal parameter vector
is the number of fuzzy inference rules. Let us define the optimal parameter vector 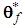 as follows:
as follows: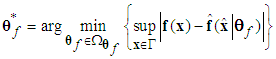
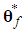 is bounded in the suitable closed set
is bounded in the suitable closed set 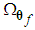 .The parameter estimation errors can be defined as
.The parameter estimation errors can be defined as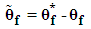
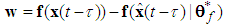
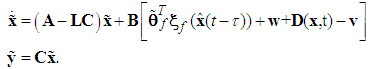
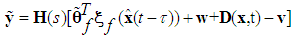
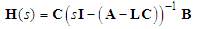
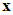 , because not all states of the system are available for measurement. Hence, we could not obtain all elements of
, because not all states of the system are available for measurement. Hence, we could not obtain all elements of 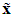 . We will employ the state variable filters [11] to cope with this problem. First, we choose a stable filter
. We will employ the state variable filters [11] to cope with this problem. First, we choose a stable filter 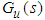 as the following form:
as the following form: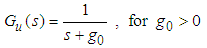
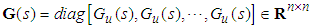
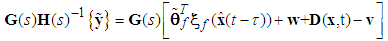
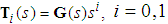 , thus,
, thus,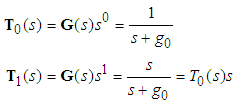
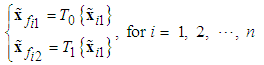
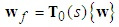
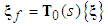
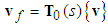
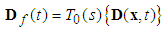
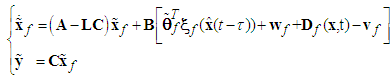
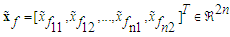 We define
We define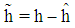
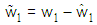
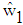 and
and 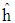 are the estimated of
are the estimated of 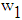 and
and 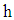 , respectively.where
, respectively.where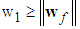
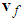 and the parameter update laws as follows:
and the parameter update laws as follows: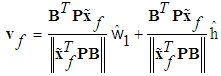
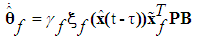
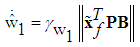
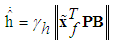
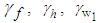 are positive constants.Remark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we have to use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [10]. The proposed adaptive law (35)-(38) can be modified as the following form:
are positive constants.Remark 1: Without loss of generality, the adaptive laws used in this paper are assumed that the parameter vectors are within the constraint sets or on the boundaries of the constraint sets but moving toward the inside of the constraint sets. If the parameter vectors are on the boundaries of the constraint sets but moving toward the outside of the constraint sets, we have to use the projection algorithm to modify the adaptive laws such that the parameter vectors will remain inside of the constraint sets. Readers can refer to reference [10]. The proposed adaptive law (35)-(38) can be modified as the following form: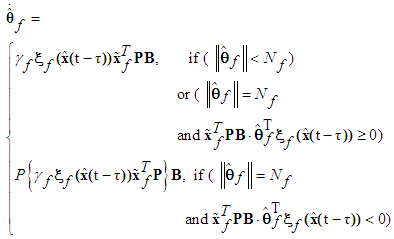
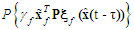 is defined as
is defined as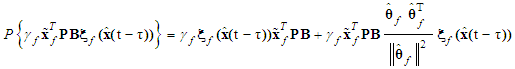
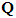 , if there exist symmetric positive definite matrix
, if there exist symmetric positive definite matrix 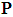 such that the following Lyapunov equation
such that the following Lyapunov equation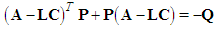
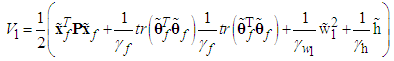
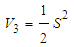
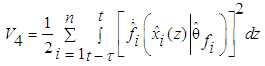
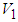 and the facts
and the facts 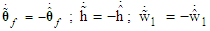 we obtain
we obtain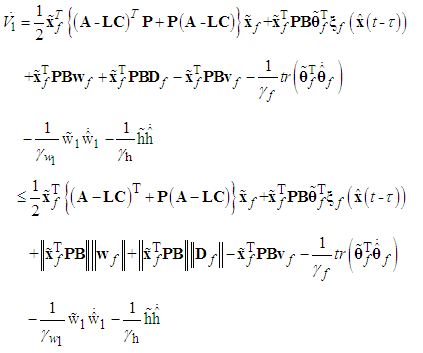
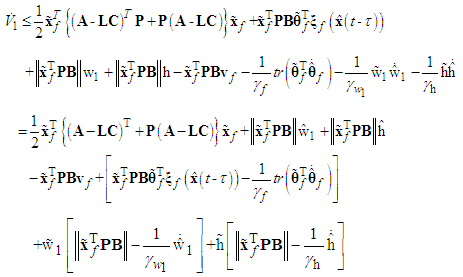
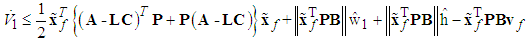
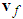 as shown in (35), the above equation can be rewritten as
as shown in (35), the above equation can be rewritten as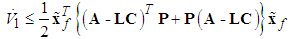
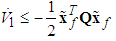
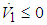 from (49), and the estimation errors of the closed-loop system converges asymptotically to a neighborhood of zero based on Lyapunov synthesis approach. This completes the proof.Next, we design the observer-based incremental sliding mode controller. Define the sliding surfaces as follows:
from (49), and the estimation errors of the closed-loop system converges asymptotically to a neighborhood of zero based on Lyapunov synthesis approach. This completes the proof.Next, we design the observer-based incremental sliding mode controller. Define the sliding surfaces as follows: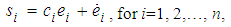
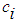 are positive constants.Differentiating
are positive constants.Differentiating 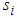 with respect to time and from (5), we have
with respect to time and from (5), we have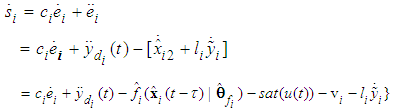
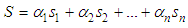
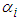 , for i=1,2,…,n, are sliding mode parameters which maybe remain constant or change according to different conditions.Based on the fuzzy logic systems and the states of the system are not obtained for measurement, the equivalent control law can be obtained as
, for i=1,2,…,n, are sliding mode parameters which maybe remain constant or change according to different conditions.Based on the fuzzy logic systems and the states of the system are not obtained for measurement, the equivalent control law can be obtained as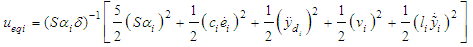
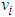 can be obtained by backward from
can be obtained by backward from 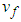 .Then we define:
.Then we define: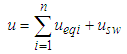
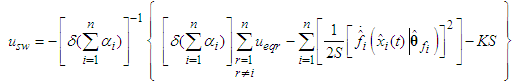
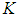 .Theorem 2: Consider the single-input-multi-output underactuated system (1). If Assumptions 1-3 are satisfied, then the proposed adaptive fuzzy sliding mode controller defined by (54) with adaptive laws (35)-(38) guarantees that all signals of the closed-loop system are bounded, and the output tracking errors converge to a neighborhood of zero. If the choice of
.Theorem 2: Consider the single-input-multi-output underactuated system (1). If Assumptions 1-3 are satisfied, then the proposed adaptive fuzzy sliding mode controller defined by (54) with adaptive laws (35)-(38) guarantees that all signals of the closed-loop system are bounded, and the output tracking errors converge to a neighborhood of zero. If the choice of 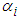 , which ensures that
, which ensures that 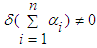 , satisfies
, satisfies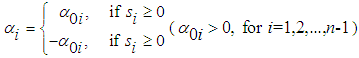
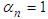 such that
such that 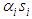 , for i=1,2,…,n-1 and
, for i=1,2,…,n-1 and 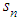 are the same sign. Then, the first-level sliding surfaces
are the same sign. Then, the first-level sliding surfaces 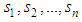 are also asymptotically stable.Proof:Consider the Lyapunov function candidate
are also asymptotically stable.Proof:Consider the Lyapunov function candidate 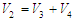 Differentiating the
Differentiating the 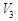 and
and 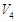 with respect to time, we can obtain
with respect to time, we can obtain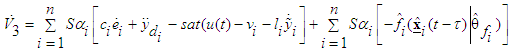
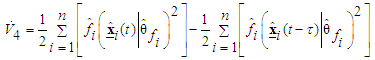
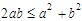 for scalars a and b, we obtain
for scalars a and b, we obtain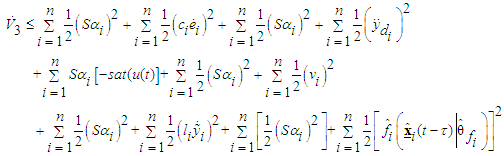
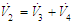 , we have
, we have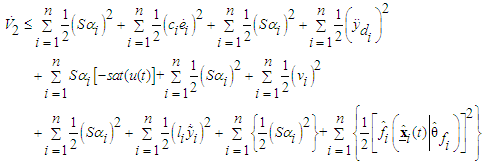
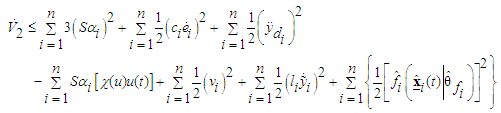
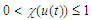 according to the density property of a real number [12], there exists a constant
according to the density property of a real number [12], there exists a constant 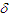 that satisfies
that satisfies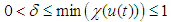
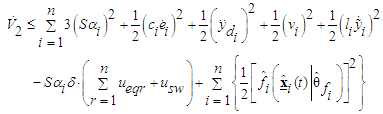
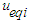 in (53) into (63), we have
in (53) into (63), we have 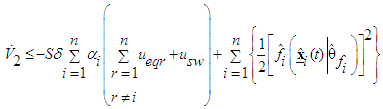
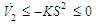
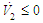 from (65), and all the signals of the closed-loop system converge asymptotically to a neighborhood of zero based on the Lyapunov synthesis approach. This completes the proof.
from (65), and all the signals of the closed-loop system converge asymptotically to a neighborhood of zero based on the Lyapunov synthesis approach. This completes the proof.
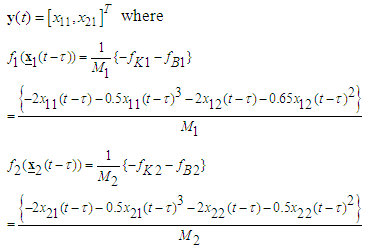 and
and 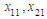 are the displacement of the mass,
are the displacement of the mass, 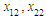 are the velocity of the mass,
are the velocity of the mass, 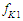 and
and 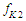 are the spring force,
are the spring force, 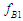 and
and 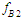 are the friction force.
are the friction force.  are the body mass, and
are the body mass, and 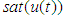 is the force of saturation. The disturbances are assumed to be
is the force of saturation. The disturbances are assumed to be 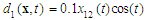 and
and 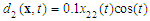 .
.
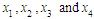 , with labels NB, NM, NS, PS, PM, and PB, and their membership functions are
, with labels NB, NM, NS, PS, PM, and PB, and their membership functions are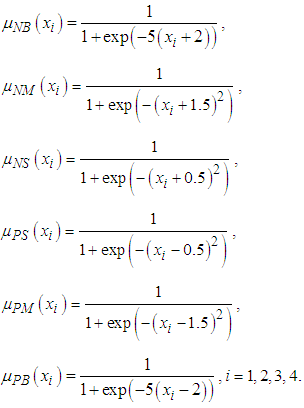 In this case, the control objective is to maintain the system output
In this case, the control objective is to maintain the system output 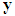 to follow the reference signal
to follow the reference signal 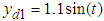 and
and 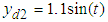 . First, we select the observer gain matrix as
. First, we select the observer gain matrix as  . The sliding surfaces are selected as
. The sliding surfaces are selected as 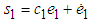 and
and 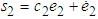 , where
, where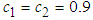 , the second-level sliding surface is constructed as
, the second-level sliding surface is constructed as 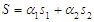 , where
, where 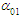 = 1.1 and
= 1.1 and 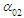 = 2. The initial values are chosen as
= 2. The initial values are chosen as 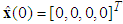 ,
,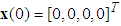 ,
, 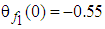 ,
, 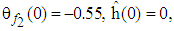 and
and 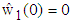 . The other parameters are selected as
. The other parameters are selected as 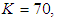
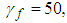
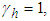
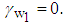 The simulation results are shown in Figs. 2-10. Fig. 2 and Fig. 3 show the trajectories of the system states and desired outputs. Figs. 4-5 show the trajectories of the system states and their estimation states. The performances of sliding dynamics are shown in Figs. 6-8. Figs. 9-10 demonstrate the trajectories of the system functions. From the simulation results, the tracking error and the estimation error converge asymptotically to a neighborhood of zero, respectively. The simulation results verify the usefulness of the proposed robust adaptive fuzzy sliding mode controller. Moreover, the unknown system functions can be approximated well based on the proposed adaptive laws.Remark 2: In this paper, the time delay, the state estimator, and input saturation are considered simultaneously, which are different from the previous literature [6] and [8].
The simulation results are shown in Figs. 2-10. Fig. 2 and Fig. 3 show the trajectories of the system states and desired outputs. Figs. 4-5 show the trajectories of the system states and their estimation states. The performances of sliding dynamics are shown in Figs. 6-8. Figs. 9-10 demonstrate the trajectories of the system functions. From the simulation results, the tracking error and the estimation error converge asymptotically to a neighborhood of zero, respectively. The simulation results verify the usefulness of the proposed robust adaptive fuzzy sliding mode controller. Moreover, the unknown system functions can be approximated well based on the proposed adaptive laws.Remark 2: In this paper, the time delay, the state estimator, and input saturation are considered simultaneously, which are different from the previous literature [6] and [8].
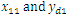

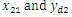

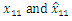

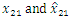

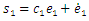

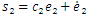

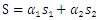


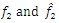
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML