-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Intelligent Systems
p-ISSN: 2165-8978 e-ISSN: 2165-8994
2018; 8(1): 6-11
doi:10.5923/j.ajis.20180801.02

Large Data Analysis via Interpolation of Functions: Interpolating Polynomials vs Artificial Neural Networks
Rohit Raturi
Enterprise Solutions, KPMG LLP, Montvale, USA
Correspondence to: Rohit Raturi, Enterprise Solutions, KPMG LLP, Montvale, USA.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this article we study function interpolation problem from interpolating polynomials and artificial neural networks point of view. Function interpolation plays a very important role in many areas of experimental and theoretical sciences. Usual means of function interpolation are interpolation polynomials (Lagrange, Newton, splines, Bezier, etc.). Here we show that a specific strategy of function interpolation realized by means of artificial neural networks is much efficient than, e.g., Lagrange interpolation polynomial.
Keywords: Function interpolation, Approximation, Artificial intelligence, Input layer, Output layer, Hidden layer, Optimization, Weight, Bias, Machine learning
Cite this paper: Rohit Raturi, Large Data Analysis via Interpolation of Functions: Interpolating Polynomials vs Artificial Neural Networks, American Journal of Intelligent Systems, Vol. 8 No. 1, 2018, pp. 6-11. doi: 10.5923/j.ajis.20180801.02.
Article Outline
1. Introduction
- Interpolation of functions is one of the most desirable methods of mathematical analysis. The main problem of function interpolation can be formulated as follows. It is given a finite set of couples1
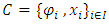 where I is a finite set of indexes. The problem is to construct a function,
where I is a finite set of indexes. The problem is to construct a function,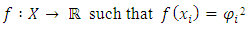 Here
Here 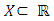 is the given interval of the variable
is the given interval of the variable 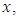 on which the interpolation is required. Naturally,
on which the interpolation is required. Naturally, 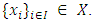 Depending on the specific problem under consideration,
Depending on the specific problem under consideration, 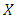 can be bounded or unbounded.Applications of the function interpolation ranges from numerical solution of ordinary and partial differential equations to solution of the best fitting problem for finite sets of data. Usually, real-life observations or measurements at discrete time-instants are gathered in a data set like
can be bounded or unbounded.Applications of the function interpolation ranges from numerical solution of ordinary and partial differential equations to solution of the best fitting problem for finite sets of data. Usually, real-life observations or measurements at discrete time-instants are gathered in a data set like 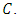 For example, in astronomical observations of a planetary motion,
For example, in astronomical observations of a planetary motion, 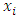 are the time-instants when the coordinate
are the time-instants when the coordinate 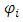 of the center of mass of a planet is measured. In bio-laboratory,
of the center of mass of a planet is measured. In bio-laboratory, 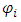 maybe the state of a mouse at time-instant
maybe the state of a mouse at time-instant 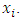 The radiation intensity
The radiation intensity 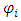 is measured at discrete points
is measured at discrete points 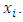 Finally, in particle tracing experiments,
Finally, in particle tracing experiments, 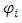 may be the coordinate of a particle observed at the time-instant
may be the coordinate of a particle observed at the time-instant 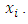 In all those examples, it is a very important and challenging problem to know the measuring quantity at all (even non-measured) time-instants. This problem is usually solved by the methods of function interpolation theory [1-3].
In all those examples, it is a very important and challenging problem to know the measuring quantity at all (even non-measured) time-instants. This problem is usually solved by the methods of function interpolation theory [1-3].2. Methods of Interpolation
- The theory of function interpolation suggests a variety of methods to tackle such problems. The main tool of function interpolation is the construction of appropriate interpolating polynomials. There exists a handful of interpolating polynomials used in real-life applications. The most known interpolation types are piecewise constant interpolation, linear interpolation, polynomial interpolation, spline interpolation, rational interpolation, Padé approximant, Whittaker-Shannon interpolation (when
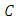 is infinite), Hermite interpolation (when both the values of a function and its derivatives are given), wavelets, Gaussian processes (when the interpolating data contain some noise), etc. The choice of a specific interpolating method depends on such criteria as interpolation accuracy, low cost computer realization, ability to cover sparse data sets, etc.The most delicate analysis require large and sparse data sets. For instance, in the case of large data sets, in order to perform a delicate analysis, the interval
is infinite), Hermite interpolation (when both the values of a function and its derivatives are given), wavelets, Gaussian processes (when the interpolating data contain some noise), etc. The choice of a specific interpolating method depends on such criteria as interpolation accuracy, low cost computer realization, ability to cover sparse data sets, etc.The most delicate analysis require large and sparse data sets. For instance, in the case of large data sets, in order to perform a delicate analysis, the interval 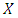 must be split into a large number of sub-intervals where the data (observations, measurements, etc.) are easier to interpolate. Then, interpolating functions are interpolated in each sub-interval and eventually the unknown function is represented as the totality of sub-interpolants. In other words, let
must be split into a large number of sub-intervals where the data (observations, measurements, etc.) are easier to interpolate. Then, interpolating functions are interpolated in each sub-interval and eventually the unknown function is represented as the totality of sub-interpolants. In other words, let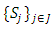 be a splitting of the set
be a splitting of the set 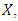 i.e,
i.e,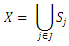 and let
and let 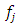 be the corresponding interpolants, i.e.,
be the corresponding interpolants, i.e.,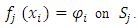 Then, the unknown function on the whole
Then, the unknown function on the whole 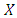 is defined as follows:
is defined as follows: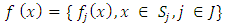 Here
Here 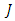 is a finite set of indexes. The choice of
is a finite set of indexes. The choice of 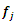 is conditioned by the choice of the splitting
is conditioned by the choice of the splitting 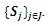 If
If 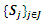 contains only several points, then the simple interpolation tools such as piecewise constant or linear interpolation can be used efficiently. Schematic representation of the above mentioned is brought in Fig 1.
contains only several points, then the simple interpolation tools such as piecewise constant or linear interpolation can be used efficiently. Schematic representation of the above mentioned is brought in Fig 1.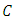 consists of only two couples. In such cases, the interpolating function is given as follows:
consists of only two couples. In such cases, the interpolating function is given as follows: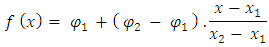 Sometimes, piecewise constant (linear) interpolation is combined with the splitting method above to construct a linear interpolating function within each interval of splitting:
Sometimes, piecewise constant (linear) interpolation is combined with the splitting method above to construct a linear interpolating function within each interval of splitting: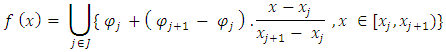 In the case of regularly distributed points, polynomial interpolation is usually used. The most common polynomial interpolating functions are:1. Lagrange interpolating polynomial:
In the case of regularly distributed points, polynomial interpolation is usually used. The most common polynomial interpolating functions are:1. Lagrange interpolating polynomial: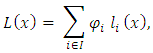 Where
Where 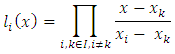 2. Newton interpolating polynomial:
2. Newton interpolating polynomial: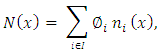 Where
Where 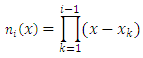
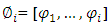 is the ith divided difference;3. Chebyshev interpolating polynomials of the first and second kinds:
is the ith divided difference;3. Chebyshev interpolating polynomials of the first and second kinds: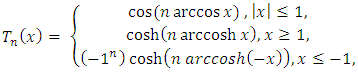
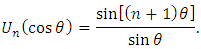 In the case of very dense data sets, the spline interpolation is more proffered than polynomial interpolation. As it is well-known, splines are defined piecewise in terms of polynomials of required order:
In the case of very dense data sets, the spline interpolation is more proffered than polynomial interpolation. As it is well-known, splines are defined piecewise in terms of polynomials of required order: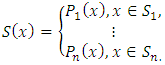 Thus, instead of piecewise constant (linear) interpolating functions, splines provide polynomial interpolation within each sub-interval of the splitting. In the case of periodic or almost periodic data, such as tidal or climate change observation, trigonometric polynomials are used:
Thus, instead of piecewise constant (linear) interpolating functions, splines provide polynomial interpolation within each sub-interval of the splitting. In the case of periodic or almost periodic data, such as tidal or climate change observation, trigonometric polynomials are used: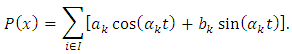
3. Artificial Neural Networks and Function Interpolation
- Artificial neural networks possessing the ability of trained analysis and prediction may be especially advantageous in function interpolation. There exists several algorithms for constructing interpolation of a function by means of artificial neural networks. See, for instance, [5-18] and the related references therein for relevant studies.The interest towards function interpolation by means of artificial neural networks increased during recent years is conditioned by the advantage shown in the numerical procedure of constructing the interpolating function. Due to the ability of prediction, neural networks allow to consider much less nodes than any other method of interpolation. Thus, solving the same problem requiring a much less computational time and resources. The numerical analysis carried out in the next section shows that it provides a better approximation of two special functions compared with the Lagrange interpolating polynomials with 50 and 100 nodes, respectively.
4. Comparison of Lagrange Interpolating Polynomial and Artificial Neural Network Interpolation
- In this section we carry out a numerical comparison between interpolation of some well-known specific functions by means of the Lagrange interpolating polynomial and artificial neural networks.First, let us consider the rectangular function defined according to the piecewise rule
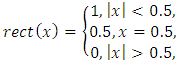 Rectangular function has many applications in electrical engineering and signal processing. Besides, it serves as an activation function for many advanced neural networks.The rect function also can be expressed in terms of the Heaviside
Rectangular function has many applications in electrical engineering and signal processing. Besides, it serves as an activation function for many advanced neural networks.The rect function also can be expressed in terms of the Heaviside 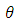 function as follows:
function as follows: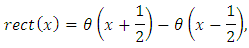 Or
Or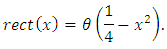 Let us remind that the Heaviside function is defined as follows:
Let us remind that the Heaviside function is defined as follows: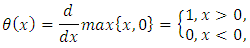 Figures 2-4 show the numerical comparison of the interpolation of the rect function by means of Lagrange interpolating polynomial and artificial neural networks. Figure 3 shows that when we consider 50 nodes within
Figures 2-4 show the numerical comparison of the interpolation of the rect function by means of Lagrange interpolating polynomial and artificial neural networks. Figure 3 shows that when we consider 50 nodes within  , the quadratic error between the Lagrange interpolating polynomial and artificial neural network interpolation dramatically decreases up to 6th epochs. From 7th epoch on, the quadratic error remains almost unaltered and is of
, the quadratic error between the Lagrange interpolating polynomial and artificial neural network interpolation dramatically decreases up to 6th epochs. From 7th epoch on, the quadratic error remains almost unaltered and is of  order.
order.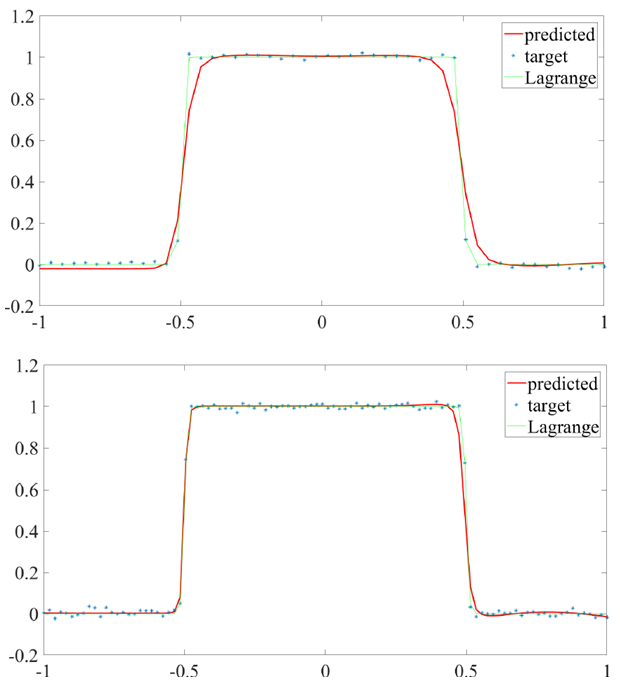 | Figure 2. Approximation of rect function in 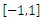 50 nodes (upper) and 100 nodes (lower): ANN algorithm requires 10 and 15 iterations, respectively 50 nodes (upper) and 100 nodes (lower): ANN algorithm requires 10 and 15 iterations, respectively |
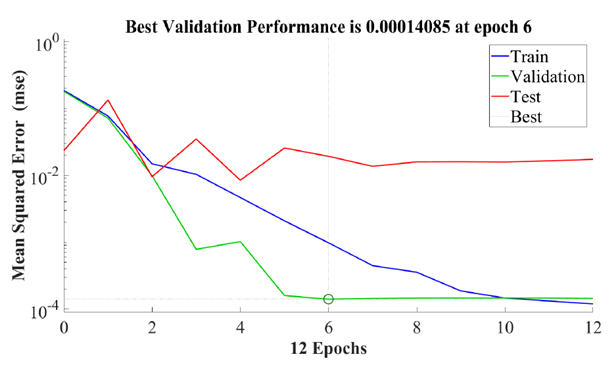 | Figure 3. Quadratic error approximation of rect function in 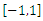 with 100 nodes with 100 nodes |
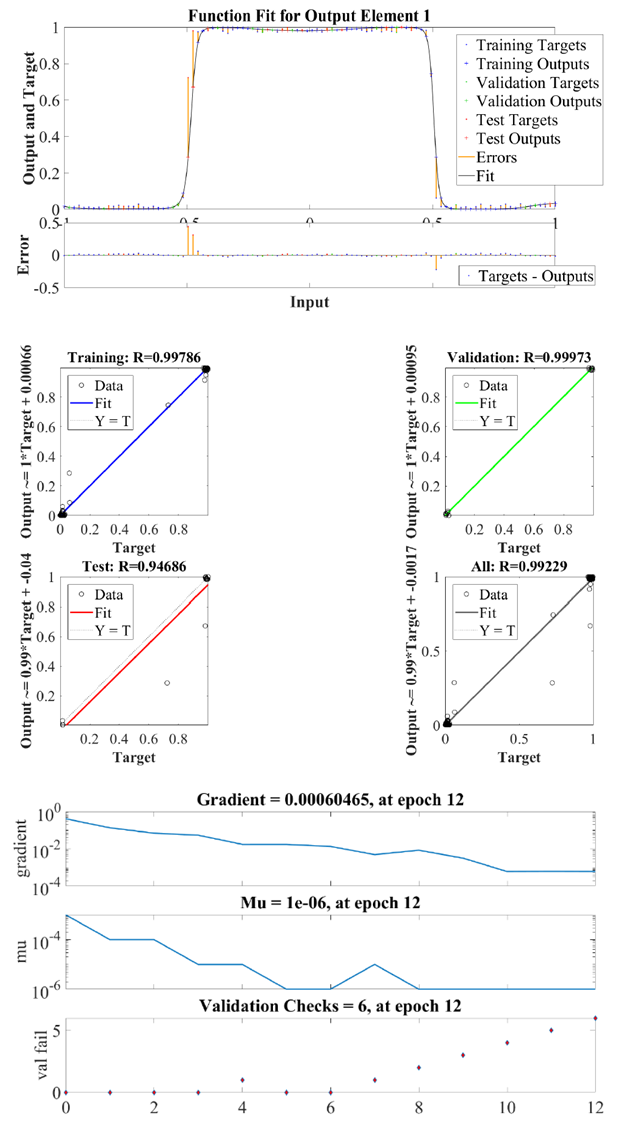 | Figure 4. Function fit (upper) and regression behaviour (middle) and network performance (lower) for rect function in 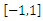 with 100 nodes with 100 nodes |
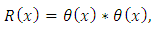 where * denotes the convolution operation. Ramp function and has many applications in engineering (it is used in the so-called half-wave rectification, which is used to convert alternating current into direct current by allowing only positive voltages), artificial neural networks (it serves as an activation function), finance, statistics, fluid mechanics, etc.According to the definition of the Heaviside function, the rump function can be represented also as
where * denotes the convolution operation. Ramp function and has many applications in engineering (it is used in the so-called half-wave rectification, which is used to convert alternating current into direct current by allowing only positive voltages), artificial neural networks (it serves as an activation function), finance, statistics, fluid mechanics, etc.According to the definition of the Heaviside function, the rump function can be represented also as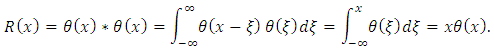 The numerical comparison of the interpolation of the ramp function by means of Lagrange interpolating polynomial and artificial neural networks is shown in Figures 5-7. Figure 6 shows that when we consider 50 nodes within
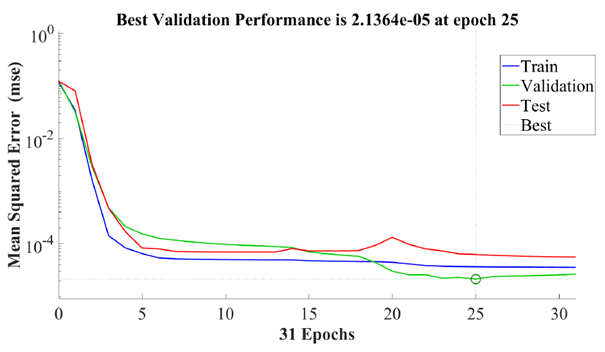
The numerical comparison of the interpolation of the ramp function by means of Lagrange interpolating polynomial and artificial neural networks is shown in Figures 5-7. Figure 6 shows that when we consider 50 nodes within 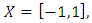 the quadratic error between the Lagrange interpolating polynomial and artificial neural network interpolation dramatically decreases up to 5th epochs. From 6th epoch on, the quadratic error remains almost unaltered and is of
the quadratic error between the Lagrange interpolating polynomial and artificial neural network interpolation dramatically decreases up to 5th epochs. From 6th epoch on, the quadratic error remains almost unaltered and is of 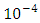 order.
order.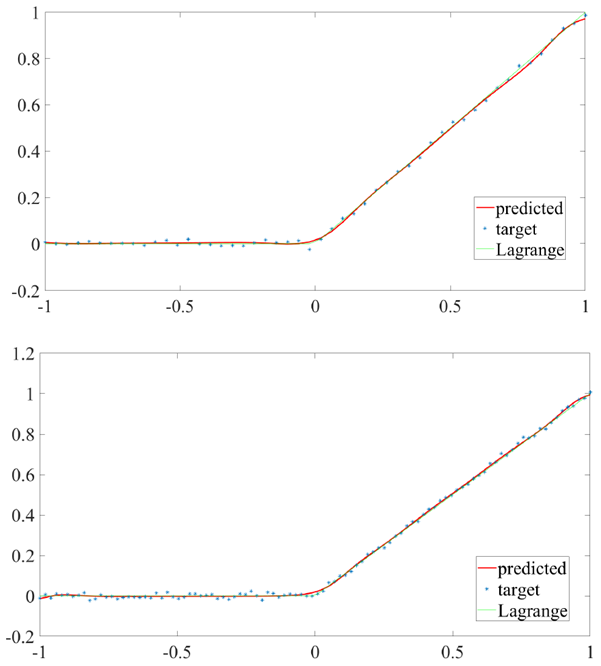 | Figure 5. Approximation of R function in 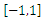 with 50 nodes (upper) and 100 nodes (lower): ANN algorithm requires 15 and 29 iterations, respectively with 50 nodes (upper) and 100 nodes (lower): ANN algorithm requires 15 and 29 iterations, respectively |
 | Figure 6. Quadratic error approximation of R function in 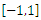 with 100 nodes with 100 nodes |
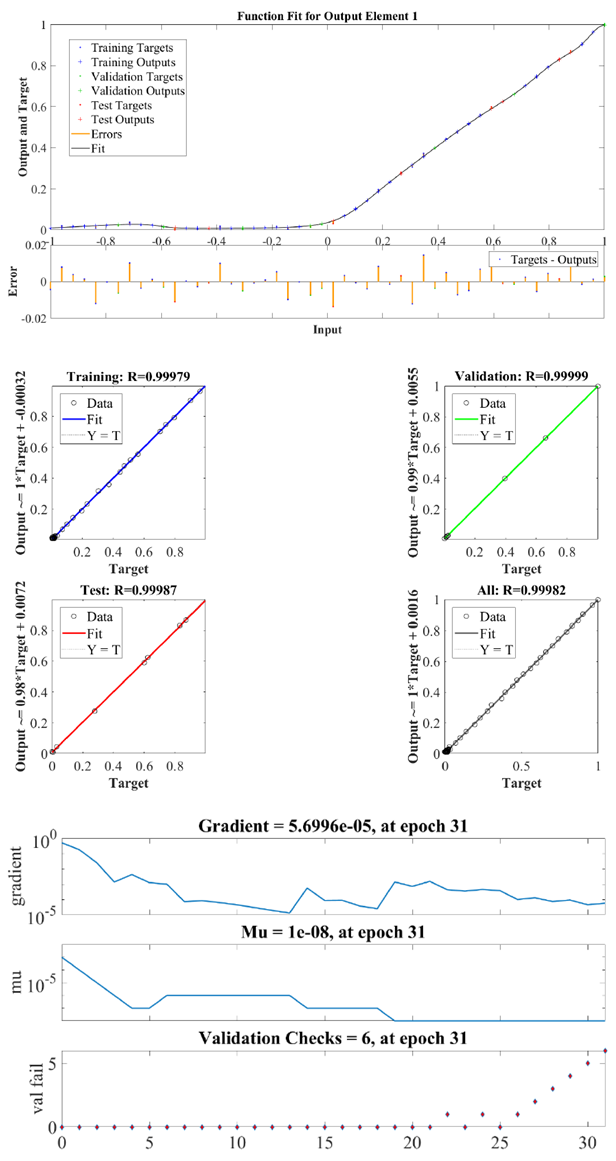 | Figure 7. Function fit (upper) and regression behavior (middle) and network performance (lower) for R function in 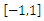 with 100 nodes with 100 nodes |
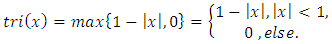 On the other hand, the triangular function is defined as the convolution of the rectangular function with itself, i.e.,
On the other hand, the triangular function is defined as the convolution of the rectangular function with itself, i.e.,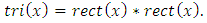 Therefore,
Therefore,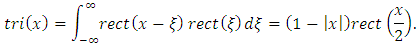 Using the relation between the rectangular and Heaviside functions, it is possible to express the triangular function in terms of the Heaviside function. More specifically, since
Using the relation between the rectangular and Heaviside functions, it is possible to express the triangular function in terms of the Heaviside function. More specifically, since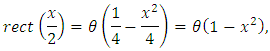 by virtue of the trivial equality
by virtue of the trivial equality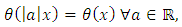 then
then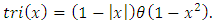 The numerical comparison of the interpolation of the tri function by means of Lagrange interpolating polynomial and artificial neural networks is shown in Figures 8-10. Figure 9 shows that when we consider 50 nodes within
The numerical comparison of the interpolation of the tri function by means of Lagrange interpolating polynomial and artificial neural networks is shown in Figures 8-10. Figure 9 shows that when we consider 50 nodes within 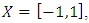 the quadratic error between the Lagrange interpolating polynomial and artificial neural network interpolation dramatically decreases up to 10th epochs. From 6th epoch on, the quadratic error remains almost unaltered and is of
the quadratic error between the Lagrange interpolating polynomial and artificial neural network interpolation dramatically decreases up to 10th epochs. From 6th epoch on, the quadratic error remains almost unaltered and is of 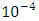 order.
order.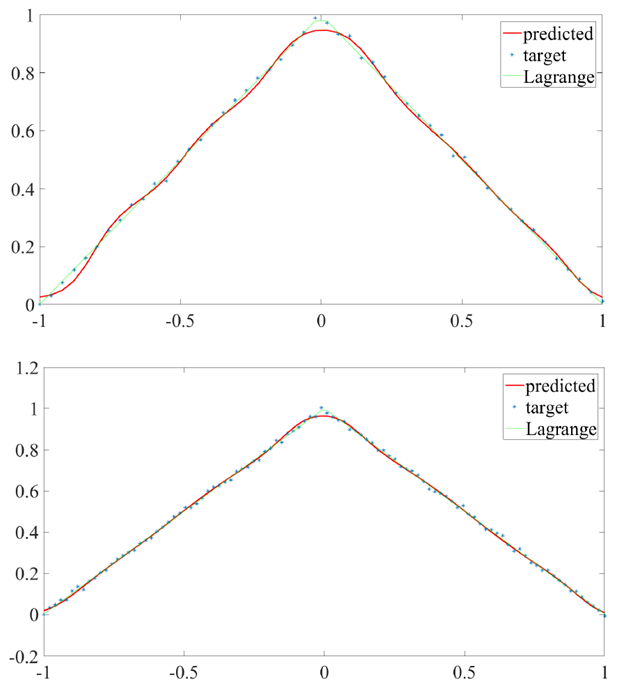 | Figure 8. Approximation of triangular function in 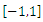 with 50 nodes (upper) and 100 nodes (lower): ANN algorithm requires 12 and 30 iterations, respectively with 50 nodes (upper) and 100 nodes (lower): ANN algorithm requires 12 and 30 iterations, respectively |
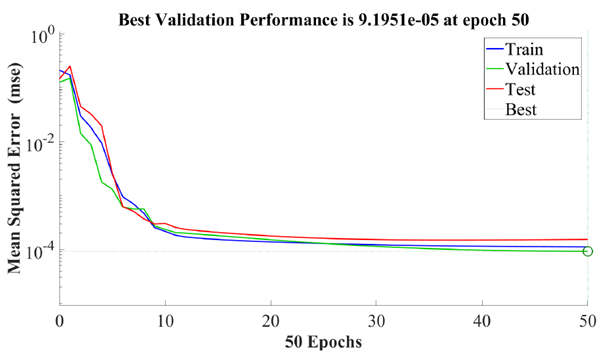 | Figure 9. Quadratic error approximation of triangular function in 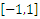 with 100 nodes with 100 nodes |
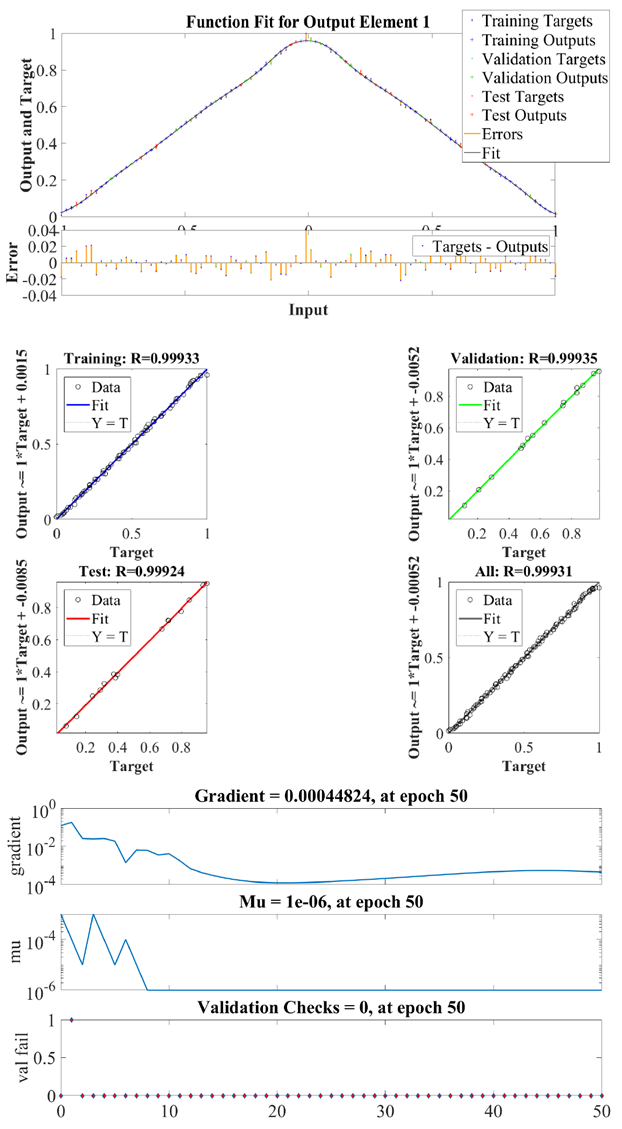 | Figure 10. Function fit (upper) and regression behavior (middle) and network performance (lower) for triangular function i 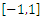 with 100 nodes with 100 nodes |
5. Conclusions
- In this paper we have studied the possibility of involving a computational neural network with a single hidden layer trained to interpolate functions with minimal number of nodes. The neural network is trained to start with the first several nodes and predict the proceeding nodes using the nearest-neighbour algorithm. The interpolation provided by the artificial neural networked has been compared numerically with the Lagrange interpolating polynomial. The algorithm is tested for the rectangular, ramp and triangular functions. It is observed that the quadratic error between the two interpolating methods dramatically decreases when the number of epochs is increased.
Notes
- 1. For the sake of simplicity, we restrict ourselves by the one-dimensional case. Higher dimensional (multivariate) cases are treated in the same way.2. Again for the sake of simplicity we consider real-valued functions. Complex-valued functions can be considered similarly.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML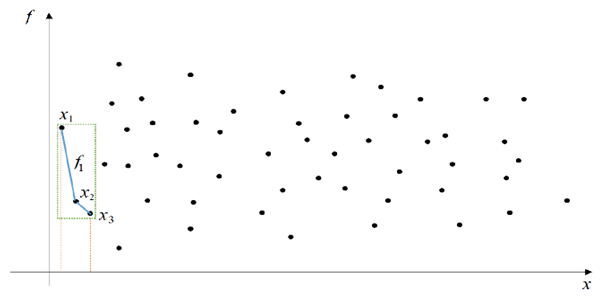
 Dashed lines draw the boundary of the first splitting
Dashed lines draw the boundary of the first splitting 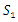 consisting of
consisting of 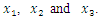 Piecewise constant (linear) interpolation is used to construct
Piecewise constant (linear) interpolation is used to construct 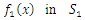 . All other interpolating functions are constructed similarly
. All other interpolating functions are constructed similarly