1. Introduction

Location problems include an extensive class of mathematical operations research models, which is interesting both actually and from the point of view of the combinatorial optimization theory [1, 2]. The aim of the location problems is the selection of one or multiple locations among candidate location in order to optimize economic indicators based on customers demand. Competitive facilities location problem is a kind of the location problems about commercial facilities and including localization of one or more facilities that after entering the market, the facility or new facilities have to compete for conquering the market with pre-existing facilities or in the future will enter the market [3, 4]. A person, who wants to open a new facility, should also consider the reaction of his competitor and use it in his decision. These issues described in the context of games theory as Leader - Follower game or Stackelberg game [5, 6].

Bi-level optimization was first realized in the field of game theory by Stackelberg who published Market Structure that described this hierarchical problem. The strategic game described in his book came to be known as Stackelberg game that includes a Leader and a Follower, and the players of the game compete together, such that the Leader makes the first move, and then the Follower reacts optimally to the Leader’s action [7, 8].

According to Stackelberg economic model, the goal of location problems of Leader and Follower find the optimal strategies for the two competitors that have sequential decision-making. Suppose, in the simplest case, there are only two decision makers, and then it is created a Bi-level hierarchical model.

Because of the NP-hardness of bi-level programming problem [9, 10], suggested Researchers several accurate algorithms for solving it [11, 12]. Li and et al. developed a new algorithm based on PSO for solving bi-level programming problem to solve the upper-level and lower-level programming problems [6, 13].

Bi-level optimization is a particular type of optimization where one problem is nested within another. Generally, the outer optimization is referred as the upper level task, and the inner optimization is referred as the lower level task. A general formulation of bi-level optimization problem can be written as follows:

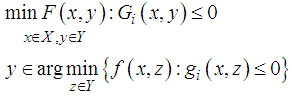Where F and f represent the objective function at the upper and lower levels respectively. x represents the upper level decision vector and y represents the lower level decision vector. G_i and g_j represent the inequality constraint functions at the upper and lower levels respectively [14].

Competitive facility location problem (CFLP) is suggested by the Hotelling in 1929 [15]. Until the 1980s is competitive facility location becoming a significant research direction of location problems. The earlier researchers mostly centralize on the models and algorithms of CFLP. Hakimi [16] assumed that there are two kinds of facilities: one is the kind of facilities which has already located, and the other is that which will be located in the future.

Lately, there are an increasing number of the elements of CFLP. Serra and ReVelle [17] suggest a successive game for a retail firm, which enters into a spatial market with one competitor that has multiple sales and produces a single product. The new user Leader firm tries to maximize its profit by finding the outlet locations and anticipates the response of the Follower that can alter the buying price of its product. Due model considered here are customers buy from the firm which the buying price and the transportation cost is the lowest. If both companies are the closest, then all of the demand is captured by the existing facility. For the solution of their problem, the authors suggest a tabu search algorithm.

Zhang et al. [18] studied the methods of benefit allocation in the process of competitive location; Fischer [19] formulates two bi-level models: a mixed-integer nonlinear bi-level model which competitor fix their locations and prices and a linear bi-level model where price variable. A heuristic solution developed to solve the linear bi-level model.

Plastria and Vanhaverbeke [20] consider the maximal covering model and incorporate into this model the information that a competitor will enter the marketplace with a new facility in the future. The aim of the Leader is to locate facilities under a budget constraint in order to maximize the market share after the competitor’s entry. The writers formulate three models corresponding to three strategies: the maximin strategy, the minimum regret strategy, and the Stackelberg.

Takeshi et al. [21] studied a CFLP with fuzzy random demand. As the CFLP is a NP-hard problem, the researchers have paid more attention to the algorithms of CFLP. Guan et al. [22] proposed a greedy algorithm and approximate search algorithm to solve this problem.

Nasreddine et al. [23] suggested a competitive facility location and design with reactions of competitors already in the market also competitive facility location problem is studied in [24, 25], in the case of free choice by the Follower of a facility to serve the user. That model assumes that the Follower makes a decision on the choice of a facility to serve each captured consumer.

Capacitated facility location problem (CFLP) is a well-known combinatorial optimization problem with applications in distribution and production planning that is classified as an NP-Hard problem. The aim is to determine where to locate facilities and how to move commodities such that the customers’ demands are satisfied and the total cost minimized [26, 27]. In the above studies, the service capacity of the new facilities is unlimited, in another word, the new facilities could service many customers with unlimited potential. In real terms, the number of real customers serviced by each facility in a period of time is limited. So the service capacity of a facility must be considered. The CFLP with considering service capacity is studied in this paper.

In this article, a new mathematical model is been suggested for competitive facilities location based on serving capacity which each competitor seeks to maximize its profit from the market share. It is assumed that facilities can choose a customer due to more profit or they don't meet consumer demand due to capacity constraint. This assumption is based on real world and can orient Problem when the total capacity of all facilities is less than the demand of all customers. Then it can provide situations to make decisions about customers who have a negative profit (cost of providing demands is greater than income). On the other hand, in this model, considered facilities attractive based on distance criteria namely closer facility is main priority to the customer. Overall, this assumption makes the model is able to define the conditions, to determine the number and location of the new facilities, also determine coverage customers. A hybrid algorithm is used to solve this problem which an exact method combined with genetic algorithm. Based on the Bi-level model, its low level is solved by the exact method and gives an exact value but overall, the first level optimization process by the genetic algorithm and obtain approximately optimization solution for all models. The algorithm is fully respects the principle of bi-level.

The decision making process for proposed algorithm can be showed as the following three steps:

1. The Leader firm creates its facilities of feasible sites of their location subject to the information that the Follower firm can also create its facilities and capture some of clients.

2. The Follower firm, informed about the open facilities of the Leader firm, creates its facilities at the locations not occupied by the create facilities of the Leader firm.

3. Each client having information about the set of create facilities of either firm chooses a serving facility based on his policies and returns interest either to the Leader firm or to the Follower firm.

This paper is organized as follows: In section 2, the suggested model is proposed and its solution process with the proposed genetic algorithm is presented in section 3. In section 4, an example is described and also presents the results of computational experiments displaying the possibilities of the suggested algorithms. Finally, the concluding remarks are made in Section 5.

2. Proposed Model

In this section, the first we will describe competitive capacitated facilities location problem with two firms in the market and then provide a Bi-level mathematical model for Leader and competitor firm (Follower) who are now in the market. The Leader and Follower firms intend to establish some facilities among some candidate points and compete to gain maximum benefit with each other. In this problem it is assumed that Follower is an intelligent person and Leader, with respect to Follower consciousness, tries to have the best performance. Follower Firm chooses number of the candidate points to set up facilities and Effect of follow behavior by 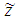variable Transferred to the Leader.

So far, in past researches have assumed that the demand points will always prefer to choose the nearest facilities, but in this paper, we assume facilities can select customers based on serving capacity and maximum benefit obtained by customers after demand of the customer to the sightly facility. In fact, based on limited capacity, facilities prefer choose the most profitable customers and they aren't responsive to the demand of least profitable customersn and thus to facility has typical right to choose between the customer. It should be noted that in this model demand delivery and so transportation costs in place is assumed and therefore, the transportation costs to the demand's location beside to their income can be effect on the selected location for facility. The purpose of this paper is to determine the optimal number and location of new facilities and customers allocation to these locations in order to maximize the profit of the Leader firm. Also in this proposed model shown customers are covered by every facility. To solve the problem; we used composition of genetic algorithm with an exact method.

Before modeling, the index sets, the parameters and decision variables of the model are defined as follows:

Indices:

I= {1,2,…,m} : an index for candidate facility points;

J= {1,2,…,n} : an index for demand points;

Parameters:

p_ij is the income realized by facility i opened by the Leader when serving client j;

q_ij is the income realized by facility i opened by the Follower when serving client j;

f_i is the fixed cost of the Leader for opening facility i;

g_i is the fixed cost of the Follower for opening facility i;

w_j is demand of customer j;

lc_i is capacity of facility i for the Leader;

fc_i is capacity of facility i for the Follower;

d_ij is distance of demand points j from location i;

dc_ij is Transportation cost from location i to demand points j

M is a big number

Decision variables:

By using the above variables and parameters, the proposed mathematical model is formulated as follows: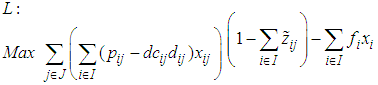

(1)

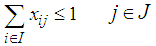(2)

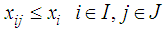(3)

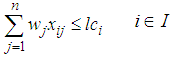(4)

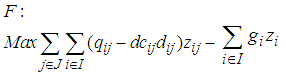(5)

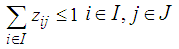(6)

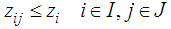(7)

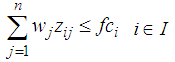(8)

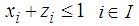(9)

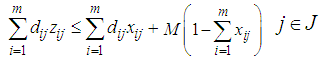(10)

As any problem of bi-level mathematical programming, the stated (1)–(10) includes the upper-level optimization problem (1)–(4) and the lower-level optimization problem (5)–(10). We will denote the upper level problem by L and the lower level problem by F.

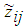The first level consists of Leader behavior that is depend on second level behavior by . The Leader intends to put their facilities in locations to gain maximum benefit even with the best Follower performance to place facilities.

The objective function (1) and (5) of the problem respectively expresses the value of the profit realized by the Leader and Follower. The constraint (2) guarantees that each client can allocate maximum one facility of the Leader; and the inequality (3) means that client can use the existing facilities of the leader in i point only when a facility is made in that point. The constraints (4) realize the amount of the leader's i facility service should not be more than the capacity of the facility. The constraints of the Follower problem (6) - (8) can be treated similarity with constraints of the Leader problem (2) - (4). The constraint (9) guarantees that maximum one of Leader or Follower facilities can be placed in i point. The constraint (10) indicates that if a customer has chosen by one of the Leader facilities but Follower established closer facility, so he can obtain the customer for own, but if Leader facility was closer, then customer surely demand supply of it facility.

3. The Proposed Algorithm

In most cases, we can solve Bi-level models by using traditional methods. Algorithms to solve Facility Location Problems (FLP) optimally suffer from combinatorial explosion and resources required to solve such problems repeatedly as required in practical applications become prohibitive. In these cases heuristic methods are the only viable alternative. We used Genetic Algorithms (GA). Therefore here for solving proposed model, we combined genetic algorithm with an exact method. In this algorithm, the role of exact method is obtain the best location for Follower problem during a process which genetic algorithm uses it to optimize the Leader model. In this algorithm the software pack of GAMS optimization problem solving and its CPLEX solver are replaced to the exact method.

Genetic Algorithm derived from nature and natural selection phenomena. First time, the algorithm introduced by Haland [28] and used to solve the complex problems. Although to obtained objective function value of the Leader, we need optimal value of Follower and subsequently optimal value of Leader models instead of his intended locations to establish facilities. To obtain objective function value in Leader problem, this problem must be resolved any time for each selected point by Leader.

The benefit of using this algorithm is with test a few points into solution space, its goes to optimal point or near to optimal. These steps are spent based on the number of iterations and finally it shows the best value as the optimal or near optimal solution. Then we will describe how solution representation and operators of the genetic algorithm to develop the proposed bi-level model.

3.1. Solution Representation

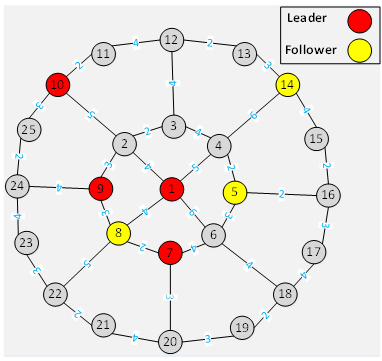
The first step to solving a problem using a genetic algorithm is how Determine solution representation which is one of the most important factors affecting on performance as well. Often Solution representation in the genetic algorithm is based on strings of Binary, correct and real numbers and set how made crossover and mutation operators based on it [29].

In the proposed algorithm, we used from a string with size of customer number for display the solution. According to how display solution, placing number i into place j means jth customer allocation to the potential place i in the Leader model. For example, in Figure 1, customer 9 allocated to the potential facility 5. Obviously, if no customer didn’t allocate to a location so facility doesn't established in that location. So if a customer allocate to facility 0 so it means dissatisfaction of customer demand. For example, in Figure 1, among the potential locations, selected locations correspond to the numbers 1, 2, 3, 5 and 9 for establish facility.

Figure 1. Solution representation in proposed algorithm

3.2. Initial Population

The second step to implement a genetic algorithm on a problem is generate a set of initial solutions called the initial population which only conducted at the beginning of the algorithm and constituted the first generation. Number of initial solutions is called population size. Population size is one of the important parameters in the genetic algorithm. Because if it is too small, the possibility that the algorithm has a good solution would be reduced, and if is too large, calculation time increases sharply to reach a good solution [30].

It is compared solution recovery against increasing solve time instead of increasing population size in sensitivity analysis to obtain best value of problem. To be effective in all initial population, it should include feasible solutions to the problem. Limited production capacity cause difficult feasible initial population for this model. Therefore, the algorithm 1 is used to generate initial solution.

Algorithm 1: the generate initial solution for proposed model

Step 1: First, a number of potential locations are randomly selected and customers are randomly assigned to them and also the demand-dissatisfaction option.

Step 2: All locations are considered and if a demand allocated to a location is greater than its capacity, go to step 3, the algorithm ends.

Step 3: The customers allocated to the facilities with violated capacity are extracted.

Step 4: The customers are randomly selected until the capacity constraint of the facility is satisfied. Also, if there is extra capacity in other established facilities, such capacity is given to the closest facilities; otherwise, their demand is not satisfied. (It is allocated to location ‘0’)

Step 5: Go to step 2.

3.3. Fitness Evaluating

The genetic algorithm uses a criterion for evaluating solutions quality and their fitness for the decision about removal or used in next generations. It takes place to preserve and pass attributes that improve the objective function of a solution. In most cases, the objective function can be a fitness criterion for algorithm solutions. In this algorithm, we used the objective function of Leader model to measure the fitness of the population members which it is penalize with a large negative number when there is a non-feasible solution. Common variables in both models with different purposes can distinguish Bi-level models. Objective function of Leader model involves a variable whose its value is achieved by optimizing the Follower model. Therefore, in the proposed algorithm to evaluate the fitness of the population members, Follower model is solved by certain variables x_i and x_ij by using a linear solver and place optimal values of the variable z_ij obtained in objective function of Leader model. In other word, values x_i and x_ij are achieved by optimization process of genetic algorithms and other variables of the model by using a linear solver.

3.4. Selection

3.4.1. Parent Selection

We used two ways in the algorithm to select parents. 10% of parents were selected among 20% of the best current solutions and the remaining (90%) by tournament method [31]. The first method ensures that the characteristics of good solutions should be transferred to the next generation. However in tournament method, it is selection of solutions with high fitness, but to maintain dispersion of search and prevention of fast convergence of algorithm the choice method can be helpful.

3.4.2. Next Generation Selection

The mechanism of the next generation selection is done among children and parents sets of current generation based on having elite namely it is selected in term of population size among best selection and the rest will be deleted. The production process of the next generation in the genetic algorithm takes place through the applied crossover and mutation operators on selected parent. We will describe the applied operators in the proposed algorithm as following.

3.5. Genetic Operators

The process of next generation production of genetic algorithms takes place through the use of combination and mutation operators on the selected parents. In following, the operations that has been used in the proposed algorithm is described.

3.5.1. Crossover Operator

Crossover operator combines characteristics and attributes of both parents. Used different crossover Operators in terms of their symmetry in various problems [30, 31]. Operators are more efficient for algorithms which during combination of parents characteristics, product the feasible solutions. As previously mentioned, display of solution has great influence on using the operators. The proposed algorithm consists of three uniform, single and two-point crossover operators with equal probability namely probability creation of a child with any of these operators is same. For more information on the operators used, the reader can refer to reference [29]. While based on display of solution, use of these operators can guarantee satisfaction of constraints (4) but there is possibility of violating the capacity constraint in children. So we can use a similar algorithm to generate initial population algorithm (algorithm 1) for restoration of the children solution. This is done by checking whether capacity of all facilities is responsive of customers. If the facility capacity has been violated, we implement steps 3 to 5 in Algorithm 1 on it.

3.5.2. Mutation Operator

The used of mutation operator to avoid the premature convergence and escape from local optimums in a genetic algorithm. This operator is used to maintain good properties that may exist only in the part of a parent solution. Usually children produced with this operator are less than the crossover operator. First in Mutation operator of the proposed algorithm, a parent is quite uniformly chosen from current generation then facility of a customer will be changed randomly. In this way, it is assigned to other facility or demand is rejected. However, the facility capacity may be violated. After mutation operator, that is why it is necessary to implement restoration of capacity constraint on child.

3.6. Steps of the Proposed Algorithm

In this section, steps of the proposed algorithm are described in algorithm 2.

Algorithm 2: the proposed bi-level genetic algorithm

Step 1: First, the problem and algorithm parameters are determined.

Step 2: Initial population is randomly generated through setting of variables x_i and x_ij .

Step 3: Follower model is generated for a population with unknown variable such as x_i and x_ij and it can be solved by GAMS solver. Moreover, the objective function of Leader model or fitness of the population member can be obtained by the optimum value z_ij.

Step 4: The following steps are repeated until the end condition is achieved:

Substep 4.1: A member of the total population with highest fitness is selected as the best solution.

Substep 4.2: The parent solutions are selected.

Substep 4.3: Child Solutions are generated by combination and mutation on pairs of parent solutions which have been randomly chosen.

Substep 4.4: values of x_i and x_ij are obtained for the child solutions.

Substep 4.5: Follower model is solved by using GAMS solver for any child then optimal values of z_ij are determined.

Substep 4.6: Objective function of Leader model or fitness for children are calculated by optimal value of z_ij.

4. Numerical Examples and Interpretation of Results

In this section, computational results of the experiences are demonstrated for efficiency of the proposed model.

Figure 2 shows the desired problem network where nodes represent demand points set and establishment facility. For assessment of the proposed algorithm performance, we used random values for facilities capacity although there is no example about a benchmark Library in literature for the Location problems [32].

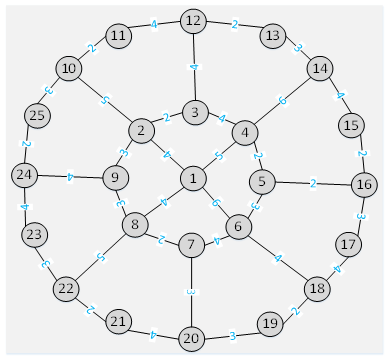Figure 2. Demand and potential points Facilities accompanied by connection network and distances

Results of algorithm in figure 3 shows that red nodes indicates selected facilities by the Leader and yellow nodes indicates selected facilities by the Follower. In this example, data is allocated and income of left points is more and the results, as can be observed in figure 3, are evidence for correct performance of model and also Leader establish 4 facilities in candidate points such as 1, 7, 9, 10 and Follower establish 3 facilities in candidate points such as 5, 8, 14. Results of the algorithm implementation showed that 90% points with highest income are covered and the rest of unselected points have long distance or high cost of potential locations establishment.

Figure 3. Algorithm performance results for example figure 2

Leader obtains optimum value in repetition 145 and benefit of the Leader firm is maximum obtained profit according to this example.

Figure 4 display convergence diagram Leader and Follower objective functions in iteration 200 and time 176.57 seconds. In this diagram Leader almost in iteration 145 reached near-optimal quantity and value of the benefit obtained for the leader, the maximum amount is due to this example has been able to obtain.

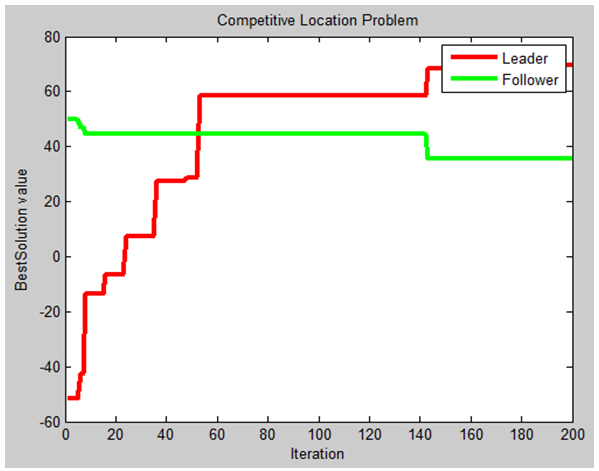Figure 4. Leader and Follower convergence diagram during solving steps with proposed algorithm

Seven examples with different sizes for display efficiency proposed model are solved and in Table 1; you can see values of the objective function, computing time and other parameters to solve problems. Factors such as transportation cost and serving capacity is also not taken into account. This problem is formulated as a bi-level linear programming model. We used accurate method with a combined genetic algorithm to solve low level in proposed bi-level algorithm. In future research, it can be considered Competition with more than two competitors then problem is converted to a multi-level model. We can consider introducing uncertainty in the attractiveness of facilities and also samples except distance in the attractiveness of facilities for the customers.

Table 1. The computational results of algorithm for problems with different dimension

5. Conclusions

In this paper competitive facilities location problem with considering service capacity where each of the competitors to attract customers and maximize their own benefit from the market share, were examined. Factors such as transport costs and service capacity are considered. It was formulated as a bilevel linear programming model. The bilevel model presented, the customer assumes the possibility of rejection by facilitating the attractiveness of facilities for customers based on proximity criteria are taken into account. Using these assumptions, the model is able to define the conditions, to determine the number and location of new facilities, customers will also determine coverage.

The proposed model solved using a new bi-level genetic algorithm. In this proposed bi-level algorithm, using an exact method that combined with genetic algorithm for solving the low level. This algorithm is fully respects the principle of bi-level. The performance of the proposed method is evaluated using numerical examples.

For future researches, competition of more competitors could be considered and the problem can be converted to a multi-level model. Introducing uncertainty in the attractiveness of the facility and cases except distance in the attractiveness of facilities for customers can be considered in the model.