1. Introduction

Convex hull (CH) is basically an important geometrical problem that could be solved computationally. The problem is all about constructing, developing, articulating, circumscribing or encompassing a given set of points in plane by a polygonal capsule called convex polygon. Justifiably, convex hull problem is combinatorial in general and an optimization problem in particular. Here, convexity refers to the property of the polygon that surrounds the given points making a capsule. A convex polygon is a simple polygon without any self-intersection in which any line segment between two points on the edges ever goes outside the polygon. Lucidly stated, a convex polygon houses a convex set which is a region such that every pair of points is within the region and the line that joins such pair is also within the region. With this definition, a cube, rectangle, regular polygon and the like are convex in nature. Any polygon which has hollowness, dent or extended vertices cannot be convex. A convex curve forms the boundary of a convex set.

Convexity of a polygon is measurable trait that is amenable to the analysis of its shape. Shape is crucial in many areas of scientific analysis such as, object classification and identification [1], biology [2], geomorphology, and powder particle characterization [3]. A vast literature survey revealed that the use of convexity measure for variety of applications such as shape decomposition [4], shape similarity measures, and object indexing [5]. The determination of convex hull of a point set has successfully been applied in application domains such as data mining [6], geographical information systems, pattern recognition [7], artificial intelligence, image processing [8] and medical simulations [9]. Apart from this, convex hull’s applications has spread in to allied areas like ray tracing, path finding, computer visualization, game theory, phase diagrams, static code analysis, verification methods, geometry, detection of outliers in statistics, rotating calipers for computing the width and diameter of a point set, digital terrain model (DTM) generation, triangulated irregular network (TIN) and area dynamic calculation [10]. Interesting enough, a special kind of application of societal interest using this wonderful concept has been in characterizing the spatial extent of animal epidemics outbreak. In this context, the spatial extent of an epidemic is assessed by computing the convex hull enclosing the infected individuals at a given time. The exact evolution equations for the mean perimeter and the mean area of the convex hull have been deduced, and the method is compared with Monte Carlo simulations [11].

At the backdrop of applications of convex hulls in various allied domains, this paper is focused to its vivid applications in the realm of image processing and pattern recognition. The objective of this paper is two folded:

• To explore the intricate applications of convex hulls in the areas mentioned.

• To enthuse the prospective research community to exploit the expanse of convex polygons as tools for newer upcoming applications.

The presentation is organized as follows; Section 2 gives an overall view of traditional approaches to the generation of convex hull. Recent methods of convex hull construction has been brought to fore in section 3,Convex hull aided image registration tasks are presented in Section 4, image classification related applications are presented in Section 5, shape decomposition shape detection, and space partitioning is the essence of Section 6. Section 7 sets the scope of the future applications of this fascinating concept, and the paper concludes in Section 8.

2. Approaches for Generation of Convex Hull

The well-known understanding about convex hull is that it is

Minimal perimeter problem for sets containing a fixed set 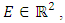and Convex hull Co(E) of E is the bounded connected set constituting a minimization problem [12].

Convex hull algorithms are broadly divided into two categories [13]:

i) Graph traversal

ii) Incremental.

The graph traversal algorithms construct CHs by identifying some initial vertices of CH and later finding the remaining points and edges by traversing it in some order. The Gift Wrapping, Graham scan, and Monotone chain are such algorithms. On the other hand, incremental algorithms first find an initial CH and then insert or merge the remaining points, edges or even sub CHs as they are discovered, into current CH sequentially or recursively to obtain the final CH. Quick hull and Divide-and-Conquer algorithms belong to this class.

The following subsections present briefly the classical algorithms mentioned above under the two categories. However, many researchers have developed various minimum convex hull development algorithms [14, 15] as an aside to the traditional algorithms.

2.1. Gift Wrapping Algorithm

The first, and the conceptually simplest convex hull algorithm is due to R. A. Jarvis [16], who published it in 1973, it has O(nh) time complexity, where n is the number of points available in the set and h is the number of points on the convex hull. This algorithm is favorable when n is small or h is expected to be very small with respect to n. In general cases, the algorithm is outperformed by many others. The algorithm gets its name owing to the way the points are processed, very similar to wrapping a string around a bundle.

The algorithm starts with a point which is on the hull, say the left most point and is the current point p_i. At each step, all other points in the set are considered and polar angles (Zenith angle or colatitudes) of the segments formed are found. Using these angles, the point p_i+1 is picked such that all the other points are to the right of the segment. Figure 1 shows the pseudo code and the graphic illustration of the algorithm.

2.2. Graham Scan Algorithm

Graham’s algorithm [17] is a sequential algorithm used to determine convex hull of a set of n points in the plane (n≥ 3). This algorithm has the complexity of O (n log n). The algorithm selects an interior point x and without loss of generality assumes that no three points of the set including x are collinear. The first step of Graham’s algorithm is to construct a sequence of the points in polar coordinates ordered about x in terms of increasing angle. It designates a point as reflex if the interior angle made by it and its adjacent points is greater than π . Figure 2 depicts the graphical illustration of the algorithm. In this figure, p₁ is non reflex and p₂ is reflex, p₂ do not entitled to be in the perimeter of convex hull. Progressively, the algorithm examines the points in the sequence in some order (clockwise/counter clockwise) and excludes those that are reflex. Upon termination, only non-reflex points remain on the periphery and remaining points will be pushed inside the hull.

Graham’s algorithm suffers a bottleneck, that when a point is abandoned for being reflex the chances are for its neighbor getting changed from non-reflex to reflex. To obviate this, modifications for this algorithm have been recommended [18].

2.3. Monotone Chain Algorithm

This algorithm is credited to A. M. Andrew [19]. As such, the algorithm is similar to that of Graham’s but with two key differences. Firstly, the algorithm sorts the points lexicographically (first by x-coordinate, and in case of a tie, by y-coordinate), and then secondly, constructs the upper and lower hulls of the points in O(n log n) time.

Iterating from left to right, the points are selected similar to Graham’s while eliminating points that contribute clockwise turns. For the upper hull iteration is carried from right to left and does the same thing. Finally, repeated left most and rightmost points are removed. The pseudo code and graphic illustrations of the algorithm are given in Figure 3.

2.4. Quick Hull Algorithm

This algorithm is based on divide-and-conquer strategy and very similar to quick sort, which divides the problem into two sub-problems and discards some of the points in the given set as interior points, on concentrating on remaining points. Under average circumstances the algorithm works quite well, but processing usually becomes slow in cases of high symmetry or points lying on the circumference of a circle. The pseudocode of the algorithm and its graphical illustration is presented in Figure 4. More detailed information may be found in [20].

2.5. Divide and Conquer Algorithm

This algorithm goes on a premise that, finding the convex hull of small sets is easier than finding the hull of large ones. Therefore, the crux of the matter here is to find a fast way to merge the small hulls that were recursively generated. While merging two small hulls, tangent algorithm is used. The tangent algorithm and its graphical illustration is shown in Figure 5. A detailed elaboration on the algorithm may be found in [21].

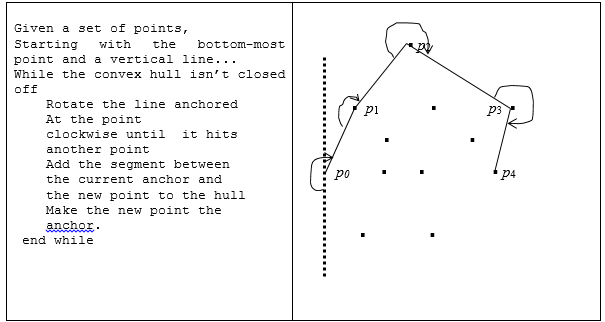Figure 1. Gift Wrapping Algorithm a. Pseudo code b. Graphic illustration

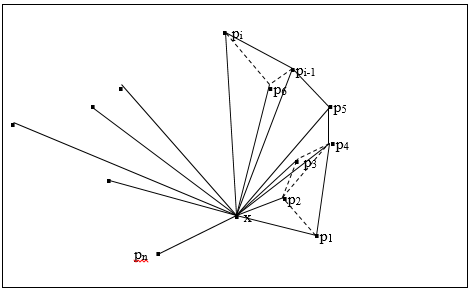Figure 2. The first step of Graham’s algorithm constructs a sequence of P= {p1, p2, …pn} of the points in polar coordinates ordered about x

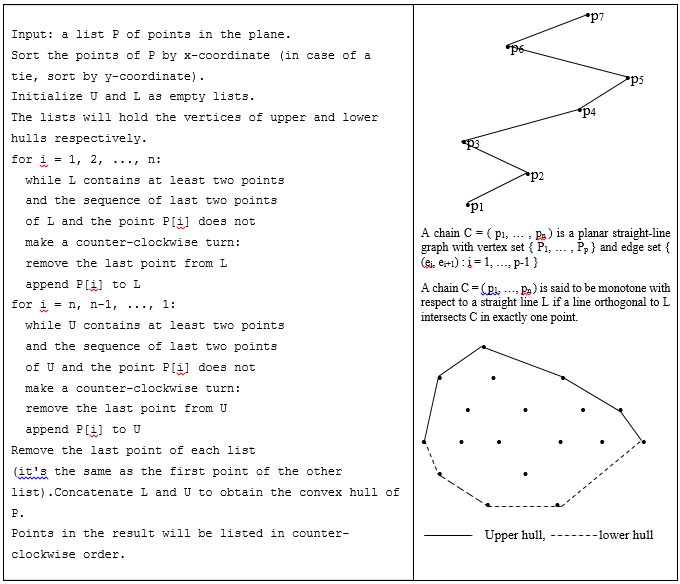Figure 3. Monotone Chain Algorithm and graphic illustration

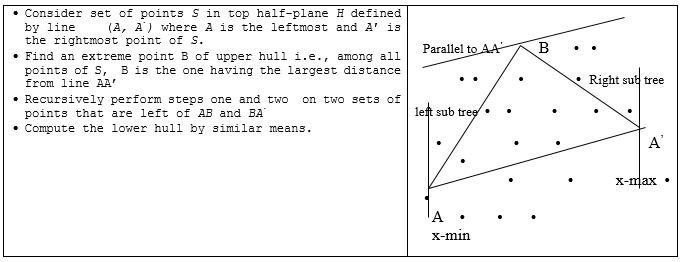Figure 4. Quick Hull Algorithm and its graphical illustration

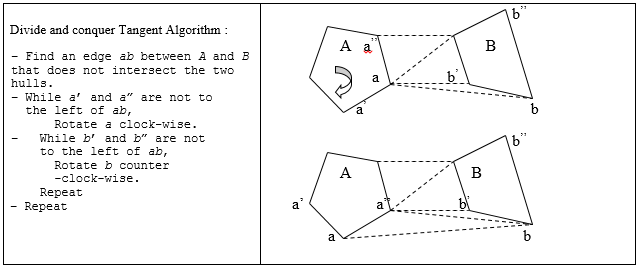Figure 5. Divide and conquer algorithm & its graphical illustration

2.6. Marriage before Conquest Algorithm

Also named as Kirkpatrick–Seidel algorithm, called by its authors the ultimate planar convex hull algorithm is an algorithm for computing the convex hull of a set of points in the plane, with O (n log h) time complexity, where n is the number of input points and h is the number of points in the hull. Thus, the algorithm is output-sensitive: its running time depends on both the input size and the output size. Although the algorithm is asymptotically very efficient, it is not very practical for moderate-sized problems. The Kirkpatrick– Seidel algorithm splits the input as before, by finding the median of the x-coordinates of the input points. However, the algorithm reverses the order of the subsequent steps: its next step is to find the edges of the convex hull that intersect the vertical line defined by this median x-coordinate, which turns out to require linear time.

The points on the left and right sides of the splitting line that cannot contribute to the eventual hull are discarded, and the algorithm proceeds recursively on the remaining points. In more detail, the algorithm performs a separate recursion for the upper and lower parts of the convex hull; in the recursion for the upper hull, the noncontributing points to be discarded are those below the bridge edge vertically, while in the recursion for the lower hull the points above the bridge edge vertically are discarded. Interested readers may go through the reference [22].

3. Recent Methods

Recent methods of computing the convex hull are directed towards accelerating the whole procedure. A recent method reported will precondition 2D data with integer coordinates bounded by a box of size p × q before building a 2D convex hull. The researchers have claimed three distinct advantages. First, they have proved that under the condition min(p, q)≤n , the algorithm executes in time within O(n). Second, no explicit sorting of data is required. Third, the reduced set of points forms a simple polygonal chain and thus can be directly pipelined into an O(n) time convex hull algorithm. They have also empirically evaluated and quantified that the speed up factor of at least four is gained by preconditioning a set of points by a method based on the proposed algorithm before using common convex hull algorithms to build the final hull [23].

The determination of the samples in the convex-hull of a set of high dimensions, however, is a time-complex task. To simplify this, a simple algorithm to compute an approximate convex hull is proposed [24]. The algorithm proposed enjoys following advantages: it uses only one threshold; it is a deterministic algorithm, independent of the vertices initially considered; it ensures that samples which correspond to maximum and minimum points for each dimension are present in the generated convex hull; and, more important, it achieves a better approximation to the real convex-hull. To apply this algorithm, the data is to be normalized in each dimension to the range [-1, 1]. All samples that have at least a minimum or maximum value for a particular dimension are selected. As a second step, a d-simplex is formed based on the first d+1 samples which are found in the first step. Afterwards, the remaining samples from the first step are incrementally appended to the convex-hull. Finally, among all samples which are located outside the current convex hull, the furthest sample to the current convex hull is selected as a new vertex and the current convex hull is updated based on the new vertex. This step is performed as long as the distance of the furthest sample to the current convex hull is greater than a pre-defined threshold.

4. Image Registration and Retrieval

Image Registration is the process of aligning two or more images of the same scene taken from different viewpoints, from different sensors, may be at different times. The purpose of image registration is to geometrically align sensed image and reference image. Registration removes or suppresses the geometric distortions between reference and sensed images. Quite a good number of applications using convex hulls has been reported in literature.

Yang et al. [25] solved the image registration and scene recognition problems in affine transformation by convex hull of corner set. This method has put forward a new idea for correspondence match of discrete features, but it is still restricted by its limitations in the field of image registration applications. It is just suit for simple scene which is easy to extract the feature contour. It requires convex hull set can reflect the feature contours of target. This requirement is clearly unrealistic for general image registration problem. But convex hull has very good properties -uniqueness for each image, affine invariant, and local controllability to occlusion or noise, which makes us have to reconsider the application of convex hull.

An improved algorithm based on convex hull vertices is proposed by Litao et al [26]. After extracting feature points by Harris corner detector, for searching the same regions of reference images, correlation method is used to match these points firstly, which gains two initial pairing sets. Then convex hull vertices of the pairing sets are used to establish the transformation parameters that can match most points of the two pairing sets, which use a convex hull using random sample consensus (RANSAC) like algorithm. Computational experiments have demonstrated the accuracy, efficiency and robust of this approach.

A novel approach to recover the parametric deformation that optimally registers one image to another has been reported [27]. The method proceeds by constructing a global convex approximation to the match function which can be optimized using interior point methods. The method used also explains how one can exploit the structure of the resulting optimization problem to develop efficient and effective matching algorithms. Results obtained by applying the proposed scheme to a variety of images are presented. The gist of the methodology used lies in recovering the deformation that maps a given base image onto a given target image can be phrased as an optimization problem. For every pixel in the target image one can construct an objective function, which captures how similar the target pixel is to its correspondent in the base image as a function of the displacement applied at that pixel.

A robust approach called convex hull matching (CHM) technique is proposed for registration of medical images that differ from each other with Euclidean transformation. The method involves two steps, in the first step, point sets on the surface of the medical image are extracted, and then the 3-D convex hull is constructed from the point sets and triangle patches on the surface of convex hulls are specified by predefining their normal vectors. Subsequently in the second step, each edge of the referenced triangle is compared with all the edges of the triangle in other point set to find the congruent pair set and also to obtain the scaling factor. Thereafter, the transformation parameters of each triangle pairs including rotation and translation are optimized by minimizing the Euclidian distance between the corresponding vertex pairs. Hence, rigid transformation of the two point sets is obtained by iteratively enumerating and evaluating similarity measures of the triangle patches chosen. Global optimization is achieved through RANSAC optimization by removing the correspondence pairs that may lead to large matching errors of the whole point sets. The real clinical data experiments have confirmed the proposed algorithm is a strong performer in medical image registration [28].

Applications of convex hull for optimized image retrieval have been scanty. In a significant effort, a new image retrieval method based on region of interest determined by interest points has been cited [29]. The method is about detecting interest points by tracking wavelet coefficients of different scales and computing convex hull of interest points to extract the region of interest in the image. The weighted feature distance was used to define the similarity between two images. With robustness to image rotation, translation and scale, the method makes the retrieval implementation at the object level and avoids the shortcoming of traditional methods. Quite a good number of experiments based on an image database containing 1100 images has showed improvement in the average retrieval precision over 11.1%, compared with other interest points based retrieval methods.

In the recent years, convex hulls have been immensely used for content based image retrieval. Considering the complex objects and information present in the image development of automated retrieval system is very difficult if not impossible. Such systems should cater to browsing, searching and retrieving images from a large image database. A new approach that could mitigate the above said difficulties has been reported [30]. The method involves comparing convex hull geometry of the query image to that of the database image in terms of a relative metric which is denoted as the Convex Hull Area Ratio (CHAR). The metric CHAR is the ratio of the area of the intersection of the two convex hulls to the area of their union. A polygon in the shape of the convex hull is extracted from the database images and the coordinate values are stored in the feature library. When query image is presented, the convex hull values are extracted and the ratio of the intersected area to union area of the two convex hulls (CHAR) are found and stored. Then, similarity measurement is performed and the closest match is associated with the highest value of CHAR.

Another interesting direction in computer vision related tasks has been detection of object level saliency detection. In this direction, salient features of an object are garnered by exploiting contrast, center and smoothness priors. In such an application, convex hull is applied to elicit the center of the salient object rather than directly using the image center. This strategy has shown to be more robust when compared with the method of location of objects [31]. Added to this, the method is refined by developing the initial saliency map through minimizing a continuous pair wise saliency energy function with graph regularization. This method has also enabled uniformity in highlighting the salient object and simultaneously suppresses the background effectively. Extensive experiments on a large dataset demonstrated that the method proposed by the researchers performs favorably against the state-of-the-art methods in terms of accuracy and efficiency.

5. Image Classification

Convex hulls have large potential to realize regions as a large margin classifier. Indeed, the closest point pair on the convex hulls each of which encloses all the samples of a single class gives the same liner classifier as Support Vector Machine. A practical way is proposed to find a set of approximate convex hulls in each class as an estimate of the class region. In the algorithm, training samples are perfectly separated by those convex hulls. Model selection is being made for avoiding overfitting. A model is specified by the number of facets, the number of convex hulls, and the number of irregular (too thin or too small) convex hulls. Further the concept of an expanded convex hull which produces a classifier with large margin has also been introduced [32].

A new algorithm to search the border points, called convex-concave hull has been presented [33]. For this, the convex hulls of the data set were first found. Then concave hulls are formed using the vertices of the convex hull. In this way, the misleading points in the intersection were identified to be the vertices of the concave hulls. By this algorithm, the classification accuracy is reported to have increased considerably when compared with the geometric methods also the training time is decreased substantially. The experimental results of this work showed that the accuracy obtained by new convex-concave hull approach is very close to classic SVM methods, while the training time is significantly shorter. Convex hulls have been expeditiously implemented along with Support vector machine (SVM). SVM being a statistical learning theory, capable of avoiding over-training, and weak normalization capability. However, the black-box characteristic of SVM has limited its application. In order to open the black-box, a new rule extraction algorithm based on convex hull theory is proposed [34]. In this work, all the vectors were clustered to be some clusters on the decision hyper-plane; then, the convex hull is extracted for every cluster; finally, the region of each convex hull covered were transferred to corresponding interval-type rule. Rule extraction has been experimented on two public datasets of Iris and Breast-cancer images, results have showed that the proposed method can improve the accuracy of rule covering and fidelity.

An attempt to classify the Single Proton Emission Computer Tomography (SPECT) brain images into Alzheimer disease inflicted and non- inflicted has been attempted [35]. Set of descriptors such as brain area, maximum internal sphere, its diameter, digital volume and surface was determined using the convex hull. The methodology was based on the variation of relative threshold together with relative pre-erosion. The descriptors were converted to the relative logarithmic form and the linear model of single neuron was used for the classification of brain disease.

It is prudent to mention application of convex hulls in generating the receiver operating characteristic (ROC) graph. It is well known that ROC is used for visualizing, organizing, and selecting classifiers based on their performance. It is therefore common to generate ROC curves for varying discriminative thresholds over the output of the classifier. There is spurt in use of ROC graphs in the machine learning community, thus ROC analysis has become a central technique for tackling classification problems. In this context, recently, attention has also been drawn toward the ROC convex hull (ROCCH) [36]. Consequently, there are many works on ROCCH maximization problems, most of which are geometric-based methods for maximizing the ROCCH [36]. Particularly, since ROCCH maximization means to find a group of classifiers whose location (performance) is as close to the top-left corner in the ROC space as possible, i.e., that have a high true-positive rate (tpr) and low false-positive rate (fpr), multi objective optimization techniques have been widely acknowledged as promising approaches to it. There are several works proposing different multi objective optimization frameworks based on pair-wise dominance relationships to maximize the ROCCH [37].

A new convex hull-based multi objective genetic programming (CH-MOGP) is proposed to solve ROCCH maximization problems [38]. Specifically, convex hull-based without redundancy sorting (CWR-sorting) is introduced, which is an indicator-based selection scheme that aims to maximize the area under the convex hull. A novel selection procedure is also proposed based on the proposed sorting scheme. It is hypothesized that by using a tailored indicator-based selection, CH-MOGP becomes more efficient for ROC convex hull approximation than algorithms that compute all Pareto optimal points. Empirical studies are conducted to compare CH-MOGP to both existing machine learning approaches and multi objective genetic programming (MOGP) methods with classical selection schemes. Experimental results show that CH-MOGP outperforms the other approaches significantly.

6. Shape Detection, Extraction, and Space Partition

Physiological researchers have emphasized the fact that the human visual system tends to segment complex objects at the region of deep concavities thus highlighting importance of concavities in shape detection [39]. Taking a cue from this fact, a method is proposed for measuring concavities and segmenting 2D shape without holes by convex hulls. The said method is intended to grasp variations of the polygon boundaries and to determine vertexes before computing interior angles for representing local attributes [40]. To deal with excessive segmentation, a decomposition method is introduced avoiding connection of vertices in the same pocket generated by convex hull the author has claimed good performance by the approach in shape detection. Finding optimal convex hulls for shape extraction using genetic algorithms has been presented [41]. The method proposed in this work gets shape in wrapping from convex hull. After obtaining approximate convex hulls, crossover, a local search method, and a modified fitness function are applied to get the shape in the wrapping. It is shown by the authors that the proposed method succeeds in extracting the shape from the point sets in the plane. The results of this work have shown success in acquisition of the convex hull and the shape of objects. The time involved in obtain each problem’s convex hull is reported to be within half of a second.

A method for partitioning an image database by classifying and indexing the convex hull shapes and the concavity features of regions is reported [42]. This approach has resulted in significant increase in image search and retrieval speed. In this work, the convex hull is established using a novel and efficient method based on the geometrical heat differential equation. The so obtained convex hull is represented by a triad of boundary shapes and other parameters as viewed from three viewpoints. The information about the boundary shapes has enabled the researchers to categorize the regions in image database to be captured by 344 convex hull classes. Both theoretical background and practical results are presented. Extending further, the information about concavity of the region has also been elicited using boundary support parameterization which helped the researchers for further partitions of the database. This has also resulted in comparing shapes of the same class thus reducing the searching operations.

In another practical application of convex hulls, a prototypic model for leaf and fruit classification with specific reference to Tomato has been attempted [43]. In this work, convex hulls are used to capture morphological shape based features. Later, supervised filter and wrapper based feature selection techniques were adopted to choose the optimal feature set which lead to small within-class variance and large among-class distance. This information was used as a yardstick by the recognition system. Yet another significant application of convex hull has been detection of leukemia by determining abnormal white blood cell (WBC) count [44]. In this work, convex hull of blood cells is computed to determine number of cells in an image. While traditional methods which involve manual counting of the cells under a microscope which obviously lead to errors in counts, the method developed in this work has shown better results for counting number of WBC and computing Blood Cell Ratio. Convex hull is used for detection of Glaucoma [45]. Glaucoma detection involves measurement of neuro-retinal optic cup-to-disc ratio (CDR). Automatic calculation of CDR is challenging due to the interweavement of blood vessels running in the surrounding tissues around the cup. The authors have developed convex Hull based Neuro-Retinal Optic Cup Ellipse Optimization algorithm. This algorithm has improved the accuracy of the boundary estimation by around 43% when compared with the traditional method. Around 70 clinical patients’ data base is used in the research.

Convex hull algorithm has made inroads to handwritten character detection also. Hand written texts poses at most difficulty while tracing when compared to machine written text because of their non uniformity in sizes and strokes. In a recent work, convex hull algorithm has been used to collect 125 features Bangla basic characters and digits [46]. On experimentation with database of 10000 samples, a maximum recognition rate of 77.8% in case of characters and 99.5% in case of digits has been reported. This work has validated the usefulness of new feature set availed through convex hull.

In a very innovative and interesting work, a new approach for controlling mouse movement using image processing technique. The research work makes use of image processing via Convex Hull Method and captures human hand gestures to replace mouse functions. (i.e. left click, right click, and cursor movement). For this, convex hull algorithm is used to replace the actual mouse with human hand. The shape of the hand while holding the mouse has been captured using convex hulls. To recognize that a finger is inside of the palm area or not, convex hull algorithm are once again used. The method suggested has shown excellent results while identifying finger tips on the hand and also to detect whether the fingers are folded or not [47].

7. Scoping View

The predominant task in an image processing work is shape based feature extraction. The delineable shape based features must possess following properties [48]:

Ÿ Shapes that are recognized by human beings to be perpetually similar have the same features that are remarkably different from other shapes.

Ÿ Some of the rendered transformations such as translation, rotation and scaling should not alter the extracted feature values.

Ÿ Affine transformations of the shape in different coordinate systems should preserve the straightness and parallelism of lines.

Ÿ The features must be the same whichever be the strength of the noise in a given range that affects the pattern.

Ÿ When some parts of a shape are occulted by other objects, the feature of the remaining part must not change compared to the original shape.

Ÿ Two features that are retrieved out of a shape must be statistically independent.

In order to safeguard the properties cited above, a robust shape holder or shape capturing method is needed. Though copious research has shown extensive use of convex hull for shape extraction, it is neither prudent nor equitable to affirm a property of an approach by hard qualifiers as good or bad. Because certain approaches have great different performances under different conditions. A comparative analysis of various shape capturing techniques with special reference to fulfillment of above listed properties is presented in Table 1.

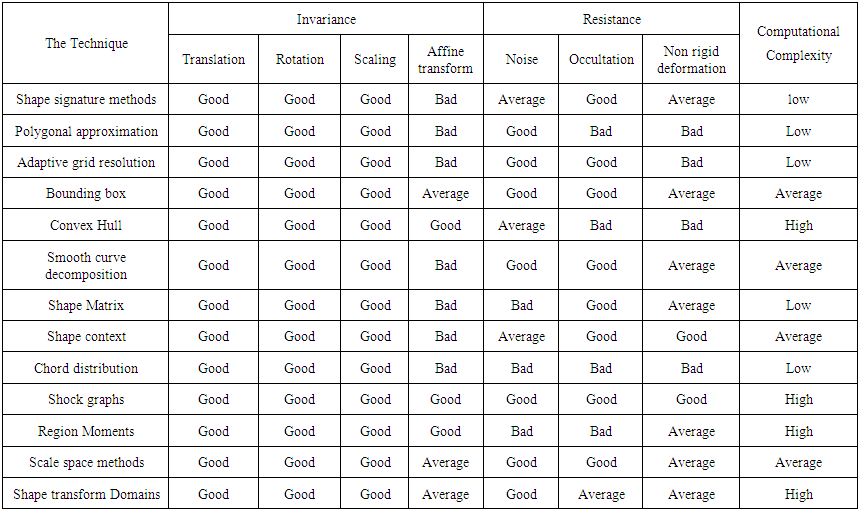Table 1. A Comparative presentation of shape extraction techniques

The impact of convex analysis in optimization is well-known and the rich and varied set of applications of convex hulls in areas such as finite convex, integration, network flow, phase transition, electrical networks, and robot navigation is very well documented in literature. Its application in image processing is rather intrinsic. Maragos [49] has established the connection between convex analysis, image processing, differential calculus and dynamical systems and conjointly named it as differential morphology. The operators used in image processing such as distance transform, dilation and regularization are closely connected to convex analysis [50]. Considering the wide applications that have happened in recent years, the future scope for convex hull applications in image processing may be listed below.

Ÿ The proposed algorithms used for classification have shown lower margin between approximate convex hulls of classes, therefore, efforts should be directed to expand the margin space preferably with user specified value.

Ÿ It is discerned from the literature that, convex hulls have shown very low classification errors mostly if small data sets are involved. However, in the case of larger data sets, the classification accuracy are not very much better than other classification methods. This suggests a scope for development of methods applicable to large datasets.

Ÿ In classification tasks associated online noised data, convex hulls are not able to adapt and it is seen in some works that the updated classifier showing deviations from the true classifier. How to eliminate the heavily noised data points in the online processes is still an intractable issue demanding future attention.

Ÿ The affine variant features garnered using convex hulls have shown low recognition rates. Researchers are of the opinion that combination of affine invariant features may improve overall recognition performance of pattern class.

Ÿ Convex hulls are prone to errors when the images are not exactly same. It is required to develop algorithms that use the affine invariant and noise insensitive convex hulls involving correlation criteria to concentrate feature points to the same region of image contents.

Ÿ There seems to be a huge scope for convex hulls in the area of content-based image retrieval. Efforts are anticipated in the direction of developing similarity metrics particularly with reference to medical images.

Ÿ Another promising scope in foreseeable future is the development of 3D-convex hulls. The research in this direction is still in gestation stage and has to take a long leap forward. It is strongly opined that such 3-D convex hulls are of immense use spatial analysis in 3D geographical Information systems [51].

8. Conclusions

In this article we have underlined the importance and significance of Convex hulls in image processing tasks. This article is also driven by the renewed demands from image processing applications such as robustness, higher recognition rates, and clear interpretations of images. Convex hull assisted image processing has been successful in image registration, image classification, shape extraction, content based image retrieval, feature selection, and space partitioning. It is felt that the prospective researchers in the area of image processing are encouraged by this article and further explore convex hull based algorithms in the future development of image processing technologies.