-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Intelligent Systems
p-ISSN: 2165-8978 e-ISSN: 2165-8994
2015; 5(3): 81-91
doi:10.5923/j.ajis.20150503.01
A Fuzzy Time Series Forecasting Method Based on Operation of Union and Feed Forward Artificial Neural Network
Eren Bas1, Ufuk Yolcu2, Erol Egrioglu1, Cagdas Hakan Aladag3
1Department of Statistics, Giresun University, Giresun, Giresun, Turkey
2Department of Statistics, Ankara University, Ankara, Turkey
3Department of Statistics, Hacettepe University, Ankara, Turkey
Correspondence to: Erol Egrioglu, Department of Statistics, Giresun University, Giresun, Giresun, Turkey.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Fuzzy time series methods do not require any assumptions valid for classic time series approaches. The most important disadvantage of fuzzy time series approaches is that it needs subjective decisions, especially in fuzzification stage. In the some fuzzy time series methods, membership values are ignored but the membership values are vital in a fuzzy inference system. In this study, a high order fuzzy time series approach was suggested and proposed approach is a method which uses membership values to obtain forecasts. When the membership values for high order fuzzy time series forecasting model are used as inputs of feed forward artificial neural network, too many inputs must be used. Because of too many inputs, the structure of artificial neural networks becomes a complex architecture and it is needed too much calculation time for too much weights and biases in the network structure. To overcome this problem, the operation of union is firstly used to combine inputs in the proposed method. In order to evaluate the performance of the proposed method, it has been applied to University of Alabama enrollment data, index 100 in stock market of Istanbul and Taiwan futures exchange data the obtained results have been compared with other fuzzy time series methods. At a result of the applications, it is seen that the proposed approach has superior forecasting performance.
Keywords: Artificial neural networks, Forecasting, Fuzzy c-means, Fuzzy time series, Operation of union
Cite this paper: Eren Bas, Ufuk Yolcu, Erol Egrioglu, Cagdas Hakan Aladag, A Fuzzy Time Series Forecasting Method Based on Operation of Union and Feed Forward Artificial Neural Network, American Journal of Intelligent Systems, Vol. 5 No. 3, 2015, pp. 81-91. doi: 10.5923/j.ajis.20150503.01.
Article Outline
1. Introduction
- Forecasting is of vital importance in determining efficient strategies for the future. For this reason, a number of scientific studies that aim to forecast time series have been put forward. Traditional time series approaches with probabilistic models require some assumptions such as number of observations, normal distribution, and linearity. Thus, these approaches can lead to misleading forecasting results when these assumptions are not satisfied. Therefore, non-probabilistic approaches have been put forward as an alternative to probabilistic time series forecasting models. In recent years, fuzzy time series approach has become prominent among non-probabilistic time series forecasting methods.Zadeh [1] formed a basis with fuzzy set theory which was put forward by own for fuzzy time series approaches which was firstly proposed by Song and Chissom [2]. Song and Chissom [2] introduced fuzzy time series in two parts as time-variant and time-invariant. In this study, it has been focused on time-invariant fuzzy time series. Fuzzy time series forecasting models consist of three stages. All these stages play an active role on the forecasting performance. These stages are; fuzzification, determination of fuzzy relations and defuzzification, respectively.In fuzzification stage, despite the use of partition of the universe of discourse, more systematic approaches have been put forward in recent years. The first studies in this stage, equal intervals lengths were determined arbitrary in the studies of Song and Chissom [2-4] and Chen [5, 6]. Huarng [7] proposed two different approaches based on mean and distribution. These approaches have shown the role of interval lengths on the forecasting performance. Egrioglu et al. [8, 9] determined equal length intervals based on optimization, in this stage. Besides, Huarng and Yu [10] suggested an idea that the partition of universe of discourse was determined with changing of sub-intervals based on ratio. Yolcu et al. [11] proposed an approach to optimize this ratio. Separately to determine the dynamic length of interval, Davari et al. [12], Kuo et al. [13,14], Park et al. [15], Hsu et al. [16], Fu et al. [17] and Huang et al. [18] utilized particle swarm optimization technique, Chen and Chung [19] and Lee et al. [20, 21] also utilized genetic algorithm. All of these approaches examined carefully it is clearly seen that a more systematic structure occurs gradually in fuzzification stage.However, the membership values of fuzzy observations were determined subjectively in first studies. In order to eliminate this problem, Cheng et al. [22] and Li et al. [23] used fuzzy C-means (FCM) clustering technique; Egrioglu et al. [24] used Gustafson-Kessel fuzzy clustering technique in fuzzification stage.The stage of determination of fuzzy relation is a stage that the inner-relation of fuzzy time series is determined in this stage. Therefore, this stage is highly important because of finding the proper model and thus this stage provides a major contribution to obtain superior forecasting performance. Song and Chissom [2-4] used fuzzy logic relation matrix in this stage. Sullivan and Woodall [25] used transition matrices based on Markov chain instead of using fuzzy logic relation matrix. Chen [5] proposed a simplified approach with the idea of matrix calculations are based on complex operations. This approach used fuzzy logic group relationships tables to determine the fuzzy relations. Huarng and Yu [26] proposed a first order fuzzy time series approach using feed forward artificial neural network (FFANN) in this stage. Besides, Aladag et al. [27] developed the method of Huarng and Yu [26] and proposed a high order fuzzy time series forecasting model. During the determination of fuzzy relations, the membership values have been ignored and index numbers of fuzzy sets have been considered in all of these approaches. This situation may cause lack of information and it may affect the forecasting performance, negatively. In order to eliminate this problem, Yu and Huarng [28] proposed an approach considering all memberships to determine the fuzzy relations. But Yu and Huarng [28] also determined these membership values subjectively. To solve this problem Yolcu et al. [29] proposed an approach. According to this approach all memberships were determined by FCM technique instead of the study of Yu and Huarng [28]. Despite their superior properties of these two methods, they contain only first order fuzzy time series forecasting model. However, it will be more suitable using high order models instead of first order models for forecasting of fuzzy time series with a more complex structure relation. Therefore, the methods proposed by Yu and Huarng [28] and Yolcu et al. [29] can be transformed into a high order model structure. But this situation will lead to a problem that the number of input of artificial neural network will increase too much. In such a case, the training of the network takes a long time, the training of network becomes more difficult and also its superior forecasting performance may affected, negatively. In defuzzification stage, many researchers such as Chen [5], Huarng [7] and Huarng and Yu [10] used centroid method. Song and Chissom [4] used ANN in this stage and Cheng et al. [22] and Aladag et al. [30] preferred to use adaptive expectation method. Yolcu et al. [29] proposed an approach considering all membership values in this stage.In this study, a high order fuzzy time series approach using fuzzy c-means clustering method in fuzzification stage and considering all the membership values in the stages of determination of fuzzy relations and defuzzification stage has been proposed. Thus, a more systematic approach that uses more information has been proposed. In addition, in the stage of determination of fuzzy relations the problem of the too much input number of artificial neural network with multiple inputs and multiple outputs has been solved by using operation of union. The proposed method has been applied to different time series used in the literature and the results have compared with some other fuzzy time series methods.
2. Overview of Related Techniques
2.1. The FCM Clustering Technique
- FCM clustering technique has been used especially in recent years in fuzzification stage of the fuzzy time series forecasting methods. The FCM clustering technique was firstly introduced by Bezdek [31]. This clustering technique is the most widely used clustering algorithm. In this technique, fuzzy clustering is conducted by minimizing the least squared errors within groups. Let uij be the membership values, vi be the center of cluster, n be the number of variables, and c be the number of clusters. Then the objective function, which is tried to be minimized in fuzzy clustering, is
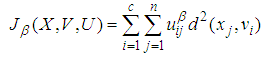 | (1) |
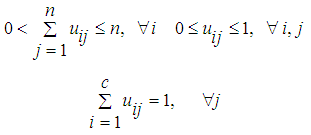 | (2) |
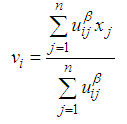 | (3) |
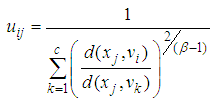 | (4) |
2.2. Artificial Neural Network
- Artificial neural networks can be defined as the mathematical algorithm that is inspired by the biological neural networks. Artificial neural networks, defined as the mathematical algorithms, are the algorithms that can learn from the examples and that can generalize what is learnt. Network presentation is the graphical expression of mathematical algorithms. Artificial neural networks are much more different than biological ones in terms of their structure and ability [32]. Artificial neural networks compose of a mathematical model [33].Three basic components that direct the operation of artificial neural networks are as follows;Architecture Structure: The architecture structure of multilayer feed forward artificial neural network consists of input layer, hidden layer(s) and output layer (see Figure. 1). Each layer consists of neurons. The architecture structure is determined based on deciding the number of neuron in each layer. These neurons are linked each other by weights. There is no link among the neurons in the same layer.
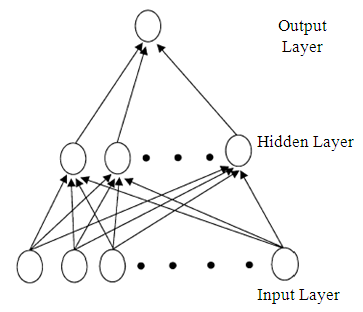 | Figure 1. Architecture of multilayer feed forward neural network |
2.3. Basic Definitions and Concepts Related to Fuzzy Time Series
- The fuzzy time series was firstly defined by Song and Chissom [2]. The basic definitions of fuzzy time series, and time variant and time invariant fuzzy time series definitions are given below.Definition 1 Let Y(t) (t = …, 0, 1, 2, …), a subset of real numbers, be the universe of discourse on which fuzzy sets fj(t) are defined. If F(t) is a collection of f1(t), f2(t), … then F(t) is called a fuzzy time series defined on Y(t).Definition 2 Suppose F(t) is caused by F(t – 1) only, i.e., F(t – 1) → F(t). Then this relation can be expressed as F(t) = F(t – 1) R(t, t – 1) where R(t, t – 1) is the fuzzy relationship between F(t – 1) and F(t), and F(t) = F(t – 1) R(t, t – 1) is called the first order model of F(t). " " represents max-min composition of fuzzy sets.Definition 3 Suppose R(t, t – 1) is a first order model of F(t). If for any t, R(t, t – 1) is independent of t , i.e., for any t , R(t, t – 1) = R(t – 1, t – 2), then F(t) is called a time invariant fuzzy time series otherwise it is called a time variant fuzzy time series.Song and Chissom [2] firstly introduced an algorithm based on the first order model for forecasting time invariant F(t). In Song and Chissom’s [3] labour, the fuzzy relationship matrix R(t, t – 1) = R is obtained by many matrix operations. The fuzzy forecasts are obtained based on max-min composition as below:
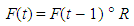 | (5) |
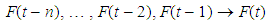 | (6) |
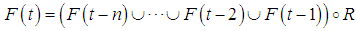 | (7) |
3. The Proposed Method
- Each stage of fuzzy time series approach is highly effective on the forecasting performance of the method. Therefore, there are many studies on these stages in the literature. The main purpose of researchers is to make the methods more systematic and to present more suitable approaches for the fuzzy set theory. For this purpose, Cheng et al. [34] and Li et al. [23] used FCM clustering technique; Egrioglu et al. [24] used Gustafson-Kessel fuzzy clustering technique in the fuzzification stage. In these methods, the partition of universe of discourse was not used in fuzzification stage and the membership values were not determined with a systematic approach. The stage of determination of fuzzy relation can be considered as the most important determinant of the forecasting performance of the model since the inner-relations of fuzzy time series are determined in this stage. In almost all studies available in the literature, the membership values are ignored in this stage. This situation may affect the forecasting performance negatively since ignorance of membership values cause lack of information. Yu and Huarng [28] proposed an approach that considers all membership values to determine the relations with FFANN but these membership values were determined subjectively. In order to eliminate this problem Yolcu et al. [29] proposed a new approach. In this approach, the membership values were determined with FCM technique and all membership values were taken into consideration. Although fuzzy time series forecasting models which were proposed by Yu and Huarng [28] and Yolcu et al. [29] have important advantages, these models were only first order forecasting models. On the other hand, it is usually necessary to use high order models since many time series encountered in real life contains complex relations. To forecast such time series, high-order fuzzy time series forecasting models should be utilized. In high order models, the increment of the input number of FFANN is a crucial problem. In the first order models, the number of FFANN inputs is number of fuzzy sets while the number of FFANN inputs is product of number of fuzzy sets and model order in the high order models. Therefore, the number of inputs can be too much in the high order models. In such a case, training of a network will take a quite long time as well as gets difficult so the performance of forecasting will be affected negatively. By the method proposed in this study, it is aim to forecast of time series which contains high order fuzzy relations. The proposed method avoids subjective decisions by using FCM technique in fuzzification stage and the proposed method also presents an approach using FFANN in the stage of determination of fuzzy relations and takes all membership values into account in defuzzification stage. The proposed method has some important advantages which can be summarized as follows:• There is no require to partition of universe of discourse in fuzzification stage and memberships are determined based on a systematic method by using FCM.• Operation of union has been applied to all fuzzy lagged variables to overcome the problem that is too much input for artificial neural network models.• The proposed approach is in accordance with the fuzzy set theory since this approach takes all membership values into consideration in the stages of determination of fuzzy relations and defuzzification. Therefore, information loss is avoided and an increase in the explanation power of the model is provided.• The proposed method is considerably suitable for forecasting of time series with complex relations since it is based on high order fuzzy time series forecasting model.• As a result of the advantages of the proposed method given above, it is clearly expected that the method has high forecasting accuracy.The algorithm of the proposed method is given below step by step.Step 1 Fuzzify observations of time series by using FCM clustering method.Let c be the number of fuzzy sets, such that
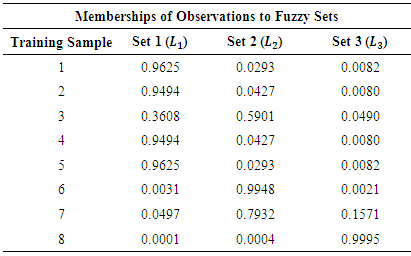
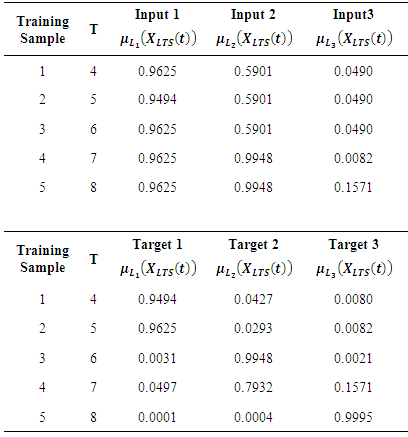
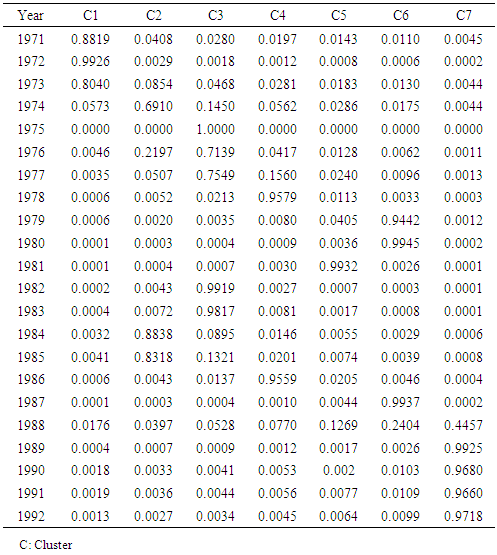
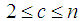 where n is the number of observations. FCM clustering algorithm in which the number of fuzzy sets is c is applied to the time series consists of crisp values. Then, after the center of each fuzzy set is determined, the degrees for each observation, which denote a degree of belonging to a fuzzy set for that observation, are calculated with respect to the obtained center values of fuzzy sets. Finally, ordered fuzzy sets Lr (r=1,2,…,c) are obtained according to the ascending ordered centers, which are denoted by vr (r=1,2,…,c).Step 2 Define the fuzzy relationship with FFANN.The number of neurons in the input and output layers of FFANN is equal to the number of fuzzy sets, c. The numbers of neurons in the hidden layer are decided via trial and error. In this process, the point to take into consideration is to avoid a possible loss in ability of generalization of the feed forward neural network. The inputs of FFANN consist of membership values and these membership values are obtained by applying operation of union to the vector of membership values of observations of each lagged time series. For example, we consider three order fuzzy time series forecasting model. Let the number of fuzzy sets be three. The membership values are given in Table 1.
where n is the number of observations. FCM clustering algorithm in which the number of fuzzy sets is c is applied to the time series consists of crisp values. Then, after the center of each fuzzy set is determined, the degrees for each observation, which denote a degree of belonging to a fuzzy set for that observation, are calculated with respect to the obtained center values of fuzzy sets. Finally, ordered fuzzy sets Lr (r=1,2,…,c) are obtained according to the ascending ordered centers, which are denoted by vr (r=1,2,…,c).Step 2 Define the fuzzy relationship with FFANN.The number of neurons in the input and output layers of FFANN is equal to the number of fuzzy sets, c. The numbers of neurons in the hidden layer are decided via trial and error. In this process, the point to take into consideration is to avoid a possible loss in ability of generalization of the feed forward neural network. The inputs of FFANN consist of membership values and these membership values are obtained by applying operation of union to the vector of membership values of observations of each lagged time series. For example, we consider three order fuzzy time series forecasting model. Let the number of fuzzy sets be three. The membership values are given in Table 1.
|
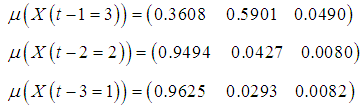 and then;
and then;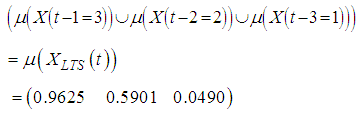 The architecture of the network is shown in Figure 2 with 3 fuzzy sets and 2 neurons in the hidden layer. In Figure 2,
The architecture of the network is shown in Figure 2 with 3 fuzzy sets and 2 neurons in the hidden layer. In Figure 2, 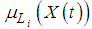 denotes the membership degree of belonging to ith fuzzy set of related observation of time series X(t). Then, the target values of FFANN are every membership degrees of belonging to c fuzzy sets of the observation of time series at t while the inputs of the networks are every membership degrees of belonging to c fuzzy sets of the observation of lagged time series at t
denotes the membership degree of belonging to ith fuzzy set of related observation of time series X(t). Then, the target values of FFANN are every membership degrees of belonging to c fuzzy sets of the observation of time series at t while the inputs of the networks are every membership degrees of belonging to c fuzzy sets of the observation of lagged time series at t 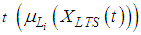 .
.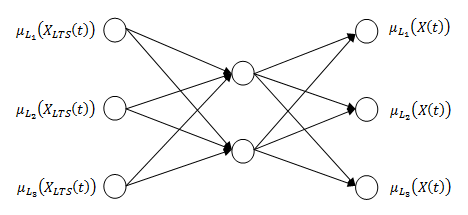 | Figure 2. The architecture of the feed forward network with 3 fuzzy sets |
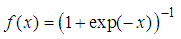 | (8) |
|
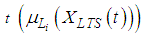 associated with the centers of the fuzzy sets
associated with the centers of the fuzzy sets 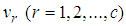 which are defined by the method of FCM clustering are obtained. Then, these membership degrees are given as input of FFANN and the output is generated. These outputs are actually the membership degrees for the fuzzy forecasting value of the observation at t. It should be here noted that the sum of the degrees of membership is not equal to 1, to the contrary FCM method. In defuzzification stage, the degrees of memberships of the fuzzy forecast are put in Equation (9) given below and are transformed into weights. And finally, the defuzzified forecast of the observation at t is calculated as in Equation (10).
which are defined by the method of FCM clustering are obtained. Then, these membership degrees are given as input of FFANN and the output is generated. These outputs are actually the membership degrees for the fuzzy forecasting value of the observation at t. It should be here noted that the sum of the degrees of membership is not equal to 1, to the contrary FCM method. In defuzzification stage, the degrees of memberships of the fuzzy forecast are put in Equation (9) given below and are transformed into weights. And finally, the defuzzified forecast of the observation at t is calculated as in Equation (10).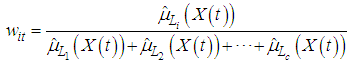 | (9) |
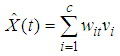 | (10) |
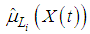 , i=1,2,…,c denotes the membership degrees for the fuzzy forecasting value of the observation at t obtained from the output of FFANN,
, i=1,2,…,c denotes the membership degrees for the fuzzy forecasting value of the observation at t obtained from the output of FFANN, 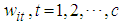 are weights used for defuzzifying forecasts.Referring back to Table 1, consider that we have got the output of ANN for third observation (t=4) like 0.87, 0.23, 0.02. In this case, we obtained
are weights used for defuzzifying forecasts.Referring back to Table 1, consider that we have got the output of ANN for third observation (t=4) like 0.87, 0.23, 0.02. In this case, we obtained 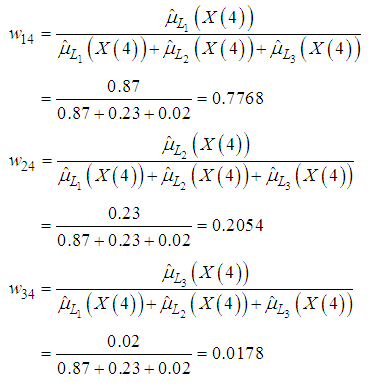
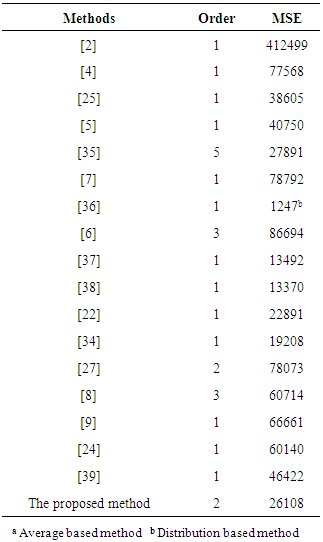
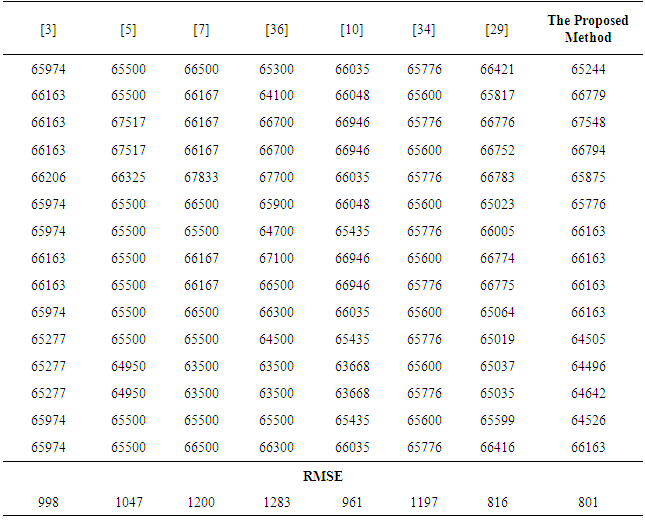
4. Applications
- In order to evaluate the performance of the proposed method, three different data sets which were used in previous studies were analyzed with both the proposed method and some other methods in the literature. Besides, the all of the obtained results were evaluated as comparatively over the training sets and the test sets, together. In the comparison, mean square error (MSE) and root mean square error (RMSE) given in (11) are being calculated.
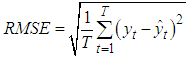 | (11) |
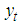 and
and 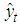 , T represent crisp time series, defuzzified forecasts, and the number of forecasts, respectively. The algorithm of the proposed method is coded in MATLAB version 7.9.
, T represent crisp time series, defuzzified forecasts, and the number of forecasts, respectively. The algorithm of the proposed method is coded in MATLAB version 7.9.4.1. The Enrollment Data of University of Alabama
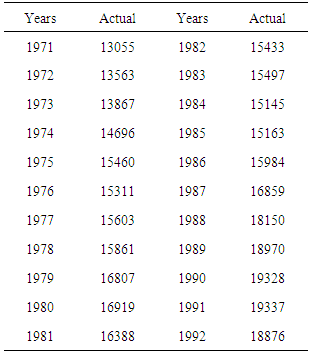
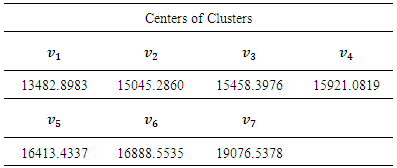
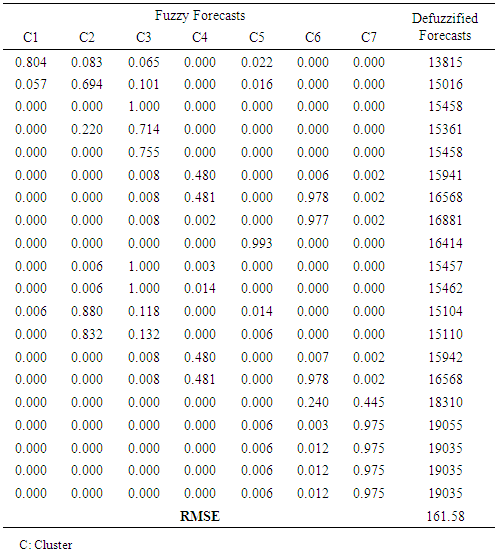
- First of all we aim to evaluate the forecasting performance of the proposed method over the training data set. For this purpose, the proposed method was applied to the enrollment data of University of Alabama between the years 1971 and 1992. The enrollment data is given in Table 3.
|
|
|
|
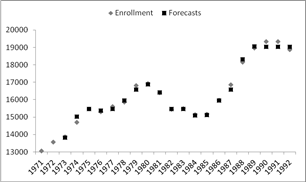 | Figure 3. The graph of forecasts and observations |
|
4.2. Index 100 in Stock Market of Istanbul
- In order to evaluate the performance of the proposed method, the other fuzzy time series data is index 100 in stock market of Istanbul (BIST). Data set includes observations between 01.10.2010 – 23.12.2010. The graph of the data set is shown in Figure 4. The last fifteen observations of data set are used for test set.
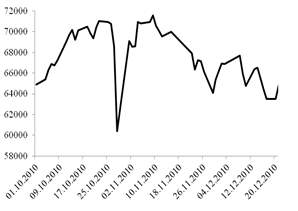 | Figure 4. The data set of BIST |
|
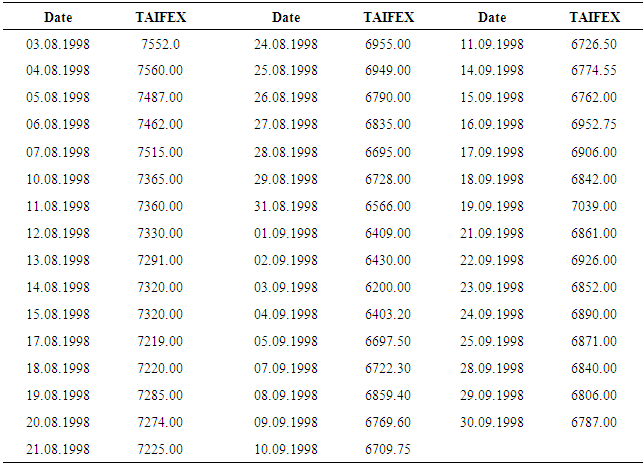
4.3. Taiwan Futures Exchange (TAIFEX) Data
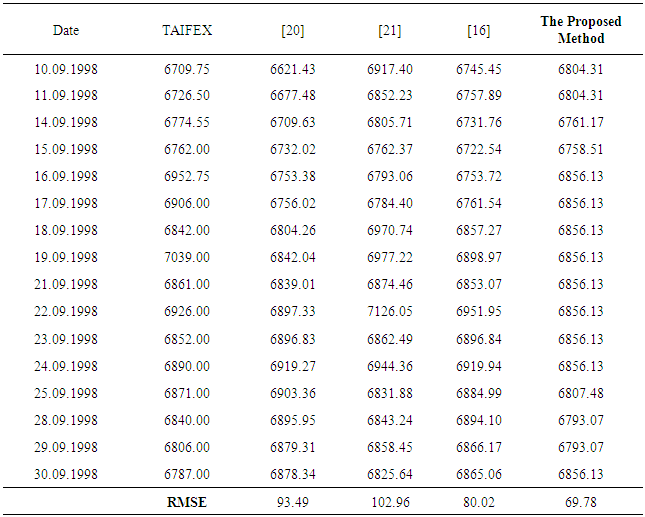
- Finally, the proposed forecasting approach is applied to TAIFEX data presented in Table 9. The time series has 47 daily observations between 03.08.1998 and 30.09.1998. The last 16 observations between 10.09.1998 and 30.09.1998 are used for test set.
|
|
5. Discussion and Conclusions
- Although fuzzy time series approaches provide some advantages, they also have some disadvantages. Some of them require subjective decisions especially in fuzzification stage and ignore the membership values. These drawbacks directly affect the forecasting performance. In this study, a new high order fuzzy time series forecasting model is proposed to deal with these problems. The proposed model determines the membership values systematically by using FCM technique in the fuzzification stage. These membership values were used in the stage of determination of fuzzy relations and so better forecasting results can be obtained by using more information.Moreover, in the proposed method, using the operation of union overcome the problem that is too much input for artificial neural network models. In the implementation, the proposed method has been applied to various time series and the forecasting performance has been evaluated for both training and test sets. The obtained results show that the proposed method has superior forecasting performance besides its all advantages.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML