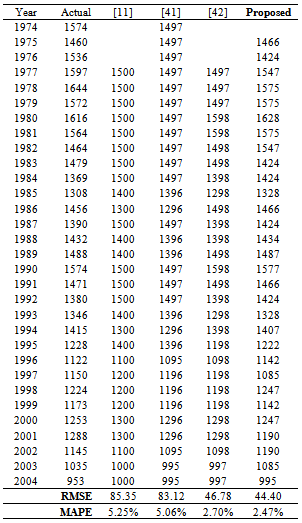-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Intelligent Systems
p-ISSN: 2165-8978 e-ISSN: 2165-8994
2013; 3(2): 75-82
doi:10.5923/j.ajis.20130302.04
A Fuzzy Time Series Analysis Approach by Using Differential Evolution Algorithm Based on the Number of Recurrences of Fuzzy Relations
Eren Bas1, Vedide Rezan Uslu2, Ufuk Yolcu1, Erol Egrioglu2
1Department of Statistics, Giresun University, Giresun, 28000, Turkey
2Department of Statistics, University of OndokuzMayis, Samsun, 55139, Turkey
Correspondence to: Erol Egrioglu, Department of Statistics, University of OndokuzMayis, Samsun, 55139, Turkey.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Fuzzy time series approaches are used when the observations of traditional time series approaches contain uncertainty. Besides, fuzzy time series approaches do not need the assumptions valid for traditional time series approaches. Generally, fuzzy time series methods consist of three stages. These are fuzzification, determination of fuzzy relations and defuzzification stages, respectively. All these stages of fuzzy time series are very important on the forecasting performance of the model. There are many studies that contribute for each stage in the literature. In this study, we contributed the fuzzification and defuzzification stages. In fuzzification stage, we used Differential Evaluation Algorithm to avoid subjective judgments for determining the interval lengths and also as known; the forecasting performance may be improved if the fuzzy relations must be occurred, properly. From this point of view, we take into account the recurrence numbers of fuzzy relations in defuzzification stage. Then, our proposed method has been applied to the real data sets which are often used in other studies in literature. The results are compared to the ones obtained from other techniques. Thus it is concluded that the results present superior forecasts performance.
Keywords: Fuzzy Time Series, Recurrence Numbers, Forecasting, Differential Evaluation Algorithm.
Cite this paper: Eren Bas, Vedide Rezan Uslu, Ufuk Yolcu, Erol Egrioglu, A Fuzzy Time Series Analysis Approach by Using Differential Evolution Algorithm Based on the Number of Recurrences of Fuzzy Relations, American Journal of Intelligent Systems, Vol. 3 No. 2, 2013, pp. 75-82. doi: 10.5923/j.ajis.20130302.04.
Article Outline
1. Introduction
- Fuzzy time series procedures do not require the assumptions such as the large sample and that the model is true. Recent studies are about fuzzy time series procedures since they do not require the strict assumptions and generally provide remarkable forecasting performances. The fuzzy set was firstly introduced by Zadeh[1] and this concept has found many application areas since then. Fuzzy time series were introduced firstly in the studies of[2, 3, 4]. These proposed fuzzy time series techniques in literature generally consist of the three stages; these are fuzzification, determining of fuzzy relations and defuzzification.In the literature, the decomposition of universe of discourse was mostly used in the fuzzification stage and intervals of it was determined arbitrarily the studies of[2, 3, 4, 5,6]. In addition, Huarng[7] has put forward the importance of the interval length on the forecasting performance and proposed two new techniques based on the mean and the distribution in order to find intervals. Egrioglu et al.[8, 9] have suggested forming the problem of finding intervals as an optimization problem.Chen and Chung[10] and Lee et al.[11] used genetic algorithm to find the interval lengths, and also Fu et al.[12], Huang et al.[13], Kuo et al.[14, 15], Davari et al.[16], Park et al.[17] and Hsu et al.[18] used the particle swarm optimization. Besides these studies, Cheng et al.[19] and Li et al.[20] used fuzzy C-means clustering method in their studies and also Egrioglu et al.[21] used Gustafson-Kessel fuzzy clustering method in this stage.In the stageof determining of fuzzy relations, while Song and Chissom[2, 3, 4] used matrix operations, Chen[5] and some others were used the fuzzy logic relations group table and also artificial neural networks were used in the studies of[7, 22, 23, 24, 25, 26] for determining the fuzzy relations. The other studies in this stage were proposed in the studies of[23, 27, 28, 29].In defuzzification stage, studies in the literature mostly used the centroid method. Chen[5], Huarng[7]. Cheng et al.[30], Aladag et al.[28] preferred to use adaptive expectation method in the defuzzification process.The determining of the fuzzy relations is very important for the model structure. Besides, the forecasting performance may be improved if the fuzzy relations defined well. From this point of view, we used Differential Evaluation Algorithm (DEA) in fuzzification stage to avoid subjective decisions and also we aimed to obtain more realistic forecasts by using fuzzy relations recurrence numbers. Because, using recurrence numbers of fuzzy relations is important as well as fuzzy relations occur or not.In this study, a fuzzy time series approach that uses DEA in fuzzification stage and takes into account the recurrence numbers of fuzzy relations was proposed and also the proposed method was supported by the applications and it is superior forecasting performance was shown.The rest part of the paper can be outlined as below: The fundamental definitions of fuzzy time series has been given in Section 2. Short information about DEAhas been given in Section 3. In Section 4, the proposed method has been introduced. In Section 5, the results from the application of the proposed method to three real life data sets have presented. In section 6, discussionshave been presented and finally in section 7, conclusions havebeen presented.
2. Fuzzy Time Series
- The definition of fuzzy time series was firstly introduced by Song and Chissom[2, 3, 4]. In contrast to conventional time series methods, various theoretical assumptions do not need to be checked in fuzzy time series approaches. The most important advantage of the fuzzy time series approaches is to be able to work with a very small set of data. Let U be the universe of discourse,where
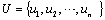 . A fuzzy set
. A fuzzy set 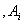 of U can be defined as,
of U can be defined as,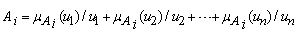 | (1) |
 is the membership function of the fuzzy set
is the membership function of the fuzzy set  and
and  .In addition to,
.In addition to, 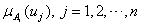 denotes is a generic element of fuzzy set
denotes is a generic element of fuzzy set is the degree of belongingness of
is the degree of belongingness of 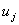 to
to .Definition 1 Let
.Definition 1 Let 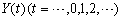 , a subset of real numbers, be the universe of discourse by which fuzzy sets
, a subset of real numbers, be the universe of discourse by which fuzzy sets 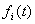 are defined. If
are defined. If  is a collection of
is a collection of 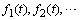 then
then  is called a fuzzy time series defined on Y(t).Definition 2 Fuzzy time series relationships assume that is caused only by
is called a fuzzy time series defined on Y(t).Definition 2 Fuzzy time series relationships assume that is caused only by  then the relationship can be expressed as:
then the relationship can be expressed as: 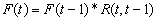 , which is the fuzzy relationship between
, which is the fuzzy relationship between  and
and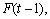 where * represents as an operator. To sum up, let
where * represents as an operator. To sum up, let 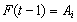 and
and  . The fuzzy logical relationship between
. The fuzzy logical relationship between 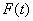 and
and 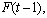 can be denoted as
can be denoted as 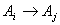 where
where 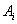 (current state) refers to the left-hand side and
(current state) refers to the left-hand side and 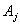 (next state) refers to the right-hand side of the fuzzy logical relationship. Furthermore, these fuzzy logical relationships can be grouped to establish different fuzzy relationship.
(next state) refers to the right-hand side of the fuzzy logical relationship. Furthermore, these fuzzy logical relationships can be grouped to establish different fuzzy relationship.3. Differential Evaluation Algorithm
- DEA was proposed by Price and Storn[31]. DEA is a heuristic algorithm based on the population. It has some operators such as mutation and crossover operations. These operators are used to create new generations. At the end of the process, candidate solutions are found by using some mathematical operations and these solutions are compared with the current solutions in the population. The best solution is transferred to the new generation according to the evaluation function and the best chromosome is taken as the optimal solution. DEA and its operators discussed in more detail in the section of proposed method and also those who want more information can look the study of Price and Storn[31].
4. Proposed Method
- As it is well known that all stages of the fuzzy time series approaches influences very much intensively on the forecasting performance of the applied model and researchers have used different techniques to make a contribution to each stages. In recent years, artificial intelligence algorithms have been used in fuzzification stage by the researchers and also the researchers have generally preferred to use the centroid method in the last stage so far and also the stage of determining of the fuzzy relations is very important as well as the other stages of fuzzy time series approaches. Besides, the forecasting performance may be improved if the fuzzy relations defined well. From this point of view; we have noticed that none of them have considered how many times a fuzzy relation has occurred.To overcome this problem, the weights can be given for each fuzzy relation according to their recurrences. Then, these weights can be used in the defuzzification stage. Because using recurrence numbers of fuzzy relations is important as well as fuzzy relations occur or not and the forecasting performance may be improved with the help of using these recurrence numbers In this study, a fuzzy time series method that uses DEA in fuzzification stage and takes into consideration of recurrence numbers of fuzzy relations in defuzzification stage to obtain more realistic forecasts has been proposed.The main advantages of proposed method are as follows:• The interval lengths are determined by avoiding subjective decisions because of using DEA.• A more flexible solution process is provided by obtaining fix interval length instead of constant length interval.• The most basic element in the structure of the model is fuzzy relations. To obtain forecasts as well as the fuzzy relations, using their recurrence numbers cause to obtain more realistic forecasts.• The search space has been differentiated by using DEA and new generations are obtained.Briefly, we can summarize our proposed method as below.Algorithm.Step 1
 and
and 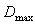 are the minimum and maximum values of time series, respectively and the universe of discourse is defined in Equation 2.
are the minimum and maximum values of time series, respectively and the universe of discourse is defined in Equation 2. | (2) |
 and
and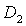 are the numbers determined arbitrarily.If genes are shown with
are the numbers determined arbitrarily.If genes are shown with 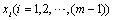 a chromosome structure of DEA can be shown as follows.
a chromosome structure of DEA can be shown as follows.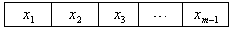 | Figure 1. A chromosome structure of DEA |
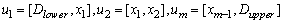 | (3) |
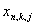 is to show the n. gene of k. chromosome of j. generation
is to show the n. gene of k. chromosome of j. generation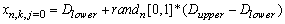 | (4) |
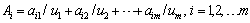 | (5) |
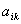 is the membership degrees and it is shown in equation 6.
is the membership degrees and it is shown in equation 6. | (6) |
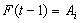 and
and 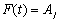 for any time t this fuzzy logic relation is represented by
for any time t this fuzzy logic relation is represented by 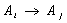 . In the whole series if we get the relation
. In the whole series if we get the relation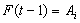 and
and 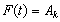 for any time t then we express the fuzzy logic relation as
for any time t then we express the fuzzy logic relation as 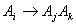 . Also we save the number of how many times the fuzzy logic relation such as
. Also we save the number of how many times the fuzzy logic relation such as 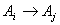 is occurred, into the weights
is occurred, into the weights  . Step 3.3 Obtain the fuzzy forecasts. The fuzzy forecasts are obtained with respect to the fuzzy logic relation table. If
. Step 3.3 Obtain the fuzzy forecasts. The fuzzy forecasts are obtained with respect to the fuzzy logic relation table. If 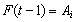 and there is a relation such as
and there is a relation such as 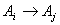 in the fuzzy logic relation table then the fuzzy forecast will be
in the fuzzy logic relation table then the fuzzy forecast will be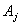 . If
. If 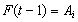 and there is a relation such as
and there is a relation such as 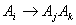 in the fuzzy logic relation table then the fuzzy forecast will be
in the fuzzy logic relation table then the fuzzy forecast will be 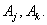 If
If 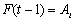 and
and 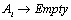 in the fuzzy logic relation table then the fuzzy forecast will be
in the fuzzy logic relation table then the fuzzy forecast will be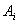 . Step 3.4 Defuzzify the fuzzy forecasts. The weights
. Step 3.4 Defuzzify the fuzzy forecasts. The weights 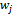 obtained from the fuzzy logic relation table are used in the defuzzification stage. For example; If
obtained from the fuzzy logic relation table are used in the defuzzification stage. For example; If 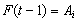 and there exists the relation
and there exists the relation  in the table then the defuzzified forecast will be
in the table then the defuzzified forecast will be  which is the midpoint of
which is the midpoint of 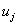 which is the subinterval of the fuzzy set
which is the subinterval of the fuzzy set  with the largest membership degree. That is, we don’t regard how many times that relation is repeated in the table. If
with the largest membership degree. That is, we don’t regard how many times that relation is repeated in the table. If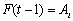 and there exists the relation
and there exists the relation  and
and  is the number of how many times the relation
is the number of how many times the relation 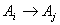 is repeated in the whole time series and
is repeated in the whole time series and 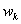 is the number of how many times the relation
is the number of how many times the relation 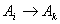 is repeated then the defuzzified forecast is calculated as below.
is repeated then the defuzzified forecast is calculated as below.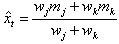 | (7) |
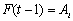 and there exists the relation
and there exists the relation 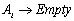 in the fuzzy logic relation table then the defuzzified forecast will be
in the fuzzy logic relation table then the defuzzified forecast will be  which is the midpoint of the subinterval
which is the midpoint of the subinterval  which is the fuzzy set
which is the fuzzy set 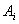 with the largest membership degree. Step 3.5 Let
with the largest membership degree. Step 3.5 Let 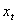 be the original time series and
be the original time series and 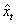 be its defuzzified forecasts with the nobservations. RMSE is calculated by the equation 8.
be its defuzzified forecasts with the nobservations. RMSE is calculated by the equation 8.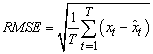 | (8) |
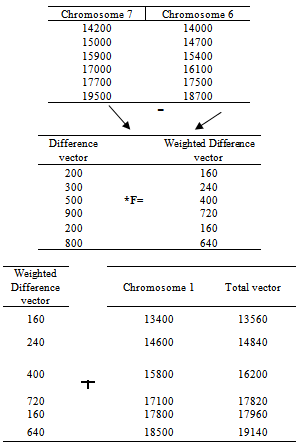 | Figure 2. An example of mutation operation |
|
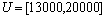 as given in Table 1. and assume that the Chromosome 2 is the chromosome to be mutated and Chromosome 6, Chromosome 7, Chromosome 1 are the chromosomes selected randomly except Chromosome 2. Step 4.2 The application of Crossover.To apply Crossover operation, the total vector obtained from at the end of the mutation operation is compared with current chromosome and nominee chromosome is obtained.While nominee chromosome is obtained, each gene of total vector and current chromosome is evaluated one by one.First at all, a crossover rate (cor) is determined. Then, a random number is generated between 0 and 1 with the help of uniform distribution.If this random number is smaller than the crossover rate, the gene is taken from total vector. If it is not, the gene is taken from currentchromosome and nominee chromosome is generated and the fitness value of nominee chromosome is calculated.Then, let’s determine the (cor) rate. For example let’s take it 0.10 than generate random numbers for each gene, respectively. (0.01, 0.08, 0.15, 0.20, 0.16) and obtain the nominee chromosome. An example of crossover has been given in Figure 3.
as given in Table 1. and assume that the Chromosome 2 is the chromosome to be mutated and Chromosome 6, Chromosome 7, Chromosome 1 are the chromosomes selected randomly except Chromosome 2. Step 4.2 The application of Crossover.To apply Crossover operation, the total vector obtained from at the end of the mutation operation is compared with current chromosome and nominee chromosome is obtained.While nominee chromosome is obtained, each gene of total vector and current chromosome is evaluated one by one.First at all, a crossover rate (cor) is determined. Then, a random number is generated between 0 and 1 with the help of uniform distribution.If this random number is smaller than the crossover rate, the gene is taken from total vector. If it is not, the gene is taken from currentchromosome and nominee chromosome is generated and the fitness value of nominee chromosome is calculated.Then, let’s determine the (cor) rate. For example let’s take it 0.10 than generate random numbers for each gene, respectively. (0.01, 0.08, 0.15, 0.20, 0.16) and obtain the nominee chromosome. An example of crossover has been given in Figure 3.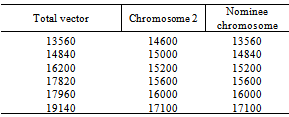 | Figure 3. An example of Crossover |
|
5. Application
- In order to show the performance of the proposed method this is applied to three different time series data. The results are compared with the results from the methods which are already in fuzzy time series literature with regards to RMSE and Mean Absolute Percent Error (MAPE) criteria.
 | (9) |
5.1. Enrollment Data
- The performance of proposed method is evaluated separately for both test and training sets for enrollment data between the years 1971 and 1992. Firstly all data is used for training set like almost all studies in the literature and then the last three observations of enrollment data is taken as test set and it is compared with the other studies in the literature. It is clearly seen that our proposed method has superior forecasting performance. As a first experiment, the proposed method is solved for training data. We conclude that the best result is obtained in the case where m=19, cn=80, cor=0.9. Table 3 presents the all results, which include forecasts and the RMSE and MAPEvalues, obtained from the proposed method and the other methods proposed in literature, comparatively. These results from both are belonging to the best case.Additionally, a comparative presentation of enrollments’ forecasts in terms of RMSE values for some other methods is given Table 4.As a second experiment, the proposed method is solved for test data. We conclude that the best result is obtained in the case where m=16, cn=60, cor=0.3. Table 5 presents the all results, which include RMSE values, obtained from the proposed method and the other methods proposed in literature, comparatively.
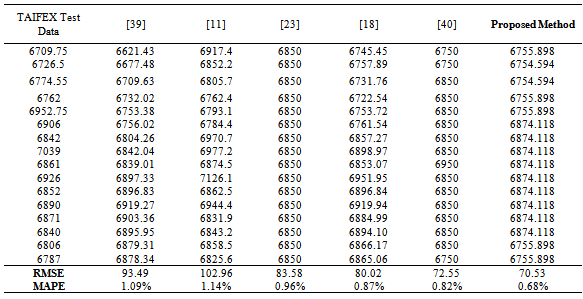
5.2. Taifex Data
- In the second case, the proposed method was applied to TAIFEX data whose observations are between 03.08.1998 and 30.09.1998. The last 16 observations are used for test set, respectively. We conclude that the best result is obtained in the case where m=12, cn=70, cor=0.9. Table 6 presents the all results, which include forecasts and the RMSE and MAPE values, obtained from the proposed method and the other methods proposed in literature, comparatively. These results from both are belonging to the best case.
|
|
|
|
5.3. Car Road Accident in Belgium Data
- In the third case, the proposed method was implemented on the time series data of ‘killed in car road accident in Belgium’. We conclude that the best result is obtained in the case where m=20, cn=80, cor=0.2. Table 7 presents the all results, which include forecasts and the RMSE and MAPE values, obtained from the proposed method and the other methods proposed in literature, comparatively. These results from both are belonging to the best case.As seen in Table 7, the method we propose gives the best result with respect to the forecasting performance.
6. Discussions
- Using recurrence numbers of fuzzy relations is important as well as fuzzy relations occur or not.And also the forecasting performance may be improved with the help of using these recurrence numbers of fuzzy relations Besides, more reliable results may be obtained by giving weights as the number of repetitions of recurrent fuzzy relations. Besides, the contribution of fuzzy relations recurrent more is more than the fuzzy relations recurrent less. We also considered this contribution and gave more weights to the fuzzy relations recurrent more.
|
7. Conclusions
- Fuzzy time series forecasting methods have attracted much attention in recent years. Different approaches have been proposed for the each stage of fuzzy time series approaches. The stage of determining of fuzzy relation is very important for fuzzy time series approachesbecause it affects defuzzification stage. Revealing the effects of fuzzy relations, properly may improve the forecasting performance. From this point of view, we used DEA in fuzzification stage to avoid subjective decisions and also we consider the recurrence numbers of the repeated relations in fuzzy logic relation table which is necessary in the defuzzification stage in this study. By using recurrence numbers of fuzzy relations the forecasting performance was improved. The proposed method was supported by the real data sets analysis and its superior forecasting performance was shown.We expect that in future studies researchers can concentrate on a different optimization technique for finding the weights used in the defuzzification stage and may use different artificial intelligence techniques in fuzzification stage.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML