-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Intelligent Systems
p-ISSN: 2165-8978 e-ISSN: 2165-8994
2013; 3(2): 57-70
doi:10.5923/j.ajis.20130302.02
Multiclass Adaboost based on an Ensemble of Binary AdaBoosts
1Department of Computer Engineering, School of Technology and Business Studies, Dalarna University, Rödavägen 3, Borlänge, 78188, Sweden
2University of Central Florida, Orlando, 4000 central Florida blvd, Orlando FL 32816, USA
Correspondence to: Hasan Fleyeh, Department of Computer Engineering, School of Technology and Business Studies, Dalarna University, Rödavägen 3, Borlänge, 78188, Sweden.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
This paper presents a multi-class AdaBoost based on incorporating an ensemble of binary AdaBoosts which is organized as Binary Decision Tree (BDT). It is proved that binary AdaBoost is extremely successful in producing accurate classification but it does not perform very well for multi-class problems. To avoid this performance degradation, the multi-class problem is divided into a number of binary problems and binaryAdaBoost classifiers are invoked to solve these classification problems. This approach is tested with a dataset consisting of 6500 binary images of traffic signs. Haar-like features of these images are computed and the multi-class AdaBoost classifier is invoked to classify them. A classification rate of 96.7% and 95.7% is achieved for the traffic sign boarders and pictograms, respectively. The proposed approach is also evaluated using a number of standard datasets such as Iris, Wine, Yeast, etc. The performance of the proposed BDT classifier is quite high as compared with the state of the art and it converges very fast to a solution which indicates it as a reliableclassifier.
Keywords: Multiclass AdaBoost, Binary Decision Tree, Classification
Cite this paper: Hasan Fleyeh, Erfan Davami, Multiclass Adaboost based on an Ensemble of Binary AdaBoosts, American Journal of Intelligent Systems, Vol. 3 No. 2, 2013, pp. 57-70. doi: 10.5923/j.ajis.20130302.02.
Article Outline
1. Introduction
- Boosting[1] is a machine learning meta-algorithm to perform supervised learning which combines several weak learners to create a strong learner. A weak learner is a classifier which can classify samples with success rates a slightly more than randomly guessing the sample’s class. A strong learner is a classifier that can classify data with rather high rates which meansbetter rates than what can be achieved by weak learners. It is based on a very basic principle “Pay more attention to the misclassified samples and next time try to classify them correctly”. The original boosting algorithms were proposed by Schapire[2] and Freund[3]. The proposed algorithmscould not take full advantage of the weak learners because they were not adaptive.Boosting is not limited by algorithm constraints such as the number of training samples, the dimension of each sample, and the number of training rounds. After each round of learning, the weights (importance) of all the samples are updated based on the classification error of the weak learner of that round. The samples which are misclassified gain weight and samples which are correctly classified lose weight.AdaBoost[4] which is a binary boosting algorithm and perhaps the most significant one represents the basic milestone of many otherclassification algorithms such as Boost by Majority[3], LPBoost[5], TotalBoost[6],BrownBoost[7], MadaBoost[8], and LogitBoost[9]. This boosting algorithm divides the dataset into two classes. Extending Adaboost directly to more than two classes was avoided because it does not perform as good as its binary companion [10].The extension of binary classification to multi-class one is not straightforward. The problem can be tackled by using an ensemble of classifiers which decomposes the multi-class problem into a number of binary-class problems and tackle each oneindividually. Among the techniques invoked to solve such kinds of problems is the One-against-All in which N-class problem (N>2) can be solved by N binary classifiers. In the training phase, the ith class is labelled as positive in the ith classifier and the rest of the classes as negative. While in the recognition phase, the test example is presented to all classifiers and is labelled according to the maximum output among the N classifiers. The main drawback of this approach is the high training complexity due the large training number of samples. The other famous approach is the One - against-One which consists of N(N-1)/2 classifiers. Each classifier is trained using the samples of one class as positive and the samples of the other class as negative. Voting by majority approach is adopted to decide the winning classifier. The disadvantage of this approach is that the test sample should be presented to a large number of classifiers which results slow testing process[11].In this paper, Binary Decision Tree (BDT) is proposed as a strategy to extend the binary AdaBoost into a multi-class classifier which incorporates an ensemble of binary classifiers in each node of the BDT. It takes advantage of the high classification accuracy of the AdaBoost and the efficient computation of the BDT. The approach requires (N-1) binary Adaboosts to be trained to classify N classes but it only requires log2 (N) classifiers to recognize a pattern.The reminder of the paper is organised as follows. In Section 2, the relevant work is presented while the AdaBoost is introduced in Section 3. A full description of the proposed approach of multi-class AdaBoost is given in Section 4.The experiments and results based on the proposed method are given in Section 5, and in Section 6, the conclusions are presented.
2. Related Work
- The original Boosting methods were developed by Schapire and Freund[2; 3]. AdaBoost was the result of further improvementson the former boosting algorithms[4]. Adaptability is achieved in the way that current weak classifiers would be able to focus more on the data which is misclassified by the previous weak classifiers.Freund and Schapire[10][4] developed the AdaBoost.M1 which is a viable straightforward generalization of the binary AdaBoost. It extends directly the two-class AdaBoost algorithm to the multi-class algorithm with multi-class classifiers as weak learners. It needs a performance of all weak classifiers to be greater than 0.5.Freund and Schapire[10]implemented the AdaBoost.M2 with C4.5 and random nearest neighbor as weak learner. Holger and Yoshua[12] and Opitz and Maclin[13]implemented this classifier with neural networks as weak learners. They concluded that the first few classifiers were responsible for the performance improvements and theclassifier could achieve perfect performance with fewer classifiers. This classifier is also called AdaBoost.MR (AdaBoost with Ranking Loss)[10; 14].AdaBoost.MH (AdaBoost with Multi-class Hamming Loss) which was developed by Schapire and Singer[14]is a multi-class algorithm with Hamming loss, which can be regarded as the average exponential loss on L binary classification problems.Allwein et al.[15] developed a general approach to transform the multi-class problem into several binary problems. It is based on the concept of Error-Correcting Output Coding (ECOC) which employs in its simple form the Hamming coding for this transformation. Jin et al.[16] proposed AdaBoost framework which uses neural networks as weak classifiers. The neural network directly yields a multi-class weak learner. It is called AdaBoost.HM (AdaBoost with Hypothesis Margin) in which the hypothesis margin was originated from the LVQ. The classifier has the ability to tighten the upper bound of the training error which yields better performance. Indraneel and Schapire[17] created a broad and general framework, within which they make precise and identify the optimal requirements on the weak-classifier, as well as design the most effective, in a certain sense, boosting algorithms that assume such requirements.Zhu et al.[18] proposed a multi-class algorithm which extends the binary AdaBoost to multi-class Adaboost which is called SAMME (Stagewise Additive Modeling using Multi-class Exponential loss function). The algorithm adaptively combines the weak learners as in the case of binary AdaBoost by fitting a forward stagewise additive model for multi-class problem. The proposed classifier performs better than AdaBoost.MH.Benbouzid et al.[19] created a full multi-purpose multi-class multi-label boosting package which implemented in C++ and based on AdaBoost.MH. The package allows other cascade classifiers and filterboost. The user can choose different base learners as well as the strong classifiers.
3. AdaBoost
- AdaBoost is a classification algorithm which calls a given weak learner algorithm repeatedly in a series of rounds. A weak learneris a learning algorithm which performs just slightly better than random guessing and findsa separation boundary between two classes (positive and negative). AdaBoost combines a number of weak learners to form a strong learner in order to achieve better separation between classes.The strong learner is a weighted majority vote of the weak learners. Figure 1 demonstrates a simple binary classification case in which a weak learner is invoked to give a rough separation of the two classes, and a strong learner is formed by combining the weak learners of each classification round. Such strong learner would accomplish the final classification task.Let X be a finite training set which is denoted by:
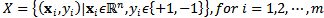 | (1) |
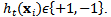
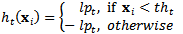 | (2) |
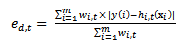 | (3) |
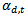 , which is a positive number in the range[0, ∞][5], is given by
, which is a positive number in the range[0, ∞][5], is given by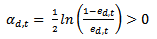 | (4) |
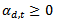 if
if 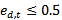 and that
and that 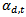 becomes larger when
becomes larger when 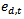 becomes smaller. In each round t, there is one weak learner in each dimension d which is now described by four parameters[thd,t, lpd,t, dt, αd,t]. The best weak learner among all weak learners in all dimensions in round t is the one which generate the least classification error et. It is given by:
becomes smaller. In each round t, there is one weak learner in each dimension d which is now described by four parameters[thd,t, lpd,t, dt, αd,t]. The best weak learner among all weak learners in all dimensions in round t is the one which generate the least classification error et. It is given by: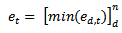 | (5) |
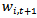 of sample xi in round t+1 according to the weight
of sample xi in round t+1 according to the weight 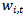 in round t by the following equation:
in round t by the following equation: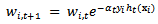 | (6) |
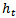 , and decreases when the weak learner correctly classifies the examples. By this way AdaBoost gives more attention to the wrongly classified samples.Finally the strong classifier is updated by the following equation:
, and decreases when the weak learner correctly classifies the examples. By this way AdaBoost gives more attention to the wrongly classified samples.Finally the strong classifier is updated by the following equation: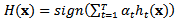 | (7) |
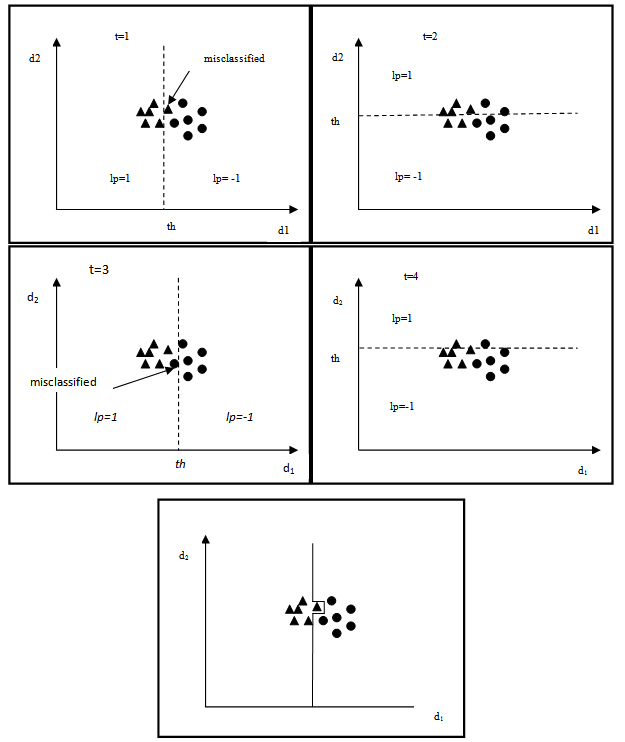 | Figure 1. A weak learners (Top) versus a strong learner (Bottom) |
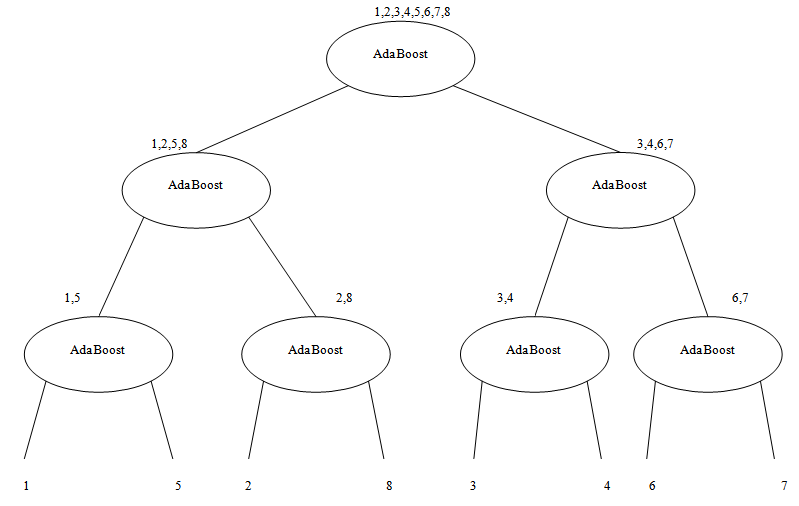 | Figure 2. Multi-class AdaBoost designed by Binary Decision Tree |
4. The Proposed Approach
- AdaBoost in its original form was designed for binary classification. It has been proved that this classifier is extremely successful in producing accurate classification when applied to two-class classification problems[20]. AdaBoost was also proposed to be used as multi-class classifier by Freund and Schapire[4]. However, it does not perform as good as its binary companion. As described in Section 3, in order for the misclassified training samples to be boosted,the error
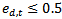 and that
and that 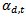 gets larger when
gets larger when 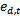 get smaller. When dealing with binary problems, this constraint is solved as it is almost the same as random guessing. However, when the number of classes increases, it becomes very hard to achieve this constraint. In other words, when the error of the weak classifier becomes more than 0.5,
get smaller. When dealing with binary problems, this constraint is solved as it is almost the same as random guessing. However, when the number of classes increases, it becomes very hard to achieve this constraint. In other words, when the error of the weak classifier becomes more than 0.5, 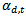 gets smaller. This means that the weights of the training samples will be updated in the wrong direction. Hence AdaBoost fails in achieving the multi-class classification task[10]. In is order to keep the very successful binary classifier as the core and achieve multi-class classification (N>2), it is necessary to divide this multi-class problem into a number of binary problems provided that this division should rely on classes’ properties and theircommon similarities.Binary Decision Tree decomposes N class problem into N-1 binary problems. The proposed algorithm takes advantage of the high classification accuracy achieved by the AdaBoost and the efficient architecture of the BDT architecture. It is based on recursively dividing the classes into two disjoint groups in each node of the BDT, as illustrated in Figure 2. In the root of the BDT, the classes are decomposed into two disjoint sets where classes with similar features are grouped in the same set. These two sets are further decomposed in each level of the BDT until the leaves are reached. The number of leaves in the tree is equivalent to the number of classes in the original set. Each node of this BDT contains anAdaBoostwhich is trained to decide to which of the two branches of the node the unknown sample will be assigned.Let N be the number of classes to be classified, and
gets smaller. This means that the weights of the training samples will be updated in the wrong direction. Hence AdaBoost fails in achieving the multi-class classification task[10]. In is order to keep the very successful binary classifier as the core and achieve multi-class classification (N>2), it is necessary to divide this multi-class problem into a number of binary problems provided that this division should rely on classes’ properties and theircommon similarities.Binary Decision Tree decomposes N class problem into N-1 binary problems. The proposed algorithm takes advantage of the high classification accuracy achieved by the AdaBoost and the efficient architecture of the BDT architecture. It is based on recursively dividing the classes into two disjoint groups in each node of the BDT, as illustrated in Figure 2. In the root of the BDT, the classes are decomposed into two disjoint sets where classes with similar features are grouped in the same set. These two sets are further decomposed in each level of the BDT until the leaves are reached. The number of leaves in the tree is equivalent to the number of classes in the original set. Each node of this BDT contains anAdaBoostwhich is trained to decide to which of the two branches of the node the unknown sample will be assigned.Let N be the number of classes to be classified, and 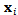 for
for 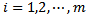 be a set of samples each of which is labelled by
be a set of samples each of which is labelled by 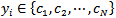 . Samples are divided into two disjoint groups
. Samples are divided into two disjoint groups 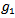 and
and 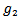 as described in the following steps:• Calculate the centre of class of each of the Ndifferent classes.• Assign the two classes with the largest Euclidian distance to the two disjoint groups
as described in the following steps:• Calculate the centre of class of each of the Ndifferent classes.• Assign the two classes with the largest Euclidian distance to the two disjoint groups 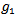 and
and 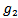 .• Repeat• Calculate the Euclidian distance of the remaining classes from both groups.• Assign the class with the smallest Euclidian distance from one of the two classes to that class.• Recalculate the centre of this set of classes.• Until all the remaining classes are assigned to either of the two groups.The pseudo code of the proposed algorithm is depicted in Algorithm 1. Note that this algorithm takes the training samples attributes and the corresponding classes as inputs and generates two lists of the classes to be disjoint. The algorithm generates BDT automatically during the training phase of the classification.
.• Repeat• Calculate the Euclidian distance of the remaining classes from both groups.• Assign the class with the smallest Euclidian distance from one of the two classes to that class.• Recalculate the centre of this set of classes.• Until all the remaining classes are assigned to either of the two groups.The pseudo code of the proposed algorithm is depicted in Algorithm 1. Note that this algorithm takes the training samples attributes and the corresponding classes as inputs and generates two lists of the classes to be disjoint. The algorithm generates BDT automatically during the training phase of the classification. 
5. Experiments and Discussions
- To evaluate the performance of the proposed multi-class AdaBoost, it is tested using two experiments. In the first experiment Haar-like features are computed for a set of traffic sign images and the multi-class AdaBoostis invoked to classify traffic sign in these images. While in the second experiment 8standard datasets such as Iris, Wine, Segment, etc.are employed to evaluate the performance of the classifier.
5.1. Classification of Traffic Signs
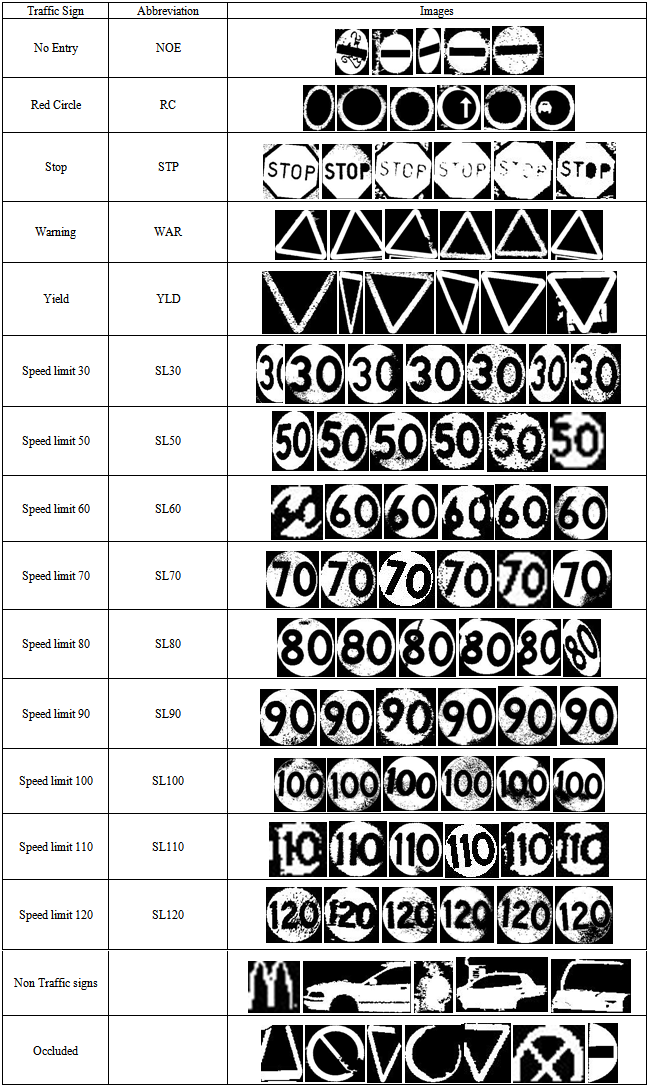
- The traffic sign dataset comprises 2996 images, among them there are 1070 images represent traffic sign shapes and 1926 images for speed limit traffic signs. All images invoked in this paper are available online[21]. Candidate objects are extracted and normalised as described in[22]. There are 6500 candidates extracted from these images which are grouped in three subsets representing the traffic sign borders (5 classes in 1060 binary images), speed limit pictograms (9 classes in 1810 images), and non-traffic sign objects such as vehicles, parts of buildings, billboards and other blobs (1 class in 3630 images).
|
 | Figure 3. Generating Haar-like features. (A): the way to compute Haar-like features for a candidate object. (B): different Haar matrices |
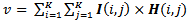 | (8) |
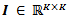 , K=36 pixels and
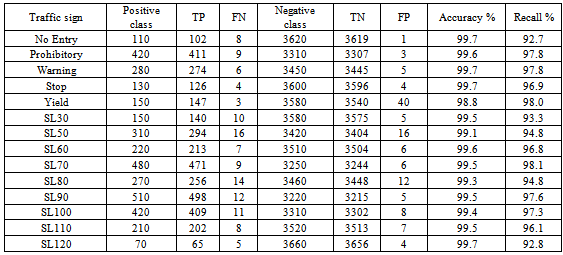
, K=36 pixels and 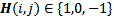 is the Haar matrix in which 1 means the blue areas in Figure 3A, -1 is the red area, and 0 means other pixels of the image which are not overlapped with the Haar matrix. The total number of Haar-like features exceeds 598 million becauseof the different Haar matrices employed in this experiment (Figure 3B) and the high number of images.Performance of the proposed multi-class AdaBoost, is evaluated by 10-fold cross validation. The classifier is trained and tested by the 598 million Haar-like features and the number of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) for each class are computed. Table 2 illustrates the average values of accuracy and recall[24] of the 10-fold cross validation computed per class, while Figure 4 depicts the results achieved by each of the 10 folds.The robustness of the proposed approach with respect to a situation in which traffic signs can be situated in different angles of rotation was also tested. The multi-class Adaboostis trained with Haar-like features of not-rotated signs and tested by images whichare rotated by different angles from -30o to +30o. Figure 5 depicts two samples of images invoked in the testing procedure.The classification rate achieved by the multi-class AdaBoost is computed for each rotation angle and plotted as shown in Figure 6. The classification rate has not been affected by the traffic sign’s angle of rotation which means that by employing the proposed method a system which is invariant to the angle of rotation can be achieved.Figure 7 depicts the ROC diagram of the multi-class AdaBoost for one of the final stages in the binary decision tree. In order to produce this ROC diagram, the strong classifier is trained with a training set consisting of Haar-like features of one certain class (positive class) and the Negative class images (negative class). The training is accomplished while the threshold of the weak learner is gradually increased from -∞ to +∞. The resulting classifier is then invoked to classify the test dataset of the positive class and the values of the false positive rates and the true positive rates are computed for each threshold value.
is the Haar matrix in which 1 means the blue areas in Figure 3A, -1 is the red area, and 0 means other pixels of the image which are not overlapped with the Haar matrix. The total number of Haar-like features exceeds 598 million becauseof the different Haar matrices employed in this experiment (Figure 3B) and the high number of images.Performance of the proposed multi-class AdaBoost, is evaluated by 10-fold cross validation. The classifier is trained and tested by the 598 million Haar-like features and the number of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) for each class are computed. Table 2 illustrates the average values of accuracy and recall[24] of the 10-fold cross validation computed per class, while Figure 4 depicts the results achieved by each of the 10 folds.The robustness of the proposed approach with respect to a situation in which traffic signs can be situated in different angles of rotation was also tested. The multi-class Adaboostis trained with Haar-like features of not-rotated signs and tested by images whichare rotated by different angles from -30o to +30o. Figure 5 depicts two samples of images invoked in the testing procedure.The classification rate achieved by the multi-class AdaBoost is computed for each rotation angle and plotted as shown in Figure 6. The classification rate has not been affected by the traffic sign’s angle of rotation which means that by employing the proposed method a system which is invariant to the angle of rotation can be achieved.Figure 7 depicts the ROC diagram of the multi-class AdaBoost for one of the final stages in the binary decision tree. In order to produce this ROC diagram, the strong classifier is trained with a training set consisting of Haar-like features of one certain class (positive class) and the Negative class images (negative class). The training is accomplished while the threshold of the weak learner is gradually increased from -∞ to +∞. The resulting classifier is then invoked to classify the test dataset of the positive class and the values of the false positive rates and the true positive rates are computed for each threshold value.
|
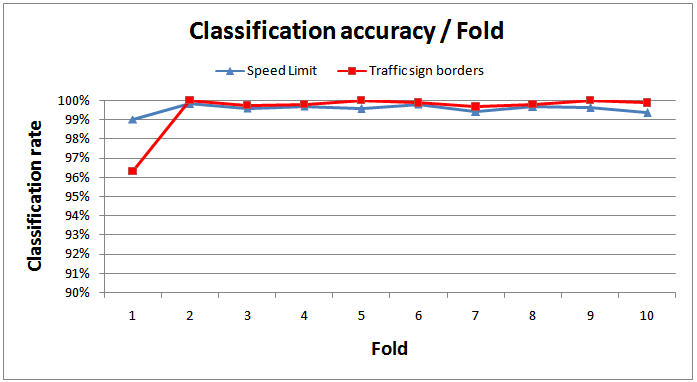 | Figure 4. Classification rateachieved in different folds |
 | Figure 5. Samples of the rotated signs used in the testing of the multi-class AdaBoost |
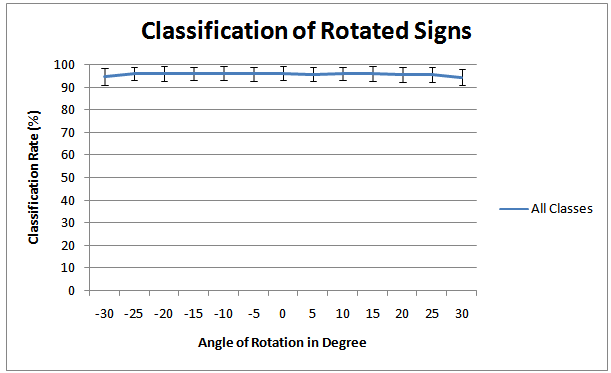 | Figure 6. Average classification rate versus rotation angle of traffic signs |
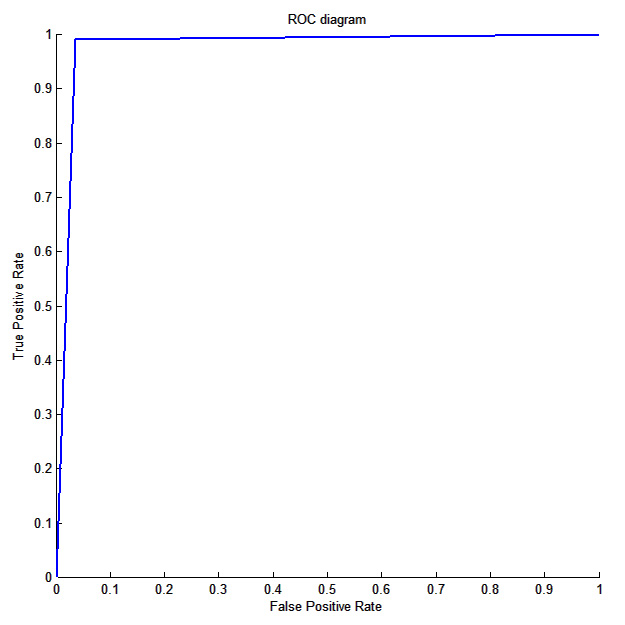 | Figure 7. ROC diagram of the multi-class AdaBoost |
5.2. Classification of Standard Datasets
- In order to achieve realistic empirical comparison with state of the art, the proposed approach is tested with 8 standard datasets from UCI and KEEL machine learning repository[26; 27], as depicted in Table 3. As a standard criterion, 10-fold cross validation is employed and the results of all folds are averaged. Figures 8-15 show the error rate of the different datasets employed in the test. In general, the proposed multi-class AdaBoostshows very goodperformance and generalization for all datasets except for Yeast. The same results regarding Yeast dataset was reported by Jun and Ghosh[28]. As indicated by Jun and Ghosh, the low classification performance in the case of Yeast dataset can be caused by the high unbalance of this dataset. Out of 1484 examples the Yeast dataset consists of, there are only 5 examples in the smallest class. They also reported performance degradation in the case of Page blocks dataset for the case of AdaBoost.MI. On contrary, the performance of the proposed classifier in this dataset is quite high.The proposed classifier performs better than the one proposed by Zhu et al.[18] for the case of Segment dataset. However, the results concerning other dataset are better than what were reported for AdaBoost.MH.The average training and testing time required for running 1 fold which consists of 100 rounds is also depicted in Table 3. The benchmark testing of both experiments is achieved using Dell Latitude E6400. The training complexity of the proposed approach for N classes is given by O(A.N), where A is the complexity for binary training of AdaBoost. The root node has the highest A due to the presence of all the data in the classification. As proceed in the BDT, the complexity A will decrease. For testing, the algorithm complexity will be O(B.log2N) where B is the complexity of testing a new data point by the classifier.
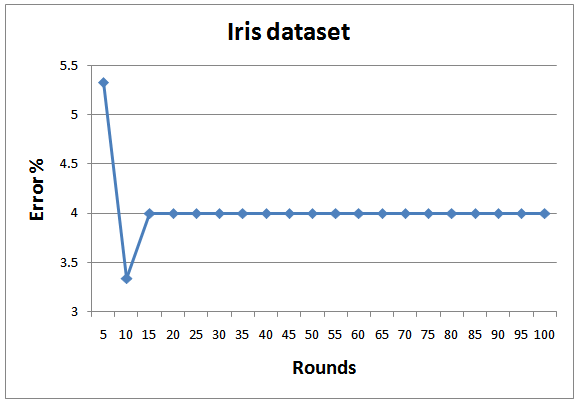 | Figure 8. Testing errors for Iris dataset |
|
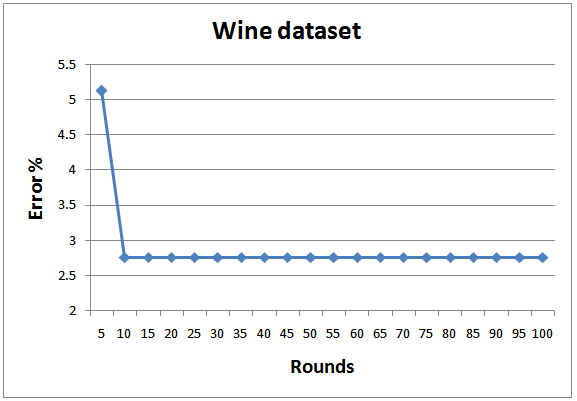 | Figure 9. Testing errors for Wine dataset |
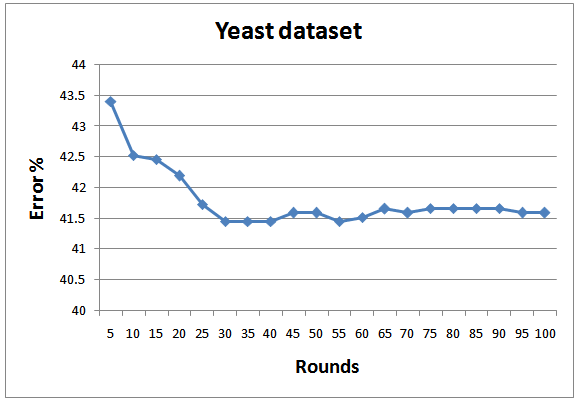 | Figure 10. Testing errors for Yeast dataset |
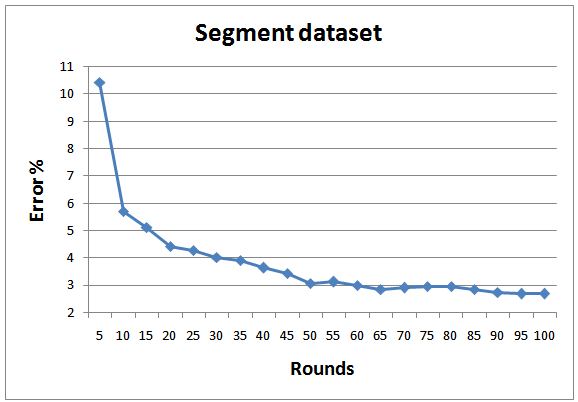 | Figure 11. Testing errors for Segment dataset |
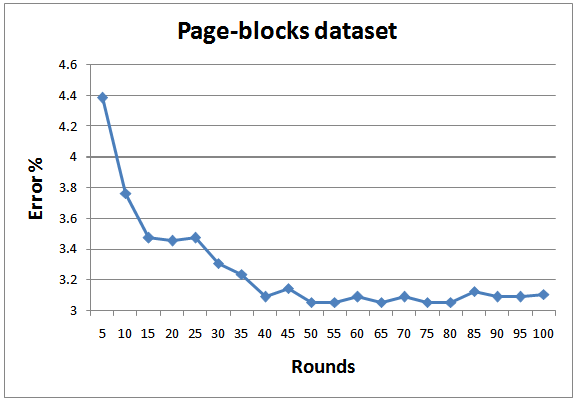 | Figure 12. Testing errors for Page-blocks dataset |
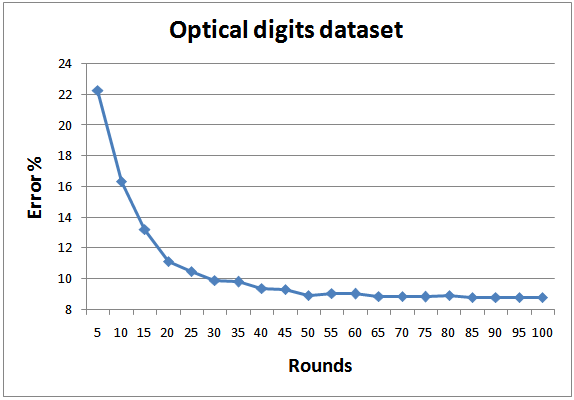 | Figure 13. Testing errors for Optical digits dataset |
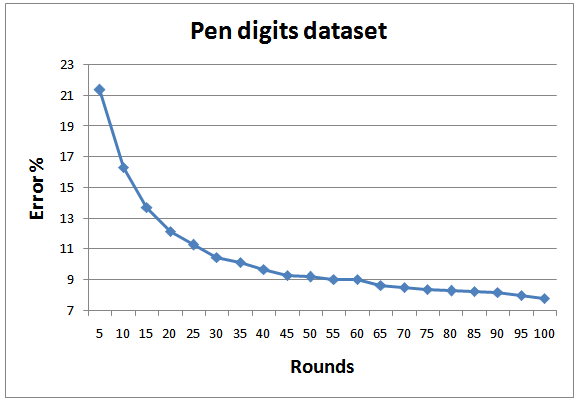 | Figure 14. Testing errors for Pen digits dataset |
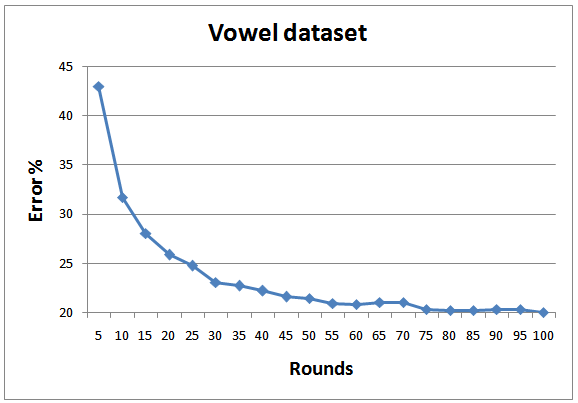 | Figure 15. Testing errors for Vowel dataset |
6. Conclusions
- This paper proposed a multi-class AdaBoost classifier based onen ensemble of binary AdaBoosts arranged as binary decision tree. The proposed approach adaptively combines each of binary classifiers at each node of theBDTto form the desired classifier.The technique was tested in two different ways. The proposed classifier was evaluated using a set of binary traffic sign imagesfor traffic sign recognition application. The proposed classifier performs better than the comparison one as it achieved better recognition accuracyand it is much faster.It is also evaluated using 8 standard datasets from UCI and KEEL. The proposed classifier converged to very reliable solutions to the datasets under test as well as good and fast generalization.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML