-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Intelligent Systems
p-ISSN: 2165-8978 e-ISSN: 2165-8994
2013; 3(1): 33-39
doi:10.5923/j.ajis.20130301.05
Fuzzy Time Series Method Based on Multiplicative Neuron Model and Membership Values
Erol Egrioglu1, CagdasHakan Aladag2, Ufuk Yolcu3, Burcin Seyda Corba1, Ozge Cagcag1
1Department of Statistics, University of OndokuzMayis, Samsun, 55139, Turkey
2Department of Statistics, Hacettepe University, Ankara, 06800, Turkey
3Department of Statistics, Giresun University, Giresun, 28000, Turkey
Correspondence to: Erol Egrioglu, Department of Statistics, University of OndokuzMayis, Samsun, 55139, Turkey.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Many fuzzy time series forecasting methods have been suggested to forecast time series in the literature. Most of these methods use various artificial intelligence methods. The determining of the fuzzy relation is one of the most important stage in fuzzy time series methods. Some methods determine fuzzy relations by using index number of the fuzzy sets. Recently, several methods that use membership values to determine fuzzy relation have been proposed in the literature. In this paper, a new fuzzy time series forecasting algorithm is proposed. The algorithm use fuzzy c-means method in fuzzification stage. The determining of fuzzy relations stage is performed by multiplicative neuron model in proposed algorithm. In the proposed method, membership values are used instead of index number of the fuzzy sets. Three data sets are used to compare proposed method with some other methods in the literature. It is concluded that proposed method outperforms the some other methods in the literature.
Keywords: Fuzzy Time Series, Forecasting, Multiplicative Neuron Model, Fuzzy C-means
Cite this paper: Erol Egrioglu, CagdasHakan Aladag, Ufuk Yolcu, Burcin Seyda Corba, Ozge Cagcag, Fuzzy Time Series Method Based on Multiplicative Neuron Model and Membership Values, American Journal of Intelligent Systems, Vol. 3 No. 1, 2013, pp. 33-39. doi: 10.5923/j.ajis.20130301.05.
Article Outline
1. Introduction
- Fuzzy time series methods are based on fuzzy set theory that was proposed by Zadeh[1]. For some time series, the observations of time series can be represented by fuzzy sets. If the observations of the time series are fuzzy sets, traditional time series methods cannot be used. Time series that have got fuzzy observations are called fuzzy time series. The fuzzy time series firstly were defined by Song and Chissom[2]. Moreover, the first fuzzy time series forecasting method was proposed by Song and Chissom[3]. There are two kind of fuzzy time series as time variant and time invariant. The inner relations of time invariant fuzzy time series do not change in time. In generally, fuzzy time series methods have got three stages. These stages are called fuzzification, determining fuzzy relation and deffuzzification, respectively. Various artificial intelligence methods can be used in these stages. Genetic algorithm, particle swarm optimization and fuzzy c-means methods for fuzzification of time series; genetic algorithm, particle swarm optimization and artificial neural networks for determining fuzzy relation and artificial neural networks for defuzzification have been used in the literature. it is known that each stages are very effective on forecasting performance of fuzzy time series.Artificial neural networks were firstly used for determining fuzzy relation by Huarng and Yu[4]. They determined fuzzy relation by using artificial neural networks in first order fuzzy time series forecasting model. Then, Yu and Huarng[5] applied neural networks to fuzzy time series forecasting in bivariate first order fuzzy time series forecasting model. Artificial neural networks were applied to determine fuzzy relation by Egrioglu et al.[6] in bivariate high order fuzzy time series forecasting model. Egrioglu et al. ([7-8]), Aladag et al. ([9-10]) ,Egrioglu et al.[11], Aladağ[12], Yu and Huarng[13] and Yolcu et al.[14]. Egrioglu et al. ([6-7-8]), Aladag et al. ([9-10]), Egrioglu et al.[15], Aladağ[16] used index number of fuzzy sets for training artificial neural networks in determining fuzzy relations stage. In these studies, membership values of fuzzy sets are not taken into consideration. Yu and Huarng[13] and Yolcu et al.[14] used membership values of fuzzy sets for training artificial neural networks in determining fuzzy relations stage. Aladağ[16] different from others since it used multiplicative neuron model neural network instead of multilayer perceptron neural network. The multiplicative neuron model neural network was use to determine fuzzy relation of seasonal fuzzy time seires in Aladağ S. et al.[12].In this study, novel fuzzy time series method is proposed. Proposed method use fuzzy c-means clustering in fuzzification stage and multiplicative neuron model neural network in determining fuzzy relations stage. Particle swarm optimization method is applied for training multiplicative neuron model neural network. Fuzzy c-means, multiplicative neuron model neural network and particle swarm optimization are summarized respectively in section 2,3 and 4. In section 5, the proposed method is given. Applications of proposed method and conclusions are given in section 6 and in section 7.
2. The Fuzzy C-means Clustering Method
- Song and Chissom[2] suggested partition of universe of discourse method for using the fuzzification stage. However there are several problems such as determination of the number of intervals, arbitrarily choice of interval length and membership degrees in this method. To solve these problems, Cheng et al.[17] and Li et al.[18] used fuzzy c-means clustering method for fuzzification. This method that is commonly used for clustering was firstly introduced by Bezdek[19]. It is based on objective function and advantage of this method is objects can have membership degrees in clusters. In this method, fuzzy clustering is conducted by minimizing the least squared errors within groups. Fuzzy c-means clustering algorithm has two main steps. In the first step, the algorithm finds centroids of each cluster and in the next step every object is assigned to a cluster depending on its distance to centroids. Let uij be the membership values, vi be the center of cluster, n be the number of variables, and c be the number of clusters. Then the objective function, which is tried to be minimized in fuzzy clustering, is
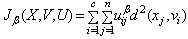 | (1) |
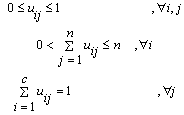 In fuzzy c-means clustering method, to solve the minimization problem given above, an iterative algorithm is used. In each iteration, the values of viand uij are updated by using the formulas given in (3) and (4), respectively.
In fuzzy c-means clustering method, to solve the minimization problem given above, an iterative algorithm is used. In each iteration, the values of viand uij are updated by using the formulas given in (3) and (4), respectively.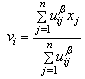 | (2) |
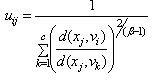 | (3) |
3. Particle Swarm Optimization
- Particle swarm optimization is one of the heuristic technique that first devoloped by Kennedy and Eberhart[20]. Although a general problem with optimization algorithms is that of becoming trapped in a local optimum, particle swarm optimization avoid from it.In the literature, particle swarm optimization method has been applied for fuzzification stage in fuzzy time series. Davari et al.[21] was applied PSO algorithm for fuzzification stage in the first order fuzzy time series forecasting model. Then Kuo et al. ([22-23]) used particle swarm optimization method in high order models and in both first and high order models, respectively. Particle swarm optimization method was used for two factor high order model in Park et al.[24]It was shown that using some time varying parameters can increase the convergence speed of the algorithm. Shi and Eberhart[25] used time varying inertia weight. Time varying acceleration coefficient in standard particle swarm optimization method was applied by Ma et al.[26]. In modified particle swarm optimization, these time varying constituents are used together unlike standard particle swarm optimization.Algorithm 1: The modified particle swarm optimization.Step 1.Positions of each kth (k = 1,2, …, pn) particles’ positions are randomly generated in the initial satge and kept in a vector Xk given as follows:
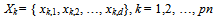 | (4) |
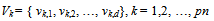 | (5) |
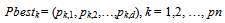 | (6) |
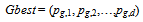 | (7) |
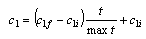 | (8) |
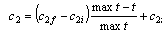 | (9) |
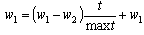 | (10) |
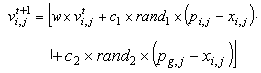 | (11) |
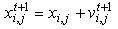 | (12) |
4. Multiplicative Neuron Model
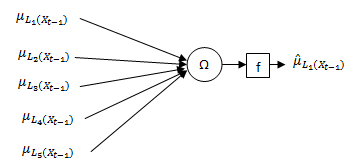
- The single multiplicative artificial neuron model which is a special case of neuron model was first presented by Yadav et al.[27]. This model has only one neuron and the general structure of the model, which includes only five inputs is illustrated in Figure 1.
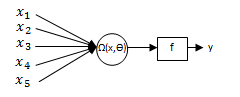 | Figure 1. Single multiplicative artificial neuron model |
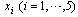 is input pattern and when output values are computed by using multiplication function instead of sum function .The operator
is input pattern and when output values are computed by using multiplication function instead of sum function .The operator 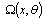 is a multiplicative operation which is composed of multiplication of weighted inputs. Activation function and target of the model are represented by f and y, respectively. In the literature, for training the multiplicative neuron model, there are several learning algorithms. Back propagation and cooperative particle swarm optimization learning algorithms were used in the process of multiplicative neuron model, Yadav et al[27] and Zhao and Yang [28], respectively.
is a multiplicative operation which is composed of multiplication of weighted inputs. Activation function and target of the model are represented by f and y, respectively. In the literature, for training the multiplicative neuron model, there are several learning algorithms. Back propagation and cooperative particle swarm optimization learning algorithms were used in the process of multiplicative neuron model, Yadav et al[27] and Zhao and Yang [28], respectively.5. Proposed Method
- In the literature, various techniques have been applied to determine fuzzy relations in fuzzy time series forecasting methods. These techniques are fuzzy logic group relation tables, genetic algorithm, particle swarm optimization and neural networks. Some of these methods passed over membership values of fuzzy sets. The memberships of fuzzy sets should be taken into consideration in determining fuzzy relation stage. In this study, a novel fuzzy time series forecasting method is proposed. Fuzzy c-means clustering in fuzzification stage and multiplicative neuron model neural network in determining fuzzification stage are used in this method. To train multiplicative neuron model neural network, particle swarm optimization is applied. The some advantages of proposed method are given as below:•Because of using fuzzy c-means in fuzzification stage, there is no necessity subjective decisions like determining interval length.•The proposed method take into consideration membership values.•The proposed method has modeling ability of multiplicative neuron neural network.•The proposed method can forecast nonlinear time series because multiplicative neuron neural network are employed.The proposed method is given in algorithm 2.Algorithm 2: Proposed MethodStep 1. Apply FCM.Firstly, FCM presented in Section 2 with the number of clusters c (
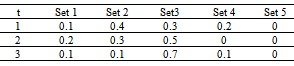
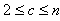 ) is applied to time series includes crisp values. Values of cluster centers are calculated then, values of memberships are obtained by using these values of cluster centers. Sorted fuzzy clusters Lr, r=1,2, …, c are obtained by sorting the cluster centers in ascending order. The membership values are sorted by same order.Step 2. Rearrange membership values .Firstly, threshold value (tv1) are chosen. Then, the membership values that are lower than threshold value are taken as zero. For the each observations, membership values are standardized. For example, for any t, membership values are given in Table 1 when five fuzzy sets are used.
) is applied to time series includes crisp values. Values of cluster centers are calculated then, values of memberships are obtained by using these values of cluster centers. Sorted fuzzy clusters Lr, r=1,2, …, c are obtained by sorting the cluster centers in ascending order. The membership values are sorted by same order.Step 2. Rearrange membership values .Firstly, threshold value (tv1) are chosen. Then, the membership values that are lower than threshold value are taken as zero. For the each observations, membership values are standardized. For example, for any t, membership values are given in Table 1 when five fuzzy sets are used.
|
|
|
|
 | Figure 2. The architecture of multiplicative neuron model for first fuzzy set |
6. Application
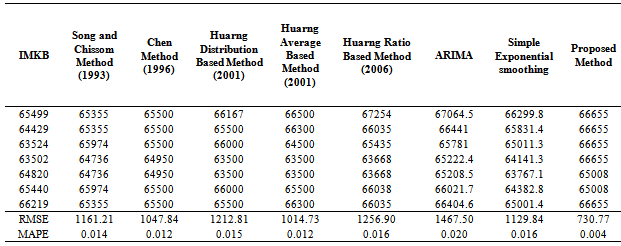
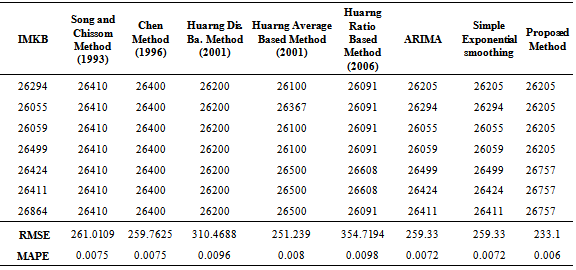
- Firstly, the data of Index 100 in stocks and bonds exchange market of İstanbul (IMKB) between 01/10/2010 and 23/12/2010 are used in the application. The time series graph of the data set is given in Fig.3. The last 7 observations are used for testing, the other observations are used as training set.
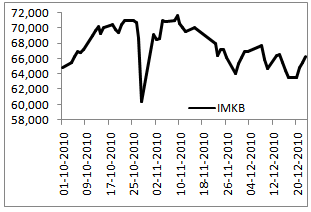 | Figure 3. The time series graph of IMKB, the period between 01.10.2010 and 23.12.2010 |
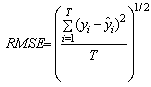 | (13) |
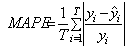 | (14) |
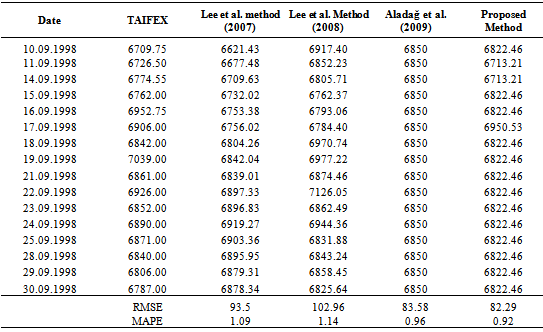
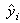 is the predicted value; T is the number of data.The proposed method and benchmark methods are applied to TAIFEX data whose observations are between 03.08.1998 and 30.09.1998. The time series, which is also used in Lee at al.[30] has 47 observations. The first 31 and the last 16 observations are used for the training and the test sets, respectively. TAIFEX data is also forecasted by using proposed method. The results of other methods are taken from Lee et al. ([30-31]) and Aladag et al.[9]. The all results for TAIFEX data are shown in Table 6.In the application of the proposed method, th1= 0.05 and th2=0.05, the best number of fuzzy sets is obtained as 8.
is the predicted value; T is the number of data.The proposed method and benchmark methods are applied to TAIFEX data whose observations are between 03.08.1998 and 30.09.1998. The time series, which is also used in Lee at al.[30] has 47 observations. The first 31 and the last 16 observations are used for the training and the test sets, respectively. TAIFEX data is also forecasted by using proposed method. The results of other methods are taken from Lee et al. ([30-31]) and Aladag et al.[9]. The all results for TAIFEX data are shown in Table 6.In the application of the proposed method, th1= 0.05 and th2=0.05, the best number of fuzzy sets is obtained as 8.
|
|
|
7. Discussion and Conclusions
- Some fuzzy time series methods passed over membership values. Recent years, fuzzy time series methods based on membership values have been proposed in the literature. In this study, a novel fuzzy time series forecasting method that take into consideration membership values are proposed. The performance of the proposed method is experimentally compared with the other methods by using three real time series data. It is obtained from experimental study that the forecasting of the proposed method is better than benchmark methods for two time series. Besides good forecasting performance of the proposed method, it has got ability to forecast nonlinear time series because of employing multiplicative neuron model neural network. In the future studies, threshold parameter can be optimized in the PSO algorithm. This optimization may provide better forecasting results.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML