1. Introduction

According to[1], a computer network intrusion is defined as any set of actions that attempt to compromise the integrity, confidentiality or availability of a network resource. In general, intrusion attempts are external malicious actions that have the purpose of intentionally violating the system security properties. Complete or partial intrusion is a result of successful attacks, which exploit the system vulnerabilities. Since invulnerable computer networks are practically impossible of achieving, it is more reasonable to assume that intrusions can happen. In this way, the main challenge in network security is to determine if any network action is either normal or intrusion suspicion.

In complex domains, such as network Intrusion Detection System (IDS), a huge amount of activity data is collected from the network generating large log files and raw network traffic data, in which human inspection is impossible. Thus, these activity data must be compressed into high-level events, called attributes. After it, a set of attributes is obtained and monitored by the IDS in order to detect intrusion attempts.

However, there are some attributes with false correlations, hiding the underlying process, and other that may be either irrelevant or redundant (its information is somehow included in other attributes). In this way, removing these attributes, or rather, selecting an optimal attributes set that adequately describes the network environment are essential in order to achieve fast and effective response against attack attempts, reduce the complexity and the computation time, and increase the precision of the IDS[2]. In this way, development of methods for selecting optimal attributes is welcome.

In this work, it is investigated some attribute selection approaches through a comprehensive comparison of C4.5 decision-tree model based on Shannon entropy[3] with other three attribute selection methods (proposed by the authors in previously papers), namely, C4.5 based on Rényi entropy[4], C4.5 based on Tsallis entropy[5] and an approach that combines Shannon[6], Rényi and Tsallis entropies.

In order to evaluate the classification performance of these methods, it was considered four attack categories (DoS, Probing, R2L and U2R) based on KDD Cup 1999 data[7], and the following classification models: CLONal selection ALGorithm (CLONALG)[8], Clonal Selection Classification Algorithm (CSCA)[9] and Artificial Immune Recognition System (AIRS)[10].

Experimental results show that the classification efficiency of optimal attributes subset based methods is comparable to that based on complete attributes set for CLONALG and CSCA classification models.

The paper is organized as follows. Section II provides more detail information about the attribute selection methods. The data set, classifiers, and performance metrics used in the experiments are described in Section III. Results are reported in Section IV and conclusions are shown in Section V.

2. Attribute Selection

Attribute selection is a strategy of removing irrelevant and redundant attributes in order to avoid performance degradation (for instance, speed, detection precision, etc.) of algorithms of data characterization, rule extraction, designing of predictive models, and others.

Considering a given dataset that can be characterized by N attributes, the objective of any attribute selection process is to find a minimum number M of optimal attributes that are capable of describing the dataset as well as with N attributes in such a way that the characteristic space is reduced according to some criterion[11].

Attribute selection can be categorized as filter or wrapper model. The filter model consists in selecting attributes independently of the chosen learning algorithm by examining intrinsic characteristics of the data and by estimating the quality of each attribute considering only the available data. In contrast, the wrapper model consists in evaluating the attributes subset performance by applying a predetermined learning algorithm on the selected attributes subset. In this way, for each new attributes subset, the wrapper model needs to learn the classification algorithm and, based on its performance, to evaluate and determine which attributes should be selected. In general, this model finds the best attributes considering the predetermined classification algorithm resulting in better learning performance, but it shows to be more computationally expensive than the filter model[12].

Since there are 2^N possible subsets considering N attributes, an exhaustive search for an optimal attributes subset may be impracticable, especially when N and the number of data classes is increased. Therefore, heuristic methods that explore reduced search space are commonly used for attribute selection. These methods are typically greedy in the sense that they make a locally optimal choice in the hope that this choice will lead to a globally optimal solution. In practice, such greedy methods are effective in estimating optimal solution[11].

For its turn, Decision Trees are supposed to be effective classifiers in a large variety of domains. Most of decision tree algorithms use standard top-down greedy approach. The learning process of decision trees is based on an induction process where is used training dataset described in terms of attributes. The decision tree result is a directed graph where each internal node denotes a test on the selected attribute, each branch represents an outcome of the respective test and each leaf node corresponds to a class label, as shown in Figure 1.

Initially, considering the complete set of attributes, the decision tree algorithm selects an optimal attribute based on some criterion that partitioning the data into subsets according to the attribute values. Next, this process is recursively applied to each partitioned subsets and it is finished when a leaf node is obtained, i.e., the data in the current subset belongs to the same class.

In our attribute selection approach, a decision tree induction is used for attributes selecting. In this way, the attributes that do not appear in the designed decision tree are considered irrelevant. Consequently, the attributes that corresponds to the internal nodes are selected to form the optimal attributes subset.

Figure 1. Decision tree induction for attribute selection

The most popular decision tree algorithms are the ID3 (Induction of Decision Tree)[13] and its successor, the C4.5 algorithm[3]. Using a top-down process, both algorithms are capable of designing decision trees by selecting appropriate attribute for each decision node based on Shannon entropy measure[6].

Specifically, in ID3 algorithm, the best attribute in each iteration step is that with highest mutual information among all others. Although achieving good results, it presents high bias in favor of attributes with large span of values. To try to solve this problem, Quinlan proposed the C4.5 algorithm comprising of a normalization stage, called gain ratio, in which the apparent gain assigned to large span attributes is adjusted by it[3]. For more details about C4.5 decision trees, see[14].

As known, there are others entropy measures, such as Rényi and Tsallis entropies. In theory, they can be applied in attributes selection schemes. Hence, it is described in this paper an empirical investigation in order to assess whether these entropy measures are adequate in designing attributes selection schemes. In the next sections, Shannon, Rényi and Tsallis entropies are duly described.

2.1. Shannon Entropy

Entropy is a statistical measure related with the amount of information into a random variable. Based on the original paper of Shannon[6], given a class random variable C with discrete probability distribution , where 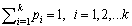and c_i is the ith outcome class. Then, the entropy H(C) is the expected amount of information needed for class prediction, defined as:

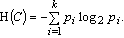(1)

Now considering a set of N attributes A_i, where i = 1, ... N and each attribute A_i can assume v_i finite values, Shannon has defined other basic concept in information theory, the mutual information, I(C;A_i) that measures the dependence between two random variables, in our case C and A_i. I(C;A_i) is expressed in terms of Shannon entropy as:

(2)

where H(C| A_i) stands for the conditional entropy of C given A_i. The mutual information can be interpreted as the amount of uncertainty from C which is decreased by the knowledge of A_i.

Other entropies measures have been proposed as, for instance, Rényi[4] and Tsallis[5]. Rényi and Tsallis entropies are based on an additional parameter α used to make them more or less sensitive to the considered probability distribution shapes.

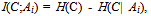2.2. RÉNyi Entropy

The Rényi entropy constitutes a measure of information of order α, having Shannon entropy as the limit case, and is defined by:

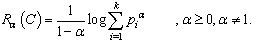(3)

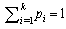where and .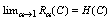

Using Rényi entropy of order α ϵ (0, 1), the mutual information can be given as:

(4)

2.3. Tsallis Entropy

Another generalized entropy, defined by Constantino Tsallis[5], is given by:

(5)

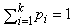where and .

For α > 1, Tsallis mutual information is defined as[15]: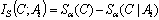

(6)

Using Shannon entropy, events with high or low probability have no different weights in the entropy computation. However, using Tsallis entropy, for α > 1, events with high probability contributes more than low probabilities ones. Hence, the higher is the value of α, the higher is the contribution of high-probability events. In the same way, increasing the values of α (α → ∞), Rényi entropy is increasingly determined by events with higher probabilities, and lowering the values of α (α → 0), the events are more equally, regardless their probabilities[16].

2.4. Proposed Attribute Selection Schemes

In this work, aiming to select an optimal attributes subset, four different approaches in order to identify four attacks categories have been considered. In addition, it was considered the filter model based attribute selection. In this way, it was designed C4.5-based decision trees, i.e., gain ratio was considered, taking account Rényi entropy versus Shannon entropy and Tsallis entropy versus Shannon entropy. Moreover, it was designed C4.5-based decision trees considering a combination (ensemble) of Shannon, Rényi and Tsallis entropies. The proposed attribute selection schemes are shown in Figure 2.

Figure 2. Attribute selection schemes

The ensemble approach combines the results from the individual attribute selection schemes in order to improve the selection of optimal attributes subset by avoiding relying only on a single approach.

3. Simulation Environment

In order to evaluate the proposed attributes selection schemes and to design the classification models, it was used the WEKA toolkit (Waikato Environment for Knowledge Analysis)[17].

In WEKA, the source code of the class J48 for generating standard-C4.5 based decision tree was modified by the authors using JAVA programming language, replacing Shannon entropy by α-dependent Rényi and/or Tsallis entropies.

3.1. Data Set Description

In general, to evaluate IDS schemes, dataset benchmarks are used as, for instance, the intrusion dataset available in Knowledge Discovery and Data Mining Competition - KDD Cup 99[7] for both training and testing. This dataset is still used by researchers because it has the capability to compare different intrusion detection techniques on a common dataset base.

In the KDD99 database, any network connection (or instance) is comprised of 41 attributes and each instance is labeled either as normal or as an attack-specified type. These attributes are shown in Table 1 and its meaning can be found in[7].

In KDD99 database, there are 494,021 instances in which 97,278 are considered normal and 396,744 are labeled as attacked by 22 different types that can be classified in 4 main categories as follows:

• Denial of Service (DoS) – attacks from this category lead to deny of legitimate requests usually by network flooding, which is defined as a very large amount of connections to the same host in a very short time.

Table 1. Network attributes and their respective number used in this work Nr. Attribute Nr. Attribute 1 Duration 22 is_guest_login 2 protocol_type 23 count 3 service 24 srv_count 4 flag 25 serror_rate 5 src_bytes 26 srv_serror_rate 6 dst_bytes 27 rerror_rate 7 land 28 srv_rerror_rate 8 wrong_fragment 29 same_srv_rate 9 urgent 30 diff_srv_rate 10 hot 31 srv_diff_host_rate 11 num_failed_logins 32 dst_host_count 12 logged_in 33 dst_host_srv_count 13 num_compromised 34 dst_host_same_srv_rate 14 root_shell 35 dst_host_diff_srv_rate 15 su_attempted 36 dst_host_same_src_port_rate 16 num_root 37 dst_host_srv_diff_host_rate 17 num_file_creations 38 dst_host_serror_rate 18 num_shells 39 dst_host_srv_serror_rate 19 num_access_files 40 dst_host_rerror_rate 20 num_outbound_cmds 41 dst_host_srv_rerror_rate 21 is_host_login

Table 2. Attacks per Category DOS PROBING R2L U2R back (1026) ipsweep (586) ftp-write (8) loadmodule (10) land (11) nmap (151) guess-passwd (53) rootkit (7) neptune (10401) portsweep (155) imap (11) perl (3) pod (69) satan (16) multihop (11) normal (1676) smurf (7669) normal (1704) phf (5) buffer-overflow teardrop (15) spy (4) (21) normal (2573) wareszclient (60) warezmaster(20) normal (1934)

• Probing - It is an attack category based on scanning of the network in order to get information or vulnerabilities. Probing actions is based on sending a huge amount of packets to different hosts in a short time with very short duration.

• Remote to Local (R2L) - attacks from this category can be characterized by attempts of remote-machine user to get access to a local server.

• User to Root (U2R) - It is an attack category characterized when an authorized user tries to get access as super user (root).

Usually, network traffic data samples are necessary to be collected in advance to design an intrusion detection system. However, complete attack information is very difficult to obtain because, in real world, intruders constantly develop new attack methods in order to exploit system security vulnerabilities. Since, in general, the collected samples always present some uncertainty, as only limited information about intrusive activities is available, a subset of attack from each category was randomly selected from KDD99 database in order to simulate the uncertainty problem and to decrease computational cost without compromises the research results. As shown in Table 2, each category contains instances corresponding to attack types and normal behavior and its individual amount is shown in brackets.

3.2. Performance Metrics

In a binary classification problem aiming to distinguish normal behavior patterns (positive) or suspicious attack patterns (negative), any classifier is supposed to label instances as either positive or negative. The classifier decisions can be represented in a structure, known as a confusion matrix. The confusion matrix has four categories: true positive (TP) (i.e., positive instances classified correctly as normal), false positive (FP) (i.e., negative instances classified as normal), true negative (TN) (i.e., negative instances classified correctly as attacked), and false negative (FN) (i.e., positive instances classified as attacked).

The amount of instances from the database (outcomes) forms the basis for several other performance measures that are well known and commonly used for classifier evaluation. Therefore, the analysis of the proposed attributes selection approaches described previously was carried out by means of the performance measures explained below.

The Area Under Receiver Operating Characteristic (ROC) Curve, called AUC, is a single-value measurement originated from signal detection field and has been widely used to measure classification model performance[18]. The value of the AUC ranges from 0 to 1. The ROC curve is used to characterize the trade-off between true positive rate, , and false positive rate, 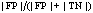. It provides an effective way for performance comparison among classifiers of imbalanced datasets. A classifier that gives a large area under the ROC curve is preferable over a classifier with a smaller area under the curve. A perfect classifier provides an AUC equals to 1.

For its turn, the Kappa statistic is a method that compensates random hits[19]. This is originally a measure of agreement between two classifiers. However, it is employed as a classifier performance measurement because it considers random successes as a standard[20].

The value of the Kappa statistic ranges from 0 (total disagreement) to 1 (perfect agreement) and it is less expressive than ROC curves when applied to binary classification. However, for multiple class problems, the Kappa statistic is very useful for measuring the accuracy of the classifier while compensating random successes.

The Kappa statistic is an alternative to classification rate, CR = |TP|/(|TP|+|FN|+|FP|+|TN|) or, simply, CR = #of_instances_classified_correctly/#of_instances). The main difference between CR and the Kappa statistic is the scoring of the correct classifications. CR scores all the successes over all classes, whereas the Kappa statistic scores the successes independently of the class. The latter is less sensitive to randomness caused by the different number of instances in each class.

3.3. Classifiers - AIS algorithms

The Artificial Immune System (AIS) is the class of adaptive computational algorithm that emulates processes and mechanism inspired from biological immune systems. These algorithms use learning, memory, and optimization capabilities of the immune system to develop computational tools for classification, optimization, pattern recognition, novelty detection, process control, among others. AIS is supposed to develop adaptive systems capable of solving problems at different domains[21].

In this work, the classification performance is obtained considering the following classification models: clonal selection algorithm – CLONALG[8], clonal selection classification system – CSCA[9] and artificial immune recognition system – AIRS[10]. These algorithms simulate the antigen-antibody recognition process by evolving a population of B-cells in order to recognize antigens (suspicious attack patterns from the training set). They are applied in the attribute subsets selected by the four proposed attribute selection approaches.

The CLONALG is based on clonal selection theory as proposed in[8]. Its goal is to develop a memory set of antibodies that represents a solution for a specific problem. It describes the basic feature of an immune response against an antigenic stimulus that consists on the fact that only those cells that recognize any antigens are selected to proliferate. The selected cells are subject to an affinity maturation process, which improves their affinity capability with the antigens. The CLONALG was implemented by Brownlee[9] in WEKA toolkit.

The CSCA was developed by Brownlee[9] and is formulated as a fitness function that maximizes the number of patterns classified correctly and minimizes misclassification. In CSCA, many generations are carried out and, in each generation, the entire set of antibodies is exposed to all antigens.

Finally, the AIRS, a supervised learning algorithm that is used for classification problems, was proposed in 2001[22]. The AIRS[10] is a clonal-selection-inspired procedure that perform cloning and somatic hypermutation for maturating a set of recognition cells (or memory cells) which are representative of the training data that the model was exposed to. It is suitable for classifying unobserved cases and it uses a single iteration on a set of training dataset.

In the AIRS algorithm, any B-cell is defined as an Artificial Recognition Ball (ARB) that consists of an antibody that indicates: the class it belongs, the number of resources held by the cell, and the current stimulation value of the cell (defined as the similarity between the ARB and an antigen). The ARB population is trained during several cycles of competition for limited resources. The best ARBs receive the highest number of resources, and no-resource ARBs are eliminated from the population. In each training cycle, the best ARB classifiers generate mutated clones that enhance the antigen recognition process, whereas the ARBs with insufficient resources are removed from the population. After training, the best classified ARB are selected as memory cells, and they are used to classify novel antigens.

The so-called AIRS1, the first version of the AIRS, performs its tasks using data reduction. This means that it does not use the complete training data for generalization and the resulted classifier represents the training data with reduced or minimum number of instances. It was adopted in this work. Other versions have been presented (e.g. AIRS2, parallel AIRS2), but they did not be tested in this work due the high volume of the datasets, which generate a high increase overall runtime.

4. Experimental Results

Considering the previously experimental simulations results obtained by the authors, shown in[14], where it was designed decision trees based on Shannon, Rényi and Tsallis entropies, here was chosen the best designed decision trees in terms of classification efficiency and tree size. For example, the decision tree designed by Rényi entropy with α = 0.5, and the decision tree designed by Tsallis entropy with α = 1.2 were selected considering the DoS category.

After choosing the decision trees, a subset of attributes was individually selected for each dataset according to individual category of attacks. Moreover, a new attributes subset was selected based on the ensemble approach extracted by using of Shannon, Rényi and Tsallis entropies.

Table 3. Selected attributes by Shannon, Rényi and Tsallis information measures Category Measures Selected Attributes DoS Shannon 2, 5, 7, 8, 23, 34, 36, 39 Rényi 2, 5, 7, 8, 23, 32, 35, 36, 39 Tsallis 2, 5, 7, 8, 23, 26, 34, 39 Probing Shannon 1, 2, 4, 5, 6, 23, 30, 33, 37, 38, 40 Rényi 1, 2, 5, 6, 25, 30, 32, 33, 37, 38, 40 Tsallis 1, 2, 4, 6, 23, 30, 31, 33, 37, 38, 40 R2L Shannon 1, 3, 5, 6, 9, 10, 11, 17, 19, 22, 32, 33, 35 Rényi 2, 5, 6, 10, 11, 12, 19, 33, 35, 37, 38, 39 Tsallis 1, 3, 5, 6, 10, 11, 17, 19, 22, 37, 38 U2R Shannon 13, 16, 17, 18, 32, 33 Rényi 13, 18, 32, 33, 36 Tsallis 13, 16, 18, 32, 33

Since different attack categories may have different optimal attribute subsets, four experiments have been performed in order to evaluate the attribute subsets that are more suitable for detecting individual category of attacks according to a given entropy formulation. The experimental results are shown in Table 3. The attributes subsets selected by the ensemble approach are shown in Table 4.

Table 4. Selected Attributes for Individual Attack Category by the Ensemble Attribute Selection Technique Category Selected Attributes DoS 2, 5, 7, 8, 23, 26, 32, 34, 35, 36, 39 Probing 1, 2, 4, 5, 6, 23, 25, 30, 31, 32, 33 R2L 1, 3, 5, 6, 9, 10, 11, 12, 17, 19, 22, 32, 33, 35, 37, 38, 39 U2R 13, 16, 17, 18, 32, 33, 36

As can be seen in Table 3, as expected, some selected attributes are different for different attack categories, because different types of attack have evidently their own patterns. In addition, it is important to notice that attributes 20 and 21 do not show any variations in the data set. Thus, they have no relevance to intrusion detection.

4.1. Experimental Result Analysis

In the experimental procedures, the first three classification models are applied to the original data sets (with 41 attributes) in order to obtain classification performance on the testing instances. Next, the classification results of these algorithms are used to compare the effectiveness of the four proposed attribute selection techniques. The criteria used to evaluate the effectiveness of the selected attributes are kappa statistic[19] and AUC. The result is shown in Table 5.

The experiments were carried out using ten-folds cross validation approach to control their validation. User-defined parameters for each algorithm have been optimized to achieve the best possible classification accuracy. The experimental results were obtained considering the network-traffic training data sets described in Table 2.

Analyzing the experimental results on the attribute selection schemes performance, it is observed that they are significantly different at the 1%-level (whether the difference is statistically significant). Furthermore, the performance values have varied depending on both the classifiers and the performance metric used to evaluate the models.

The attribute selection has decreased significantly the number of attributes and data dimensionality, leading to a better performance of the AIS algorithm, resulting in lesser running time compared to the situation when the complete attributes set of the original database was used.

From the Table 5, the detection results on KDD 99 dataset indicate that the performance remains almost the same or even becomes better for CLONALG and CSCA classification models designed considering DoS, R2L and U2R datasets by any attribute selection technique compared when the complete data set (with 41 attributes) is used.

In particular, Tsallis entropy achieves no improvement in performance (see kappa and AUC values on Table 5) for Clonalg/CSCA and AIRS1 algorithms on Probing/R2L datasets. Although, it achieves best result when models are designed using U2R dataset and CLONALG algorithm.

For DoS, R2L and U2R attacks categories on the AIRS1 algorithm, the classification efficiency, in terms of kappa statistic and considering the selected attributes by the four attribute selection approaches, was significantly worse compared with the complete data set.

Based on Table 5, the preliminary results have pointed out that when an attribute selection scheme performed best in terms of a performance metric, this may not be true when other performance metric is used to evaluate the model. For example, using DoS dataset, Tsallis entropy performed best on AUC for any IAS algorithm and the ensemble approach performed best (excluding the complete attribute set) in terms of kappa performance metric when models are designed using AIRS1 algorithm.

Table 5. Experimental result for AIS algorithms Category Method 41 att Shannon Rényi Tsallis Ensemble kappa UAC kappa UAC kappa UAC kappa UAC kappa UAC DoS AIRS1 0.9745 0.959 0.9195 0.944 0.9209 0.868 0.9234 0.972 0.949 0.916 Clonalg 0.9929 0.9875 0.9943 0.995 0.9919 0.9904 0.9943 0.995 0.9916 0.9914 CSCA 0.9948 0.9935 0.9956 0.994 0.9946 0.993 0.9954 0.995 0.9948 0.9915 Probing AIRS1 0.9384 0.9775 0.9056 0.959 0.922 0.9655 0.9361 0.9735 0.9144 0.9795 Clonalg 0.9461 0.9855 0.9409 0.985 0.9344 0.9845 0.874 0.940 0.9388 0.9845 CSCA 0.9195 0.961 0.9138 0.952 0.9009 0.9485 0.883 0.9275 0.898 0.9455 R2L AIRS1 0.8885 0.9825 0.8612 0.949 0.8602 0.9495 0.3085 0.846 0.8735 0.9655 Clonalg 0.9116 0.9425 0.9119 0.942 0.9051 0.9425 0.9116 0.939 0.9121 0.945 CSCA 0.8755 0.9155 0.8829 0.928 0.8867 0.948 0.8744 0.9235 0.8833 0.9275 U2R AIRS1 0.7667 0.865 0.7331 0.9 0.7002 0.876 0.6741 0.9015 0.7338 0.961 Clonalg 0.7857 0.841 0.8699 0.9735 0.8789 0.962 0.8803 0.974 0.8699 0.9735 CSCA 0.7682 0.829 0.8547 0.962 0.8512 0.95 0.8285 0.9495 0.8699 0.9865

Another relevant result, when compared with Shannon entropy, is that using Tsallis entropy, it was achieved the same amount or even smaller set of attributes to detect attacks for all attacks categories and using Rényi entropy, it was achieved the same amount or smaller set of attributes for Probing, R2L and U2R attacks categories.

5. Conclusions

In this paper, it was presented an evaluation of Shannon, Rényi and Tsallis entropies and their applications in the area of intrusion detection system. Additionally, it was proposed an ensemble approach that combines the attributes selected by Rényi, Tsallis and Shannon information measures. In general, the experimental results have shown that selecting attributes based on Rényi, Tsallis entropies and ensemble approach achieve better results considering individual categories. Moreover, attribution selection approach based on Rényi or Tsallis entropies has reduced the amount of attributes and computational time. For future research, it will be used more detailed attributes from real network traffic that supposedly are able to better characterize packet contents as well as header data.

ACKNOWLEDGEMENTS

The authors would like to thank Brazilian Coordination for Improvement of Higher Education Personal (CAPES), National Council for Scientific and Technological Development (CNPq) and State Research Supporting Foundation of Maranhão (FAPEMA).