Payam Solatian , Seyed Hamidreza Abbasi , Fereidoon Shabaninia
School of Electrical and Computer EngineeringShiraz University,Iran
Correspondence to: Payam Solatian , School of Electrical and Computer EngineeringShiraz University,Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper deals with the basic concepts, mathematical parameters and design aspects of the Neuro-Fuzzy logic based controller for Non-Linear process plant to control flow rate of a system. Many techniques such as conventional PID and also fuzzy controllers have been proposed to control the flow rate. In this paper a new control approach is composed which is called PID ANFIS controller. Finally, the operation features of the three methods have been compared in terms of system overall performance. The designing of the scheme and the corresponding results have been tested by employing Matlab-Simulink. It will be shown that the composed ANFIS based controller is more versatile in comparison with those two others, for Non-Linear process plants. In addition, there is a considerable comparison between the three controllers in the presence of disturbance and environmental noise.
Keywords:
PID, Fuzzy Controllers, ANFIS, Non-Linear Process Control
1. Introduction
A novel scheme based on invoking of the fuzzy logic control concepts and ANFIS has been purposed in this paper to control a sample laboratory non-linear plant. The structure is shown in Figure 1.The process control consists of a reservoir tank that feeds water via a pressure–driven control valve and delay channel to a capacitance tank from the bottom of which the water flows through an orifice–type flow meter to a sump tank and then from this it is returned via a pump to the reservoir. These arrangements are illustrated in Figure 1and Figure 2 respectively.[1],[12]It is worth mentioning that in the considered process, the Outflow rate of the tank is to be maintained constant. In recent decades, PID controllers are always used by engineers to control such non-linear plants, but the tuning of parameters for traditional PID controllers was based on the mathematical model of the object, and some control rules, which was difficult to adapt. Moreover, the conventional PID controller has overshoots and settling time which are not desire items for investigators[1]. As time goes by, fuzzy control technology which was introduced by Zadeh in 1965 ,was applied to design a two-input and one-output self-adapting controller to control the flow rate of this laboratory process plant.,Figure 2.As it is extracted from the literature, the corresponding of the fuzzy controllers are better than the PID controllers, but it is not yet satisfies engineers and it is advised to be investigated by researcher to achieve better accuracies.[12]The three different controllers have been compared, being conducted firstly by using PID controller[1], secondly by employing fuzzy controller[12] and finally by using of composed method which is a special kind of ANFIS controller, called PID-ANFIS controller, to control the non-linear process plant. This composed method is a novel approach and as it is illustrated below, here, the inputs and outputs of the PID controller are to be applied to a Neuro-fuzzy system. For control purposes of the non-linear process plants, these three control approaches have been designed and the relative simulations were performed using Matlab package plus Simulink toolbox. Furthermore, environmental noises and disturbances are exerted to the controllers separately to exhibit the better performance of the composed method and it`s priority rather than those two other controllers.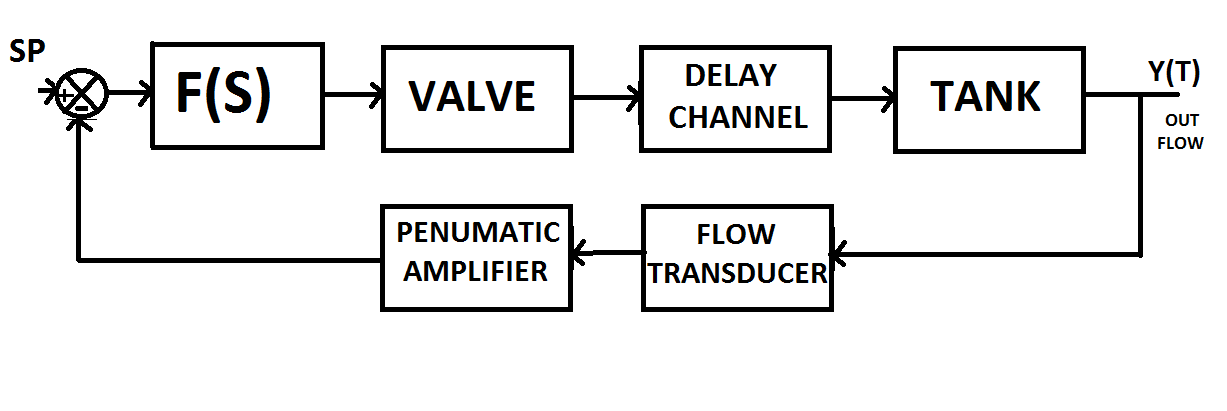 | Figure 1. System Block Diagram |
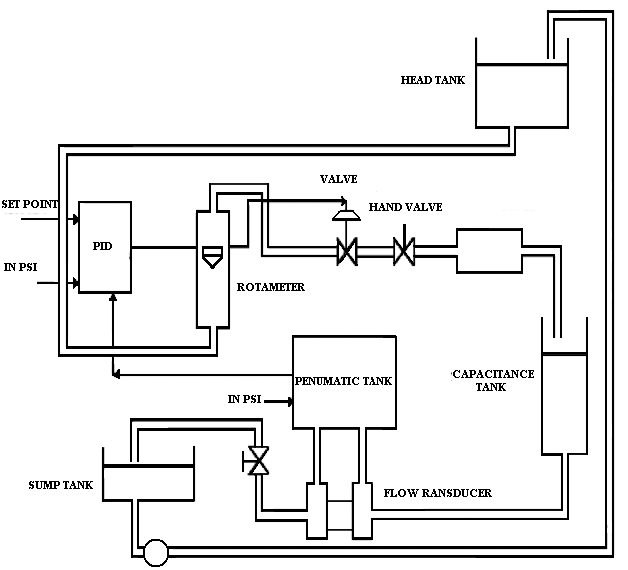 | Figure 2. System Schematic Arrangement |
1.1. Conventional Pid Controller Design
Proportional-integral-derivative (PID) controller may be the most widely used controller in the industries for the past two decades because of its simplicity and efficiency.The PID controller transfer function, F (s), is: F(s) = Kp(1+1/TiS+Tds)[1]Where: KP is the proportional gain of the Controller, KP / τi is the integral gain of the controller, Kp τd is the differential gain of the controller.How to appropriately tune the gains of PID controller is always an attractive problem. The attempts to obtain better performance and robustness by improving tuning formulae lead to several achievements, such as Ziegler-Nichols formula. All of the tuning formulas need to know critical gain and critical period for tuning. If we don’t have the prior knowledge of the system dynamics, the auto tuning method would be a solution.[4]
1.1.1. Ziegler-Nichols Tuning
Ziegler and Nichols, both employees of TaylorInstruments, described simple mathematical procedures, the first and second methods respectively, for tuning PID controllers. These procedures are now accepted as standard in control systems practice. Both techniques make a priori assumptions on the system model, but do not require that these models be specifically known. Ziegler-Nichols formula for specifying the controllers are based on plant step responses.[4]
1.1.2. The First Method
The first method is applied to plants with step responses of the form displayed in Figure 3. This type of response is typical of a first order system with transportation delay, such as that induced by fluid flow from a tank along a pipe line. It is also typical of a plant made up of a series of first order systems. The response is characterized by two parameters, L the delay time and T the time constant. These are found by drawing a tangent to the step response at its point of inflection and noting its intersections with the time axis and the steady state value. The plant model is therefore G(s) = 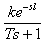 , Ziegler and Nichols derived the following control parameters based on this model which is describes in table1:
, Ziegler and Nichols derived the following control parameters based on this model which is describes in table1:| Table 1. Ziegler-Nichols Recipe – First Method |
| | PID Type | Kp | Ti=Kp/Ki | Td=Kd/Kp | | P | T/L | ∞ | 0 | | PI | 0.9(T/L) | L/0.3 | 0 | | PID | 1.2(T/L) | 2L | 0.5L |
|
|
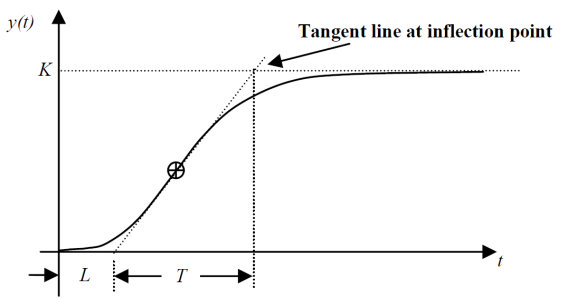 | Figure 3. Response Curve for Ziegler-Nichols First Method |
1.1.3. The Second Method
The second method targets plants that can be rendered unstable under proportional control. The technique is designed to result in a closed loop system with 25% overshoot. This is rarely achieved as Ziegler and Nichols determined the adjustments based on a specific plant model.The steps for tuning a PID controller via the 2nd method are as follows:Using only proportional feedback control:1. Reduce the integrator and derivative gains to 0.2. Increase Kp from 0 to some critical value Kp=Kcr at which sustained oscillations occur. If it does not occur then another method has to be applied.3. Note the value Kcr and the corresponding period of sustained oscillation, PcrThe controller gains are now specified as follows in table2:| Table 2. Ziegler Nichols Recipe – Second Method |
| | PID Type | Kp | Ti=Kp/Ki | Td=Kd/Kp | | P | 0.5 Kcr | ∞ | 0 | | PI | 0.45 Kcr | Pcr/(1.2) | 0 | | PID | 0.6 Kcr | Pcr/2 | Pcr/8 |
|
|
1.2. Fuzzy Controller Design and the Fuzzy Linguistic Control
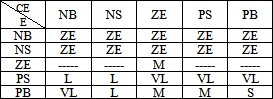
Fuzzy sets are a generalization of conventional set theory that were introduced by Zadeh in 1965 as a mathematical way to represent vagueness in everyday life[1]. The basic idea of fuzzy sets is easy to grasp. Suppose, as you approach a red light, you must advise a driving student when to apply the brakes. Would you say, "Begin braking 4 feet from the crosswalk"? Or would your advice be more like, "Apply the brakes pretty soon"? The latter, of course; the former instruction is too precise to be implemented. This illustrates that precision may be quite useless, while vague directions can be interpreted and acted upon. Everyday language is one example of ways vagueness is used and propagated. Automatic Control theory has developed in the last decades from an empirically oriented technique into a strongly mathematically based technique, requiring precision, well defined concepts and exact data. Nevertheless vagueness and subjectivity still play a role as is pointed out further on. Thus, notwithstanding the creation of numerous mathematical control techniques, the final decision about the 'goodness' of a system's behaviour remains a personal, subjective task. Under the surface of modern control techniques subjectively, vagueness-- unconsciously- still does play a role. Furthermore, in non-engineering systems, the co-called 'soft systems', subjective matters are almost always predominant. A theory of vagueness could be very useful here. Complex industrial plants such as chemical reaction processes or controlling the flow of a system such as this paper often are difficult to control automatically. In some cases Non Linear plant models can be derived from the underlying physical or chemical properties of the process. Usually this requires very elaborate calculations. Even under various approximations, the final model is difficult, of high order, nonlinear, time varying etc. Parameter estimation methods to obtain a purely mathematically described behavioristic model may also be complex, time consuming and therefore costly. When nonlinearity, time variance and stochastic disturbances are important, modeling methods become still more complicated..[2][7][6]On the other side it is interesting to note that in many cases the control of a process by a human operator is more successful than any such automatic control. Hence it seems worthwhile to investigate the control policy of the operator. In industrial process plant it was difficult to control because of nonlinearity and variability with conventional PID controller. Nowadays it can be control by a fuzzy algorithm based on the experience of a human operator.From a set of linguistic rules which describes the operator's control strategy a control algorithm is constructed where fuzzy sets define the words used. Several types of such an algorithm are implemented and compared in behaviour as well as in structure. An alternative algorithm--mathematically equivalent to the other--is proposed to speed up the computation.. Fuzzy controller includes the fuzzification, knowledge base, inference engine and de fuzzification. Fuzzy controller makes the input accurate quantity to fuzzy quantity. It maps the input to the corresponding discourse. The knowledge base contains the experienced knowledge of the flow process station. Data base contains the membership function of every linguistic variable. Control rules are described by the data base. Defuzzification again transforms the fuzzy quantity into accurate quantity. To introduce qualitative selection requirements in weighted Boolean systems, the numeric weights can be replaced by linguistic descriptors of the desired documents. Thus, linguistic descriptors play the role of fuzzy specifications of ideal index term weights. They are used to fuzzify numeric weights; in fact, weights such as 0.85, 0.86, and 0.9 are so close to each other that they could equally indicate that the term is very important in the desired documents. Linguistic descriptors, such as very important, fairly important, or not very important can be used to fuzzify weights interpreted as ideal index term weights.[3]In the same way, other linguistic descriptors could be defined to fuzzify query term weight semantics, such as a threshold or relative semantics.[8]At this stage, other levels of fuzziness, such as the use of quantification descriptors or the fuzzification of the AND and OR operators, are not formalized. Thus by defining the appropriate fuzzy sets and translating the rules as fuzzy implications of the form: if A then B, as functions of those fuzzy sets (A and B), the human control strategy can be converted into a control algorithm and implemented on a computer as outlined below. This paper also uses a form of system having two inputs and one output. The inputs are also the flow rate error and the derivative flow rate of error and the output is the flow rate. In order to obtain one deterministic output value from this fuzzy output set a decision procedure has to be adopted to make a choice as to which particular value is a good representative of the fuzzy set. The simple decision procedure applied here is to take that output value at which the membership function is maximal.The table 3 shows the membership functions where:Table 3. Membership Functions of Fuzzy Controller
 |
| |
|
It should be noted that the membership functions for the two inputs are: {NB,NS,ZE,PS,PB} and also the membership functions for the only flow output is : {ZE,S,M,L,VL} this is because the input of the valve(also the output of the controller) in this paper is[0 1] .Figure 4 shows the surface view of the fuzzy controller when membership functions of table3 is exerted.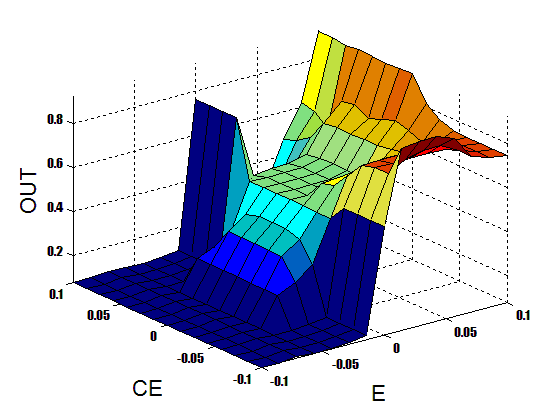 | Figure 4. Surface View Of Fuzzy Controller |
1.3. Adaptive Neuro-Fuzzy Inference System (Anfis)
ANFIS is the implementation of fuzzy inference system (FIS) to adaptive networks for developing fuzzy rules with suitable membership functions to have required inputs and outputs. FIS is a popular and cardinal computing tool to which fuzzy if-then rules and fuzzy reasoning compose bases that performs mapping from a given input knowledge to desired output using fuzzy theory. This popular fuzzy set theory based tool have been successfully applied to many military and civilian areas of including decision analysis, forecasting, pattern recognition, system control, inventory management, logistic systems, operations management and so on. FIS basically consist of five subcomponents, a rule base (covers fuzzy rules), a database (portrays the membership functions of the selected fuzzy rules in the rule base), a decision making unit (performs inference on selected fuzzy rules), fuzzification inference and defuzzification inference. The first two subcomponents generally referred knowledge base and the last three are referred to as reasoning mechanism (which derives the output or conclusion). An adaptive network is a feed-forward multi-layer Artificial Neural Network (ANN) with; partially or completely, adaptive nodes in which the outputs are predicated on the parameters of the adaptive nodes and the adjustment of parameters due to error term is specified by the learning rules. Generally learning type in adaptive ANFIS is hybrid learning. General structure of the ANFIS is illustrated in Figure 5.[11],[9]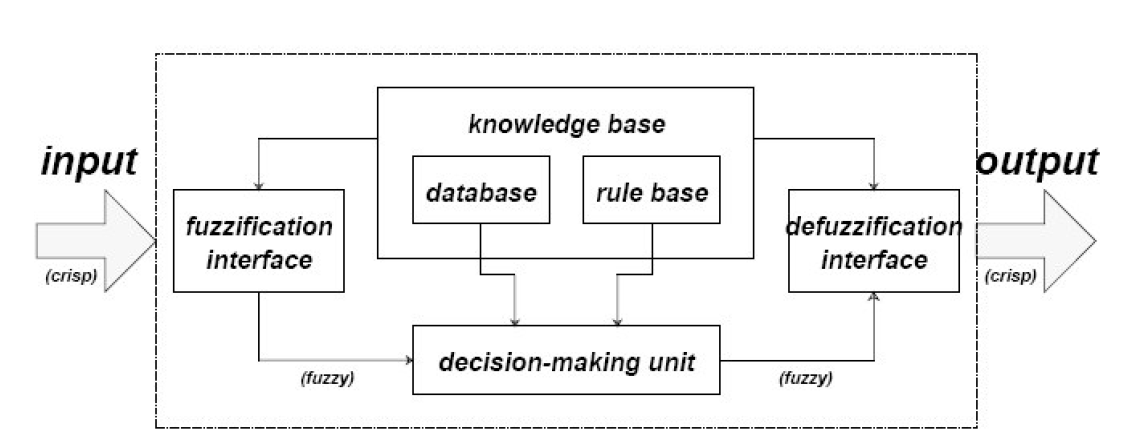 | Figure 5. ANFIS Structure |
2. Composed Method
As it was mentioned, for good performance of An ANFIS controller, it should be fed by optimized inputs and outputs. In order to achieve this goal, many methods have been invented. This paper tries to create a new method of feeding the inputs and output of an ANFIS which is here called PID-based ANFIS method in 5 steps: 1st: In the first step of this method we assume a special transfer function and control it with a PID controller with the best P, I & D parameters.This controller should control that process well with best P I & D parameters. 2nd: At this stage of this method ,the output of the PID controller should be sent to the workspace in MATLAB software in some points.Its better to have some more points to have better accuracy. 3rd: At this step, these points should be modified and optimized the points by an expert operator, on the points that the PID controller does not act well. 4th: During this step of this method after modification the points, we train the ANFIS inputs and output with these modified points.The inputs are the error and the deviation of the error ,and the output is the output of 3rd step. 5th: In this step we use this new ANFIS controller to control the mentioned transfer function.After above steps the ANFIS controller has some Fuzzy rules and memberships with special inputs and output. This may used also for unknown Non-Linear process plants. In the first step ,In order to achieve this goal we can control the process with a PID controller. After that with the composed method we can have the ANFIS controller to control that unknown process much better. In addition, by utilizing that way if we have an unknown controller which is now controls a system, we can find an ANFIS controller to use instead of that unknown controller and control that system with known control parameters.Figure 6 shows the surface view of the composed controller when membership functions of ANFIS controller are exerted.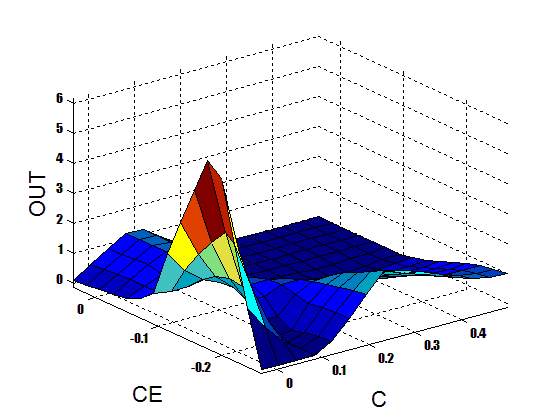 | Figure 6. Surface View of Composed Method |
3. Simulation study(results and design)
3.1. Simulation Results with No disturbancea and Noise
| Table 4. Comparison Table |
| | Specification | PIDController | FuzzyController | ANFISMethod | | Rise Time | 4.5 sec | 4 sec | 2.5sec | | Peak Overshoot | 0.04 | 0.02 | 0 | | Settling Time | 10 sec | 8 sec | 6sec |
|
|
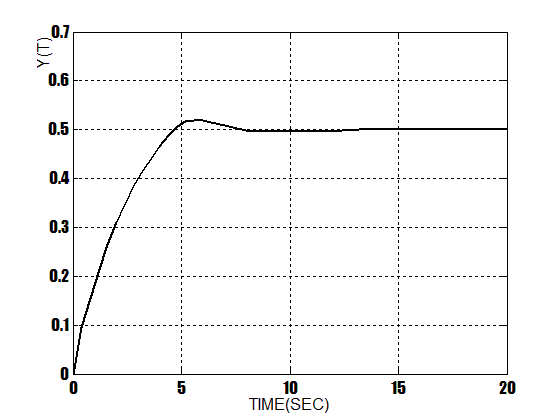
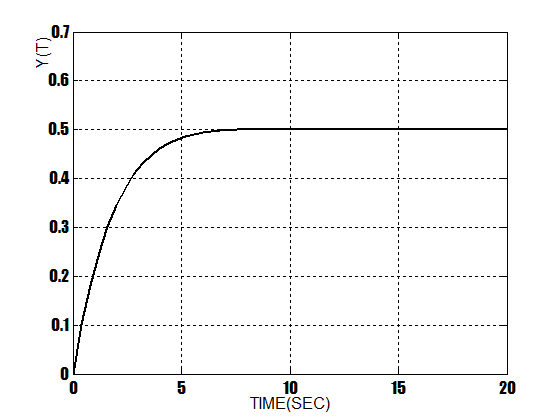
This paper analyses the three models of controllers to control the output flow of the schematic shown in Figure 2. The simulations indicate that the PID based ANFIS designed controller is much more versatile compared with the conventional PID and the fuzzy controller for Non-Linear process plants. Figure 7 illustrates the output of the system with conventional controller. Figure 8 indicates the output with fuzzy controller, and also in Figure 9 you can see the output of the system when ANFIS controller uses. Test results can be verified that with using this model of PID based ANFIS controller Non-Linear process plant can be controlled ,and also has better response to an 0.5u(t) input. In Table4 the results of these three methods are compared, with their Rise time, Settling time and also Peak Overshoot. 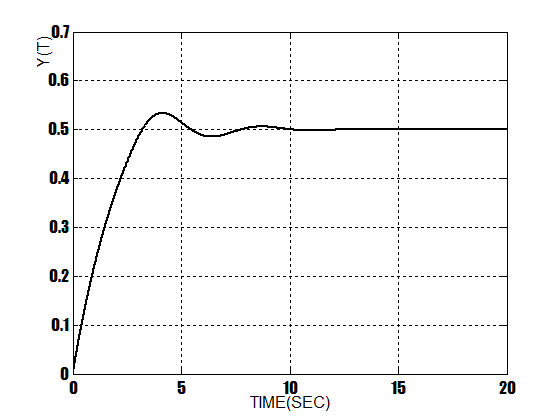 | Figure 7. Response Of PID Controller At 0.5u(t) Input |
 | Figure 8. Response Of Fuzzy Controller At 0.5u(t) Input |
 | Figure 9. Response of Composed Controller At 0.5u(t) Input |
3.2. Simulation Results with Noise
At this stage a Gaussian noise is exerted to the input of the system .Figure 10 shows this Gaussian noise block diagram in which create a noise between seconds 5 to 8. Figure 11 shows the response of PID controller when a Gaussian noise is exerted. Also Figure 12 shows the response of the fuzzy controller when a Gaussian noise is exerted and at last Figure13 shows the response of this composed method when noise is exerted. As it can be seen, there are some differences between the outputs of three controllers in following with its input. In mentioned figures, responses are in black, also the noise is in blue. As the simulation indicates, the composed method has better response in following its input,it has no overshoot and much more versatile to ignore the noise and follow the setpoint. 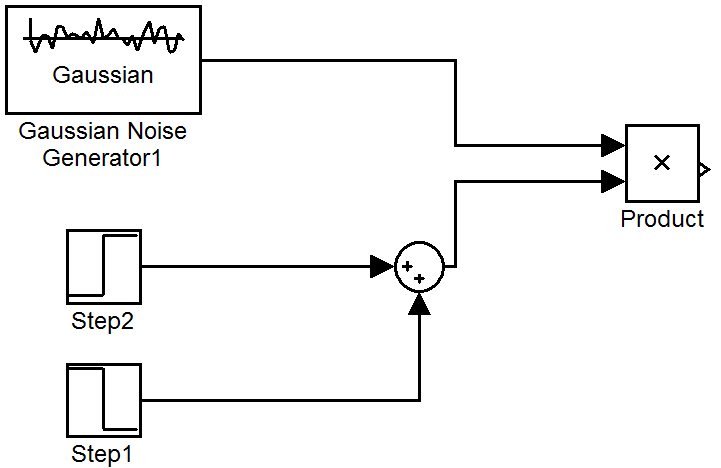 | Figure 10. Gaussian noise |
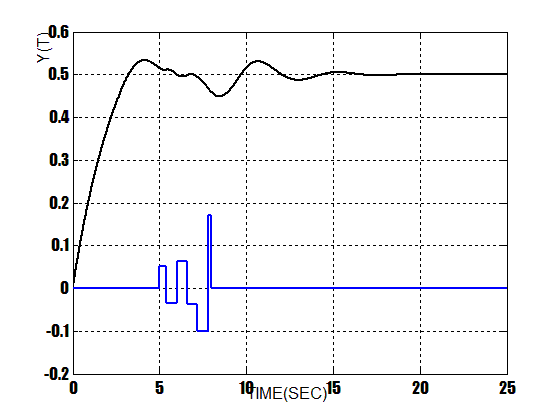 | Figure 11. Response Of PID Controller With Noise |
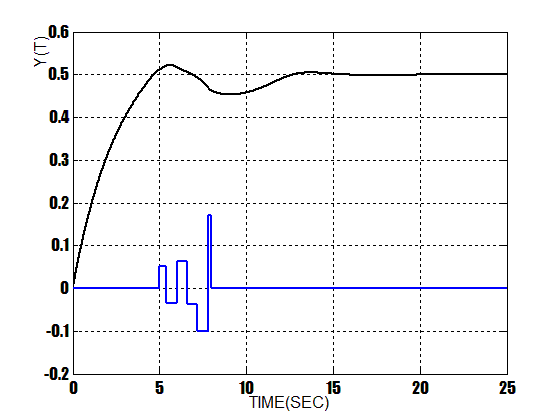 | Figure 12. Response Of Fuzzy Controller With Noise |
3.3. Simulation Results with Disturbance
At this stage a disturbance is exerted to the output of the system . Figure 14 shows this disturbance block diagram. Figure 15 shows the response of PID controller when a disturbance is exerted also, Figure 16 shows the response of fuzzy controller when a disturbance is exerted and finally Figure 17 shows the response of composed controller when a disturbance is exerted. As it can be seen, there are some differences between the responses of three controllers in following its input. In mentioned figures, responses are in black, also the disturbance is in blue. As the simulations indicate, the composed method has better response in following its input ,it has no overshoot and much more versatile to ignore the noisedisturbance and follow the setpoint. 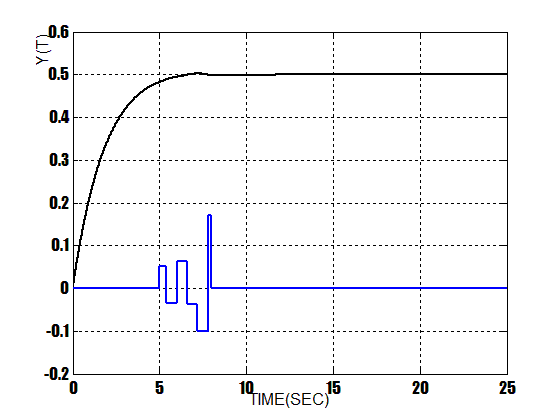 | Figure 13. Response Of Composed Controller With Noise |
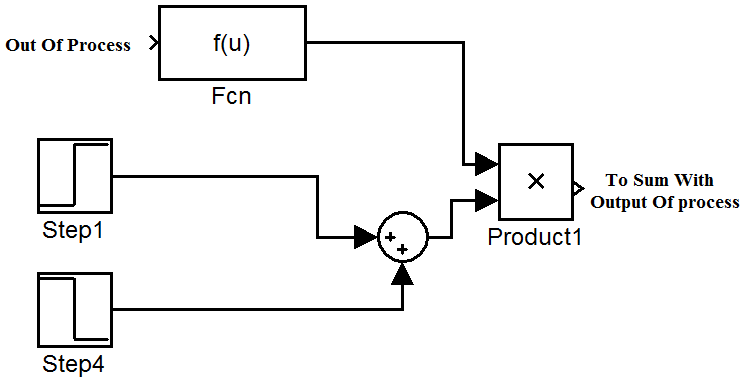 | Figure 14. Disturbance |
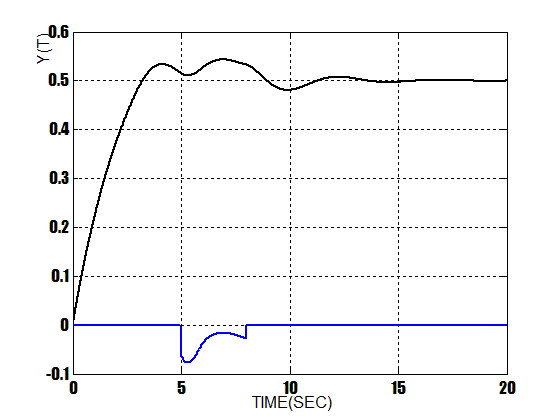 | Figure 15. Response Of PID Controller With Disturbance |
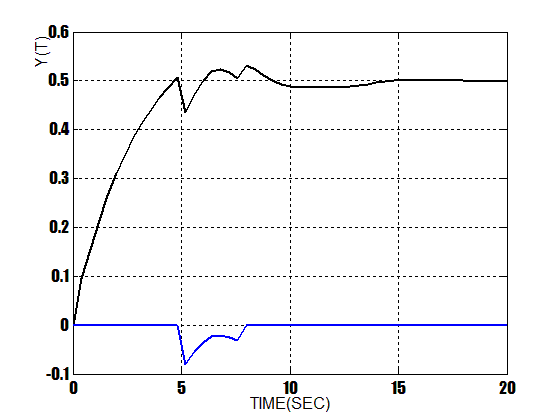 | Figure 16. Response Of Fuzzy Controller With Disturbance |
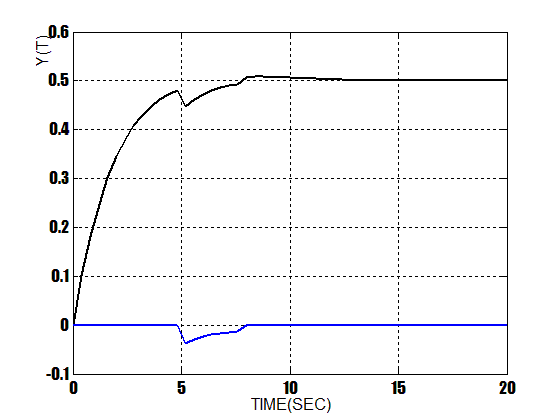 | Figure 17. Response Of Composed Controller With Disturbance |
4. Conclusions
As it is mentioned and due to the simulation results, this promoted ANFIS called PID-ANFIS has the membership functions and also rules. As results reveal, this composed method has better response in following its input with no overshoots and also has settling time less than the other ways of control. An advantage of this method is the usage of it , for controlling an unknown ,Non-Linear, process plant.By this way that unknown process can be controlled with a PID controller, after that we took the input and output of the controller and exert them to this composed method.Now there is a PID-ANFIS controller that can control that unknown process. Also, when a system has an unknown controller, that its not possible to access the parameters of that controller, by using this method inputs and output of that unknown controller are given, and are exerted to that ANFIS controller. Now known rules and membership functions can be created, and change to have better control, and also have same informations about that unknown controller. The results of the output with any of the controllers can be seen in simulation results. If the results of the simulations with noise and disturbance are compared, it will be shown that the ANFIS composed controller has better response in following its input,even when noise and disturbance are exerted.
References
| [1] | H.H.Tahir,A.Al-Rawi Mechatronics department,control mechatronics research center:.Variable structure control design of process plant based on sliding mode approach . |
| [2] | L.A.Zadeh: Fuzzy Sets: Information and Control,8,338- 353(1965) |
| [3] | Gloria Bordogna and Gabriella Pasi, JOURNAL OF THE AMERICAN SOCIETY FOR INFORMATION SCIENCE - March 1993 |
| [4] | J. G. Ziegler and N.B.Nichols:“Optimum Settings for Automatic Controllers”, Trans. of ASME, Vol. 64, Ch. 4 , PP. 759 – 768, 1942. |
| [5] | Vue Wei-jie, Liu Yong-xin (2009), “Boiler drum Level controlled by Fuzzy Self- adapting PID”, second Asia-Pacific Conference on Computational. intelligence and Industrial Applications. |
| [6] | Chen, G., Pham, T.T. (2001). Introduction to Fuzzy Sets, Fuzzy Logic, and Fuzzy Control Systems. CRC Press, New York. |
| [7] | Cox, E. (1994). The Fuzzy Systems Handbook: A Practitioner’s Guide to Building, Using, and Maintaining Fuzzy Systems. Academic Press, New York. |
| [8] | Driankov, D., Palm, R. (1998). Advances in Fuzzy Control. Physica–Verlag Heidelberg, New York. |
| [9] | Lin, C. T. : Neural Fuzzy Control Systems with Structure and Parameter Learning, World Scientific, NY, 1994. |
| [10] | Zilka, V.—HAL´AS, M.—Huba, M. : Nonlinear Controllers for a Fluid Tank System, Lecture Notes in Computer Science Vol. 5717, Computer Aided Systems Theory EUROCAST 2009, Springer-Verlag, Berlin Heidelberg, 2009, pp. 618-625. |
| [11] | Shi, Y.—Muzimoto, M. : Some Considerations on Convention Neuro-Fuzzy Learning Algorithms Gradient Descent Method, Fuzzy Sets and Systems 112 (2000), 51 63. |
| [12] | R.Manoj Manjunath S.Janaki Raman:Fuzzy adaptive PID for flow control system based on OPC-IJCA Special issue on computer science new dimensions & perspectives NCCSE 2011. |



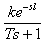 , Ziegler and Nichols derived the following control parameters based on this model which is describes in table1:
, Ziegler and Nichols derived the following control parameters based on this model which is describes in table1:














 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML