-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Intelligent Systems
p-ISSN: 2165-8978 e-ISSN: 2165-8994
2012; 2(5): 82-92
doi:10.5923/j.ajis.20120205.02
Performance Evaluation and Optimisation of Industrial System in a Dynamic Maintenance
Smaïl Adjerid, Toufik Aggab, Djamel Benazzouz
Solid Mechanics and Systems Laboratory (LMSS), M’Hamed Bougara University (UMBB), Boumerdes 35000, Algeria
Correspondence to: Smaïl Adjerid, Solid Mechanics and Systems Laboratory (LMSS), M’Hamed Bougara University (UMBB), Boumerdes 35000, Algeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Despite the existence of the multitude of behavioral analysis tools for industrial systems, increasingly complex, managers to date find difficulties to define maintenance strategies able to significantly improve the overall performance of companies in terms of production, quality, safety and environment. A static maintenance and not adapted to the evolution of the state system does not meet the expectations of industrialists. However, the behavior of any degradable system is closely related to the state of its components. This random influence is not always sufficiently considered for various reasons, consequently any decision making remains subjective. Our approach based on dynamic Bayesian networks (DBN) consists has the modeling of the system and the functional dependencies of its components. The results obtained then, after the introduction in the model of the most appropriate actions of maintenance show all the importance of this technique and the possible applications.
Keywords: Performance Evaluation, Reliability, Dynamic Maintenance Strategy, Bayesian Network
Cite this paper: Smaïl Adjerid, Toufik Aggab, Djamel Benazzouz, Performance Evaluation and Optimisation of Industrial System in a Dynamic Maintenance, American Journal of Intelligent Systems, Vol. 2 No. 5, 2012, pp. 82-92. doi: 10.5923/j.ajis.20120205.02.
Article Outline
1. Introduction
- The functioning reliability evaluation of an industrial system in operating mode consists of analyzing failures component to estimate their impact on the service provided by the system [1], [2] and [3].A particularity in characterizing a number of industrial systems is that their behavior varies as function of time due to interactions between components of the system or as function of the environment. Thus, we are talking about dynamic reliability [4], [5], which render conventional methods of functioning reliability static and ineffective. According to [6] the dynamic reliability is the predictive evaluation reliability of a system, whose reliability structure expresses how the system failure depends on the failures of its components, evolves dynamically over time.Thus, an industrial system will evolve physically over time in nominal operation, in a degraded or failed mode. The maintenance and the process organization which allow the functioning of a system will have an impact on its performance.In general, the efficiency evaluation of the maintenance action can be done by estimated methods based on feedback experience knowledge or Bayesian methods based on expert opinions [7], [8].Bayesian networks (BN) are based on graph theory and probability theory. They allow to represent intuitively systems whose state evolves in a non- deterministic manner [9]. In addition, they have the ability to integrate in the same model various kinds of knowledge (Rex, expertise and observation).However, the BN formalism does not allow to represent systems evolving over time i.e that contain variables whose conditional probability table (CPT) in present time which depends on past information [10], [11]. This problematic type led us to use dynamic Bayesian networks (DBN). The DBN are an extension of BN which model a stochastic processes varying over time. In addition statistical nodes used in conventional BN, DBN introduce a new type of nodes called temporal nodes to model discrete random variables depending on time [12], [13] and [14].The objective of this paper is to evaluate the system reliability without maintenance intervention, then show what will be the efficiency of the maintenance strategy of the same system.The performance evaluation model for a maintained system involves the following steps:- modeling the system from its topo-functional decomposition in components,- modeling the degradation modes of various components,- modeling functional dependencies between components and their effects on the process of the system by measuring the safety parameter,- identification and incorporation of maintenance strategies and system performance evaluation.
2. Bayesian Approach for a Degradable System
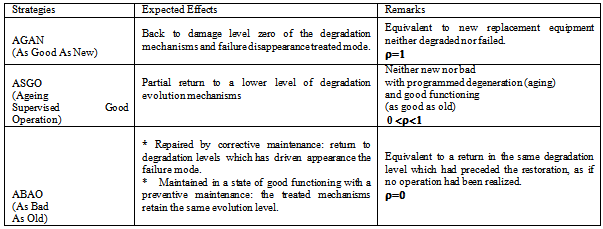
- The degradation of a system can be considered according to various modes. It is suggested to consider them according to the following two situations: the system is not maintained (only a few corrective maintenance operations are realised) or the system is maintained according to predefined maintenance strategy.The topology describing the degradation of a component is shown in Figure 1 [9], [10], [15], [16].
 | Figure 1. Topology Describing Degradation Component |
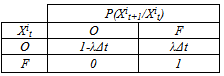
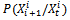 allocating the probability to see the component (system) changing from state
allocating the probability to see the component (system) changing from state 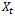 to state
to state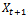 . In this phase, two groups of components are to be distinguished: the components at constant failure rate, and those with variable failure rate:• Components at constant failure rate:The set values of variable is val
. In this phase, two groups of components are to be distinguished: the components at constant failure rate, and those with variable failure rate:• Components at constant failure rate:The set values of variable is val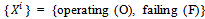 , in this case we should determine only the conditional probabilities:
, in this case we should determine only the conditional probabilities: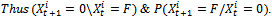
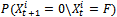 indicates the probability that the component passes naturally from the failure state to the operating state for non-auto repairable systems. It is equal to zero.
indicates the probability that the component passes naturally from the failure state to the operating state for non-auto repairable systems. It is equal to zero.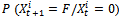 indicates the probability that the component state degrades over time period Δt separating the decision instants t & t+1. This means that,
indicates the probability that the component state degrades over time period Δt separating the decision instants t & t+1. This means that,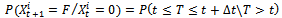 | (1) |
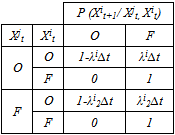
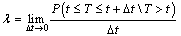 | (2) |
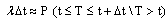 | (3) |
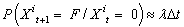 | (4) |
|
 | (5) |
|
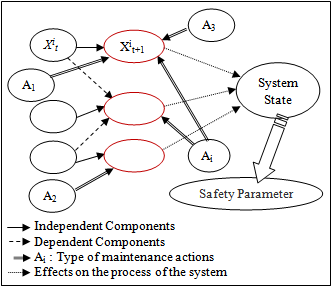 | Figure 3. General Layout of the Model |
3. Industrial System Description
- Analysis of real case study with and without maintenance described above was applied to a Blower of a lemonade production line.Figure 4 shows the production line of soft drink for formats 0.5l or 2l depending on the configuration of the machines. At the input line, there are the raw materials appearing in preform and at the output line we get packaged bottles on pallets to be transferred to the stock.The blowing process consists of the following phases:• a heated preform is placed in the open blow mold,• the blowing mold closes, the elongation rod move gradually, first in the transport chuck then, when the blowing mold is locked, into the preform up to its ends,• the joining piston connects tightly to the chuck transport,• when the elongation rod reaches the end of the preform, blowing air P1 is switched ON through a high-flow valve. A limited supply of P1 allows to control the formation of the "bubble bottle" and thus a homogeneous distribution of the material,• the blowing pressure P1 is deactivated and the blowing pressure P2 is activated, the bubble bottle is pressed onto the mold wall with a higher pressure. This system allows the finest contouring of the bottle,• the blowing process is complete when the blowing air P2 is cute through the high-flow valve P2 and when the blowing air is discharged through the piston and the high flow valve in the silencer,• the connecting piston is downed, the blowing mold is unlocked and opened, and the finished bottle is extracted from the opened blowing mold.In this production line, the Blower is taken as a case study because of the following reasons:• the high frequency of failure of this machine,• the technology complexity of the machine,• the machine maintenability.
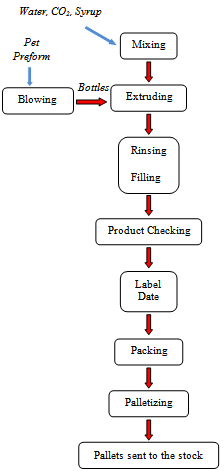 | Figure 4. Production Line of Soft Drink Manufacturing Process |
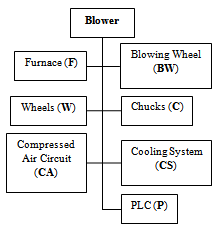 | Figure 5. Blower Decomposition |
4. Modeling and Simulation of a System Functioning Mode
4.1. Behavioral analysis of system components
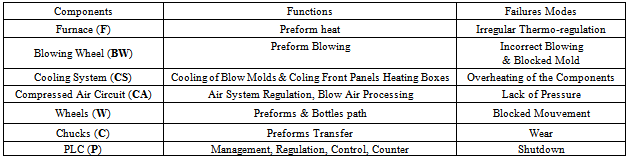
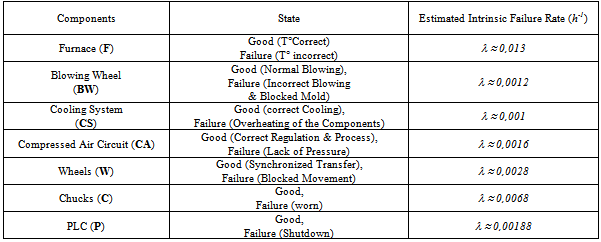
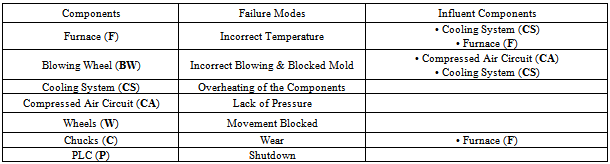
- To simplify the analysis of the components behaviour, in the first step are analyzed separately and then treated according to their mutual dependencies, given that initially the system is not maintained.For each component the function and the failure mode are defined as shown in Table 3.
|
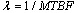 | (6) |
|
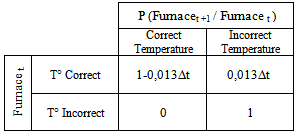
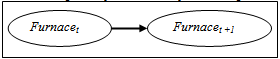 | Figure 6. Degradation Indication Topology of the Furnace |
|
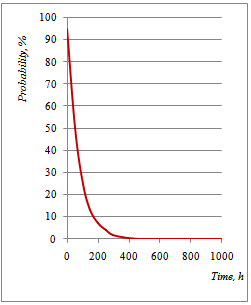 | Figure 7. Dynamic Evolution Probability of the Furnace Good Functioning |
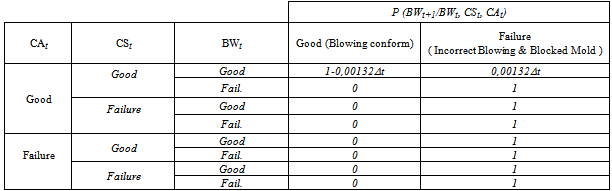
|
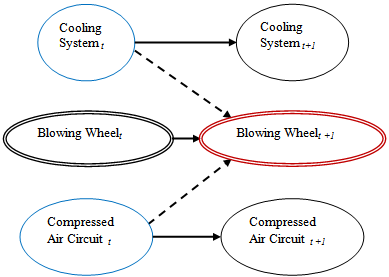 | Figure 8. Topology Indicating the Blowing Wheel Degradation with its Functional Dependencies |
|
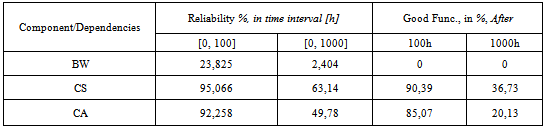
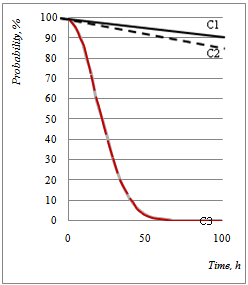 | Figure 9. Evolution of the Dynamic Probability in Good operation of the Blowing Wheel and its two dependencies in [0,100h] interval |
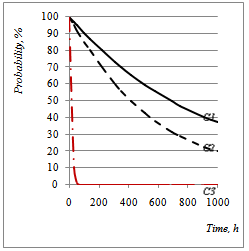 | Figure 10. Evolution of the Dynamic Probability in Good operation of the Blowing Wheel and its two dependencies in [0,1000h] interval |
|
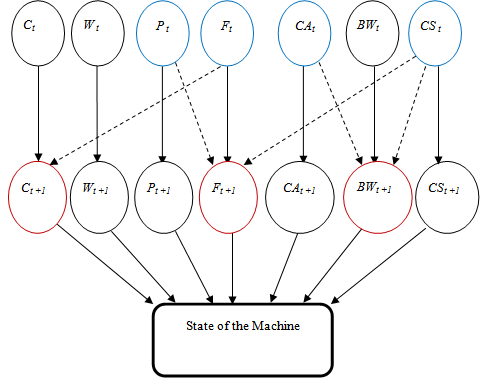 | Figure 11. Proposed Model Topology |
4.2. Network Architecture Conception
- The equivalent network architecture was developed under Netica software, before taking into account maintenance strategies.Each input node indicates a machine component.The solid lines are synchronous arcs, and they represent the relationship between components and machine state.
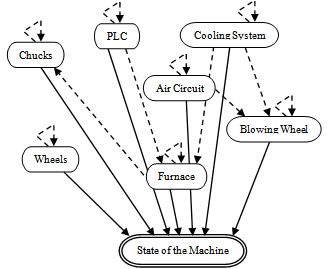 | Figure 12. Proposed Model without Maintenance |
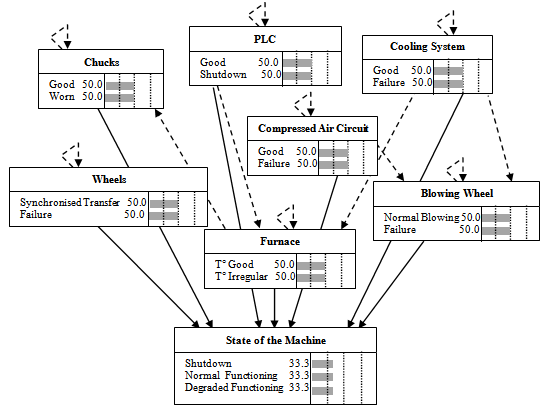 | Figure 13. Global Modes Network |
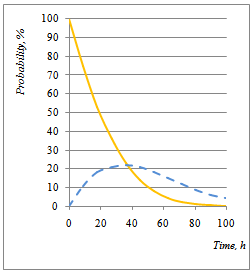 | Figure 14. The Dynamic Probability Evolution of Good Functioning of the Blower and Scrap Rate |
|
|
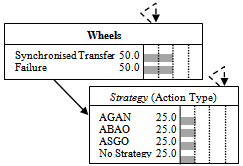 | Figure 15. State Evolution Model of Wheels Taking Into Account its Associated Maintenance Action |
| |||||||||||||||||||||||||||||||||||||
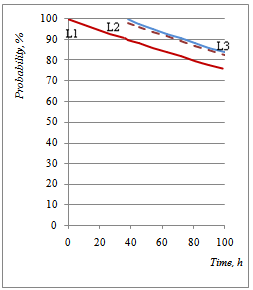 | Figure 16. Dynamic Probability Evolution of Wheels in Good Functioning Mode Based on Possible Strategy of Maintenance |
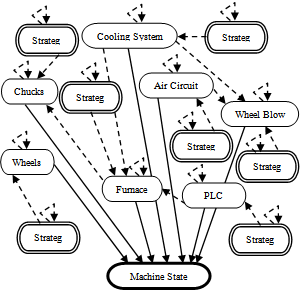 | Figure 17. Global Model Architecture |
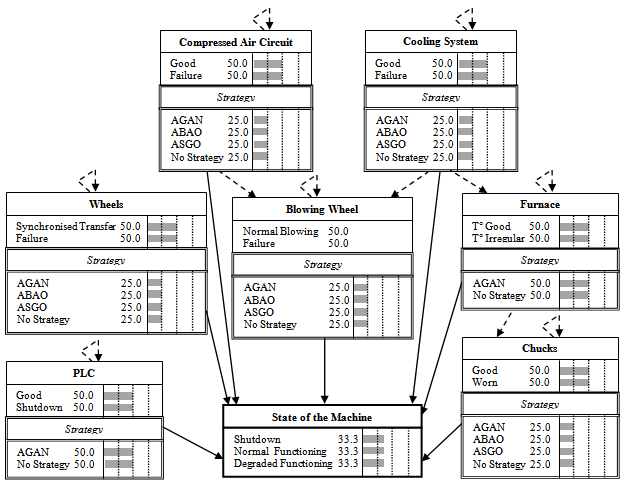 | Figure 18. Topology Representing the Nodes of the Global Model |
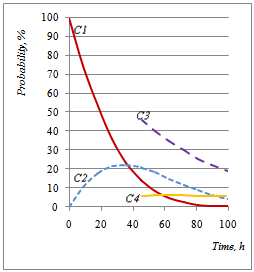 | Figure 19. Dynamic Probability Evolution of the Blower Good Functioning with the Applied Strategy |
4.3. Application
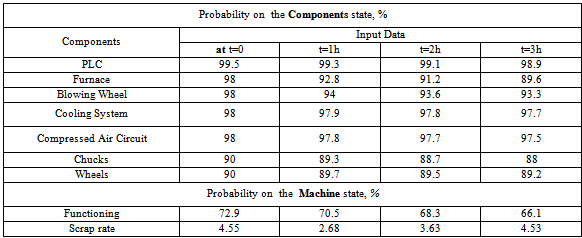
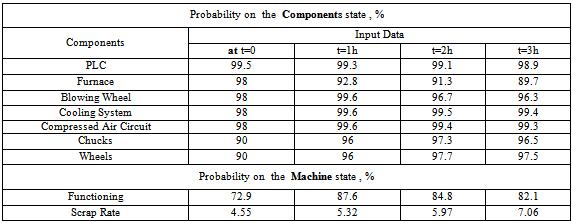
- The performed simulations with this network, without any architecture modification and conditional probabilities tables, in various scenarios (diagnosis, predictions and combined reasoning) allows to show the efficiency and flexibility of this tool as a decision tool.If, wish for example, to establish a prediction of the maintenance strategy impact, simply insert the input nodes values of the components according to their estimated state at instant t and the appropriate maintenance strategy. Informed input nodes automatically update output nodes from t to t+n.The approach consists in comparing the state evolution of the machine with and without maintenance strategy.If no maintenance action is considered (strategy = 0) and considering the components at t = 0 are in good state, thus the obtained results are given in Table 13.
|
|
5. Conclusions
- In this paper, a model is developed for a system behavioral analysis by considering the degradation modes of various components some of which may be interrelated and have variable behaviours and unwanted, influencing later on the physical evolution of the entire system. Then in the final architecture of the model were incorporated types of maintenance strategies and their reciprocity efficiency.The attempts in the design of the model we have taken to the ration of a flexible architecture for its various applications and easy to implement.Throughout the presented example, we illustrate the approach usefulness and its use as part of a process for predictive evaluation of the safety parameters of a system in operating modes and the effects of maintenance strategies. The network learning was realized by exploiting the data obtained from various sources (expert opinions, historical).Other possible use is that the model can serve to plan the actions of maintenance by giving the periods and the natures of the intervention of a way anticipated according to the constraints in terms of objectives of performance. That is be able to envisage in a simultaneous way the nature of the action as well as its moment of execution. In that case, the strategies of maintenance will thus be designed by a set of couples (time, action), what constitutes a tool of reliable decision for the managers of maintenance. This aspect we continue to develop it by including other variables such as the costs associated to each strategy of maintenance, the protocols of the interventions etc…
ACKNOWLEDGEMENTS
- The author would like to thank Prof. Ahcene SERIDI for reviewing the final manuscript.
References
| [1] | N. Sadou, "Aide à la conception des systèmes embarqués sûrs de fonctionnement", Doctoral dissertation, University of Toulouse, France, 2007. |
| [2] | A. Demri, "Contribution à l’évaluation de la fiabilité d’un système mécatronique par modélisation fonctionnelle et dysfonctionnelle", Doctoral dissertation, University of Angers, France, 2009. |
| [3] | Philippe Weber, Gabriela Medina-Oliva, Christophe Simon, Benoît Iung, "Overview on Bayesian networks applications for dependability, risk analysis and maintenance areas", Engineering Applications of Artificial Intelligence, Vol. 25, no. 4, June 2012, pp. 671-682, 2010. |
| [4] | Smidts Carol-Sophie, Devooght Jacques, Labeau Pierre-Etienne, "Theoretical basis of dynamic reliability problems", in Proceedings of the 4th Workshop on Dynamic Reliability, pp.11-44. International Workshop Series on Advanced Topics in Reliability and Risk Analysis, Center for Reliability Engineering, University of Maryland, College Park, USA, 2000. |
| [5] | R. Schoenig "Définition d’une méthodologie de conception des systèmes mécatroniques sûrs de fonctionnement", Doctoral dissertation, National polytechnic institute of Lorraine, France, 2004. |
| [6] | P. Casandeas, "Evaluation par simulation de la sûreté de fonctionnement de systèmes en contexte dynamique hybride", Doctoral dissertation, University of Nancy, France, 2009. |
| [7] | L. Doyen, O. Gaudoin,"Modélisation de l'efficacité de la maintenance des systèmes réparables - Synthèse bibliographique", Contract Report T50L47/F00555/0 between EDF and LMC, National polytechnic institute of Grenoble, Fraance, 2004. |
| [8] | Gilles Celeux, Franck Corset, Andre Lannoy, B Ricard, "Designing a Bayesian Network for Preventive Maintenance from Expert Opinions in a Rapid and Reliable Way", Reliability Engineering and System Safety, Vol. 91, no. 7, pp. 849-856, 2006. |
| [9] | Roland Donat, "Modélisation de la fiabilité et de la maintenance par modèles graphiques probabilistes. Application à la prévention des ruptures de rails", Doctoral dissertation, Applied Sciences National Institute of Rouen, France, 2009. |
| [10] | Laurent Bouillaut, Roland Donat, Patrice Aknin, Philippe Leray, "Approches markovienne et semi-markovienne pour la modélisation de la fiabilité et des actions de maintenance d’un système ferroviaire", in Proceedings of 7e Conférence Francophone de MOdélisation et SIMulation MOSIM’08, Paris, France, 2008. |
| [11] | Martin Neil, Manesh Tailor, David Marquez, Norman Fenton, Peter Hearty, "Modelling Dependable Systems using Hybrid Bayesian Networks", Reliability Engineering and System Safety, Vol. 93, no. 7, pp. 933-939, 2008. |
| [12] | Benoît Lung, M. Veron, Marie Christine Suhner, Alexandre Muller, "Integration of Maintenance Strategies into Prognosis Process to Decision-Making Aid on System Operation", CIRP Annals - Manufacturing Technology, Vol. 54, no. 1, pp. 5-8, 2005. |
| [13] | Philippe Weber, Lionel Jouffe, "Complex System Reliability Modelling With Dynamic Object Oriented Bayesian Networks (DOOBN)", Reliability Engineering and System Safety, Vol. 91, no. 2, pp.149-162, 2006. |
| [14] | Orlando Borgia, Filippo De Carlo, Marco Peccianti, Mario Tucci, "The Use of Dynamic Object Oriented Bayesian Networks in Reliability Assessment: a Case Study", Recent Advances in Maintenance and Infrastructure Management, Springer-Verlag London Limited, London, England, 2009. |
| [15] | Olivier Francois, Laurent Bouillaut, Patrice Aknin, Philippe Leray, Stéphane Dubois, "Approche semi-markovienne pour la modélisation de stratégie de maintenance : application à la prévention de rupture du rail", in Proceedings of 7e Conférence Francophone de MOdélisation et SIMulation MOSIM’08, Paris, France, 2008. |
| [16] | Helge Langseth, Thomas D Nielsen, Rafael Rumí, Antonio Salmerón, "Inference in hybrid Bayesian networks", Reliability Engineering and System Safety, Vol. 94, no. 10, pp. 1499-1509, 2009. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML