-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Intelligent Systems
2012; 2(2): 12-17
doi: 10.5923/j.ajis.20120202.02
Improvement in Forecasting Accuracy Using the Hybrid Model of ARFIMA and Feed Forward Neural Network
Cagdas Hakan Aladag 1, Erol Egrioglu 2, Cem Kadilar 1
1Department of Statistics, Hacettepe University, Ankara, Turkey
2Department of Statistics, Ondokuz Mayis University, Samsun, Turkey
Correspondence to: Erol Egrioglu , Department of Statistics, Ondokuz Mayis University, Samsun, Turkey.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In recent years, autoregressive fractionally integrated moving average (ARFIMA) models have been used for forecasting of long memory time series in the literature. Major limitation of ARFIMA models is the pre-assumed linear form of the model. Since many time series in real-world have non-linear structure, ARFIMA models are not always satisfactory. Both theoretical and empirical findings in literature show that combining linear and non-linear models such as ARIMA and artificial neural networks (ANN) can be an effective and efficient way to improve forecasts. However, to model long memory time series, any hybrid approach has not been proposed in the literature. In this study, a new hybrid approach combining ARFIMA and feedforward neural networks (FNN) is proposed to analyze long memory time series. The proposed hybrid method is applied to tourism data of whose structure shows dominantly the characteristic of long term. Then, this hybrid method is compared with other methods and it is found that the proposed hybrid approach has the best forecasting accuracy.
Keywords: Feed forward neural networks, ARFIMA, Hybrid approach, Long memory
Article Outline
1. Introduction
- A popular class of models for time series with long memory behaviour is the ARFIMA(p,d,q) model ([27]). This kind of models extended classical ARIMA(p,d,q) models by assuming the differencing parameter d as a real value. It is well known that ARFIMA models are linear time series model. Since some long memory time series have both linear and non-linear structures, ARFIMA models can be inadequate for this type of series. Therefore, these time series are modeled by a hybrid of linear and non-linear models, and by this way forecast accuracy is improved.ANN have been widely used to model time series in various fields of applications[4] and used as a good alternative method for both linear and non-linear time series forecasting. Since ANN can model both non-linear and linear structures of time series, it is obvious that it can give good results in forecasting. As[37] mentioned, one of the most popular neural net paradigms is the feed forward neural network that is used in our study.[40]review the literature for forecasting time series by ANN.Both theoretical and empirical findings in literature show that combining different methods can be an effective and efficient way to improve forecasts. Therefore, hybrid of ARIMA and ANN methods has been used for modelling both linear and non-linear patterns equally well.[30] proposed hybrid ARIMA and support vector machines model.[38] combined seasonal time series ARIMA model and FNN.[41] introduced a hybrid of ARIMA and FNN models.Forecasting tourism data is an important task since it is employed for future planning. In the literature, there have been many studies using time series analysis in tourism data.[10],[39],[23-25], and[22] presented survey studies. Recently,[35] have summarized the studies on this topic in the last decade such as[18, 19, 5, 6, 17, 29] and[31]. Empirical results in all of these papers show that artificial neural networks can produce better results than those generated by conventional time series methods. However, ARFIMA models, which are also applied in our study while modelling the tourism data, have been found very successful for the analysis of tourism data in[7].In this paper, to model long memory time series which have both linear and non-linear structures, a new hybrid method is proposed by modifying[41] hybrid method. This paper aims to obtain better forecasting accuracy by modelling both linear and non-linear patterns of long memory time series. Therefore, if more accurate forecasts are obtained, better plans for activities of tourism will be made. The some hybrid methods have been proposed in[15], [16],[20],[28],[32],[33] and[41] studies. Although there have been some methods combine ARIMA and ANN models, the combination of ARFIMA and ANN models haven't proposed in the literature. The proposed method is the first study about combining of ARFIMA and feed forward neural network. The proposed method is applied to the tourism data of Turkey. This monthly data concerns the number of tourists coming to Turkey between the periods 1995:1-2005:12.The rest of the paper is organized as follows. In Sections 2 and 3, ARFIMA models and elements of FNN are presented, respectively. In Section 4, the proposed hybrid approach is introduced. In Section 5, the proposed method is applied to the tourism data of Turkey and compared with ARIMA, ARFIMA and FNN models. In the last section, the efficiency of the proposed method is discussed.
2. ARFIMA Models
- ARFIMA models are used to model long range dependent time series. ARFIMA models were introduced by[11]. ARFIMA(p,d,q) model can be given by
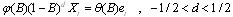 where B is the back-shift operator such that BXt=Xt-1 and et is a white noise process with E(ct)=o and variance
where B is the back-shift operator such that BXt=Xt-1 and et is a white noise process with E(ct)=o and variance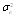 . The polynomials
. The polynomials 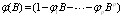 and
and 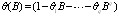 have orders p and q respectively with all their roots outside the unit circle.[3] extended the estimation of ARFIMA models for any
have orders p and q respectively with all their roots outside the unit circle.[3] extended the estimation of ARFIMA models for any 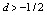 by considering the following variation of the ARFIMA model:
by considering the following variation of the ARFIMA model: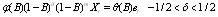 | (1) |
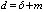 . General properties of ARFIMA models were given by Hosking[13, 14] and[2]. Studies about the parameter estimation of ARFIMA models still continue. Many maximum likelihood (ML) methods for ARFIMA are proposed in literature such as approximate ML methods (AML) by[12, 14, 21] and[2]; exact ML method (EML) by[36]; conditional sum of square (CSS) method by[8]. Note that CSS method is as efficient as EML method and it is identical with AML method by[2] that is based on infinity autoregressive presentation.
. General properties of ARFIMA models were given by Hosking[13, 14] and[2]. Studies about the parameter estimation of ARFIMA models still continue. Many maximum likelihood (ML) methods for ARFIMA are proposed in literature such as approximate ML methods (AML) by[12, 14, 21] and[2]; exact ML method (EML) by[36]; conditional sum of square (CSS) method by[8]. Note that CSS method is as efficient as EML method and it is identical with AML method by[2] that is based on infinity autoregressive presentation.3. Elements of FNN
- Elements of the ANN are network architecture, learning algorithm and activation function. Determining these elements that affect the forecasting performance of FNN should be considered carefully.One critical decision is to determine the appropriate architecture, that is, the number of layers, number of nodes in each layers and the number of arcs which interconnect with the nodes[42]. FNN has been used by many studies in forecasting. However, determining of the architecture is a basic problem. Since, in the literature, there is no general rule for determining the best architecture, many architectures can be considered as the correct architecture. Fig. 1 depicts the broad FNN architecture that has single hidden layer and single output.Learning of FNN for a specific task is equivalent to finding the values all of the weights such that the desired output is generated to the corresponding input. Various training algorithms have been used for the determination of the optimal weights values. The most popularly used training method is the back propagation algorithm ([34]). In the back propagation algorithm, learning of the ANN consists of adjusting all weights such as the error measure between the desired output and actual output ([9]).Another element of FNN is the activation function. It determines the relationship between inputs and outputs of a network. In general, the activation function introduces a degree of the non-linearity that is valuable most of the FNN applications. The well known activation functions are logistic, hyperbolic tangent, sine (or cosine) and the linear functions. Among them, logistic transfer function is the most popular one ([40]).
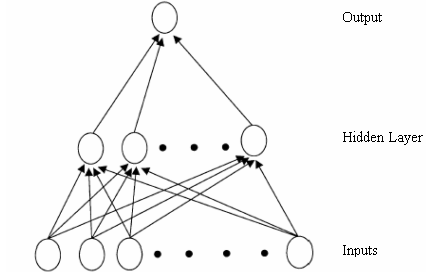 | Figure 1. A broad FNN architecture |
4. The Proposed Hybrid ARFIMA and FNN Approach
- ARFIMA processes have been used to model long memory time series. However, it is clearly that using ARFIMA processes for modelling non-linear problems is not adequate because ARFIMA model is based on a linear structure. Applications of hybrid methods in the literature show that combining different methods can be an effective and efficient way to improve forecasts. Since it is difficult to completely know the characteristics of data in a real problem, hybrid methodology which has both linear and non-linear modelling capabilities can be a good approach for practical purposes. Therefore, to model time series having both linear and non-linear structures, hybrid approaches are proposed. To model long memory time series, any hybrid approach has not been proposed in the literature. In this paper, by modifying Zhang’s[41] hybrid approach, a new hybrid approach is proposed to solve this problem. The proposed hybrid ARFIMA and FNN approach is given as follows:It is assumed that a time series can be considered composing of two components, which are a linear autocorrelation structure part and a non-linear part respectively. The model is as follows:
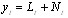 | (2) |
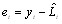 | (3) |
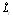 is the forecasting value for the period t of the time series yt by ARFIMA. Residuals are vital in examining the linearity assumption of the model. Autocorrelation coefficients are used to decide whether the residuals have linear relation or not. On the other hand, non-linear relation cannot be determined since the autocorrelation coefficient can be only employed for linear relation. Thus, the residuals might denote non-linear relation even though the autocorrelation coefficients for the residuals are approximately about zero. Therefore, the residuals obtained from the time series model generated by ARFIMA are analyzed by using FNN. With n input nodes, the FNN model for the residuals can be written as
is the forecasting value for the period t of the time series yt by ARFIMA. Residuals are vital in examining the linearity assumption of the model. Autocorrelation coefficients are used to decide whether the residuals have linear relation or not. On the other hand, non-linear relation cannot be determined since the autocorrelation coefficient can be only employed for linear relation. Thus, the residuals might denote non-linear relation even though the autocorrelation coefficients for the residuals are approximately about zero. Therefore, the residuals obtained from the time series model generated by ARFIMA are analyzed by using FNN. With n input nodes, the FNN model for the residuals can be written as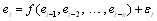 | (4) |
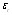 is the random error. The estimation of et by (4) will yield the forecasting of non-linear component of time series, Nt. By this way, forecasting values of the time series are obtained as follows:
is the random error. The estimation of et by (4) will yield the forecasting of non-linear component of time series, Nt. By this way, forecasting values of the time series are obtained as follows: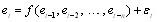 | (5) |
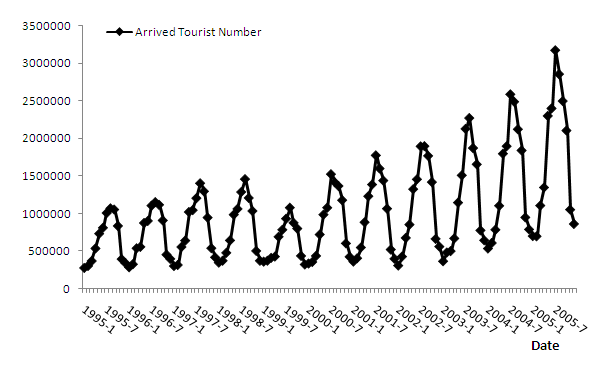 | Figure 2. The tourism data of Turkey |
5. Empirical Results
- The proposed hybrid method is applied to the tourism data of Turkey which is plotted in Fig. 2. This monthly data concerns the number of tourists coming to Turkey between the periods 1995:1-2005:12. For comparison, the data is also modeled by ARIMA, ARFIMA, and FNN. The last 24 observations of the data are used for comparing the methods by obtaining the values of root mean square error (RMSE), mean absolute percentage error (MAPE), median absolute percentage error (MdAPE) and the rest of the observations are used for the parameter estimation of the models.Firstly, the tourism data of Turkey is analysed by ARFIMA models. Tourism series has seasonality. Therefore, the stationary series yt can be given by
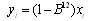 | (6) |
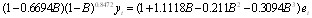 where et is found as a white noise series using Box-Pierce Test. RMSE value of forecasts obtained by using ARFIMA (1,d,3) model for last 24 data points is given in Table 1.Secondly, the tourism time series is directly analysed by two different FNN models. When the best architecture design was determining, trial and error method was used. Although some systematically approaches to determine architecture design exist in the literature, they are not preferred generally since they do not guarantee the best architecture. Thus, in the literature, the most preferred and used method to determine ANN structures in time series forecasting studies is trial and error method. And this method is performed relevant to considered data. ANN is also a method based on the data examined.Therefore, trial and error method is used in our study. The first used FNN model, which includes logistic activation function in the hidden layer and linear activation function in the output layer, is called FNN1. The other one, which includes logistic activation function in all layers, is called FNN2. For each FNN model, 144 architectures are examined by varying the number of neurons in the hidden layer and in the input layer 1 to 12. By these trials, the best architecture, which has the lowest RMSE value for the test set, is determined. For FNN1 model, the best architecture was found as FNN1(11-2-1), which includes 11 neurons in the input layer and 2 neurons in the hidden layer. FNN1(11-2-1) forecasts and the original tourism series of Turkey for 2004 and 2005 are shown in Table 1. In addition to this, calculated RMSE, MAPE, and MdAPE values for FNN1(11-2-1) are presented in Table 2.Similarly, the best architecture for FNN2 was found as FNN2(9-2-1). The forecast values for 2004 and 2005 are presented in the Table 1 and calculated RMSE, MAPE, and MdAPE values for FNN2(9-2-1) are given in the Table 3. Neural networks tool box of Matlab 7.0 version is used in the analysis.Finally, the tourism data is examined by employing the proposed hybrid approach presented in Section the first phase of the proposed method, the tourism data is analysed by ARFIMA model. As mentioned, ARFIMA (1,d,3) is determined as the most proper model. In the second phase, the residuals obtained in the first phase are analysed by using FNN1 and FNN2 models, separately. For each model, 144 architectures are examined by varying the number of neurons in the hidden layer and in the input layer 1 to 12. For FNN1 and FNN2 models, FNN1(9-1-1) and FNN2(1-1-1) are determined as the best architectures, respectively. Then, the predicted values obtained by ARFIMA(1,d,3) and FNN1(9-1-1) are summed. These results belong to the first hybrid method that is called Hybrid1. Similarly, the predicted values obtained by ARFIMA(1,d,3) and FNN2(1-1-1) are summed and the results of Hybrid2 are obtained. For 2004 and 2005, the forecast values obtained from the hybrid methods are presented in the Table 1. The values of RMSE, MAPE, and MdAPE for these two hybrid methods are given in Table 2. It is clearly seen from the results that when the FNN2 model is used in the hybrid model, better results are obtained. Therefore, we prefer to employ FNN2 model in the proposed hybrid method. From Fig. 3, we can observe the forecast values of all models.In Table 3, the values of RMSE, MAPE, and MdAPE for all methods are given for comparison. It is observed from this table that the proposed hybrid method gives the best results in terms of all used forecasting criteria since this method has the smallest values for all used criteria. Another important result is the two FNN models give the worst forecasts. Although FNN have proved success in forecasting time series, we see that the FNN models are ineffective for the data long memory structured.
where et is found as a white noise series using Box-Pierce Test. RMSE value of forecasts obtained by using ARFIMA (1,d,3) model for last 24 data points is given in Table 1.Secondly, the tourism time series is directly analysed by two different FNN models. When the best architecture design was determining, trial and error method was used. Although some systematically approaches to determine architecture design exist in the literature, they are not preferred generally since they do not guarantee the best architecture. Thus, in the literature, the most preferred and used method to determine ANN structures in time series forecasting studies is trial and error method. And this method is performed relevant to considered data. ANN is also a method based on the data examined.Therefore, trial and error method is used in our study. The first used FNN model, which includes logistic activation function in the hidden layer and linear activation function in the output layer, is called FNN1. The other one, which includes logistic activation function in all layers, is called FNN2. For each FNN model, 144 architectures are examined by varying the number of neurons in the hidden layer and in the input layer 1 to 12. By these trials, the best architecture, which has the lowest RMSE value for the test set, is determined. For FNN1 model, the best architecture was found as FNN1(11-2-1), which includes 11 neurons in the input layer and 2 neurons in the hidden layer. FNN1(11-2-1) forecasts and the original tourism series of Turkey for 2004 and 2005 are shown in Table 1. In addition to this, calculated RMSE, MAPE, and MdAPE values for FNN1(11-2-1) are presented in Table 2.Similarly, the best architecture for FNN2 was found as FNN2(9-2-1). The forecast values for 2004 and 2005 are presented in the Table 1 and calculated RMSE, MAPE, and MdAPE values for FNN2(9-2-1) are given in the Table 3. Neural networks tool box of Matlab 7.0 version is used in the analysis.Finally, the tourism data is examined by employing the proposed hybrid approach presented in Section the first phase of the proposed method, the tourism data is analysed by ARFIMA model. As mentioned, ARFIMA (1,d,3) is determined as the most proper model. In the second phase, the residuals obtained in the first phase are analysed by using FNN1 and FNN2 models, separately. For each model, 144 architectures are examined by varying the number of neurons in the hidden layer and in the input layer 1 to 12. For FNN1 and FNN2 models, FNN1(9-1-1) and FNN2(1-1-1) are determined as the best architectures, respectively. Then, the predicted values obtained by ARFIMA(1,d,3) and FNN1(9-1-1) are summed. These results belong to the first hybrid method that is called Hybrid1. Similarly, the predicted values obtained by ARFIMA(1,d,3) and FNN2(1-1-1) are summed and the results of Hybrid2 are obtained. For 2004 and 2005, the forecast values obtained from the hybrid methods are presented in the Table 1. The values of RMSE, MAPE, and MdAPE for these two hybrid methods are given in Table 2. It is clearly seen from the results that when the FNN2 model is used in the hybrid model, better results are obtained. Therefore, we prefer to employ FNN2 model in the proposed hybrid method. From Fig. 3, we can observe the forecast values of all models.In Table 3, the values of RMSE, MAPE, and MdAPE for all methods are given for comparison. It is observed from this table that the proposed hybrid method gives the best results in terms of all used forecasting criteria since this method has the smallest values for all used criteria. Another important result is the two FNN models give the worst forecasts. Although FNN have proved success in forecasting time series, we see that the FNN models are ineffective for the data long memory structured.
|
|
6. Conclusions
- Long memory time series have been analysed by using ARFIMA models which are based on linear structure. ARFIMA models are not always adequate for long memory time series that have both linear and non-linear structures. Therefore, the hybrid method which combines linear and non-linear models can be an effective way to improve forecasting performance. Motivated by this idea, in this paper, a hybrid model of ARFIMA and FNN is proposed to increase forecasting accuracy. Applying the proposed hybrid method to the tourism data of Turkey, we see that the proposed method is more successful than the other methods in terms of obtaining better forecasts. All computational processes related to neural networks are done with Matlab 7.0 software. As a result, the best forecasts are obtained by using the proposed hybrid ARFIMA and FNN2 (1-1-1) model. It is also seen that using only FNN models are ineffective for this long memory structured time series. This is also an important result for the ANN studies in the future. In further studies, we hope to improve the forecasting accuracy by changing the type of ANN in hybrid models presented here.
References
| [1] | Akaike, H., 1979, "A Bayesian extensions of the minimum AIC procedure," Biometrika 66, pp:237-242. |
| [2] | Beran, J., "Statistics for long-memory processes," Chapman&Hall/Crc. (1994). |
| [3] | Beran, J., "Maximum likelihood estimation of the differencing parameter for invertible short and long memory ARIMA models," Journal of Royal Statistical Society Series B 57 (4), (1995) pp:659-672. |
| [4] | Buhamra, S., Smaoui, N. and Gabr, M., "The Box-Jenkins analysis and neural networks: prediction and time series modeling," Applied Mathematical Modelling 27 (2003) pp:805-815. |
| [5] | Burger, C.J.S.C., Dohnal, M., Kathrada, M. and Law, R., "A practitioners guide to time series methods for tourism demand forecasting – a case study of Durban, " South Africa Tourism Management, 22 (2001) pp: 403-409. |
| [6] | Cho, V., A comparison of three different approaches to tourist arrival forecasting. Tourism Management 24 (2003) pp:323-330. |
| [7] | Chu, F.L., "A fractionally integrated autoregressive moving average approach to forecasting tourism demand.," Tourism Management 29 (2008) pp:79-88. |
| [8] | Chung, C.F. and Baillie, R.T. "Small sample bias in conditional sum of squares estimators of fractionally integrated ARMA models," Empirical Economics, 18, (1993) pp:791-806. |
| [9] | Cichocki, A. and Unbehauen, R., "Neural networks for optimization and signal processing," John Willey & Sons, New York, (1993). |
| [10] | Crouch, G.I., "The study of international tourism demand: A review of practice," Journal of Travel Research 33 (1994) pp: 41-54. |
| [11] | Granger, C.W.J. and Joyeux, R., "An introduction to long-memory time series models and fractionally differencing," Journal of Time Series Analysis 1(1) (1980) pp:15-29. |
| [12] | Haslett, J. and Raftery, A.E., "Space-time modeling with long-memory dependence: assessing Ireland’s wind power resources.," Applied Statistics 38 (1989) pp:1-50. |
| [13] | Hosking, J.R.M., "Fractionally differencing," Biometrika 68 (1) (1981) pp:165-176. |
| [14] | Hosking, J.R.M., Modeling persistence in hydrological time series using fractionally differencing. Water Resources Research 20 (12) (1984) pp:1898-1908. |
| [15] | Khashei M. and Bijari M., "A new hybrid methodology for nonlinear time series forecasting," Modelling and Simulation in Engineering (doi: 10.115/2011/379121) (2011). |
| [16] | Khashei M. and Bijari M., "Hybridization of the probabilistic neural networks with feed forward neural networks for forecasting," Engineering Applications in Artificial Intelligence (doi: 10.1016/j.engappai.2012.01.019) (2012). |
| [17] | Kon, S.C. and Turner, W.L., "Neural network forecasting of tourism demand. Tourism Economics," 11(2005) pp:301-328. |
| [18] | Law, R., "Back-propagation learning in improving the accuracy of neural network –based tourism demand forecasting," Tourism Management 21 (2000) pp:331-340. |
| [19] | Law, R, "The impact of the Asian financial crisis on Japanese demand for travel to Hong Kong: A study of various forecasting techniques.," Journal of Travel &Tourism Marketing 10 (2001) pp:47-66. |
| [20] | Lee Y.S., Tong L.I., "Forecasting time series using a methodology based on autoregressive integrated moving average and genetic programming," Knowledge-Based Systems 24(1) (2011) pp:66-72. |
| [21] | Li, W.K. and McLeod, A.I., Fractional time series modeling. Biometrika 73 (1986) pp:217-221. |
| [22] | Li, G., Song, H. and Witt, S.F., 2005. Recent developments in econometrics modeling and forecasting. Journal of Travel Research, 44, pp:82-99. |
| [23] | Lim, C., "Review of international tourism demand models," Annals of Tourism Research 24 (1997) pp:835-849. |
| [24] | Lim,C. "An econometric classification and review of international tourism demand models," Tourism Economics 3 (1997) pp:69-81. |
| [25] | Lim,C., "A meta analysis review of international tourism demand," Journal of Travel Research 37 (1999) pp:273-284. |
| [26] | Lo, A.W., "Long memory in stock market prices," Econometrica 59, (1991) pp:1279-1313. |
| [27] | Man, K.S., "Long memory time series and short term forecasts," International Journal of Forecasting 19 (3) (2003) pp:477-491. |
| [28] | Min Gan, Hui Peng, "Stability analysis of RBF network-based state dependent autoregressive model for nonlinear time series," Applied Soft Computing 12(1) (2012) pp:174-181. |
| [29] | Pai, P.F., Hong, W.C., Chang, P.T. and Chen C.T., "The application of support vector machines to forecast tourist arrivals in Barbados: An empirical study," International Journal of Management, 23 (2006) 375-385. |
| [30] | Pai, P.F. and Lin, C.S., "A hybrid ARIMA and support vector machines model in stock price forecasting," The International Journal of Management Science 33(2005) pp:497-505. |
| [31] | Palmer, A., Jose Montano, J.J. and Sese, A., "Designing an artificial neural network for forecasting tourism time-series," Tourism Management 27 (2006) pp:781-790. |
| [32] | Purwanto, Eswaran, C., Logeswaran, R., "An optimally configured hybrid model for healthcare time series prediction," Asian Journal of Information Technology 10 (6) (2011) pp. 209-217. |
| [33] | Samsudin, R., Saad, P., Shabri, A., "A hybrid GMDH and least squares support vector machines in time series forecasting ," Neural Network World 21 (3) (2011) pp. 251-268. |
| [34] | Smith, K.A., "Neural networks in business: Techniques and applications," Imprint Info Hershey: Idea Group, (2002). |
| [35] | Song, H. and Li, G., "Tourism demand modeling and forecasting- A review of recent research.," Tourism Management 29 (2008) pp:203-220. |
| [36] | Sowell, F., "Maximum likelihood estimation of stationary univariate fractionally integrated time series models," Journal of Econometrics 53 (1992) pp:165-188. |
| [37] | Tang, Z., Almeida, C. and Fishwick, P.A., "Time series forecasting using neural networks vs. Box-Jenkins methodology," Simulation 57 (1991) pp:303-310. |
| [38] | Tseng, F.M., Yu, H.C. and Tzeng, G.H. "Combining neural network model with seasonal time series ARIMA model," Technological Forecasting and Social Change 69 (2002) pp:71-87. |
| [39] | Witt, S.F. and Witt, C.A., "Forecasting tourism demand: A review of empirical research," International Journal of Forecasting, 11 (1995) pp:447-475. |
| [40] | Zhang, G., Patuwo, B.E. and Hu, Y.M., Forecasting with artificial neural networks: The state of the art. International Journal of Forecasting 14 (1998) 35-62. |
| [41] | Zhang, G., "Time series forecasting using a hybrid ARIMA and neural network model," Neurocomputing, 50, (2003) 159-175. |
| [42] | Zurada, J.M., "Introduction of artificial neural systems" St. Paul: West Publishing, (1992). |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML