-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Intelligent Systems
p-ISSN: 2165-8978 e-ISSN: 2165-8994
2011; 1(1): 1-9
doi:10.5923/j.ajis.20110101.01
Spin Glass Automata (SGA): An Evolutionary Local Search Automata for Solving Optimization Problems
M. V. Jahan1, S. M. S. Kenari2
1Software Engineering Department, Mashhad Branch, Islamic Azad University, Mashhad, Iran
2Software Engineering Department, Nowshahr Branch, Islamic Azad University, Mazandaran, Iran
Correspondence to: M. V. Jahan, Software Engineering Department, Mashhad Branch, Islamic Azad University, Mashhad, Iran.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Nowadays, new optimization problems become so complicated that popular classic methods are unable to solve them in a reasonable time. By using heuristic and evolutionary algorithms, these problems can be solved more quickly. Cellular Automata (CA) and Spin Glasses (SG) are examples of such algorithms. A CA is a self-organized machine with a simple structure and complicated behavior. Due to local interactions between its cells, it has a high speed; however, it is unable to solve optimization problems. On the other hand, SGs, due to inter-spin magnetic interaction as well as following thermodynamic rules, continually have the tendency toward lower energy, and this way it can solve optimization problems. The interactions between spins are usually limited and consequently, aforementioned methods cannot solve optimization problems with an expected accuracy and this is a great impact. In this paper, with inspiration from behavior of CA and SG, a new machine named Spin Glass Automata (SGA) is introduced which has behavioral dynamic of SG and CA. It has also the ability of parallel processing while it is rapid enough. It follows rules of a CA too. With these properties at hand, the machine can be used in a vast area of optimization problems. Behavioral dynamic tests of the machine include phase transition, entropy and correlation as well as the comparison to other heuristic algorithms such as (GA, TS, SA and NN) shows the ability of this machine in solving practical optimization problems. It has an appropriate execution speed and accuracy. To test full potential of this machine, the NP problem such as optimal portfolio selection has been solved and compared with the five famous stock market of the world.
Keywords: Spin Glass Model, Portfolio Selection, Cellular Automata, Phase Transition and Parallel Processing
Cite this paper: M. V. Jahan, S. M. S. Kenari, Spin Glass Automata (SGA): An Evolutionary Local Search Automata for Solving Optimization Problems, American Journal of Intelligent Systems, Vol. 1 No. 1, 2011, pp. 1-9. doi: 10.5923/j.ajis.20110101.01.
Article Outline
1. Introduction
- Heuristic algorithms are the strongest classes of optimization algorithms which are receiving more attention and application increasingly. Due to a great extension in practical problem domains and increasing of the need for rapid information processing, parallel processing and rapid problem solver algorithms becomes more important. Most of parallel processing enable algorithms are inspired with natural processing. The main idea of these algorithms is local processing and global conclusion which namely are parallel genetic algorithms, parallel colony ants, parallel simulated annealing[1], cellular automata[2] and spin glasses[3].CA is a self-organized machine that is composed of an array of cells which each of them can own several finite states and can be updated through specific rules, discretely and simultaneously. While having the ability of parallel and local processing, this machine has a great speed in processing, too[2]. Behavioral dynamic of these machines, generally ends to specific finite states and this ability is denoted as self-organizing[4]. Aforementioned properties caused these machines to be used in encryption[5], image processing[5] and physical behavior simulating[6,7]. The great inabilities of the automata are, being unknown rules and inability in solving engineering problems specially optimization problems[6].SG is a network of spins in which spins interact magnetically and consistently change their values to achieve a lower level of energy. When the system is in minimum energy (or temperature) state, there is no significant variation in spin values and the system has reached ground state (the state with minimum energy)[8]. This model has many characteristics among which are non-exponential growth of ground states with an increase in the number of spin bonds, effectiveness of environmental factors such as temperature on network behavior and ability to achieve the optimum state at variant temperatures[9]. Also, in this model, each spin is a portion of solution while for example in genetic algorithms a chromosome is, of problem solutions itself[10]. Since the model is physically well specified, via modeling behavior of some engineering problems through it, one can solve these problems which are otherwise unsolvable conveniently [11,12].The differences between SG and CA are that SGs follows thermodynamic rules, they are based on temperature (it is temperature that define the final state of SGs), Spins have interactions in the network and the system has a energy function (or Hamiltonian function)[8]; while CA is based on time (it is time that define the final state of automata), cells have no interaction between themselves, only interact according to defined rule and have no defined energy function [2].In this paper, a new machine named spin glass automata (SGA) is introduced, which not only has the properties of CA but also follows thermodynamic rules of SG. In other words, this automata has the property of self-organizing, in specific temperature, has local behavior and cells are interacted with each other through defined rules. Furthermore, this machine has the ability of parallel and simultaneous processing capability that can solve optimization problems more efficiently.To study dynamic of this machine, testing upon random data can be an option but due to lack of a performance metric, it will be uncertain. Therefore the problem of optimal portfolio selection with initial constraints that is a non-deterministic polynomial problem (NP-Complete) is solved by this machine as a case study. Results of this experiment with actual data are compared and evaluated against accurate results from five well-known stock market of the world. The machine shows desirable speed and accuracy in solving the problem. In addition to aforementioned experiments, the dynamic of SGA is investigated through phase transition, correlation and entropy analysis. Finally, the performance of the automata is evaluated, in solving optimal portfolio selection problem, against that of four famous heuristic algorithms namely as genetic algorithm(GA), simulated annealing(SA), tabu search(TS) and neural network(NN).Therefore, first in section 2, the related activities to spin glasses are described as well as the combination of cellular automata and spin glasses. In sections 3 and 4, a nominal presentation of cellular automata and spin glasses are presented. In section 5, SGA and the problem of optimal portfolio selection are introduced. In section 6, experimental results such as the phase transition, entropy analysis and correlation test, are introduced to evaluate trustiness of prescribed method based on the fundamental data from five stock market of the world. Furthermore, execution speed and accuracy as well as Pareto front of the machine is compared to that of four well-known heuristic algorithms (SA, GA, TS and NN).
2. Related Activities
- CA is a simple and rapid machine and its operation is done locally with the ability of parallel processing. This way, the hardware implementation of the machine against other similar models, becomes simpler[2]. CA was used in encryption, compression and image processing[4]. It has also applications in chemical processes simulation, traffic and numerical calculus[13].SG is used in solving a lot of optimization problems. As an example, Hartmann et al. in[11,12] introduced several engineering problems such as Maximum Flow and Matching. Nishimori in[14,15], has investigated application of SGs for data transfer in noisy environment. In[16], Horiguchi et al. introduced routing in adaptive and distributed computer networks as another application area. Gabor et al. in[17] are the first ones who used spin glass to solve optimal portfolio selection problem. Finally, Akbarzadeh and Vafaei Jahan are pioneers who introduced a rapid method in[3] which could find optimal state with an appropriate accuracy for spin glasses with a limited bonds (limited connection) and that are using migration and elite operators (similar to genetic algorithm operators).SG and CA, has been combined in several ways in the past. As an example in[18], the Ising model is simulated using CA in a way that introduced cellular automata demonstrates Ising model like behaviors. In[19], an Ising cellular automata (ICA) is introduced which has thermodynamic properties of Ising model. Also in[20], the Q2R rules are introduced which caused, cellular automata to be used as an Ising model simulator but in the absence of thermal effects.
3. Cellular Automata
- CA is a simple machine which is able to show complex behavior. Mathematical model of the machine is a four tuple {A, S, N, f}, where Z is the cellular network of automata. S is the set of possible values each cell can own. N is the adjacent set of each cell and finally
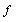 is transition rule or rule briefly. At each time, the value of cell S can be reached through applying rule f on the adjacent set N[2]. If all cells of the CA include a same rule, it is called homogenous CA and is called heterogeneous otherwise[2,6]. If boundary cells (first and last cells) are neighbors, the cellular automata is called CA with circular boundary and non-circular otherwise [2,6].
is transition rule or rule briefly. At each time, the value of cell S can be reached through applying rule f on the adjacent set N[2]. If all cells of the CA include a same rule, it is called homogenous CA and is called heterogeneous otherwise[2,6]. If boundary cells (first and last cells) are neighbors, the cellular automata is called CA with circular boundary and non-circular otherwise [2,6].4. Spin Glass
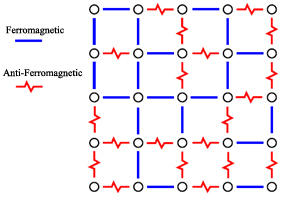
- Ising model is a network of spins which has either value of +1 or -1. These spins are interacted with each other according to a magnetic property among themselves and continually change themselves to reach lower energy level. Once the network is in the lowest energy level, no additional change will be seen in spin values and the network reaches ground state. Spin Glass Ising model is the same as Ising model except the value of each spin is between[-1,+1] rather than -1 and +1. This model is briefly called Spin Glass, too[8].Theoretically, SG, is a network of N spins that its structure can be either limited connection (connection with adjacent spins e.g. with 2D or 3D structure) or full connection1 (connection between each spin to all other spins). Spins have either ferromagnetic or anti-ferromagnetic property. According to before mentioned properties, network energy is calculated using the following formula[8,12]:
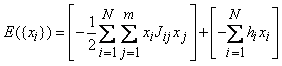 | (1) |
 is the energy of all spins, The sum
is the energy of all spins, The sum  ,
, runs over all pairs of nearest neighbors,
runs over all pairs of nearest neighbors, 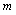 is the number of nearest neighbors of each spin
is the number of nearest neighbors of each spin 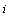 that can be
that can be 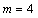 in Van Neumann cellular automata (CA) or
in Van Neumann cellular automata (CA) or 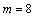 in Moore CA [16] or
in Moore CA [16] or 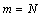 for full connection.
for full connection. 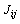 denotes the strength of the bond connecting spins
denotes the strength of the bond connecting spins 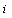 and
and 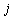 .
. 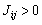 describes a ferromagnetic interaction, while
describes a ferromagnetic interaction, while 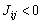 describes an anti-ferromagnetic interaction. The quantity
describes an anti-ferromagnetic interaction. The quantity 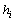 is the external field acting on spin
is the external field acting on spin 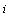 and describes the energy due to the spin's orientation. Also, the factor
and describes the energy due to the spin's orientation. Also, the factor 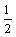 corrects for double counting of the interaction between every two neighboring spins. Here the task is to find a spin configuration
corrects for double counting of the interaction between every two neighboring spins. Here the task is to find a spin configuration 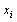 that minimizes the energy of the spin glass, given {
that minimizes the energy of the spin glass, given {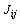 }, {
}, {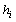 }. A scheme for a 2D spin glass is depicted in Figure 1.
}. A scheme for a 2D spin glass is depicted in Figure 1.5. Spin Glass Automata
- In this paper, a 2D spin glass CA is defined as an ordered 6-tuple
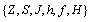 such that Z is a 2D network where each spin (cell) can interact with adjacent ones based on Van Neumann or Moore models (short range spin glass);
such that Z is a 2D network where each spin (cell) can interact with adjacent ones based on Van Neumann or Moore models (short range spin glass); 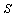 is the value of each spin can take between[0,1]; Each spin has an interaction (bond) with its nearest neighbor; A strength of the bond
is the value of each spin can take between[0,1]; Each spin has an interaction (bond) with its nearest neighbor; A strength of the bond 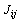 exists between each pair neighbor spins; The quantity
exists between each pair neighbor spins; The quantity 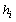 is the external field acting on spin
is the external field acting on spin 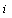 and describes the energy due to the spin’s orientation; The rule is the interaction rule between nearest neighbors which can be any defined rules for the Automata (It is the same as CA rules). This rule defines the type of interactivity; and
and describes the energy due to the spin’s orientation; The rule is the interaction rule between nearest neighbors which can be any defined rules for the Automata (It is the same as CA rules). This rule defines the type of interactivity; and 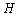 is Hamiltonian function of interaction or energy function for the whole automata. It usually constitutes of interactions between composer parts of the system and is calculated based on the problem type[8], and finally, it is calculated similar to Hamiltonian rule of SG.In SGA, the subsequent state of a spin is related to current states of the spin and its nearest neighbors and is specified based on rule
is Hamiltonian function of interaction or energy function for the whole automata. It usually constitutes of interactions between composer parts of the system and is calculated based on the problem type[8], and finally, it is calculated similar to Hamiltonian rule of SG.In SGA, the subsequent state of a spin is related to current states of the spin and its nearest neighbors and is specified based on rule 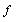 . Since SGA is moving through losing energy
. Since SGA is moving through losing energy 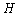 , the amount of spins' interaction energy
, the amount of spins' interaction energy 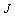 and external field energy
and external field energy 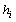 , together prevent spins to take any value
, together prevent spins to take any value 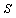 , i.e. only change which can cause any decrease in SGA's energy will be accepted.When the SGA starts, by using rule f and interactions with its neighbors, each spin tries to decrease its energy (changes its value) according to function H. if the change in value results in local energy decrease, the change will be accepted and with probability of
, i.e. only change which can cause any decrease in SGA's energy will be accepted.When the SGA starts, by using rule f and interactions with its neighbors, each spin tries to decrease its energy (changes its value) according to function H. if the change in value results in local energy decrease, the change will be accepted and with probability of 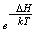 otherwise; where k is Boltzmann's constant and T is the environment temperature. Experiments show that in spite of local energy reduction, global decrease is also observed in the machine. Therefore the machine is useful in optimization problem solving.Using SG properties, the aforementioned SGA can follow thermodynamic rules and goes through equilibrium in any temperatures. Also through using CA capabilities, it can use any rule of it and produce finite states. The advantage of SGA against two other prior models is that it can show stable state based on any interaction rules between spins. If SGA temperature be high, it can produce all possible states. If temperature reduces, the automata goes through equilibrium with environment via losing energy.
otherwise; where k is Boltzmann's constant and T is the environment temperature. Experiments show that in spite of local energy reduction, global decrease is also observed in the machine. Therefore the machine is useful in optimization problem solving.Using SG properties, the aforementioned SGA can follow thermodynamic rules and goes through equilibrium in any temperatures. Also through using CA capabilities, it can use any rule of it and produce finite states. The advantage of SGA against two other prior models is that it can show stable state based on any interaction rules between spins. If SGA temperature be high, it can produce all possible states. If temperature reduces, the automata goes through equilibrium with environment via losing energy.5.1. SGA Dynamics
- Structural and behavioral dynamic studies of the machine, requires investigations such as thermodynamic behavior of it in various temperatures, entropy changes, the amount of energy decrease to minimum at equilibrium temperature and also phase transition temperature which are all dealt with in detail in the next section. To evaluate dynamic of the proposed machine, a case study is inevitable. To this end, the non-polynomial problem of optimal portfolio selection is chosen. The selection shows not only ability of the machine to solve engineering problems, but also its behavioral dynamic based on real data.In this paper, a heterogeneous 2D SGA with non-circular boundary condition is used which spin values S include all real numbers in[0,1] and the state of each spin changes because of interactions with adjacent spins. The rule
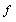 is an average rule which is calculated via summation of the nearest neighbors values divided by their total count. The Hamilton function
is an average rule which is calculated via summation of the nearest neighbors values divided by their total count. The Hamilton function 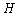 , is the energy function of formula (1) which its calculation method is described in the next section.
, is the energy function of formula (1) which its calculation method is described in the next section.5.2. Portfolio Selection Problem and SGA
- Portfolio selection problem [20] is stated by Markowitz model as if
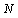 stocks are assumed and for each stock
stocks are assumed and for each stock 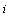 ,
, 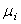 is the mean return of asset
is the mean return of asset 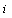 , and
, and 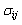 is the covariance between returns of assets
is the covariance between returns of assets 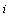 and
and 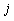 . The decision variable
. The decision variable 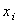 represents the fraction of capital to be invested in asset
represents the fraction of capital to be invested in asset 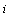 . following multi-objective problem has to be optimized:
. following multi-objective problem has to be optimized: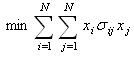 | (2) |
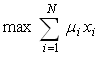 | (3) |
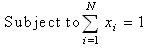 | (4) |
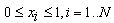 | (5) |
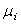 is achieved from mean return of each asset in defined intervals, in such a way that if
is achieved from mean return of each asset in defined intervals, in such a way that if 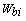 be value of stock i in beginning of the interval and
be value of stock i in beginning of the interval and 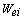 be that of interval end, then
be that of interval end, then 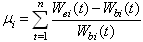 where n will be the number intervals which stock i is considered in.In this paper, for a simpler solving of the multi-purpose problem, it converts to a multi-modal problem:
where n will be the number intervals which stock i is considered in.In this paper, for a simpler solving of the multi-purpose problem, it converts to a multi-modal problem: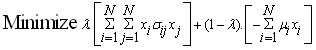 | (6) |
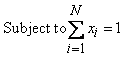 | (7) |
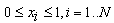 | (8) |
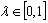 is called risk aversion parameter. It shows the amount of risk effects in optimization function. If
is called risk aversion parameter. It shows the amount of risk effects in optimization function. If 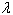 =0 then Eq. (5) represents maximum portfolio mean return (without considering the variance) and the optimal solution will be formed only by the asset with the greatest mean return. The case with
=0 then Eq. (5) represents maximum portfolio mean return (without considering the variance) and the optimal solution will be formed only by the asset with the greatest mean return. The case with 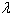 =1 represents minimizing the total variance associated with the portfolio (regardless of the mean returns) and the optimal solution will typically consist of several assets. Any value of
=1 represents minimizing the total variance associated with the portfolio (regardless of the mean returns) and the optimal solution will typically consist of several assets. Any value of 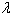 inside the interval (0,1) represents a tradeoff between mean return and variance, generating a solution between the two extremes,
inside the interval (0,1) represents a tradeoff between mean return and variance, generating a solution between the two extremes, 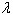 = 0 and 1.To solve optimal portfolio selection problem, as is also investigated in [3], it is assumed that each stock is a spin which has a value between 0 and 1. This automata owns an energy function like formula (1) while the problem goal is to select an optimal portfolio and to minimize formula (6). Thus, through the following mapping formula (6) can be converted to the formula (1):
= 0 and 1.To solve optimal portfolio selection problem, as is also investigated in [3], it is assumed that each stock is a spin which has a value between 0 and 1. This automata owns an energy function like formula (1) while the problem goal is to select an optimal portfolio and to minimize formula (6). Thus, through the following mapping formula (6) can be converted to the formula (1):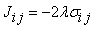 | (9) |
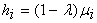 | (10) |
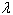 takes a number greater that 0 and lower than 1 (to be equal the effects of risk and mean return, value of 0.5 is selected). The approach, each spin interacts with its nearest neighbors, is such that the amount of each spin is summed with its nearest ones and is averaged while limitations of (4) and (5) are satisfied all over the process. Now, when the machine starts at a random state, through neighbor spins interactions and consequently spins value changes, it tries to find the lowest amount of energy at the current temperature. Since the lowest amount of energy is also the value of cost function (6), states of spins will show optimal portfolio at temperature near to zero.
takes a number greater that 0 and lower than 1 (to be equal the effects of risk and mean return, value of 0.5 is selected). The approach, each spin interacts with its nearest neighbors, is such that the amount of each spin is summed with its nearest ones and is averaged while limitations of (4) and (5) are satisfied all over the process. Now, when the machine starts at a random state, through neighbor spins interactions and consequently spins value changes, it tries to find the lowest amount of energy at the current temperature. Since the lowest amount of energy is also the value of cost function (6), states of spins will show optimal portfolio at temperature near to zero.6. Experimental Results
- To evaluate performance of proposed machine, Experiments on the benchmark data were originally performed in [21]. These benchmark data are presented in text file format as follows: Number of assets (N); and for each asset i (i=1,...,N): mean return as well as standard deviation of return; for all possible pairs of assets: i, j, correlation between asset i and asset j. The above data were taken from five major stock exchange markets, during the time period extending from March 1992 to September 1997. These five stock exchange markets include Hang Seng in Hong Kong (31 assets), Deutscher Aktien Index (DAX100) in Germany (85 assets), Financial Times London Stock Exchange (FTSE100) in Britain (89 assets), Standard & Poor's (S&P100) in USA (98 assets), and Nikkei in Japan (225 assets). Probability density function (pdf) of covariance P (J) of each stock market for the given data has been shown in Figure. 2.
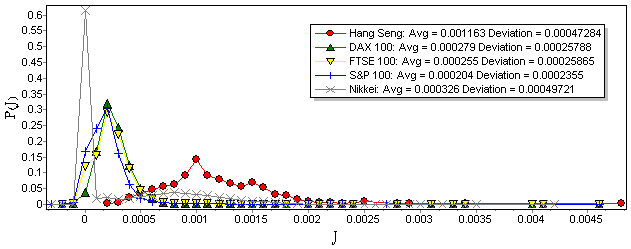 | Figure 2. Probability density functions for covariances between assets in 5 major stock markets from 1992 to 1997 from data in[21] |
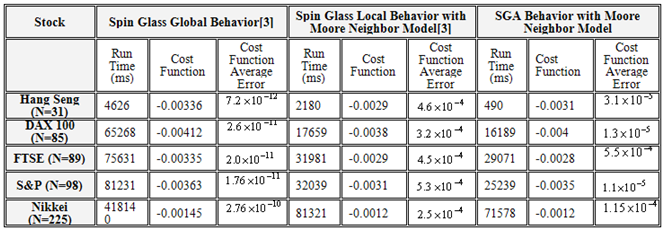
6.1. SGA Dynamic: Local Behavior with Parallel Processing Ability
- Experiments show that local behavior of SGA results in a considerable increase in convergence speed. In Table (2), run time of proposed algorithm is presented. As is shown the run time is so much better than global behavior of glass and ever its local behavior. But response accuracy is acceptable while is less than that of global behavior. This shows that trapping in local optimum is possible yet. Among the factors which speed up SGA, is its absolute local while targeted behavior which causes, as an instance for stock market Nikkei, response time to be 6 times more than that of global behavior while the accuracy is appropriate. This local behavior brings machine with parallel processing capability. Experiment results shown in table (1), which is to investigate parallel processing capability of this algorithm and for various stocks, show that parallel processing ability of the process can considerably speeds up it. To this end, in this experiment, it is possible to break down the automata into smaller and discrete automatas and to run each automata on one processor (breaking down method doesn't follow any predefined rule and can be done arbitrarily).
6.2. SGA Dynamic: Phase Transition
- Phase transition typically refers to a transformation of a thermodynamic system from one state to another. This transformation is typically marked by a sudden change in some physical property as a result of a small change in what is called an order parameter (e.g., temperature)[26,27]. Here, the critical temperature
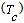 of SGA is the temperature at which phase transition occurs. At this temperature, the probability of reaching the ground state of the glass changes significantly, i.e. automata's states become more/less unlikely to be a ground state. Figure. 3, illustrates critical temperature of SGA applied to the portfolio selection problems. As shown in this figure, the probability of reaching ground state (
of SGA is the temperature at which phase transition occurs. At this temperature, the probability of reaching the ground state of the glass changes significantly, i.e. automata's states become more/less unlikely to be a ground state. Figure. 3, illustrates critical temperature of SGA applied to the portfolio selection problems. As shown in this figure, the probability of reaching ground state (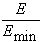 ) is equal to 1 in low temperatures, where
) is equal to 1 in low temperatures, where 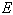 is the amount of SGA energy and
is the amount of SGA energy and 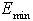 is the actual minimum of the energy function. As temperature rises, glass energy also changes and the probability of reaching ground state is expected to gradually decrease. However, this drop is delayed until phase transition where a sudden drop occurs (In this paper, phase transition is defined to occur at
is the actual minimum of the energy function. As temperature rises, glass energy also changes and the probability of reaching ground state is expected to gradually decrease. However, this drop is delayed until phase transition where a sudden drop occurs (In this paper, phase transition is defined to occur at 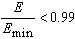 ). After the critical temperature, the probability of reaching ground state decreases significantly. Figure 3 illustrates the phase transition for the five stock markets in this paper. The vertical solid red line on
). After the critical temperature, the probability of reaching ground state decreases significantly. Figure 3 illustrates the phase transition for the five stock markets in this paper. The vertical solid red line on 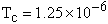 highlights the proximity of this transition for most of the benchmarks. After this temperature, system is not likely to be in its optimal ground state. The dashed gray lines indicate the range of critical temperature for different benchmarks.
highlights the proximity of this transition for most of the benchmarks. After this temperature, system is not likely to be in its optimal ground state. The dashed gray lines indicate the range of critical temperature for different benchmarks.
|
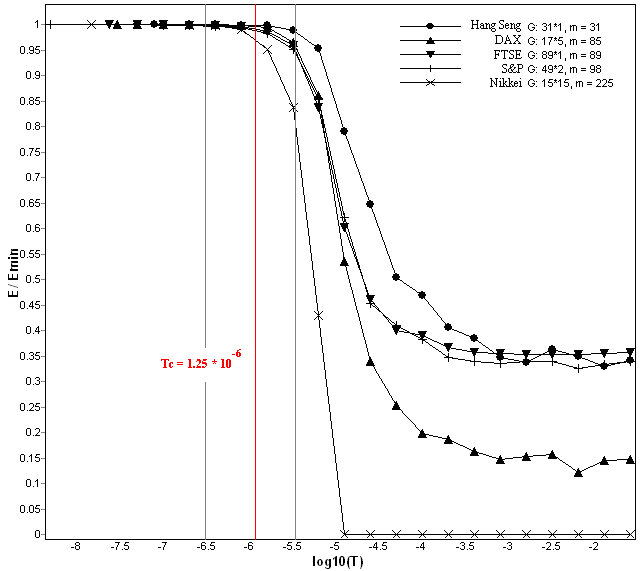 | Figure 3. SGA Phase Transition Temperature for the 5 stock markets mentioned in[21]. Phase Transition Temperatures are almost equal for all stocks |
6.3. SGA Dynamic: Correlation Test
- The correlation test is used to verify the correctness of our previous test as follows. Two randomly distributed SGAs are independently considered on same stock market data. Both Automatas are used to find the ground state separately. The rate of correlation is then calculated for the two glasses (in lieu of amount of each corresponding cell). The correlation level at each temperature is determined as follows:
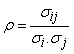 | (11) |
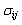 is the covariance of spins between two corresponding spins of each glass, and
is the covariance of spins between two corresponding spins of each glass, and 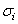 and
and 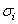 are the standard deviation of cells of SGA
are the standard deviation of cells of SGA 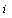 and
and 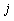 , respectively.
, respectively.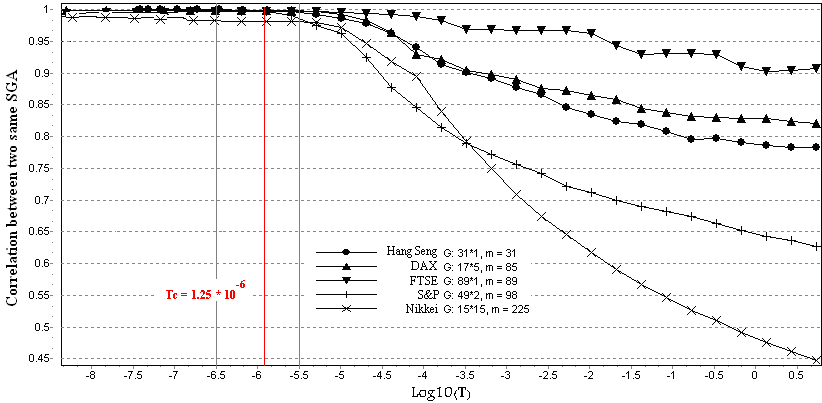 | Figure 4. Correlation test of the two SGAs for same stock market |
6.4. SGA Dynamic: Entropy Analysis
- According to third thermodynamic rule, in near zero temperature, system has its minimum entropy. In another experiment it is shown that the rule is valid for SGA while is invalid for CA[22,23]. In equilibrium temperature, the probability by which system is placed in state i depends on system energy on that state and is calculated through the following equation[24]:
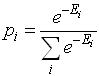 | (12) |
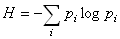 | (13) |
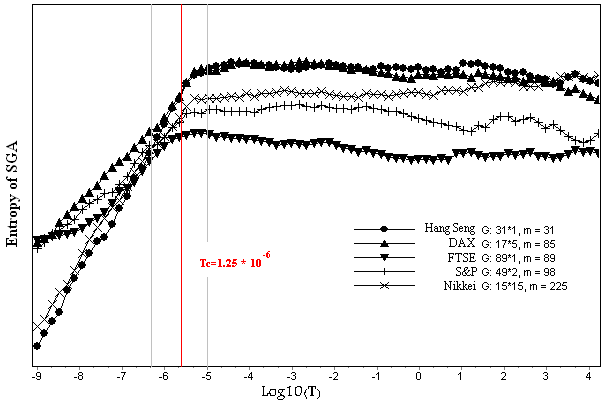 | Figure 5. SGA entropy for solving optimal portfolio selection problem |
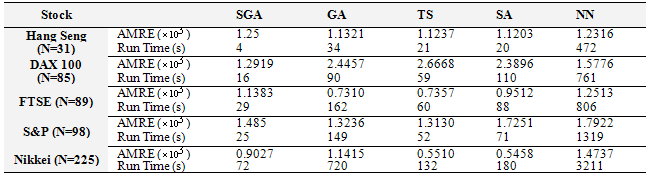
7. SGA and Other Heuristic Algorithms
- SGA performance is evaluated against other heuristic algorithms in another experiment. Table (3) represents SGA behavior against that of four optimization problem solver algorithms. As illustrated in the table, SGA convergence speed is more than that of optimization methods GA, TS, SA and NN which are investigated in[25] (The run time of the proposed method and the current methods in paper[25], due to the differences in computers and similar simulation software, is not the same. Because, the authors implement the GA, TS, SA and NN, according to the author's understanding of the paper[25]; in table (3) the new run time results have been listed. Some differences in the experimental run time results is observed but the conclusion seems generally correct), while its accuracy in finding result is already acceptable. As an instance for Nikkei and Hang Seng stock market, the convergence speed is more considerably.
|
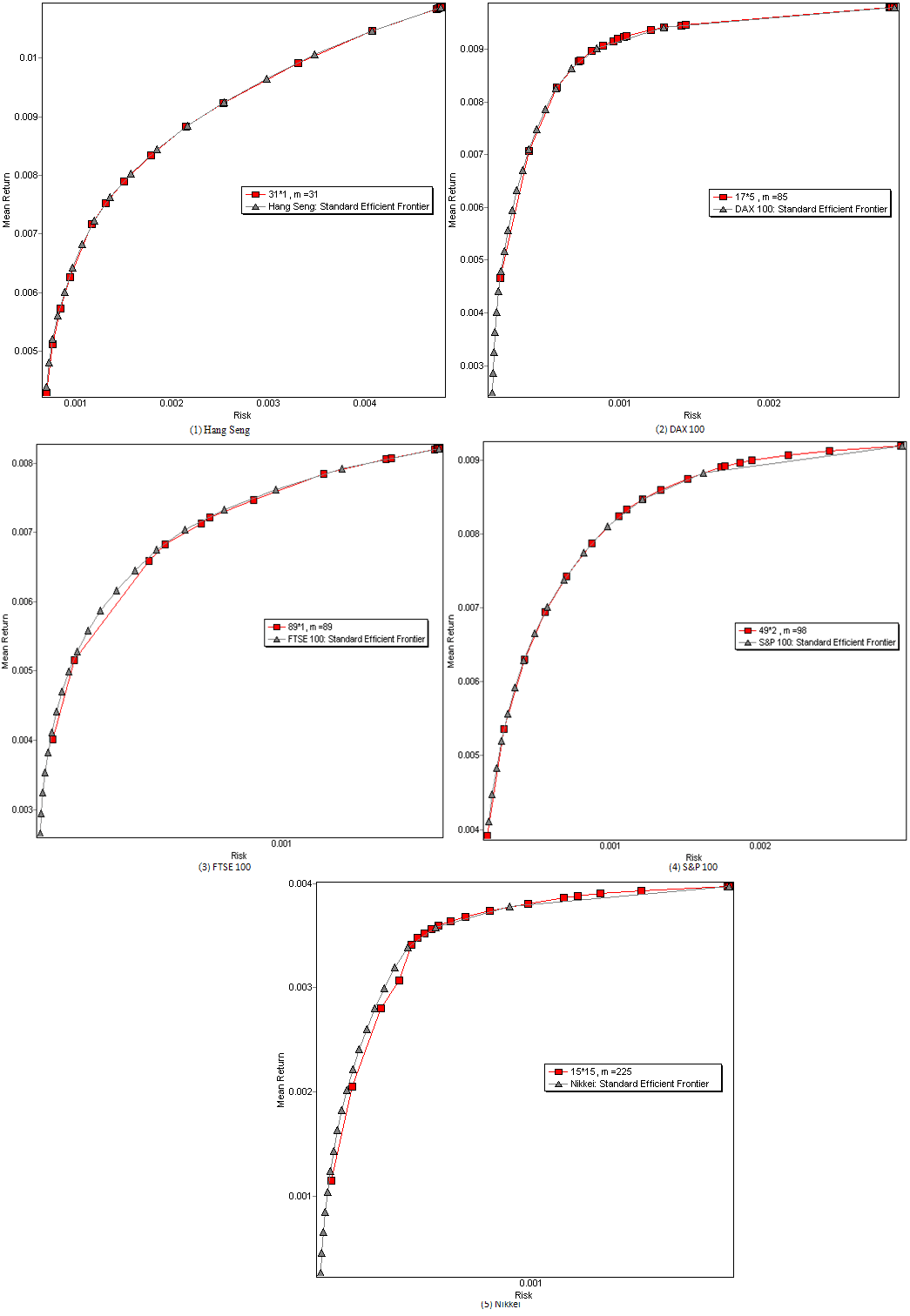 | Figure 6. The Pareto front resulted from running SGA against standard optimal front resulted from benchmark data of[21] |
8. SGA Pareto Front and Comparison to Optimal Front
- In another experiment optimal outcomes front resulted from SGA with various λs is depicted. In Figure. 6 movement path is toward to Pareto front and for the 5 aforementioned stock market, shows validity of energy decrease and finding result. In the figure, resulted optimal Pareto front for various λs is depicted in gray lines. To specify Pareto front accurately, for any stock, the λ amount is drawn in range 0.05 to 0.95 with 0.05 differences. For any value of λ, the algorithm is run with 1000 iterations and mean return and its risk is drawn. Comparing base and resulted Pareto front shows operation validity of the proposed machine in finding optimal result with various λs.
9. Conclusions
- In this paper, a new machine called spin glass automata is introduced. The machine has the properties of cellular automata as well as spin glass. In other words, this automata has property of self-organizing in specific temperature; also has local behavior that cells interact according to any defined rule (inspired by cellular automata) and also according to thermodynamic rules (inspired by spin glass). It has parallel and simultaneous processing ability and can actually solve optimization problems.Also in this paper dynamic of the machine investigated in solving optimal portfolio selection and experimental results compared and evaluated against real data with accurate result from 5 well known stock market of the world. The results show that speed and accuracy of the machine is appropriate in solving the problem and thus can be used as an optimization problem solver algorithm.In addition to mentioned experiments, SGA dynamic investigated through phase transition, entropy and correlation tests. Phase transition and entropy tests show that the machine follows thermodynamic rules. Correlation test, demonstrates ability of the machine to find global optimums. At the end, performance of the algorithm is compared to that of four famous heuristic algorithms (genetic algorithm, simulated annealing, Tabu search and neural network) in solving optimal portfolio selection problem. Also Pareto front is evaluated to show the ability of the machine to cover finding result for various risks.
Notes
- 1. Long Range Spin Glass
References
| [1] | E. Alba, "Parallel Metaheuristics: A New Class of Algorithms," A John Wiley & Sons, INC, (2005) |
| [2] | A. Adamatzky, A. Lawniczak "Theory and Applications of Cellular Automata," Luniver Press, (2008) |
| [3] | M. Vafaei Jahan, M. R Akbarzadeh-T, "From Local Search to Global Conclusions: Migrating Spin Glass-based Distributed Portfolio Selection," Journal of IEEE Transaction on Evolutionary Computation, No. 14, Issue 4, pp: 591-601, (2010) |
| [4] | P. Sarkar, "A Brief History of Cellular Automata," ACM Computing Surveys, Vol. 32, No. 1, March (2000) |
| [5] | O. Lafe, "Cellular Automata Transforms: Theory and Application in Multimedia Compression, Encryption, and Modeling," Kluwer Acadamic Publisher, (2000) |
| [6] | A. Ilachinski, "Cellular Automata A Discrete Universe," World Scientific Publishing, (2001) |
| [7] | J. L. Schiff, "Cellular Automata: A Discrete View of the World," John Wily & Sons, (2008) |
| [8] | E. Bolthausen, A. Bovier, "Spin Glasses," Springer-Verlag Berlin Heidelberg, (2007) |
| [9] | S. Galluccio, J. P. Bouchaud, M. Potters, "Rational Decisions, Random Matrices and Spin Glasses," Journal of Physica A 259 (1998) pp: 449-456 |
| [10] | S. N. Sivanandam, S. N. Deepa, "Introduction to Genetic Algorithms," Springer-Verlag Berlin Heidelberg (2008) |
| [11] | A. K. Hartmann, M. Weigt, "Phase Transitions in Combinatorial Optimization Problems, Basics, Algorithms and Statistical Mechanics," Wiley-VCH Verlag Co, (2005) |
| [12] | A. K. Hartmann, H. Rieger, "Optimization Algorithms in Physics," Wiley-VCH Verlag Co, (2002) |
| [13] | H. Umeo, S. Morishita, K. Nishinari, "Callular Automata," 8th International Conference on Cellular Automata for Research and Industry Proceeding, ACRI, Japan, (2008) |
| [14] | H. Nishimori, "Statistical Physics of Spin Glasses and Information Processing: An introduction," Clarendon press oxford, (2001) |
| [15] | H. Nishimori, "Spin Glasses and Information," Physica A 384, pp: 94-99 (2007) |
| [16] | T. Horiguchi, H. Takahashi, K. Hayashi, C. Yamaguchi, "Ising Model for Packet Routing Control," Journal of Physics Letters A 330, 192-197, (2004) |
| [17] | A. Gabor, I. Kondor, "Portfolio with Nonlinear Constraints and Spin Glasses," Physica A 274, pp: 222-228, (1999) |
| [18] | H. Ottavi and O. Parodi, "Simulation of the Ising Model by Cellular Automata," Europhysics Letters, 8(8), pp: 741-746 (1989) |
| [19] | B. Hede and H. J. Herrmann, "Fast Simulation of the Ising Model Using Cellular Automata," Journal of Physics A: Mathematical and General, Vol.24. No.12 (1991) |
| [20] | H. Markowitz, "Portfolio Selection," Journal of Finance No 7:77-91, (1952) |
| [21] | Portfolio selection benchmark data at |
| [22] | "http://people.brunel.ac.uk/~mastjjb/jeb/orlib/portinfo.html" |
| [23] | N. Boccara, "Modeling Complex Systems," Second Edition, Springer (2010) |
| [24] | B. Chopard and M. Droz, "Cellular Automata Modeling of Physical Systems," Cambridge University Press, pp:28-38 (1998) |
| [25] | Y. Bar-Yam, Yaneer, "Dynamics of Complex Systems," Addison Wesley Longman, Inc., pp: 146-180, (1997) |
| [26] | A. Fernandez, S. Gomez, "Portfolio selection using neural networks," Computers & Operations Research 34, pp: 1177-1191 (2007) |
| [27] | D. Achliptas, A. Naor, Y. Peres, "Rigorous Location of Phase Transition in Hard Optimization Problems," Nature, Vol 435, pp: 759-764, (2005) |
| [28] | D. Coppersmith, D. Gamarnik, M. Hajiaghayi, G. B. Sorkin, "Random max sat, Random max cut, and Their Phase Transitions," Journal of Random Structures and Algorithms, Volume 24 Issue 4, pp. 502 - 545, (2003) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML