1. Introduction

GNSS (Global Navigation Satellite System) has become an important technology because it certifies the presence of positions, from collected and designed items, in a global reference system (Bernabe et al., 2012). When GPS data are first used for the monitoring of vertical ground movement, the height differences between the monitoring sites, obtained by using both GPS and leveling measurements, are normally compared to realize the accuracy of height achieved by GPS (Parks and Dial, 1997; Ollikainen, 1998). Nowadays, GNSS/leveling can be considered as an alternative for practical height determination (Featherstone, et al., 1998; Erol, 2011).

Several authors have evaluated EGM96 and EGM08 in different parts of the world (e.g. Huang and Vernneau, 2009; Claessens et al., 2009; Hirt et al., 2010; Pavlis et al., 2012; Featherstone and Olliver, 2013; Odera and Fukuda, 2013; Abeho et al., 2014). Most of the comparative studies show that EGM08 has made significant improvement over EGM96. However, such studies have not been carried out in Egypt especially, northern-coastal line.

This paper carries out an initial assessment of EGM96 and EGM08 using four different methods (Bi-Linear Interpolation, Bi-Quadratic Interpolation, Triangulation, Nearest Neighbour). Refer to (http://docs.geotools.org/latest/javadocs/org/opengis/coverage/InterpolationMethod.html) for more assumptions and mathematical explanations about the used interpolation methods. These models have been compared with accurate DGPS/precise leveling derived undulations over 52 station in the Northern-Coastal line of Mediterranean Sea, Egypt.

Many researches have been carried out and discussed the geoid determination using different interpolation methods (ARANA et al., 2017; Chymyrov and Busics 2014; Janssen and Watson 2010; Lambrou 2018; Soycan 2014).

2. The Global Gravitational Models (GGMs)

The Global Gravitational Models (GGMs) are geopotential models of the Earth consisting of spherical harmonic coefficients published by the Office of Geomatics at National Geospatial-Intelligence Agency (NGA). Three models of EGM are used to calculate geoid undulation of an area. First version is EGM84 with n=m=180. Second version is EGM96 with n=m=360. Third version is EGM08 with n=m=2160. Where (n) and (m) are the degrees and orders of harmonic coefficients. The higher degrees and orders of harmonic coefficients give more parameters to the models, which lead to high precision. EGM08 also contains expansions to n=2190.

The NGA provides the model in two formats: in a raster image recording the geoid height at each coordinate at a given resolution, or in a format providing the numerical parameters – the coefficients – defining the model.

EGM96 is the result of a collaboration between the National Imagery and Mapping Agency (NIMA), the NASA Goddard Space Flight Center (GSFC), and the Ohio State University. It took advantage of new surface gravity data from many different regions of the globe, including data newly released from the NIMA archives. Major terrestrial gravity acquisitions by NIMA since 1990 include airborne gravity surveys over Greenland and parts of the Arctic and the Antarctic. These collection efforts have improved the data holdings over many of the world's land areas, including Africa, Canada, parts of South America and Africa, Southeast Asia, Eastern Europe, and the former Soviet Union. In addition, there have been major efforts to improve NIMA's existing 30' mean anomaly database through contributions over various countries in Asia. EGM96 also included altimeter-derived anomalies derived from ERS-1 by Kort & Matrikelstyrelsen (KMS), (National Survey and Cadastre, Denmark) over portions of the Arctic, and the Antarctic. The raster from EGM96 is provided at 15'x15' resolution.

The National Geospatial-Intelligence Agency (NGA) has developed the new Earth Gravitational Model EGM08, completed to degree 2160. This model, incorporates an improved version of 5' × 5' global gravity anomaly database, an improved ocean-wide set of altimetry-derived gravity anomalies, and has benefited from the latest GRACE-based satellite-only solutions (Pavlis et al., 2012). EGM08 provides an unprecedented resolution and accuracy, exposing even the smallest of incompatibility errors. The official Earth Gravitational Model EGM08 has been publicly released in 2008 as Zero Tide model. This model contains additional coefficients extending to degree 2190 and order 2159. Full access to the model’s coefficients and other descriptive files with additional details about EGM2008 are provided on web pages. All synthesis software, coefficients, and available pre-computed geoid grids assume a Tide Free system, as far as permanent tide is concerned.

3. Study Area

The study area is located in the northern Egypt from El- Salloum to El- Alameen cities, along the Mediterranean north coast “Figure 1”. It extends from longitude 25° 09' 45"E to 28° 49' 37"E, and from latitude 30° 57' 10"N to 31° 37' 07"N. The study has been carried out using 52 GPS/Leveling data points as shown in “Figure 1”. This data set comes from research project carried out by the Survey Research Institute (SRI), Egypt. The precise leveling observations were performed as closed loops, run between known high precision benchmarks established by The Egyptian Survey Authority (ESA) based on the national vertical datum of Egypt, whose origin is based on Mean Sea Level (MSL) at Alexandria tide gauge 1906. In addition, GPS measurements were carried out relative to ESA national geodetic reference framework of Egypt.

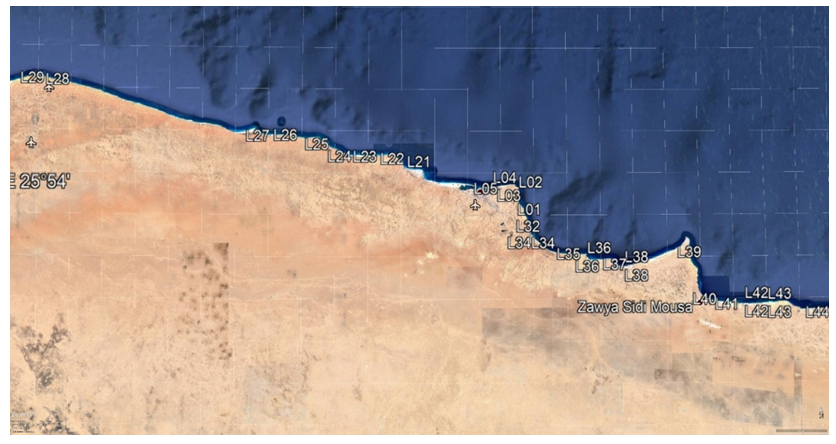Figure 1. DGPS/Precise levelling observed stations

4. Data Sets

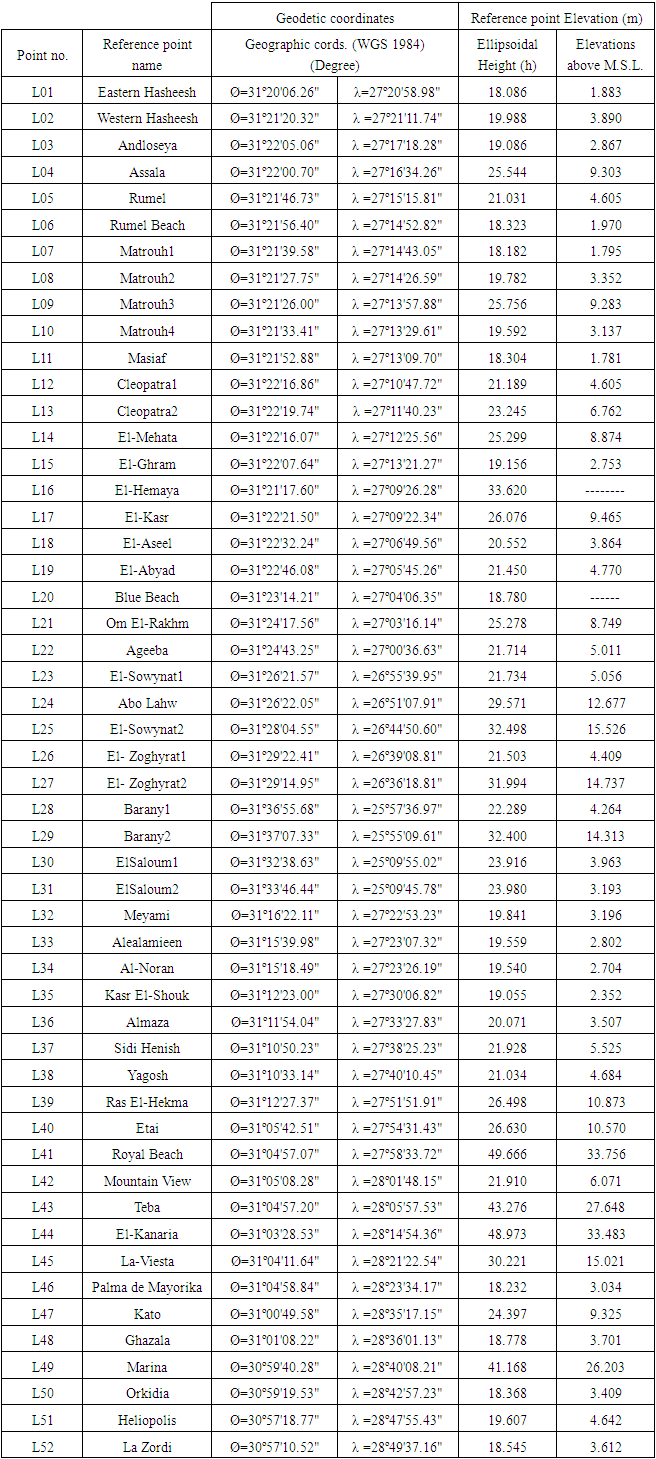
The datasets acquired for this study from station L1 to L52, see “Figures 1,2”, include: station name; projected coordinates (ETM); geographic coordinates; orthometric height (H) from precise levelling; ellipsoidal height (h) from static DGPS measurements by relative technique as shown in Table 1.

Figure 2. Station L1

Table 1. Observed DGPS/Precise Levelling data for all survey stations

“AllTrans v.3.002” EGM08 geoid calculator software developed by Hans-Gerd Duenck-Kerst, has been used to calculate geoid undulations for EGM08 model using four different methods; and for EGM96 model geoid undulations, ICGEM website has also been used.

4.1. Precise Levelling (Orthometric Height (H))

The orthometric heights are required for survey, mapping, as well as engineering/environmental projects. These heights are referred to the geoid surface which is a surface that is at all places on the surface at right angles to the gravity vector direction (Awka, et. Al. 2018).

The orthometric heights of the stations have been obtained through tying the first-order levelling loops to the national vertical datum of Egypt that is based on the mean sea level at Alexandria tide gauge of 1906.

4.2. DGPS measurements (Ellipsoidal Height (h))

The dual frequency Trimble 5700 GPS receivers were used in static mode for average 2 hours’ session, minimum elevation angle of 15 degrees, Geometric Dilution of precision of 2-4, and epoch interval of 15 seconds, see Figure. 3 for the Number of satellites covered in site fieldwork. During the field work on a primary control base reference station in relative technique mode, the base receiver was constantly logging data throughout the duration of collecting fieldwork. Online post-processing TBC planning software was used to post-process DGPS data.

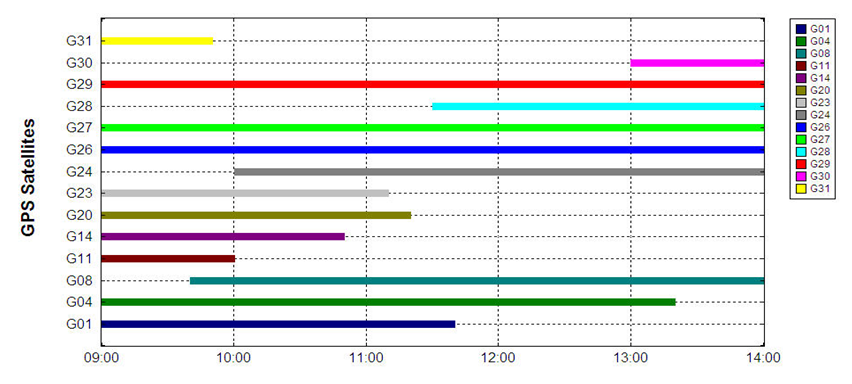Figure 3. Number of satellite covered in site fieldwork

The GPS observations for the 52 stations were taken at different times. The mission was done through many sessions; each session consists of four stations to form good baseline geometry. Therefore, the stations have been observed through these sessions during June 2013.

5. Methods

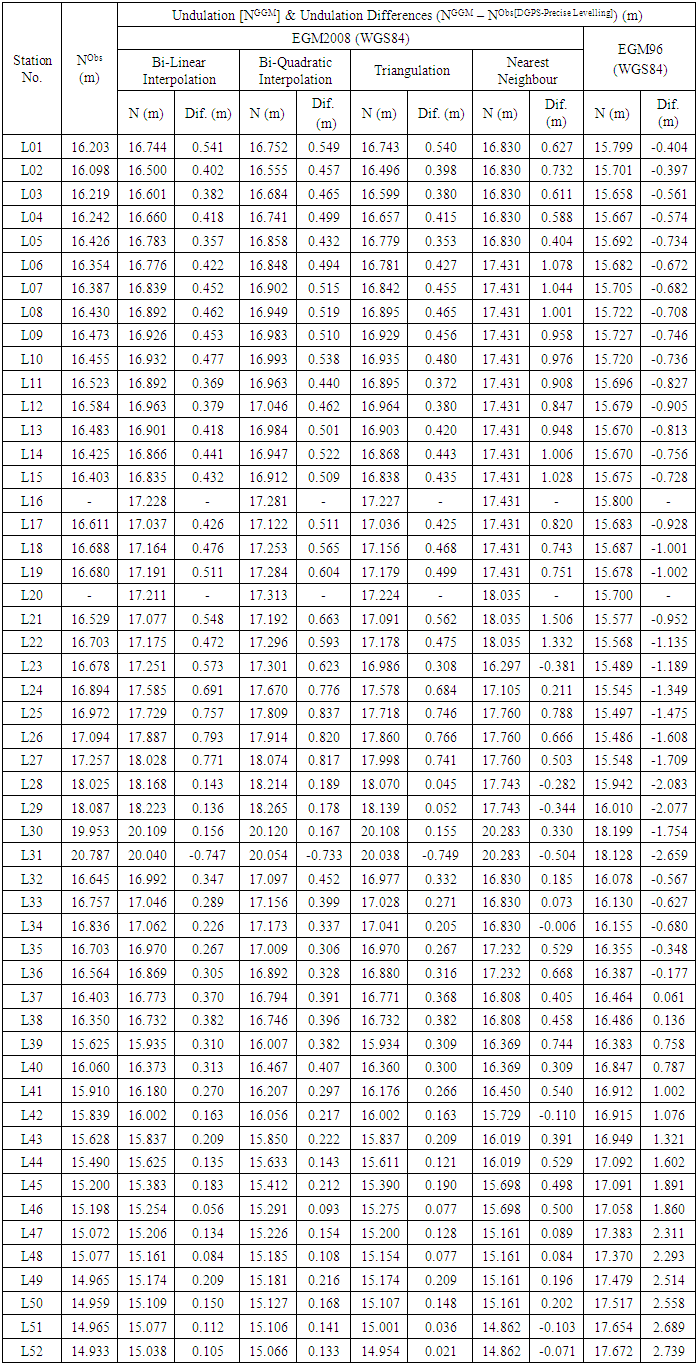
The dual frequency Trimble 5700 DGPS geodetic receivers were used in relative static mode on base reference station for a 2-hour duration of each rover observation positions. This provided the geodetic coordinates data of latitudes, longitudes and ellipsoidal heights. Online post-processing TBC planning software was used to post-process the attained data.

Using the Trimble TBC 3.2 GPS data processing package, ellipsoidal heights have been computed for each station at each session with a precision of ± 0.003 m. For each GPS station, the projected 2D coordinates (UTM east and north) have been computed at each session with a precision of ± 0.002 m.

The precise levelling data were collected by Leica NA2 precise level through tying the first-order levelling loops to the national vertical datum of Egypt. The allowable error of the precise levelling is ±3√L mm where L is the distance between each two stations in kilometre. “AllTrans v.3.002” EGM08 geoid calculator software has been used for EGM08 geoid undulations; and the International Center for Global Earth Models (ICGEM) has also been used for EGM96 geoid undulations, by min1x1 Tidefree SEL 1՝ x 1՝ database.

An initial assessment of four different methods of EGM08 (Bi-Linear Interpolation, Bi-Quadratic Interpolation, Triangulation, Nearest Neighbour). These methods have been compared with accurate DGPS/precise leveling derived undulations over 52 station in the Northern-Coastal line of Mediterranean Sea, Egypt.

6. Results

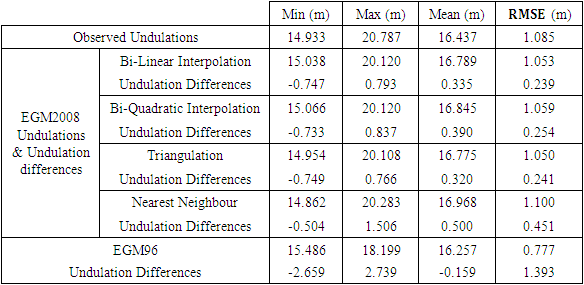
The static DGPS provided better ellipsoidal heights. It is logical that better geoidal undulation would lead to better estimates of orthometric heights (Awka, et. Al., 2018).

The differences between gravimetric and DGPS/Precise levelling geoid undulations along the Mediterranean Western Coastal Line from El- Salloum to El- Alameen, have been calculated and shown in Table 2. Statistics of the differences between gravimetric and DGPS/Precise geoid undulations are given in Table 3.

The results from this study are highlighted below:

6.1. Geoid Undulation/Height (N)

The geoid height (N), is required for the most notable and primary use of the transformation between Global Positioning System (GPS)-derived ellipsoidal heights and orthometric heights. After post-processing of the DGPS data by TBC planning software, the geoid undulation is computed from both GGMs and DGPS/levelling observed heights.

6.1.1. From GGMs

From Table 2 below, the EGM08 geoid undulations have been determined for the four studied methods. EGM08-Bi-Linear Interpolation Method is noted to be nearly consistent. In addition, the EGM96 geoid undulations have been also computed.

The calculated geoid heights obtained from the EGM08 was computed as is referred by Equation (1) (Yazid, et Al., 2016):

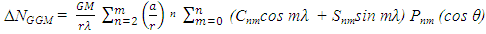(1)

Where ∆N_GGM = the geoid heights derived from the global geopotential model (GM).

GM = the product of the Earth’s mass and the gravitational constant.

r = the radial distance to the computation point, a is the semi-major axis of the reference ellipsoid.

C_nm and S_nm = fully normalized harmonic coefficients.

P_nm = the fully normalized Legendre function.

Ø & λ = the geodetic latitude and longitude of the computation point.

6.1.2. From DGPS/Levelling Observations

The measured ellipsoidal height (h) from DGPS is combined with observed orthometric (H) from precise levelling to compute geoid undulation (N), results are shown in Table 2.

The N is given by Heiskanen and Moritz (1967) and Eteje et al (2018) as:

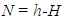(2)

6.1.3. The Geoid Undulation Differences

From computations, the differences between both GGMs and DGPS/Precise levelling derived geoid undulations are also shown in Table 2.

The differences are calculated as follows:

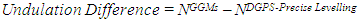(3)

Table 2. NObs & NGGMs & Undulation Differences (NGGMs – NDGPS-Precise Levelling)

7. Analysis and Discussion

Several steps have been used for comparing the geoid undulations from GGM and observations. 52 controls have been used for this study and the geoidal undulations from the two sources are shown in Table 2. This study has shown a range of differences in Table 3. were as follows; 1.540 for Bi-Linear Interpolation, 1.570m for Bi-Quadratic Interpolation, 1.515m for Triangulation, 2.010m for Nearest Neighbour and for 5.398m EGM96. The results from this study has shown a RMSE of these differences were as follows; ±0.239m for Bi-Linear Interpolation, ±0.254m for Bi-Quadratic Interpolation, ±0.241m for Triangulation, ±0.451m for Nearest Neighbour and ±1.393m for EGM96. There is a marked improvement in the overall RMSE from ±45cm (Nearest Neighbour) to ±24cm (Bi-Linear Interpolation). The smaller the range of values (between the lowest and highest N^GGMs – N^{DGPS-Precise Levelling}) the better orthometric heights obtained. In this instant, the EGM08-Bi-Linear Interpolation Model is more adequate source of orthometric height determination for topographical mapping, engineering and environmental studies and others along the Mediterranean Coastal Line.

Table 3. Statistics of NObs & NGGMs & Undulation Differences (NGGM – NDGPS/Precise Levelling)

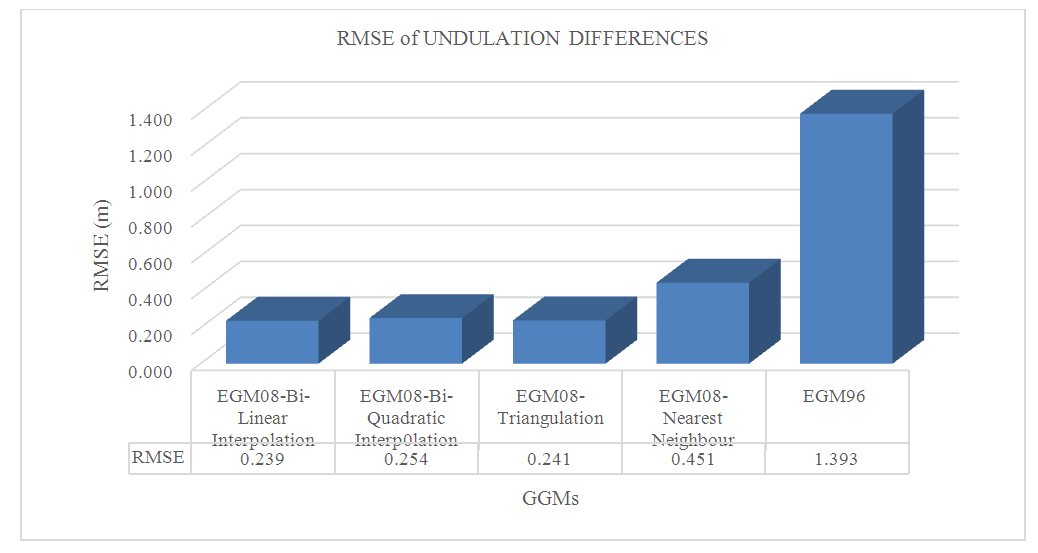Figure 4. RMSE for GGMs different Models

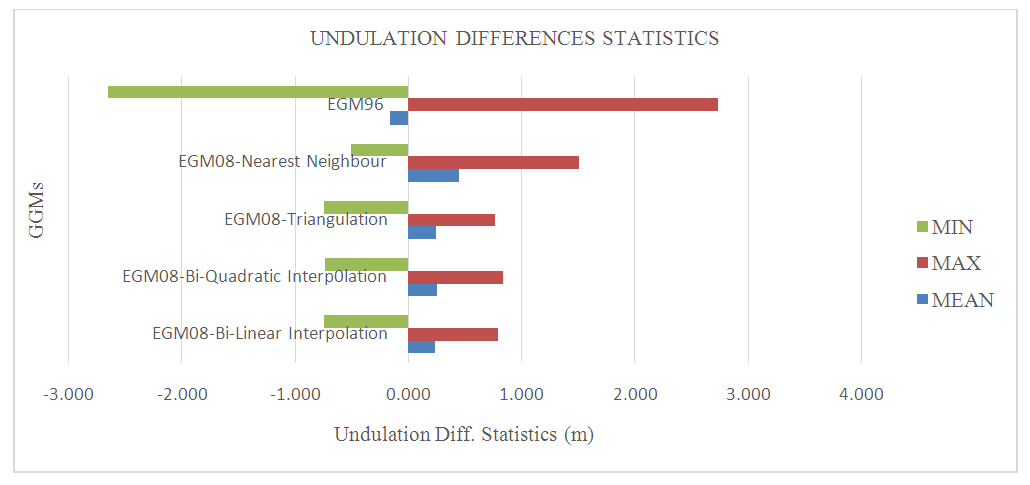Figure 5. Statistics of GGMs different Models

8. Specifications for Topographical Survey

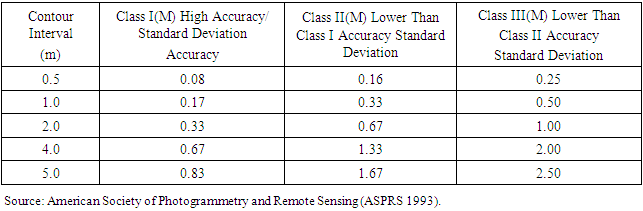
The accuracy limits for contours can be obtained from, the standard deviation of the differences compared against the specifications given by American Society of Photogrammetry and Remote Sensing (ASPRS 1993) as shown in Table 4.

Table 4. ASPRS Topographic Elevation Accuracy Requirement for Well-Defined Points

From Table 4, it is seen that the EGM08-Bi-Linear Interpolation with σ=±0.239m, checked against the specification above, can be used to produce topographical map with 2m contour interval for intermediate accurate survey, but still inadequate for survey applications where a high accuracy is required.

9. Conclusions

The release of the EGM08 GGM is a millstone step in improving geoidal modeling on a global scale. Based on several comparisons against DGPS/levelling data sets, the precision level of the EGM08 models is estimated to be ±0.239m for Bi-Linear Interpolation, ±0.254m for Bi-Quadratic Interpolation, ±0.241m for Triangulation and ±0.451m for Nearest Neighbour against ±1.393m for EGM96. There is a marked improvement in the overall RMSE of EGM08 models from ±45cm (Nearest Neighbour) to ±24cm (Bi-Linear Interpolation).

This study has also implied that use of EGM08-Bi-Linear Interpolation & EGM08-Triangulation methods is preferable to use for orthometric height determination.

It is also seen that EGM08-Bi-Linear Interpolation Model can be used to produce topographical mapping of 2m contour interval for intermediate accurate survey, but still inadequate for survey applications where a high accuracy is required. It may be encouraged to develop a geometric geoid model for local applications instead of adopting a model that is inadequate for accurate geo-data acquisitions.