-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Geographic Information System
p-ISSN: 2163-1131 e-ISSN: 2163-114X
2017; 6(4): 156-167
doi:10.5923/j.ajgis.20170604.03

Performance Evaluation of Precise Point Positioning (PPP) Using CSRS-PPP Online Service
Saad Bolbol, Amr H. Ali, Mona S. El-Sayed, M. Nasr Elbeah
Surveying Engineering Department, Faculty of Engineering Shoubra, Benha University, Cairo, Egypt
Correspondence to: Mona S. El-Sayed, Surveying Engineering Department, Faculty of Engineering Shoubra, Benha University, Cairo, Egypt.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Precise Point Positioning (PPP) of a Global Navigation Satellite System (GNSS) can be considered as an alternative solution from the differential GNSS positioning technique. Recently, PPP technique takes the spotlight due to its low cost and large number of users. Initially dual frequency PPP technique was implemented using GPS only observations. Nowadays, it has started to combine GPS+GLONASS observations in order to improve the position accuracy and reduce the convergence time. The main objective of this research is to examine the performance of the combined method compared with stand-alone GPS solution using CSRS-PPP online service processing for both static and kinematic modes. The overall results show that the GPS+GLONASS constellations does not improve the convergence time of kinematic PPP, while the static mode results of the GPS+GLONASS solution present better accuracy rather than the stand-alone GPS solution.
Keywords: GPS, GLONASS, Static, Kinematic, CSRS-PPP
Cite this paper: Saad Bolbol, Amr H. Ali, Mona S. El-Sayed, M. Nasr Elbeah, Performance Evaluation of Precise Point Positioning (PPP) Using CSRS-PPP Online Service, American Journal of Geographic Information System, Vol. 6 No. 4, 2017, pp. 156-167. doi: 10.5923/j.ajgis.20170604.03.
Article Outline
1. Introduction
- Global Navigation Satellite System (GNSS) is using GPS, GLONASS, Galileo, and Beidon in various applications such as navigation and surveying. Due to that the traditional techniques require high cost of establishing and maintaining a network of permanent stations. On the other hand, the International GNSS Service (IGS) provides highly precise satellite orbits, clock corrections or atmospheric products. This led to the new approach Precise Point Positioning (PPP) [1]. A GPS (PPP) is an absolute positioning technique for providing a high level of position accuracy in a small time using single receiver in global reference frame (ITRF) [2]. The accuracy of PPP depends on the ability of mitigating all kinds of errors. These errors can be categorized into three classes: satellite related, signal propagation related, and receiver / antenna configuration errors [3]. The convergence time depends on number of visible satellites and station specific environment conditions [4]. Precise point positioning using GPS observations achieves accuracy for static and kinematic stations at the millimeters to centimeter levels, respectively [5, 6].A PPP solution depends on GNSS satellite clock and orbit corrections coming from a network reference stations, where these corrections are calculated and sent to the user online [7]. The receiver uses these corrections to give the better positioning without referring to the base station. However, in some cases such as urban area, the number of visible GPS satellites is not sufficient for position accuracy [8]. In addition, PPP is providing centimeter level accuracy in static and kinematic modes [9]. The use of GPS and GLONASS together versus solely the GPS, improves both precision and accuracy. Also, it can provide not only the positioning in some locations where adequate GPS satellites is not available [10] but offers more visible satellites to users as well, which is expected to enhance the GDOP and the overall solution [11, 12].Whereas several GLONASS satellites were visible, an improvement in convergence time and accuracy (correlated to satellite geometry improvement) was observed [13]. Most case studies carried out concur with the above statements [14]. One observes an improvement for short sessions especially when the horizon is limited [15], allowing users to check their GPS results from a different independent system [16, 17]. Nowadays online services are very popular to users due to its easy usage, free charges, and no required licenses [18]. The online processing service of the Canadian Spatial Reference System – precise point positioning (CSRS-PPP) was used to get the coordinates through a user friendly interface [19]. The data used here is dual frequency for GPS only and GPS+GLONASS; having them both operating in static and kinematic modes where the user can get the results in ITRF reference frame. The aim of this research is to compare the PPP results using single receiver (dual frequency) for stand-alone GPS and combined GPS+GLONASS data by utilizing the CSRS-PPP online PPP service. For this purpose, two tests were done; one in static mode (urban area) and the other in kinematic mode in open area.
2. Combined GPS and GLONASS PPP Model
- The mathematical model of static and kinematic PPP is widely described in the literature, i.e.: [20, 13]. The pseudo range and carrier phase observables on GPS L1 and L2, and GLONASS G1, G2 can be expressed as follows:
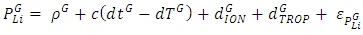 | (1) |
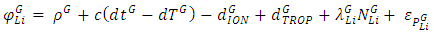 | (2) |
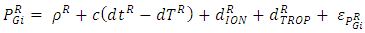 | (3) |
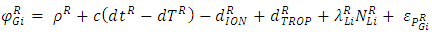 | (4) |
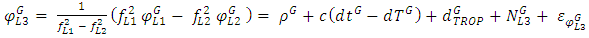 | (5) |
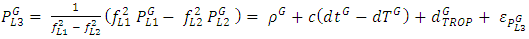 | (6) |
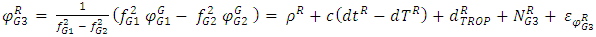 | (7) |
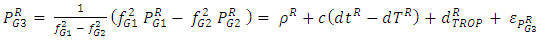 | (8) |
3. Methodology
- The proposed methodology to evaluate the performance of only GPS along with combining GPS and GLONASS observations for PPP is outlined at Figure 1. This is implemented through three main stages, data collection, data processing, and accuracy assessment.
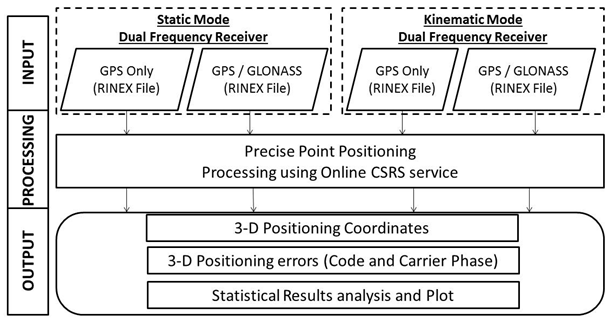 | Figure 1. Conceptual Applied Methodology |
4. The Collected Data
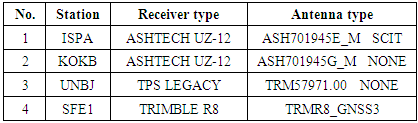
- A total of 4 reference stations were used for the analysis. For static assessment, GNSS observation datasets were collected on Wednesday, March 11, 2015 at GPS week 1835 from twelve IGS permanent stations. In addition to these sites, a local station SFE1 is established at the roof of Faculty of Engineering at Shoubra, Cairo, Egypt and continuous observations were taken from this site at the same previous time span over the GPS week 1835 (7 days of observations).Table 1 shows a list of these stations, the receiver, and antenna types. Figure 2 shows the GPS network, which is adjusted with fixing two control stations only, RAMO and DRAG. NICO station was considered as check point for results assessment. In kinematic mode, PPK continuous trajectory was collected on Wednesday, October 12, 2016 (UTC) in an open area near Cairo – Ain El Sokhna road. In order to complete the analysis, we need a reference solution to get a better results, a base station was created near the area of interest and was fixed in connection with SFE1 station (baseline for kinematic work).
|
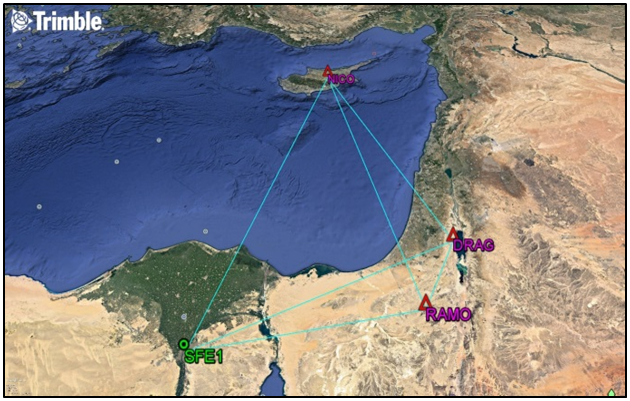 | Figure 2. Network of fixing station SFE1 with three IGS stations |
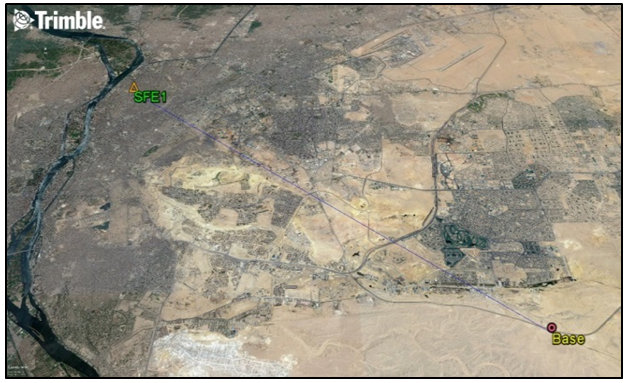 | Figure 3. Baseline between SFE1 and base station for kinematic work |
5. Results and Discussion
- To analyze the results of GPS and the combined GPS/GLONASS PPP, two static solutions and another two kinematic solutions are assessed.
5.1. Assessment of Static PPP
- Final precise products throughout dual frequency observations are used to analyze the results from static PPP technique. The assessment of static PPP will depend on the accuracy and the convergence time of the solution.Two factors are affecting the GPS processing results. The first one is the satellite geometry (DOP) which indicates the status of satellite distribution at the time of observation. The second is the satellites number in view during observation process. Figure 4 shows the number of satellites used in the data processing for three IGS stations and station SFE1.
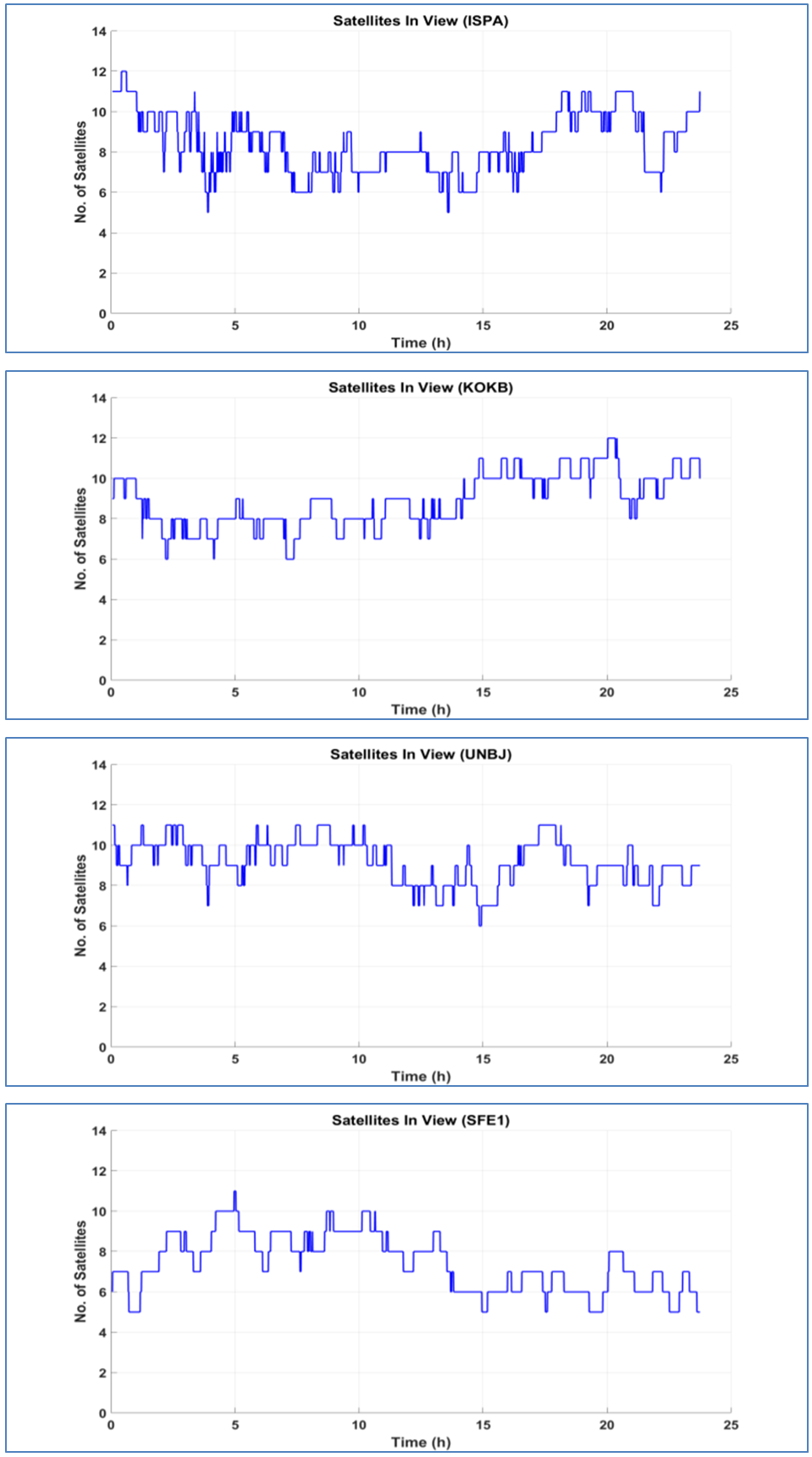 | Figure 4. Number of satellites in view for stations ISPA, KOKB, UNBJ and SFE1 |
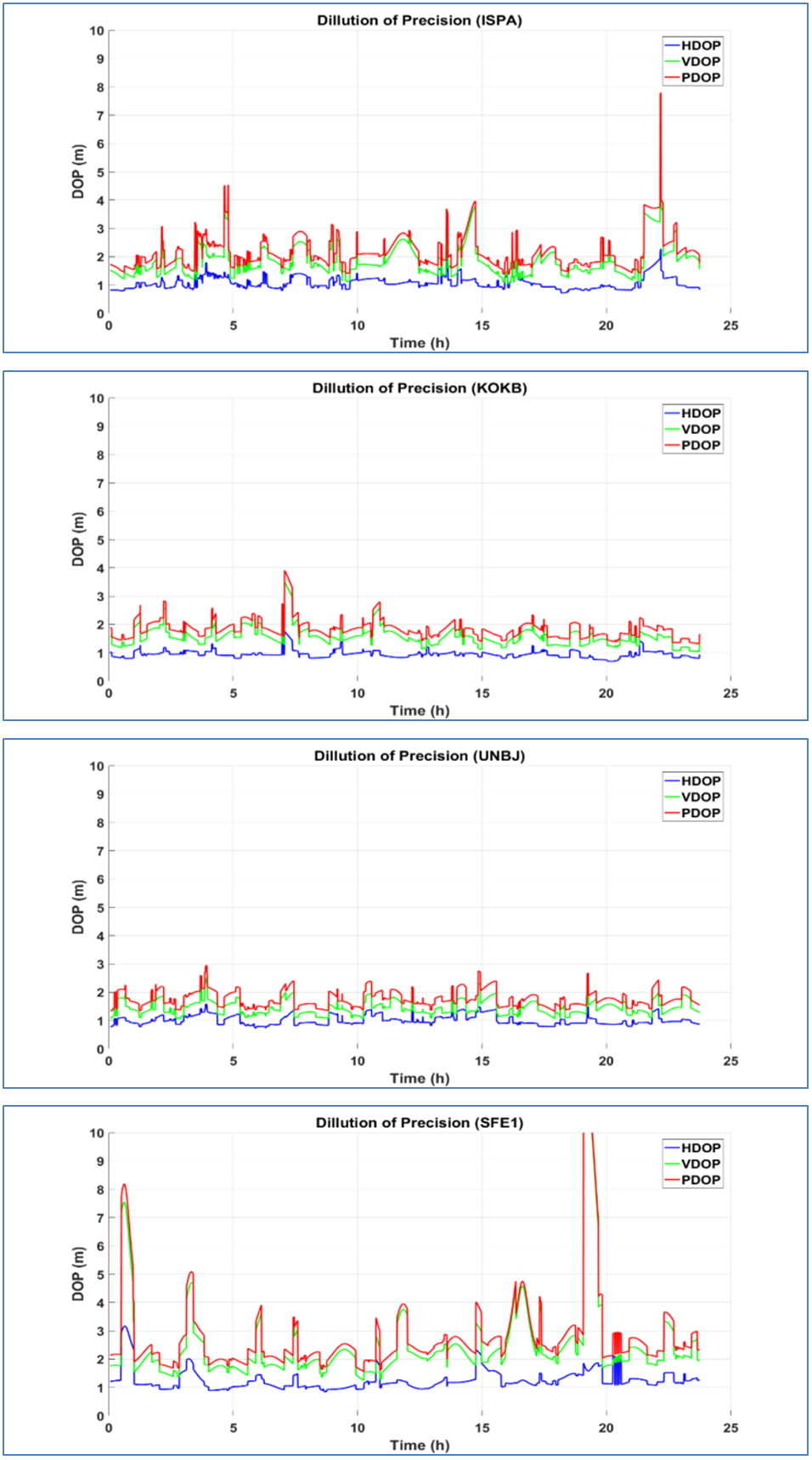 | Figure 5. Satellite geometry (DOP) for stations ISPA, KOKB, UNBJ and SFE1 |
5.1.1. Stand-alone GPS
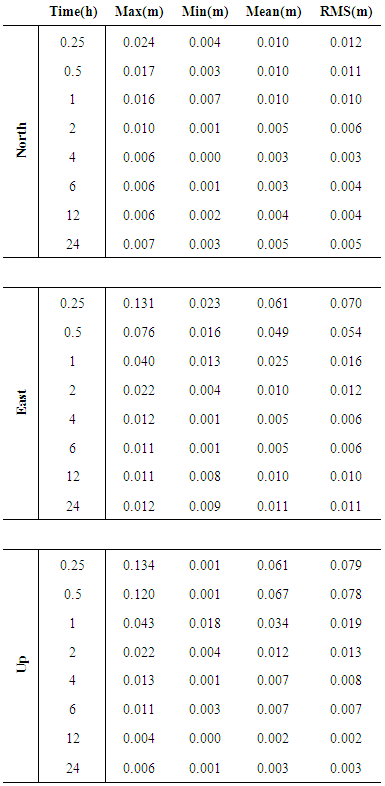
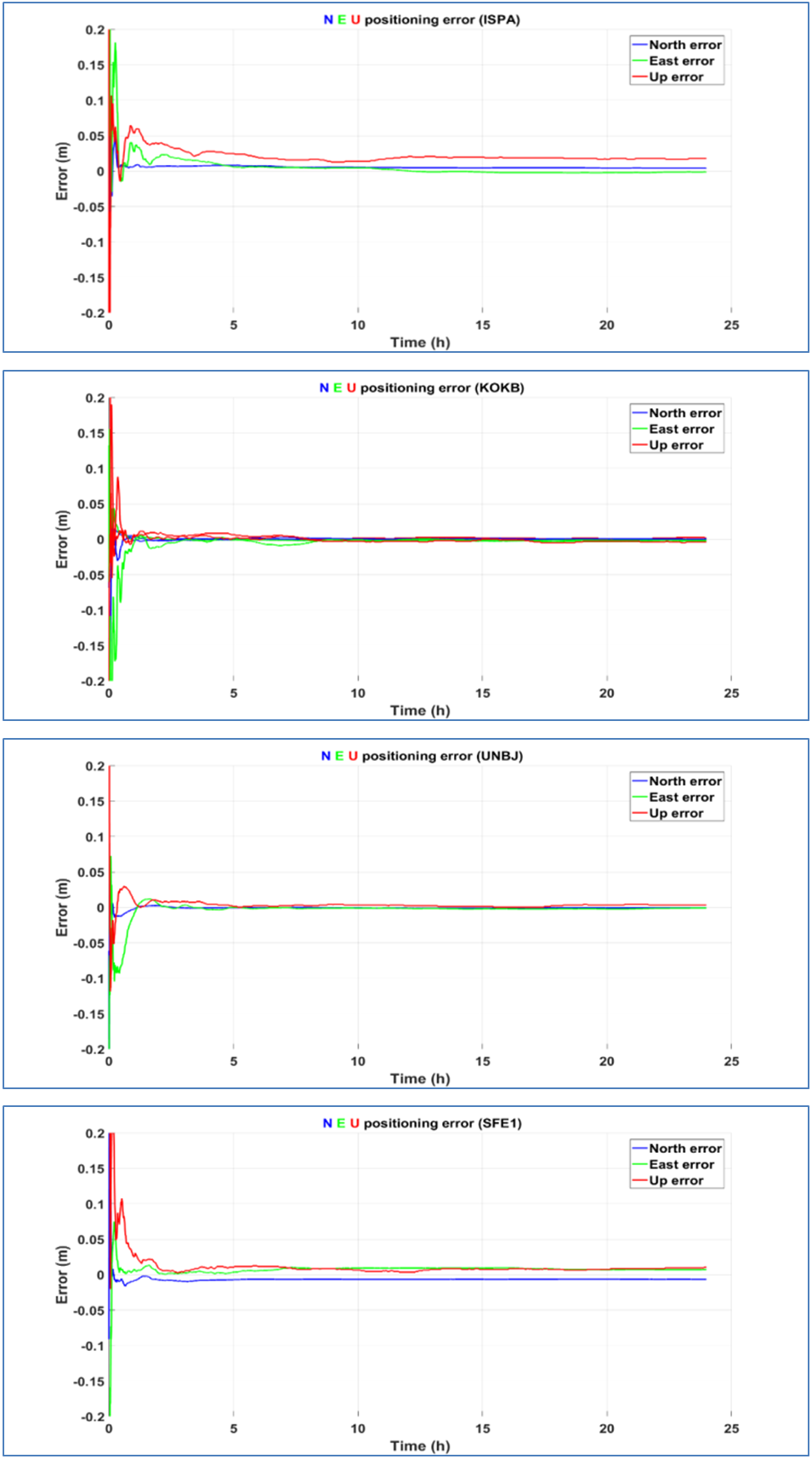
- Figure 6 shows the processing results of four stations ISPA, KOKB, UNBJ and SFE1 using dual frequency stand-alone GPS observations and final precise ephemeris; including the positioning errors in east, north and up directions with respect to the true coordinates. These figures illustrate the accuracy of CSRS-PPP solutions over the day.
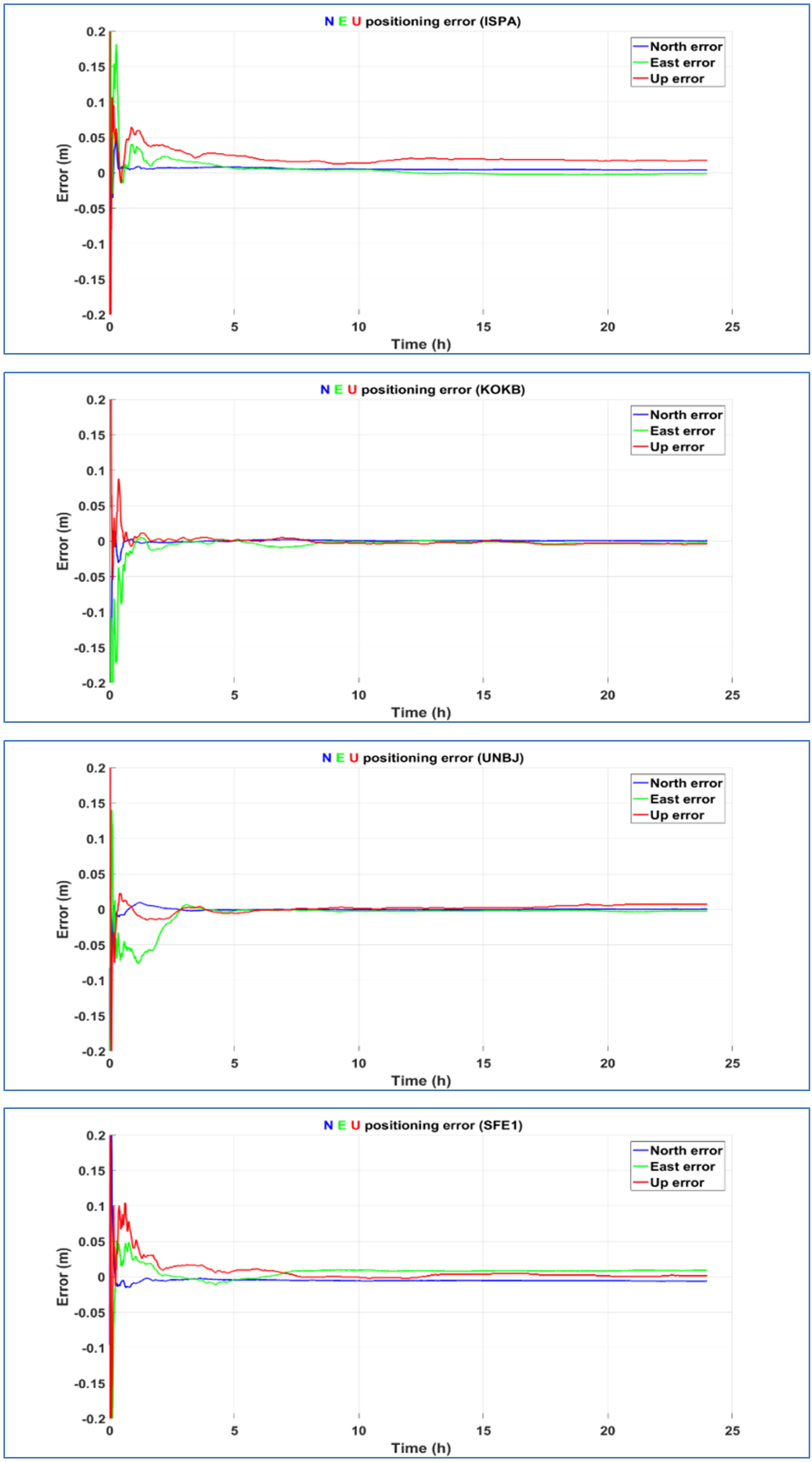 | Figure 6. Positioning errors for stand-alone GPS observations in static solution |
|
5.1.2. GPS + GLONASS
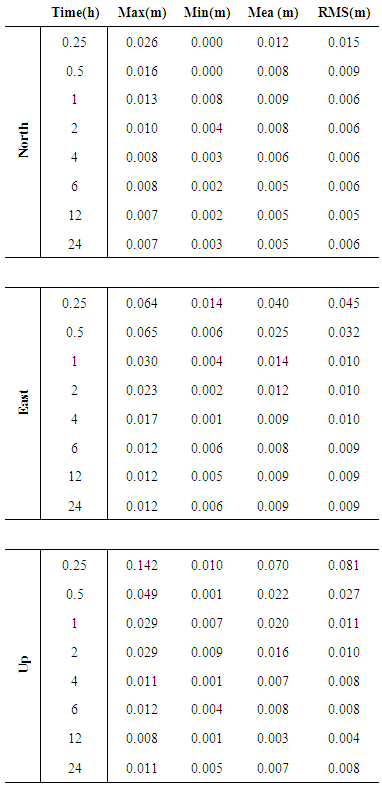
- Figure 7 illustrates the processing results of four stations ISPA, KOKB, UNBJ and SFE1 using dual frequency GPS+GLONASS observations and final precise ephemeris, including the positioning errors in east, north and up directions with respect to the true coordinates.
 | Figure 7. Positioning errors for GPS+GLONASS observations in static solution |
|
5.2. Assessment of Kinematic PPP
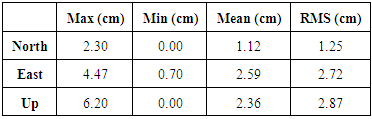
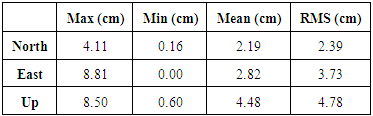
- In addition, the CSRS-PPP solution with stand-alone GPS and GPS+GLONASS will be assessed. Fixed coordinates of PPK test were obtained from relative solution of base and rover receiver observations using Trimble Business Center software, where these coordinates were used as true coordinates to assess the accuracy of PPP solution. The conversion of 3D station coordinate estimates from PPP solution allowed the positioning of differences in north, east, and up components with respect to the true coordinates.
 | Figure 8. Image for the observed continuous kinematic trajectory |
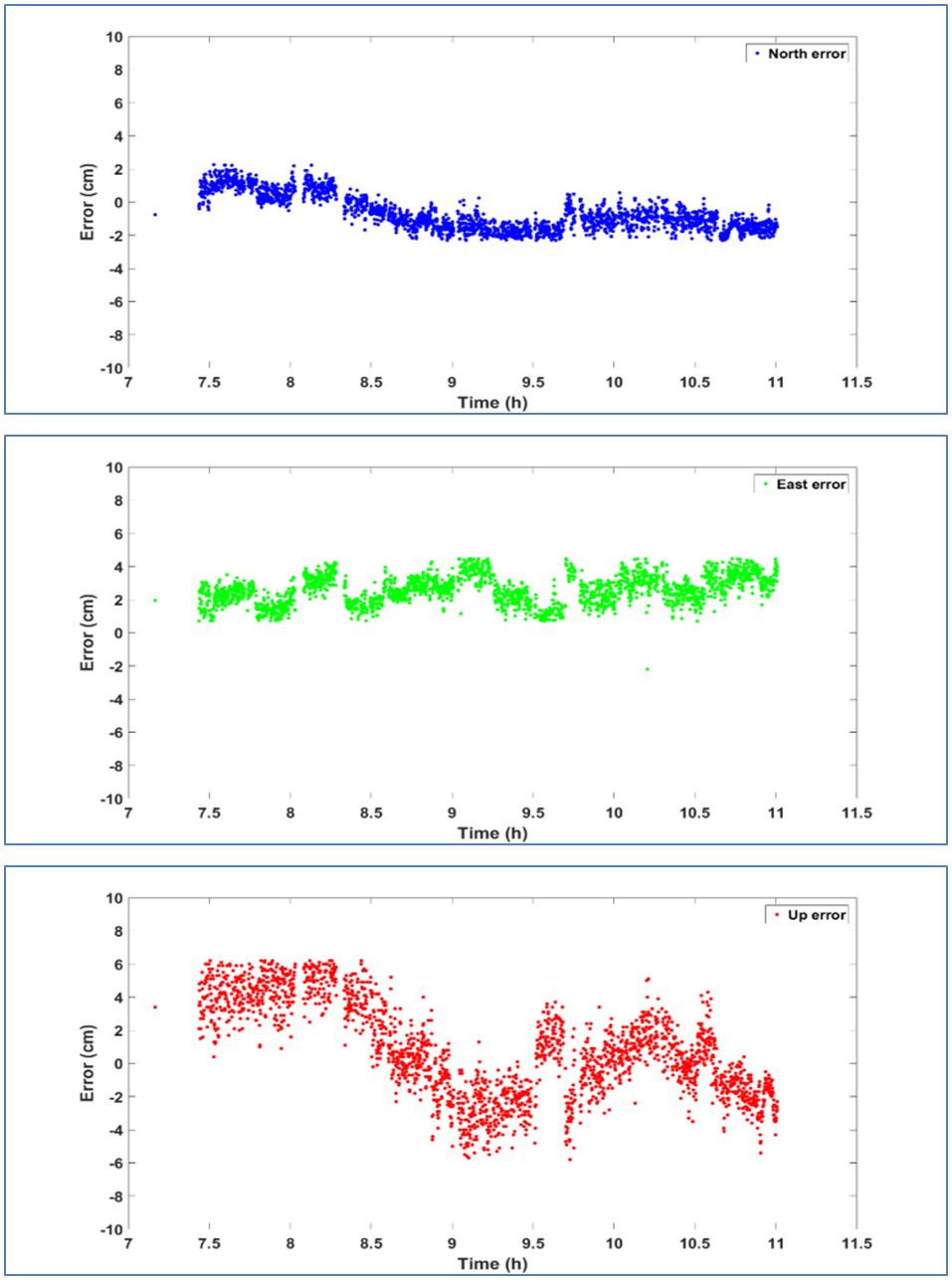 | Figure 9. Positioning errors for GPS-Only observations in kinematic solutions |
|
|
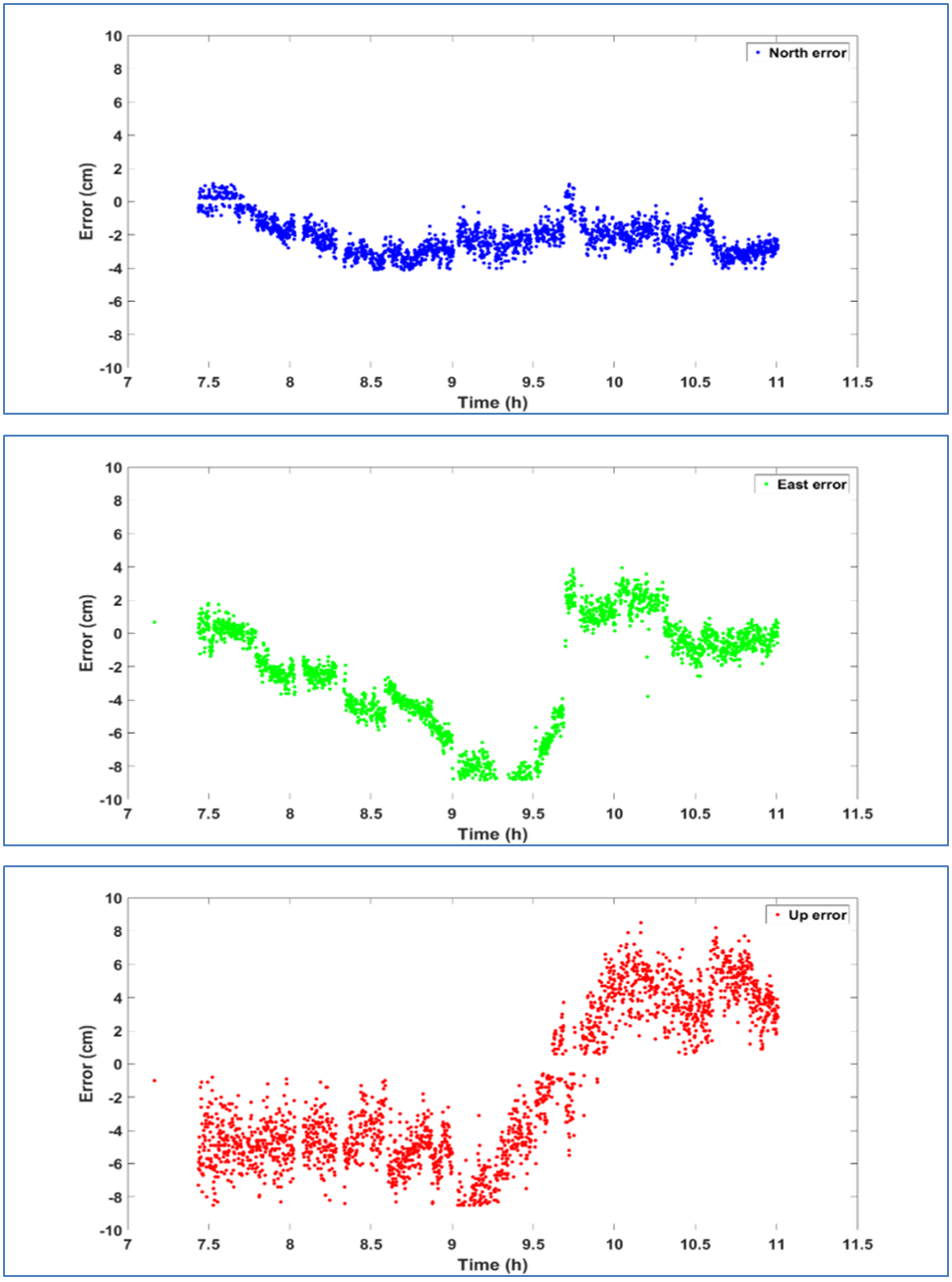 | Figure 10. Positioning errors for GPS+GLONASS observations in kinematic solutions |
6. Conclusions
- In this research, absolute and relative methods of positioning, PPP and DGNSS respectively were related. PPP as an absolute method for positioning can be beneficial for its application in geosciences. The cost of preplanning, logistics and personnel are lower in comparison to differential solution. Satellites are considered to be the direct homogenous and consistent reference system for PPP with a satellite-geometry-depending quality (in addition to station specific environment). This enables applications in areas where no reference stations are established, unlike the DGNSS that is categorized as a relative technique that relies on the distribution of reference station network. In this research, we analyzed the accuracy of the position determination using single receiver GNSS observations, including the analysis of result difference between stand-alone GPS and combined GPS+GLONNASS observations in static and kinematic modes. Based on the results presented in this research, the combined GPS+GLONASS–PPP configurations show evident improvement in comparison to stand-alone GPS in terms of solution availability and accuracy in static mode. For the stand-alone GPS, the RMS error is calculated and it was found 1cm, 1.6 cm and 1.9 cm for north, east and height (up), respectively, after one hour. As for the GPS + GLONASS, the RMS error became 6 mm, 1 cm and 1.1 cm for north, east and height (up), respectively. With the addition of GLONASS constellation, it allows more precise results in urban areas since the satellite signal is partially obstructed in the stand-alone GPS mode. In the kinematic mode, the accuracy of the results in the case of using GPS+GLONASS solution was not better than the corresponding solution of stand-alone GPS since the RMS was 1.2, 2.7 and 2.8 cm for north, east and height (up), respectively, in the stand-alone GPS. After adding the GLONASS constellation, the RMS became 2.3, 3.7 and 4.7 cm in north, east and height (up) respectively. Based on these results, GPS & GLONASS observations in PPP are of immense importance in processing short-static sessions conducted under conditions of limited satellite availability.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML