1. Introduction

Nowadays, technologies that extract human movement trajectories from various moving object tracking systems are becoming powerful and the amount of trajectory data is increasing rapidly. Trajectory data can be directly collected with various location-aware devices such as GPS, cellphones (González et al. 2008), WiFi instruments (Torrens 2008) and Bluetooth devices (Eagle and Pentland 2006). Trajectories can also be indirectly extracted from video cameras (Nguyen et al. 2005) or manually recorded using TabletPC (Torrens et al. 2011). Moreover, trajectory data can be reconstructed from some location proxies of physical movement (e.g. using geo-tagged digital photos to reconstruct people’s travel paths). By analyzing very large amounts of trajectory data, scientists can successfully classify trajectories based on different human behavioral types (Dodge et al. 2009), predict the behavioral type of unknown trajectories and detect abnormal behavior (Makris and Ellis 2002) or critical crowd situations (Johansson et al. 2008).

Trajectory classification that can detect the type of movement or behavior (e.g. driving, running or walking) associated with unknown trajectories, is important for deriving knowledge and patterns of movement from trajectory data (Giannotti and Pedreschi 2008). It plays an important role in many applications of trajectory data analysis and mining. For example, it can be used to detect abnormal pedestrian behavior in pedestrian video surveillance systems (Niu et al. 2004), abnormally moving vehicles in traffic video surveillance systems (Fu et al. 2005), vessel types for fishery control, pollution control and border control from satellite images (Lee et al. 2008), and the theft of mobile devices (Yazji et al. 2011). The main task of trajectory classification is to use existing knowledge about the movement behavior to train a model or classifier. Examples of classifiers include the distance/similarity-based model (Lin and Shim 1995, Froehilch and Krumm 2008, Buchin et al. 2011), decision-tree model (Fu et al. 2005), the hidden Markov model (HMM) (Nguyen et al. 2005, Khokhar et al. 2007), and the Support Vector Machine (SVM) (Niu et al. 2004, Dodge et al. 2009). Such classifiers serve as an explanatory tool for distinguishing trajectories of different activity types and for predicting, which specific behavior type of any input trajectory data belongs to what predefined categories of behavior.

In general, existing methods can be categorized into two types based on what features of trajectory data are extracted and used to build the classification model: trajectory classification based on (1) geometric shape and (2) movement parameters. The geometric shape approach directly manipulates the spatial characteristics to classify trajectories into one of several predefined categories with similar geometric properties (see chapter 10 in Giannotti and Pedreschi 2007). It is suitable for abnormal behavioral detection from trajectories that were generated by similar moving objects (e.g. trajectories of vehicle in traffic surveillance analysis). However, this type of classification method is limited to the spatial context where all trajectories should be compared in the same geographic region since all predefined trajectory categories are tied to this region. Besides, temporal information has usually been ignored when treating trajectories as two-dimensional line segments since comparing three-dimensional space-time trajectories is computational expensive.

The other type of trajectory classification is based on movement parameters, which are usually descriptive statistics that were extracted from trajectory data to discriminate the differences between movements. Several movement parameters, such as moving speed, turning angles, acceleration etc., have been used in current research as movement features in trajectory classification. Since these movement parameters are not correlated with specific geometric characteristics of trajectories, this type of approach can be applied to any trajectory data regardless of its spatial context. However, the accuracy of classification depends heavily on selecting appropriate movement features from trajectories. With normal movement parameters it is difficult to fully distinguish the differences in movement, especially for similar moving objects. For example, people could run as fast as a slow cyclist (same speed) in the same street (same turning angle). Recent research extracts local movement profiles, such as the amplitude and frequency of movement parameters over time, as new features to discriminate different types of movement in trajectory classification. However, few try to combine geometric features and movement parameters to classify trajectories.

To overcome these research challenges, this research develops an efficient approach to automatically —and with relatively high accuracy— detect the movement type of unknown objects from trajectories. This approach extends the movement parameters trajectory classification by introducing two new types of complexity measures as new features to classify movement. Specifically, one type of complexity measure is geometric complexity measured by the Fractal Dimensions of trajectories, and the other is structural complexity measured by Approximate Entropy (ApEn) of the variation in movement parameters. This research suggests that ApEn, which provides complexity information about the subtle changes that occur in the structure of sequential movement parameters of trajectories, and Fractal Dimensions, which provide the overall description of geometric complexity, can be used to deal with trajectories with any length and improve the accuracy in trajectory classification. This proposed approach will benefit research of trajectory data analysis and mining, such as video surveillance, traffic management and location-based services, by improving the quality of trajectory classification.

To demonstrate the utility of this approach, 800 GPS traces that have been shared and manually tagged with a specific movement type by Internet users on the website Openstreemap.org were collected as experimental data. Experiments are conducted to test the feasibility of the two types of movement features introduced in this essay: complexity measures of movement parameters and complexity measures of geometric. The performance and accuracy of these trajectory classification models, one with and one without complexity features, are analyzed and then compared using a confusion matrix and receiver operating characteristics (ROC). The overall 85.4% average accuracy of prediction demonstrates the applicability of the proposed method for detecting the movement type of raw trajectory data.

This paper is organized as follows: the complexity of movement is introduced in section 2 by focusing on two types of complexity measures of movement: Fractal Dimension and ApEn. Section 3 describes the methodology of trajectory classification in this research. In section 4, two experiments are conducted to validate the performance trajectory classification model. The results are compared to evaluate the effects of the two proposed complexity based movement features. Section 5 presents a brief summary and future research opportunities.

2. Complexity of Movement

A trajectory is a path of connected geometric line segments that can be treated as a type of time series data. Many existing methods in computational geometry and time series analysis have been borrowed for trajectory analysis and classification. For example, several geometry-based approaches are developed to compare geometric similarities between trajectories, as well as time series analysis approaches are borrowed to compare similarities between time series extracted from trajectory. However, to the best of author’s knowledge, none of the existing research introduces complexity measures, which have been widely studied in fractal theory (Batty 1985) and time series research (Feldman and Crutchfield 1998) to describe the characteristics of movement for trajectory classification. This research seeks to demonstrate that complexity measures of trajectories can provide new and discriminative features of movement for trajectory classification. Specifically, this research introduces two types of complexity measures for trajectories: a geometric complexity measure using Fractal Dimensions and a structural complexity measure of movement parameters using ApEn.

2.1. Geometric Complexity of Movement and Fractal Dimension

When trajectories are visually plotted in two-dimensional space (see Figure 1), the fundamental feature of trajectories is their geometric shape. Much existing research focuses on directly comparing the geometric shape between trajectories to identify similar movements with several limitations. In fact, the geometric shape of a trajectory itself can tell us the characteristics of movement via its geometric complexity measure. For example, people walking through a crowded street block may generate a trajectory full of angles and turns by avoiding collisions or visiting random places, while a car drives through the same street will create a straight trajectory. The geometric complexity of these two movement trajectories is significantly different: the trajectory of pedestrians in a crowded environment is more complex geometrically than the trajectory of vehicles. This research argues that such geometric complexity of trajectories can be used as a discriminative feature to describe movement.

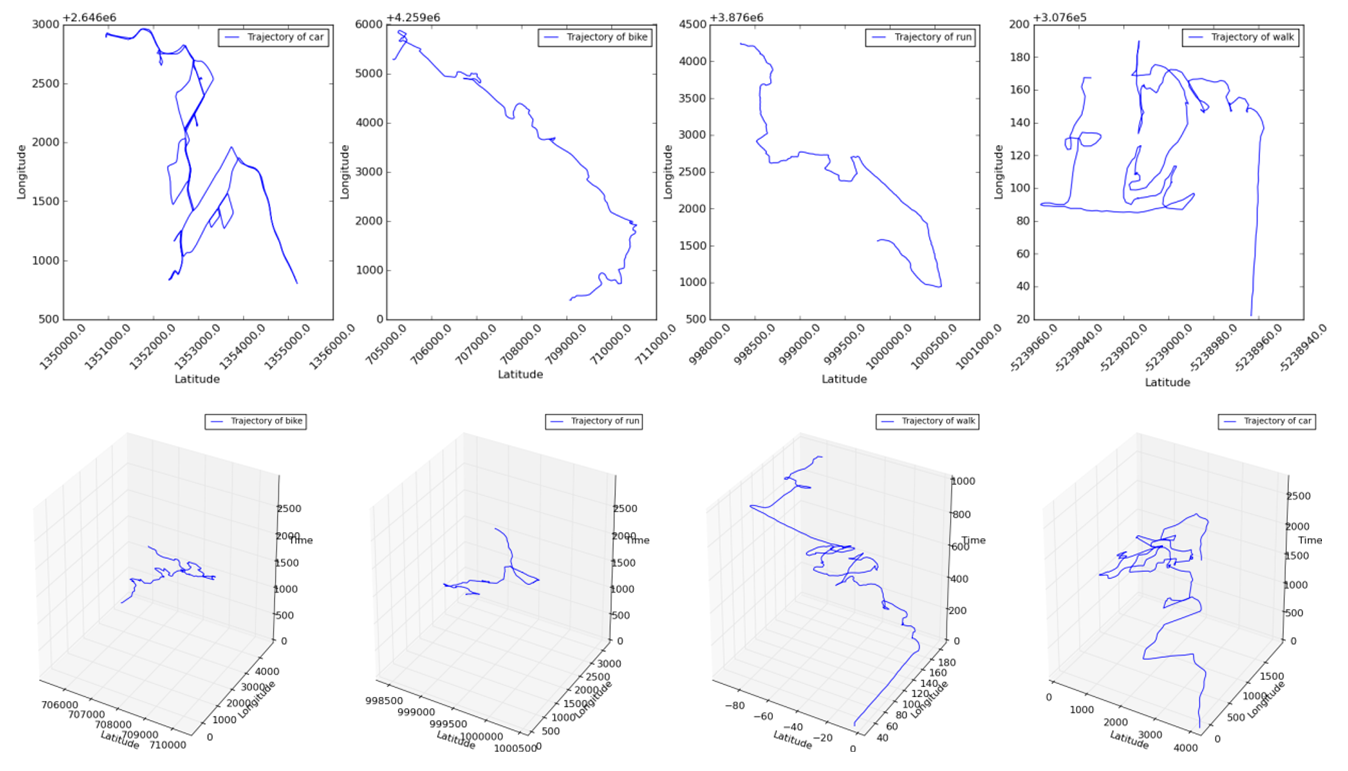Figure 1. 4 different randomly selected GPS trajectories (car, bike, run, walk) in 2D (upper) and in 3D (lower, with vertical axis representing time)

To measure the geometric complexity of trajectories, this research introduces the Fractal Dimension as a geometric complexity-based feature for trajectory classification. Fractal dimension is used to measure the tortuosity of two-dimensional trajectories (Mandelbrot 1967, Nams 2005). It has been used to analyze the trajectories of animals to study their movement patterns and habits (Fritz et al. 2003) and to analyze the structure of trajectories of pedestrians (Nara and Torrens 2007) to compare the visual similarity between trajectories (Torrens et al. 2011). The FD value of a trajectory ranges from 1, which refers to a straight line, to 2, which means a trajectory whose tortuosity occupies a whole plane. It is derived from the linear relationship between the logarithm of total distance (D) and the logarithm of the inverse of the currently employed measuring scale (S) based on the knowledge that the total length is highly dependent on the scale adopted (Nams 2005), as follows:

(1)

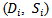where n represents the number of different scales employed to calculate the total distance of a trajectory. A regression model can be constructed from the pairs, and the FD value is then calculated as (1 +α). One problem that may impact the precision of the FD value is a possible underestimation or truncation of the path length through different measuring scales. For the purpose of improving precision, Nams (2005) proposed a FMean method that computes an FD value twice by starting to measure total distance from two ends of a trajectory whereby the mean FD value is used as FMean. In this research, FMean will be used as a movement feature that describes the geometric complexity of trajectories.

2.2. Structual Complexity of Movement Parameters and Approximate Entropy

Besides the geometrical shape, the global characteristics of trajectories can be described through some movement parameters, such as average velocity, acceleration, turning angle, straightness index etc. These descriptors, at a given scale, can differentiate a variety of behaviors. For example, in most cases, people are running with higher moving speed than walking; driving a car will be associated with a much higher acceleration than riding a bike; the turning angle of a vehicle will be smaller than that of a pedestrian. These differences can be seen in Table 1, where the basic descriptive statistics of several global movement parameters were computed empirically from four different types of movement trajectories (walk, run, ride bicycle and drive car) that are randomly selected from experimental data (see Section 4). However, in some cases these descriptive statistics would not be accurate: some people might run very slowly while others might walk very fast; or in a race, a bicycle could reach a fairly high speed that is faster than a slowly driven car. Therefore, additional features that can distinguish different movement parameters of trajectories are needed for a successful classification task.

By plotting the sequential data of these movement parameters (velocity, acceleration and turning angle) against time, we can see that obvious structural differences of different types of movement exist: different behavior exhibits different amplitude and frequency variations of its movement parameters along the time axis (see Figure 2). In this example, for a velocity-time sequence, running behavior has the relatively highest frequency and median amplitude; walking behavior exhibits the relatively median frequency and lowest amplitude; driving a car is associated with the relatively lowest frequency and highest amplitude; and riding a bike has the relatively median frequency and amplitude. Many approaches to analyzing movement were designed to quantitatively and statistically analyze these time-series data by checking the shifts in mean levels, variability, and the autocorrelation structure. For example, Nams (1996) proposed VFractal to measure the fractal dimension of the turning angles series to evaluate the self-similarity (autocorrelation) of movement. Dodge et al. (2009) measured the deviation and sinuosity of these sequential movement parameters and categorized them into four predefined low-high deviation-sinuosity groups as the local movement features for trajectory classification. However, such methods that only take into account the aggregate amount of randomness of the serial data may ignore the subtle changes that happened in the structure of sequential data (Pincus 2008).

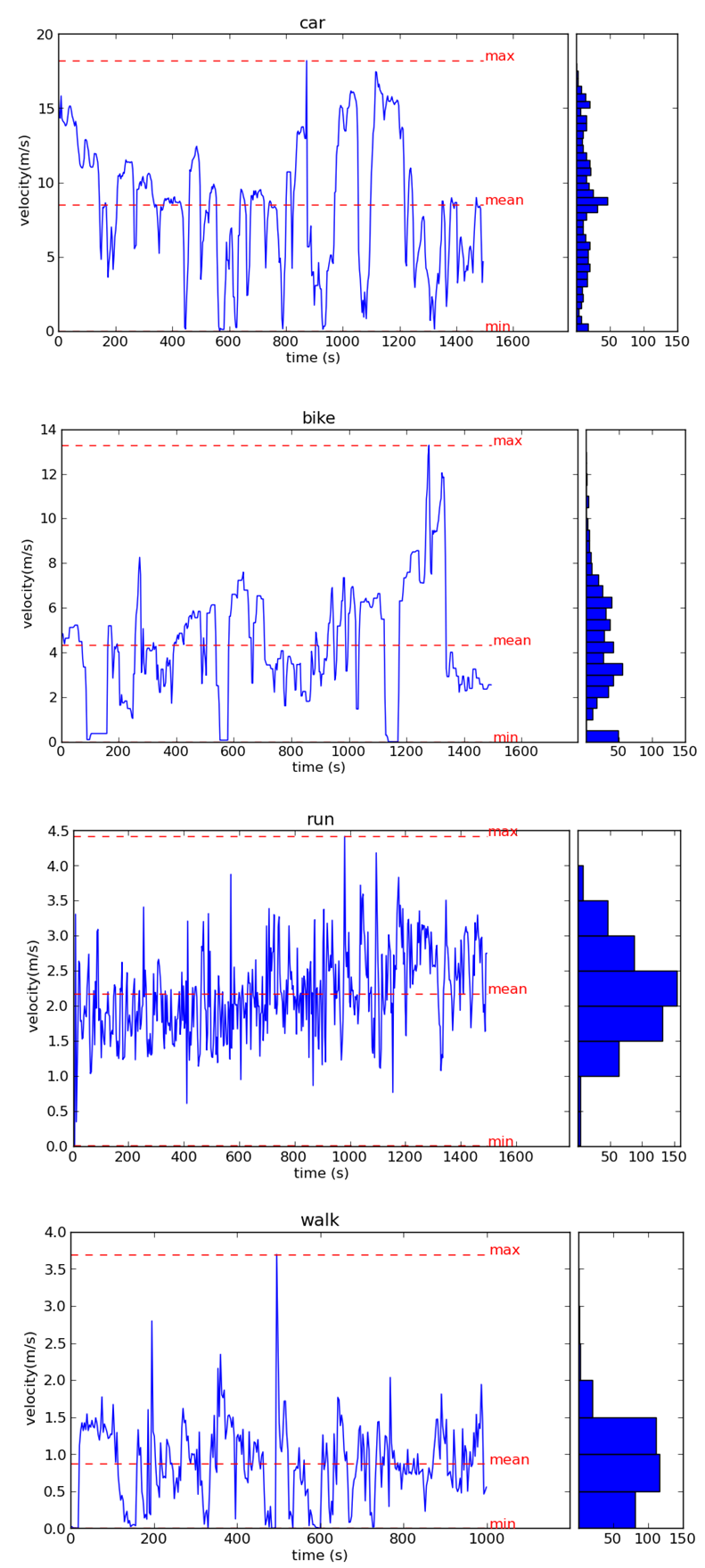Figure 2. Plots of velocity against time for: car, bike, run, and walk (from top to bottom) of 4 randomly selected trajectories with 4 different movement types

To address this problem, trajectories were treated as time series data and the structural complexity measurement ApEn was introduced as a measure of irregularity of sequential data in time series analysis. ApEn is rooted in information entropy developed by (Shannon 1948). It is used to quantify the concept of changing complexity, and it has been widely applied in time series data analysis in finance, biology, complexity, and other fields (Pincus 2008, Pincus 1991). The ApEn value varies inversely with complex and irregularity of sequential data. It measures if a structure or pattern of change exists in sequential data. A higher ApEn value suggests that the sequential data is a random series, while a smaller value implies less complexity and more regularity (predictable pattern) in the sequential data. Therefore, this research applies the ApEn to measure the structure of sequential data with local movement parameters.

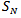ApEn values reflect the likelihood of how often “similar” patterns of observations exist in time series data. Sequential data that contains many repetitive patterns (e.g. highly structural and less informative) have a relatively small ApEn value, while a less predictable process (e.g. with complex or random structure) has a higher ApEn value. Given time sequence data , which has N continuous observations, this research denotes a subsequence of m observations at location 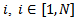, is a pattern 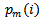. If the difference between two patterns 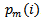and 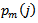is less than a predefined criterion r, we can conclude that these two patterns are similar. The approximate entropy value 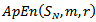can be computed with the following equation¹:

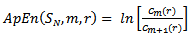(2)

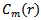where m specifies the pattern length, r defines the criterion of similarity between patterns, and is the prevalence of repetitive patterns of length m in 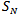, which can be computed as:

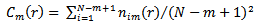(3)

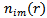where is the frequency count of patterns in 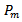that are similar to 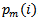. For a fixed number of N observations, large m will generate fewer patterns to measure the ApEn value than small m. As noted by the author of ApEn in (Pincus 1991), a small m (especially m=2) can distinguish a wide variety of systems, such as deterministic systems, chaotic system stochastic and mixed system, with relatively fewer points. For similarity criterion r, smaller r usually leads poor conditional probability with more similar patterns been identified, while larger r usually ignore detailed system information with less patterns been detected. As suggested by author in (Pincus 1991), choices of r ranging from 0.1 to 0.2 standard deviation of the sequence data 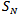can avoid a significant contribution from noise in an ApEn calculation.

3. Methods

This research develops a trajectory classification method based on two new movement feature sets that represent a trajectory’s geometric complexity and structural complexity of movement parameters. First, all trajectory data will be preprocessed by removing noise and outliers and resampling with a uniform time interval. Then, general movement features (e.g. velocity, turning angle, acceleration and straightness) and complexity-based movement features are extracted from trajectories (e.g. fractal dimension measure (FMean), and ApEn measures with regard to general movement features). Correlation analysis is then applied to study potential interrelationships between movement features. To reduce the dimensions of movement feature space, principle component analysis (PCA) is used to select a subset of uncorrelated features as principal components. The features and corresponding movement types are then used to train a classifier for trajectory classification. Different classifiers have been compared and the one with highest accuracy is selected to use. This classifier can be used to predict the movement type of an unknown trajectory.

3.1. Data Preprocessing

Before data preprocessing, this research establishes some definitions for trajectory data that can be recorded through location-aware devices (e.g. GPS) at a certain sampling interval or instantaneously through user intervention: a trajectory is the path of a moving object and it can be composed of a set of quasi-linear segments where the points 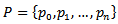are attributed spatial and temporal information, e.g. 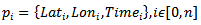. Based on this, a trajectory can be represented as follows:

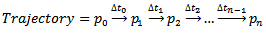(4)

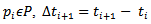where and 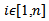. The total cost in time is 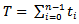and the approximate total length of the trajectory is

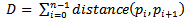(5)

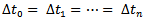If , this trajectory has a fixed sampling interval.

Usually, real-world trajectory data may not have been recorded at the same sampling rate and there may be some noise, such as incorrect locations that were recorded when location-aware devices (e.g. GPS) lost signals or were impacted by ionospheric and tropospheric errors in the trajectory data (Hoffmann-Wellenhof et al. 2001). The different sampling rate should be standardized for generating comparable Fractal Dimension and ApEn values. First, all trajectories that were recorded using latitude and longitude are simply transformed to a planar coordinate system with meters as the unit. To preprocess trajectories to contain the same fixed sampling interval, a linear interpolation approach is applied to resample trajectories at a fixed time interval. To check the noise in trajectory data, a simple rule that “moving velocity at each original point on the trajectory should be less than a predefined maximum velocity” is applied in the resample stage. The noise point will be simply removed once detected before resampling. If more than 10 noise points are detected, this trajectory will be ignored.

3.2. Feature Extraction and Selection

In the movement feature set, classic general descriptive statistics of movement parameters, which include the mean, standard deviation and skewness of moving speed, acceleration, turning angle and straightness index, are extracted from trajectories as basic movement features. At each sampling point 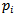along trajectory 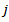with total n sampling points, these movement parameters can be calculated as follows:

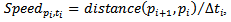(6)

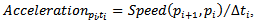(7)

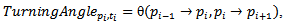(8)

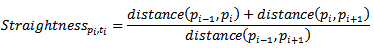(9)

Instant moving speed is calculated as the rate of location change from the previous time step. Acceleration is calculated as the rate of speed change from the previous time step. Turning angle is calculated as the direction of the movement with regard to the previous and next time steps (see Figure 3). The straightness index is calculated as the ratio of the length of two consecutive trajectory segments and the displacement from an overall start point to end point of these two segments.

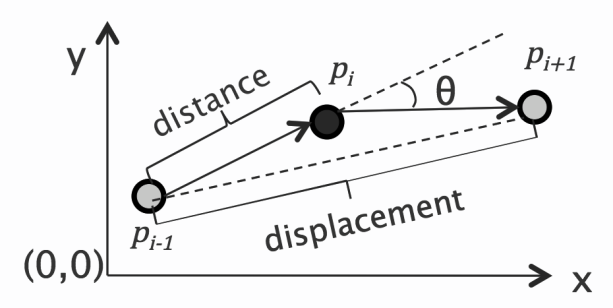Figure 3. Illustration of computing general movement parameters such as: moving speed, turning angle, displacement etc

To test the potential interrelationships between movement parameters, the Spearman correlation coefficient and the p-value for testing non-correlation are adopted. The main reason of selecting Spearman correlation is because it does not assume a normal distribution of the variables. It is a nonparametric measure of the linear relationship between two variables, and can be used to test the direction and strength of the relationship between variables (Chatfield 2004).

The new type of movement feature is the complexity measure of a trajectory. This research introduces geometric complexity of a trajectory and structural complexity of movement parameters of a trajectory. The FMean value is calculated to describe the geometric complexity of a trajectory. ApEn is calculated for each movement parameter (e.g. speed, turning angle, acceleration and straightness) to describe how the structural complexity of movement parameter varies over time. To capture all subtle changes that occurred in the structure of sequential data, the ApEn value of each movement parameter is measured at every sample point beginning from a½ trajectory. To calculate ApEn values that can distinguish different movement types significantly, the parameters of ApEn are defined as m=2 and r=0.2* standard_devation () following by the explanation in section 2.2. Then, the mean, standard deviation and skewness of ApEn values are adopted as movement features.

Then, a traditional and efficient approach, PCA is employed to reduce the dimensions of feature space by using an orthogonal transformation to reduce a set of possible correlated features to a smaller set of values of uncorrelated synthetic features (Smith 2002).

3.3. Classification Model

After the process of dimension reduction, the final feature set and movement type of trajectories will be used for trajectory classification. Then, a cross-model comparison using different classification models, such as SVM, decision tree, KNN, linear model, naïve Bayes and GMM, is applied to select a suitable classification model. As a result in experiments (see Section 4), this research selects the SVM as the classifier for trajectory classification since it achieves the highest accuracy in prediction test and has been successfully applied in many applications. SVM is robust for high-dimensional and linearly or non-linearly separable data. It finds maximal margin hyperplanes as decision boundaries to separate input features with different class labels in a multidimensional space. A subset of the training data, the support vectors is used to represent such decision boundaries. For non-linearly separable data, SVM applies a set of kernels, such as linear, polynomial, radial basis function (RBF) and sigmoid kernels, to mathematically map input features to a linearly separable space.

3.4. Trajectory Classification, Prediction and Evaluation

Trajectory classification task in this research is focusing on predicting the movement type (class label) of unknown trajectories. If there are only two predefined movement types that need to be detected, such as walk vs. run, the corresponding classification model is called a binary classifier. When there are more than two movement types in classification, the corresponding classification model is called a multi-class classifier or multinomial classifier. There are some feasible solutions that apply binary classifiers to solve this k-classes classification problem, such as a “one-against-one” or “one-against-rest” strategy. This research uses the “one-against-rest” strategy, in which k binary classifiers will be trained first and then work together as a multi-class classifier. The unknown trajectory will be classified k times using these k classifiers and generate k probability values to indicate whether or not it belongs to each one of k movement types. The movement type with the highest classification probability will be assigned to the unknown trajectory.

To avoid the over-fitting problem and improve the estimation of the classification performance, a k-fold cross-validation is applied to evaluate the classifier. This method divides the sample data into k equal-sized groups, from which one group of samples is chosen for testing and the rest of the data are used for training at each run. Then, the overall error equals the sum of errors for all k runs.

To evaluate the performance of the classification model, this research uses classification performance metrics such as accuracy and error rate (the ratio of the number of wrong predictions to the total number of predictions). Further, a receiver operating characteristic (ROC) curve is used to display the trade off between true positive rate (TPR equals the ratio of the number of true positive cases to the sum of true and false positive cases) and false positive rate (FPR equals the ratio of the number of false positive cases to the sum of true and false positive cases) (Hanley and McNeil 1983). The area under the ROC curve (AUC) can be used to evaluate if the model is accurate (with an AUC value close to 1) or inaccurate (with an AUC value close to 0.5), or compare which model performs well (with a large AUC value).

4. Experiments and Results

4.1. Data Collection

In the experiment, this research retrieved 7,010 GPS tracks that were shared by 478 Internet users in GPS exchange format (GPX) from the website Openstreetmap.org. GPX is an open file format that uses the XML schema to describe waypoints, tracks and routes. Usually, when Internet users upload and share their GPS tracks on a website, most of them also tag their GPS traces with some text descriptions, such as the movement type, date or other relevant information about the GPS traces. These meta-data were also collected with the GPX data at the same time. By using these metadata, this research develops a software program to extract trajectory samples that have metadata matches four predefined movement categories. The GPS traces, which were tagged with more than one movement type (e.g. GPS trace of commuting or traveling usually contains walking and driving car), will be ignored. This program also detects and deletes invalid trajectory data, such as empty GPX files or too short GPS traces (less than 5 minutes). After cleaning the data, 400 valid trajectories were randomly selected so that each movement category contains 100 trajectories. These trajectories will further be used as training and testing data in the experiments.

The main purpose of the experiments is to build a classifier from already known trajectory data to predict movement types of unknown trajectories from four predefined movement categories: walk, run, ride bicycle (bike) and drive vehicle (car).

4.2. Data Preprocessing, Feature Extraction and Selection

In the data preprocessing stage, outliers in each trajectory, such as points with zero latitude and zero longitude or with moving speed larger than 100 meters per second were removed. Each trajectory is then re-sampled at a fixed time interval (3 seconds) through a linear interpolation approach. As proposed in section 3.2, the movement features include (1) general features such as the mean, standard deviation and skewness of movement parameters (speed, acceleration, turning angle and straightness index) and (2) complexity features such as the FMean measure of trajectories, and (3) the mean, standard deviation and skewness of ApEn measures of the variation of movement parameters. The descriptive statistics of movement parameters of four movement types are calculated from sample trajectories and are shown in Table 1 and Table 2.

Table 1. Descriptive Statistics and Structural Complexity Measures of 4 movement parameters (Speed (a), Acceleration(b), Turning Angle(c), Straightness(d)) for 4 Randomly Selected Trajectories (Car, Bike, Run, Walk)

Table 2. Geometric Complexity Measures (Fractal Dimensions) of 4 Randomly Selected Trajectories with 4 Different Movement Types (Car, Bike, Run, Walk) Car Bike Run Walk FMean of Fractal Dimensions 1.089 1.083 1.076 1.122

The results of Spearman correlation coefficient are computed to examine the potential interrelationships between movement parameters in Table 3. From the results, we can see that there is a slight positive correlation between “speed” and “acceleration” in two movement types (“car” and “bike”). Therefore, all four movement parameters will be kept for the next stage.

Table 3. Correlation Coefficients between Movement Parameters of 4 Movement Types Correlation Car Bike Run Walk Speed-Acceleration 0.576 0.406 0.254 0.056 Speed-TurningAngle 0.128 0.098 0.068 -0.216 Speed-Straightness -0.108 -0.169 -0.196 -0.447 Acceleration-TurningAngle 0.082 0.120 0.063 -0.099 Acceleration-Straightness 0.090 -0.033 0.055 0.008 TurningAngle-Straightness -0.133 -0.354 -0.021 -0.083

After the correlation analysis, a total of 25 movement features are derived from each trajectory: 12 general movement features (mean, standard deviation and skewness of speed, turning angle, acceleration and straightness index) and 13 complexity movement features (FMean of trajectory, mean, standard deviation and skewness of the ApEn measure of speed, turning angle, acceleration and straightness index curves). Then PCA is applied for dimensional reduction of the above movement features by transforming input features to uncorrelated linear combinations. As a result, the original feature set is reduced to 10 principal components, which together contribute 90% of the original information. The new feature set is then used for the final trajectory classification.

4.3. Experiments

In this research, two experiments are designed to evaluate the trajectory classification task. In the first experiment, all proposed movement features are used to build a classifier. In the second experiment, all but the complexity features are used to build another classifier. The same sample data from the data preprocessing stage are used to extract features, and to train and test the classification model in both experiments. The performance results of two experiments are compared and analyzed in the next section.

The “one-against-rest” strategy is used to build a multiclass classifier based on binary classifiers: four binary classifiers are built and each executes a binary classification of one movement type against the rest. They work together to compose a multi-class classifier by assigning the label of the highest prediction probability classifier to the unknown trajectory. For better classification performance, a 5-fold cross-validation approach is applied to evaluate all classifiers. As a result, in each run, 80% (320 trajectories) of preprocessed data are used to train this multi-class classifier, and 20% (80 trajectories) data are used for testing.

To select a suitable classification model in the experiments, different classification models, which include C-SVM (model parameters can be seen in next paragraph), Nu-SVM (kernel=radial basis function (RBF), nu=0.5, gamma=0.25, tolerance=0.0001, cost parameter=200), KNN classification model (k=15 and Euclidean distance as weight), Logistic regression linear classification model (C=1e4, intercept scaling=2, penalty=12, tolerance=0.0001), Gaussian naïve Bayes model and GMM(alpha=0.1, number iterations=20, number components=4, threshold=0.01), are applied and compared to select the one with best performance. The parameters of each model are chosen by sweeping all possible parameter sets to find best fit. The results of cross-model comparisons of classification using dataset in first experiment are shown in Table 4. According to the results, this research employs the C-SVM, which achieves the highest prediction precision compared to four other classification models, to fulfill this classification task.

Table 4. Cross-model Comparisons of Classification Models Using Experiment 1 Dataset: 320 Training Data/80 Testing Data Precision Recall f1 score C-SVM (RBF) 0.85 0.88 0.87 Nu-SVM (RBF) 0.83 0.82 0.82 KNN 0.71 0.71 0.71 Linear model (Logistic) 0.73 0.72 0.72 Naïve Bayes (Gaussian) 0.68 0.68 0.68 GMM 0.57 0.56 0.56

According to the form of the error function, there are two types of classification SVM: one is classification SVM Type 1 (C-SVM) and the other is classification SVM Type 2 (Nu-SVM) (Chang et al. 2001). Since C-SVM produces slightly higher prediction precision than Nu-SVM, the C-SVM is adopted empirically in both experiments. The parameters of this classifier are utilized automatically by sweeping all parameters within the valid range. Both experiments generate highest precision using the RBF kernel. In the first experiment, the cost parameter is 128.0, complexity bound is 0.6, tolerance is 0.5 and numeric precision is 0.001. In the second experiment, the cost parameter is 32.0, complexity bound is 0.5, tolerance is 0.5 and numeric precision is 0.001.

4.4. Results

The results of the multi-class classification in the first experiment are shown in the confusion matrix in Table 5. As a result, the overall accuracy of prediction is about 85.4%, which is a relative good prediction result in multi-class trajectory classification outperforms much existing work. Each entry in this matrix represents the proportion of true prediction. From the results, we can see that if the movement type of input trajectory is “car”, there is a 94.12% chance that the classifier assigns the correct label. The movement type “walk” also has high prediction accuracy (94.12%). The movement type “run” has the lowest prediction accuracy (72.92%). There is 18.75% chance to incorrectly predict it as “bike” and a 6.25% chance to incorrectly recognize it as “car”. The movement type “bike” also has a relative low accuracy (79.59%). Almost all movement types could be misclassified vis-a-vis the rest types, except that there is no misclassification of “car” to “run”. Such misclassifications require further investigation to improve the accuracy of the classification.

In experiment 2, the overall prediction accuracy is 78.39%, which is lower than the overall accuracy of the classifier in experiment 1. This means that introducing the complexity measures of movement as features for trajectory classification can improve the overall prediction accuracy of the classification model. Specifically, the prediction accuracy has significant improvement in movement type “walk” (94.12% versus 88.24%), “run” (94.12% versus 80.39%) and “bike” (79.59% versus 61.22%) (see Table 6). The ROC curves and AUC values of the two experiments also supports this conclusion (see Table 7 and Figure 4): the average AUC value of experiment 1is higher than experiment 2 (0.917 versus 0.885), which demonstrates the good performance of the proposed classification model. The details of model comparison can be examined in the ROC curves and AUC values comparison of “one-against-rest” binary classification tests in Figure 4. The comparison results show that the complexity measures of movement can be used to discriminate different types of movement and used as important features of movement to improve the accuracy of classification model.

It is also interesting to note that the prediction rate of “run” in experiment 2 is higher (83.33%) than in experiment 1 (72.92%). This means that incorporating complexity measures of movement has a negative effect on distinguishing “run” from other movement types. Further investigations are required to explain this underperformance. Considering that the differences are misclassified as “bike”, it may be because complexity measures cannot discriminate “bike” and “run”.

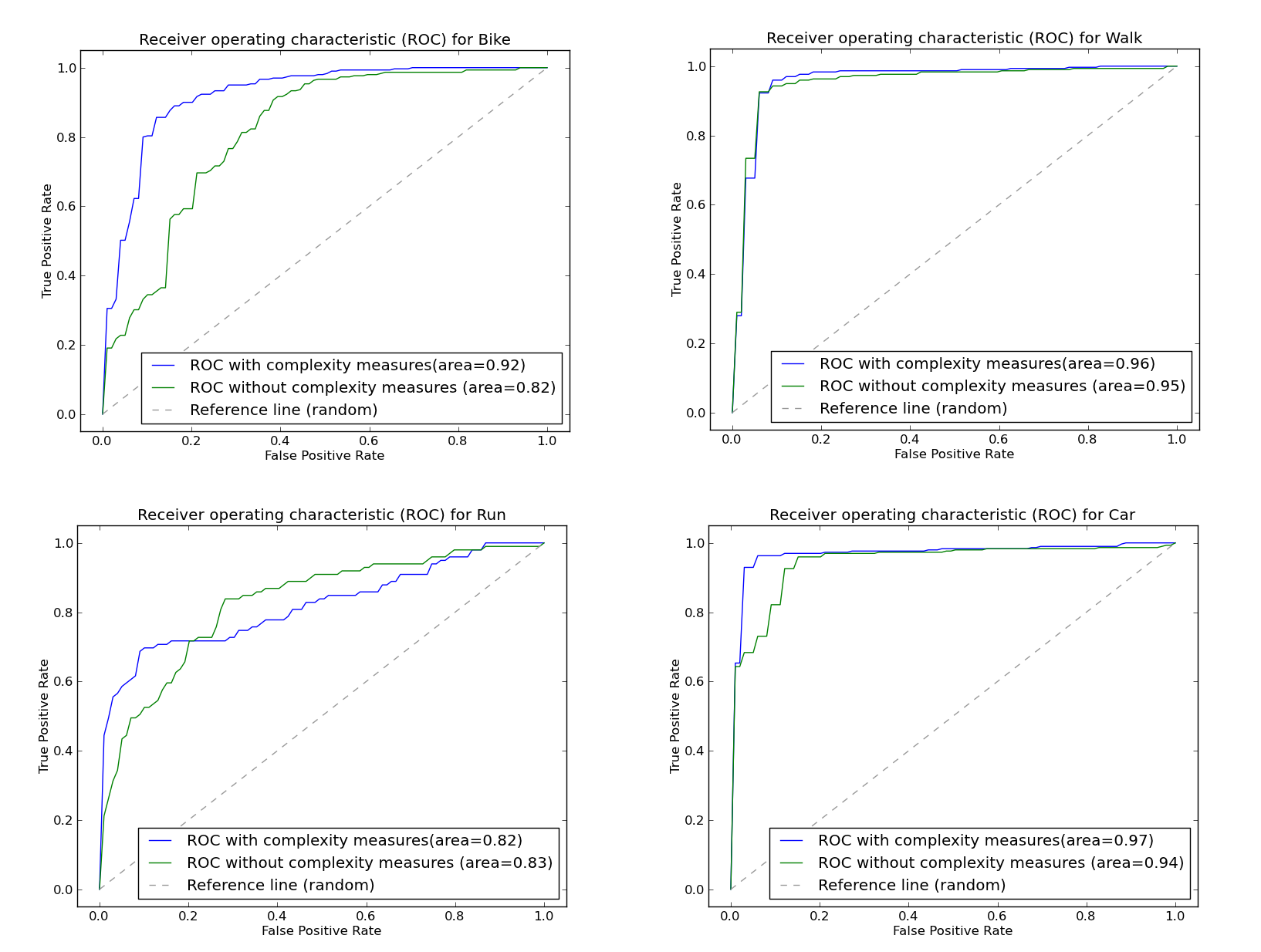Figure 4. Receiver operating characteristic (ROC) and area under ROC curves comparison of “one-against-rest” binary classification results of Bike, Walk, Run and Car in experiment 1 and 2

Table 5. Confusion Matrix of Accuracy for 4-class Trajectory Classification Problem in Experiment 1 (with Complexity Measures as Movement Features) Predicted Class Bike Car Run Walk Actual Class Bike 79.59% 10.20% 4.08% 6.12% Car 1.96% 94.12% 0.00% 3.92% Run 18.75% 6.25% 72.92% 2.08% Walk 1.96% 1.96% 1.96% 94.12%

Table 6. Confusion Matrix of Accuracy for 4-class Trajectory Classification Problem in Experiment 2 (without Complexity Measures as Movement Features) Predicted Class Bike Car Run Walk Actual Class Bike 61.22% 4.08% 22.45% 12.24% Car 5.88% 80.39% 9.80% 3.92% Run 4.17% 6.25% 83.33% 6.25% Walk 1.96% 1.96% 7.84% 88.24%

Table 7. Comparison of Classification Results of Experiment 1 and 2 Overall Accuracy Overall Error Rate AUC (average) Experiment 1 85.42% 14.58% 0.917 Experiment 2 78.39% 21.61% 0.885

5. Conclusions

This research presented a classification model based on effect movement parameters for automatically detecting movement types with unknown trajectories. To overcome some of the problems with the current approach based on movement parameters, this research introduced the geometric complexity measures of trajectories and structural complexity measures of movement parameters as two new types of movement features for trajectory classification. These two types of complexity measures actually highlight both general geometric characteristics and the subtle changes of movement parameters that exist in different moving trajectories in a classification model. The results from two experiments demonstrate the positive effects of these complexity measure-based features in trajectory classification. By improving the quality and accuracy of trajectory classification, the proposed approach in this research will benefit many applications of trajectory data analysis and mining, such as detecting abnormal moving vehicles in traffic video surveillance systems, understanding human movement patterns (e.g. tourism, commuting) from crowd contributed trajectory data via mobile devices .

Future research could focus on two additional aspects. First, the performance of classification related to different number of predefined classes and to large-scale data are important evaluating indicators for a multi-class classifier. Second, the current research only used four different movement types for trajectory classification. Other movement types, such as riding a motorcycle, should be included to assess the performance of this model.

Note

1. See http://physionet.org/physiotools/ApEn/