-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Geographic Information System
p-ISSN: 2163-1131 e-ISSN: 2163-114X
2014; 3(1): 45-61
doi:10.5923/j.ajgis.20140301.05
Estimate Instantaneous Solar Radiation Incident upon Terrain in Bushfire Zone Using Digital Elevation Model and Natural Disaster Forecast
Carl Y. H. Jiang
Centre for Intelligent Systems Research, Deakin University, Victoria, 3216, Australia
Correspondence to: Carl Y. H. Jiang, Centre for Intelligent Systems Research, Deakin University, Victoria, 3216, Australia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Effectively combined and practical methods have been applied into investigating the formation of bushfire in view of natural factors on the basis of a geographical location and local solar time under a clear weather. The instantaneous solar radiation accident onto the tilted surface of terrain in one bushfire burning zone is traced by its path. The extraterrestrial solar radiation is directly calculated by using approved astronomic formulas in which solar time and geometry are involved. Due to scattering and adsorption in atmospheric layer, extraterrestrial solar beam is classified into direct, diffuse and reflected beam when they are incident upon each tilted surface of terrain and received by it. Their calculations are performed by reliable empirical formulas respectively in a clear sky. The real values of geometric parameters of terrain are acquired by integrating digital elevation model with the corresponding satellite imagery. The solar time is determined by local time and geographical location of burning zone. Therefore, the solar radiation incident upon the complex terrain of burning zone is taking place instantaneously. The total radiant flux is sum of direct, diffuse and reflected radiant flux and located into an arbitrarily designed enclosure. It is treated to uniformly distribute and incident upon the tilted surfaces. The distribution of total radiant flux is still affected by complex terrain. Finally, by means of semi-infinite model and distribution of total radiant flux, the temperature at surface and inside soil is obtained respectively. The combined methods of research are useful in not only forecasting the risk of bushfire but also investigating soil drought.
Keywords: Solar radiation, Solar geometry, Bushfire, Soil Drought, Digital elevation model, Complex terrain, Satellite imagery
Cite this paper: Carl Y. H. Jiang, Estimate Instantaneous Solar Radiation Incident upon Terrain in Bushfire Zone Using Digital Elevation Model and Natural Disaster Forecast, American Journal of Geographic Information System, Vol. 3 No. 1, 2014, pp. 45-61. doi: 10.5923/j.ajgis.20140301.05.
Article Outline
1. Introduction
1.1. Overview
- Bushfire is closely related to weather, solar geometry and terrain. The solar geometrical factor seasonally and zonally determines the distribution of solar radiation, the factor of terrain spatially redistributes solar radiation arriving in the surface of the earth and weather temporally causes the difference of balance of solar radiation at the surface. The solar radiation is one of main factors influencing upon the vegetation on the surface the Earth. As to bushfire, the heat source is mainly from solar radiation before the vegetation is ignited[1]. Study on how solar radiation impacts on landscape is an important topic and procedure so as to obtain reliable and accurate data used in modelling bushfire spread in landscape, which cannot be ignored. However, researching solar radiation itself is a complex topic. When the extraterrestrial radiation travels through atmospheric layer, the intensity of solar radiation is decreased by an absorbing-scattering medium thus aerosol. The travelling direction of solar beam is altered by portioning it into direct beam and diffuse beam with different wavelength. The solar beam is also influenced by terrain when it arrives in the surface of the Earth. The concentration of traditional research in connecting solar beam and terrain has been located on the variation of intensity of solar beam with geometric parameter of terrain and local solar time. The less research topics have involved in the field of studying how solar radiant flux impacts upon vegetation at the surface and soil by means of knowledge of other disciplines. It can be discovered from the following literature review.
1.2. Literature Review
- Many researchers have been exploring in relationship between solar radiation and terrain. Some relevant aspects are shown as follows:1) Estimating surface solar radiation over complex terrain with DEMIn 2002, Hansen, L. B., N. Kamstrup, et al. [2]proposed a fast method for estimating the net short-wave radiation in high arctic mountainous areas is developed by combining Landsat-5 Thematic Mapper (TM) satellite data and a digital elevation model (DEM).In 2005, Kaicun, W., Z. Xiuji, et al.[3] used high-resolution satellite remotely sensed data to estimate surface net solar radiation over complex terrain combining with DEM. 2) Calculating extraterrestrial solar radiation on inclined surfacesIn 1986, Whiteman, C. D. and K. J. Allwine[4]provided a set of equations to calculate extraterrestrial solar radiation on a plane surface of arbitrary inclination and azimuth at any point on the Earth. The model inputs are the day of year, local standard time, longitude, latitude, and azimuth and inclination angles of the inclined plane. The outputs are instantaneous solar flux, and solar zenith and azimuth angles. Daily integrated solar flux on the plane surface can also be calculated, as well as the local standard time of sunrise and sunset.3) Estimating short and long-wave radiationIn 1998, Xue, Y., S. P. Lawrence, et al.[5] focused on long-wave radiation from sea and land surfaces and a technique was proposed for the derivation of land surface temperature (LST) and land surface emissivity retrieval using ATSR data in a new simultaneous split-window method. The net long-wave radiation was also considered in their research.In 2000,Xue, Y., D. T. Llewellyn-Jones, et al.[6], in the second paper, concentrated on short-wave radiation on sea and land surfaces by means of information from satellite. 4) Land surface reflectance, emissivity and temperatureIn 2002, Petitcolin, F. and E. Vermote[7]presented a method to retrieve surface reflectance, emissivity and temperature from spatial resolution data supplied by satellite. However, the main drawbacks for above researches are those:1. The topics were separately considered by researchers. They did not provide an instance to illustrate the correlation amongst solar geometry and geometric parameters of terrain instantaneously. The scales of some research were still remained at theoretic level. 2. Due to failure of gaining real values of terrain parameters (such as roughness and tilted surface area), an intrinsic and important parameter (such as radiant energy flow rate and distribution of temperature at surface) failed to be obtained. Those parameters play a vital role in not only calculating how much environmental temperature rises before vegetation is burnt but also determining soil temperature raised by absorbed solar energy. Therefore, the goals and features for this research are based on above factors and are shown in the following section.
1.3. Goals, Features and Scopes of Research
- In order to effectively illustrate correlation between solar geometry and geometric parameter of terrain, and then provide more useful information and data related to solar radiation for simultaneously modelling bushfire spread in landscape and smoke spatial dispersion, the following goals and features are to be carried out and achieved respectively in the process of the research:1. A bushfire zone is chosen from real geographic location.2. The solar time is a prominent feature in the pursuit of tracing the temporal and spatial motion of the Sun and the Earth. It is calculated and applied into modelling at all time.3. The extraterrestrial solar radiation is directly calculated by the existing approved astronomic formulas.4. The attenuation of solar beam is assessed by a set of empirical formulas so that direct solar radiation, diffuse and reflected radiation is easily to be handled respectively. 5. The geometric parameters are defined by the feature of topography. 6. The real values of geometric parameters of terrain are acquired by combining digital elevation model (DEM) and the corresponding satellite imagery. 7. The classified solar radiation incident onto the tilted surface of terrain is assessed by traditional formulas supplied by other researchers individually.8. All of classified radiant fluxes over complex terrain are enclosed. They are considered to be totally distributed over the tilted surfaces.9. The distribution of temperature at surface or inside soil is assessed by solar radiant energy incident upon the unit surface area per time within the enclosure. So-called enclosure is used to create two different thermodynamic systems and investigate energy transfer in detail. For sake of simplicity, energy leaving this enclosure is not to be considered. 10. Consider the bushfire always happens in a hot weather, all calculations are to be performed by assuming a clear sky.
1.4. Select Geographic Location
- The selected geographical location for investigating the solar radiation incident into a bushfire zone is (-36°70'10" S, 146°44'30" E; -36°83'60" S, 146°71'00" E) where there are several historic bushfires happened in Victoria, Australia (see Figure 1). Figure 1 is a satellite imagery captured by LANDSAT and the feature of terrain is illustrated by the corresponding DEM (SRTM3 offered by USGS) (see Figure 2). The burning zone is colored by red and marked by a circle sign (see Figure 1). It also appears in DEM (see Figure 2).
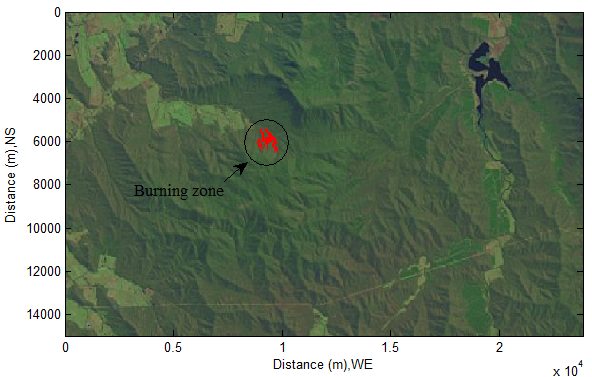 | Figure 1. Selected burning zone in satellite imagery |
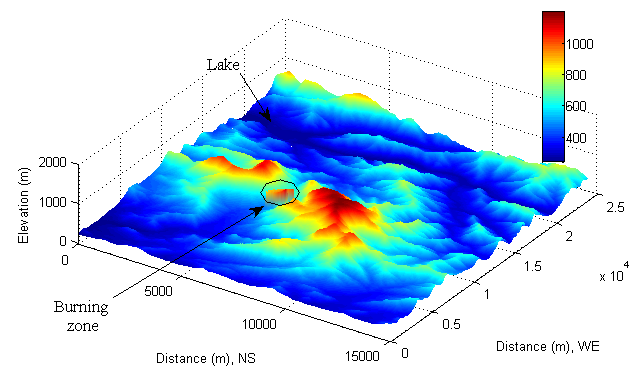 | Figure 2. Selected burning zone in DEM |
2. Fundamentals of Solar Geometry
2.1. Local Solar Time
- In solar application, the local solar time (LST) is much concerned, which is the time to be used in all solar geometry calculations. However, due to reflection of air, in practice, LST, in fact, is an apparent solar time for a place given longitude. LST usually differs from local time (LT), which is caused by the eccentricity of the Earth’s orbit and axial tilt.It can be actually shown as
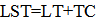 | (1) |
 | (2) |
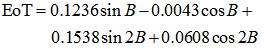 | (3) |
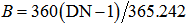 | (4) |
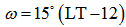 | (5) |
 at solar noon. ω is defined that in the morning
at solar noon. ω is defined that in the morning 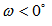 and in the afternoon
and in the afternoon 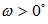 . The Earth rotates
. The Earth rotates 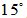 per hour. In this case, LT is located at K brand (Victoria, Australia).
per hour. In this case, LT is located at K brand (Victoria, Australia).2.2. Solar Geometry
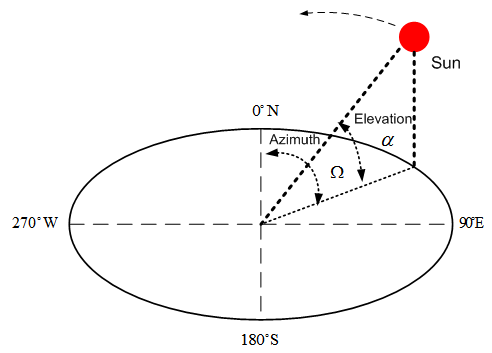
- Azimuth and Elevation AngleThe position of the Sun moves in sky is described by two angles: azimuth angle Ω and elevation angle α (see Figure 3).
 | Figure 3. Trajectory of the sun moving in space |
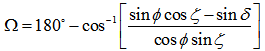 | (6) |
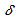 is solar declination angle.The range of azimuth Ω is
is solar declination angle.The range of azimuth Ω is 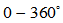 (see Figure 3). It is measured relative to the true north.When the Sun light arrives at the surface of the Earth, it generates zenith angle ζ, elevation angle α and solar declination angle δ due to the relative motion of the Sun and the Earth, Earth self-rotation (see Figure 4).
(see Figure 3). It is measured relative to the true north.When the Sun light arrives at the surface of the Earth, it generates zenith angle ζ, elevation angle α and solar declination angle δ due to the relative motion of the Sun and the Earth, Earth self-rotation (see Figure 4). 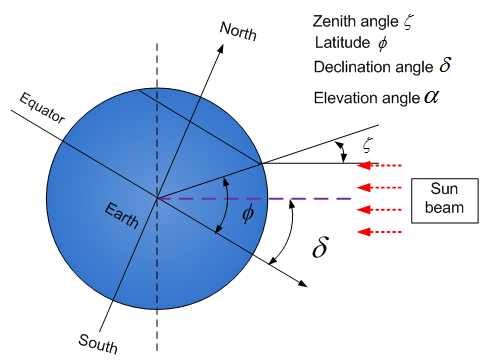 | Figure 4. Sun beam onto surface of Earth |
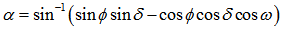 | (7) |
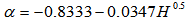 | (8) |
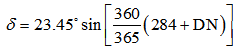 | (9) |
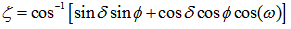 | (10) |
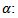
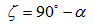 | (11) |
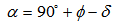 | (12) |
2.3. Classification and Attenuation of Solar Radiation
- Classification of Solar RadiationWhen extraterrestrial solar radiation reaches and goes through the Earth’s atmosphere, a part of the incident radiation is reflected into space; the solar radiation of another is partly lost due to absorption within atmospheric layer (see Figure 5). Its direction in sky is also altered by scattering. Therefore, the solar radiation is classified into two parts. One is a diffuse radiation; another is called direct-beam radiation which directly arrives at the surface of the earth from the Sun. The diffuse radiation is also classified into isotropic diffuse radiation and circumsolar diffuse radiation, which is following up the motion of the Sun. The circumsolar diffuse radiation can be resolved and the part of it is added into direct-beam radiation.
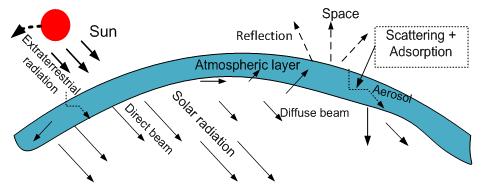 | Figure 5. Attenuation of solar radiation through atmosphere |
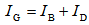 | (13) |
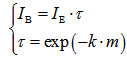 | (14) |
 is transmission coefficient.• k is known as extinction coefficient.• m is relative air mass.Instantaneous Extraterrestrial RadiationThe instantaneous extraterrestrial radiation on a horizontal surface is assessed by the following equation[8]:
is transmission coefficient.• k is known as extinction coefficient.• m is relative air mass.Instantaneous Extraterrestrial RadiationThe instantaneous extraterrestrial radiation on a horizontal surface is assessed by the following equation[8]: 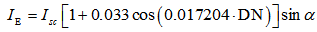 | (15) |
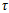 is expressed as the exponential form associated with extinction coefficient k and air mass m. The extinction coefficient k is composed of two parts: absorption coefficient and scattering coefficient. The extinction coefficient has the following physical properties when light passes through a scattering-absorbing medium:• It is a function of local temperature, pressure, composition of material and wavelength of the incident radiation. • It increases as the density of the absorbing or scattering species is increased.• It is the inverse of the mean penetration distance of radiation in a medium.• It is directly related to the optical thickness, which is defined as an integral of extinction coefficient within the thickness of local region. A large optical thickness means large attenuation of radiation. As seen above, the transmission coefficient τ is affected by not only the condition of weather but also the state of pollution in sky. In the case of bushfire, massive smoke is produced. The actual solar radiation arriving at the surface of terrain is dramatically attenuated by the scattering and adsorption happening in the smoke plume even if a clear-dry sky is assumed. However, in this paper, the discussion is confined to investigate the attenuation of solar radiation under the condition of clear-dry sky.Air MassThe air mass m depicts the path length of the solar beam through the atmosphere, which is simply defined as [11]
is expressed as the exponential form associated with extinction coefficient k and air mass m. The extinction coefficient k is composed of two parts: absorption coefficient and scattering coefficient. The extinction coefficient has the following physical properties when light passes through a scattering-absorbing medium:• It is a function of local temperature, pressure, composition of material and wavelength of the incident radiation. • It increases as the density of the absorbing or scattering species is increased.• It is the inverse of the mean penetration distance of radiation in a medium.• It is directly related to the optical thickness, which is defined as an integral of extinction coefficient within the thickness of local region. A large optical thickness means large attenuation of radiation. As seen above, the transmission coefficient τ is affected by not only the condition of weather but also the state of pollution in sky. In the case of bushfire, massive smoke is produced. The actual solar radiation arriving at the surface of terrain is dramatically attenuated by the scattering and adsorption happening in the smoke plume even if a clear-dry sky is assumed. However, in this paper, the discussion is confined to investigate the attenuation of solar radiation under the condition of clear-dry sky.Air MassThe air mass m depicts the path length of the solar beam through the atmosphere, which is simply defined as [11]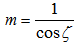 | (16) |
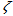 is assessed by equation(10). When the Sun is directly overhand, m is equal to one. Diffuse RadiationDiffuse ID can be estimated by the following equation[8]:
is assessed by equation(10). When the Sun is directly overhand, m is equal to one. Diffuse RadiationDiffuse ID can be estimated by the following equation[8]: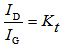 | (17) |
2.4. Empirically calculating Attenuation of Solar Radiation
- The air mass m mentioned above is usefully and conveniently used for calculating the intensity of the direct and diffuse component radiation of diurnal sunlight. Assuming that the diffuse component ID is 10% of the direct component IB, the intensity of global radiation IG and diffuse component can be estimated by the following correlated equations[12].
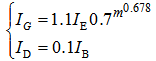 | (18) |
3. Solar Radiation Incident on Complex Terrain
- Due to scattering and adsorption (see Figure 5), the attenuated solar radiation becomes two parts: direct-beam radiation and diffuse beam radiation. When they arrive in complex terrain in the form of short wave, they are reflected by sloped hills in the form of long wave (see Figure 6). It completely differs from solar radiation incident on plain.
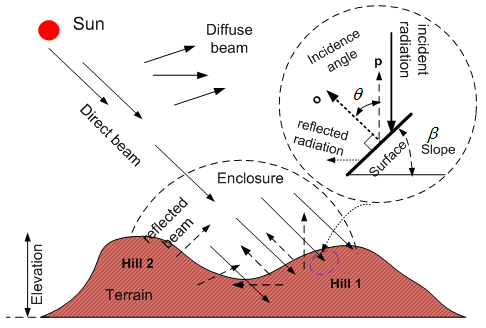 | Figure 6. Schematic of incident solar radiation on hills |
3.1. Direct Beam Incident on Slope
- The direct beam irradiation on a tilted surface from the cloudless sky is calculated as[11]:
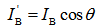 | (19) |
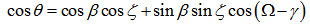 | (20) |
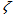 is zenith angle, Ω is azimuth angle of the Sun, γ is an aspect associated with the corresponding slope angle β at a given tilted surface (see Figure 3, Figure 4 and Figure 7).cosθ is able to alternately be expressed in the form of the dot vector[13] as (see Figure 6):
is zenith angle, Ω is azimuth angle of the Sun, γ is an aspect associated with the corresponding slope angle β at a given tilted surface (see Figure 3, Figure 4 and Figure 7).cosθ is able to alternately be expressed in the form of the dot vector[13] as (see Figure 6):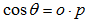 | (21) |
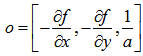 | (22) |
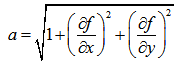 f is a continuous function of surface of terrain, x and y is a horizontal variable in a given three-dimensional coordinates (see Figure 7).
f is a continuous function of surface of terrain, x and y is a horizontal variable in a given three-dimensional coordinates (see Figure 7).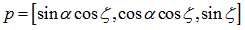 | (23) |
3.2. Diffuse Beam Incident on Slope
- Assuming isotropic sky, because only partial sky is visible, the diffuse beam incident on slope is then expressed as follows[11, 14]:
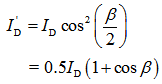 | (24) |
3.3. Reflection from Adjacent Slopes
- The partial radiation is reflected from adjacent slopes in the form of long wave. Assuming an uniform landscape, it is estimated as[11].
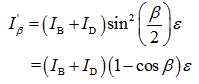 | (25) |
3.4. Total Incident Radiant Flux
- As mentioned of the preceding context, the total radiant flux received by the tilted surface mainly comprises three parts. It is shown by equation(26).
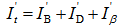 | (26) |
4. Geometric Parameters of DEM
4.1. Geometric Parameters
- The geometric parameters of DEM such as slope, aspect and roughness are extremely important as seen in the preceding context while investigating solar geometry. For a spatial curved surface (see Figure 7), given a continuous function f, its spatial height z can be mathematically described by the following equation:
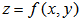 | (27) |
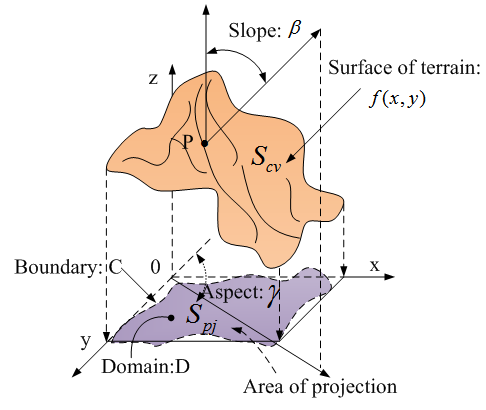 | Figure 7. Geometric parameters of surface |
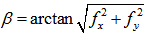 | (28) |
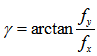 | (29) |
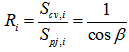 | (30) |
4.2. Local Moving Window
- Because continuous function f(x,y) usually is unknown, the analytical resolutions to equation (28)−(30) are difficult to be obtained.A 3×3 rectangle moving window has been proposed by researchers[15]. The principle is very simple. The treatment is performed by comparing the elevation of central cell c with the one of adjacent cells (see Figure 8).
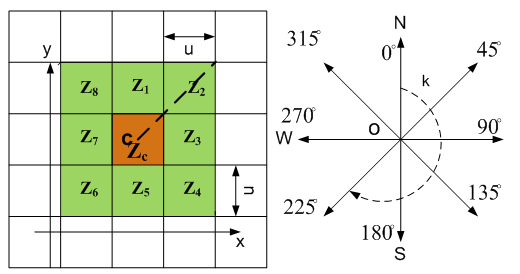 | Figure 8. 3×3 moving window |
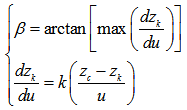 | (31) |
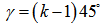 | (32) |
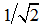 when k is odd and even respectively. As to the detailed explanation and application of geometric parameters used in DEM, it has been introduced by author[16, 17].
when k is odd and even respectively. As to the detailed explanation and application of geometric parameters used in DEM, it has been introduced by author[16, 17]. 4.3. Individual Geomorphologic Properties
- In this research, the main geomorphologic properties used for calculating instantaneous solar radiant flux incident onto the chosen burning zone in Figure 1 or Figure 2 are elevation, slope, aspect and burning area. In order to easily analyses the yielded results in the following sections, the properties of them are individually extracted by means of technique of linear indexing and presented in Figure 9 −Figure 12.According to the features of Figure 9 and Figure 10, it can be concluded that the selected burning zone is upslope. Except for several areas having smaller slope angles, most of them have larger slope angles, which ranges from 70−80° (steep hill) respectively. Furthermore, they are distributed unevenly in terms of their aspects (see Figure 11). Most of them remain at lower degree besides several extremes. In this case, it seems that at least, there are three valleys locating in the upslope hill. Approximately, the slope angles of them have 0°, 30° and 45° with the corresponding aspect angles: 50°, 290° and 300° respectively.The valleys certainly affect incident solar beam and distribution of solar flux in this zone. Such a fact is to be discovered in the following sections.Burning surface area is assessed by equation(30). As seen from Figure 12, the surface areas at upslope are larger than the ones at the bottom of hill). In short, the selected geographical location is a complex terrain. In above contexts, the local information is already gained. However, sometimes, the global information is also important in comparison with detailed results. In the following section, a manner of capturing global information is to be introduced.
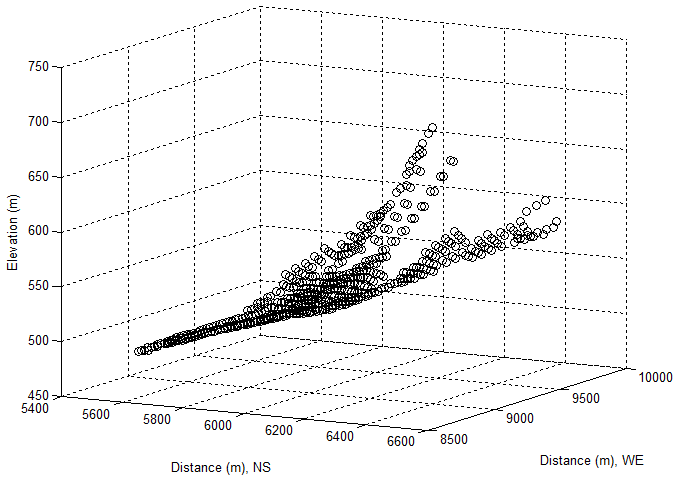 | Figure 9. Elevation of selected burning zone |
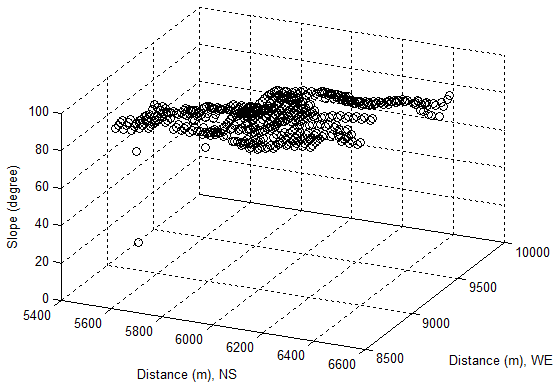 | Figure 10. Slope of selected burning zone |
 | Figure 11. Aspect of selected burning zone |
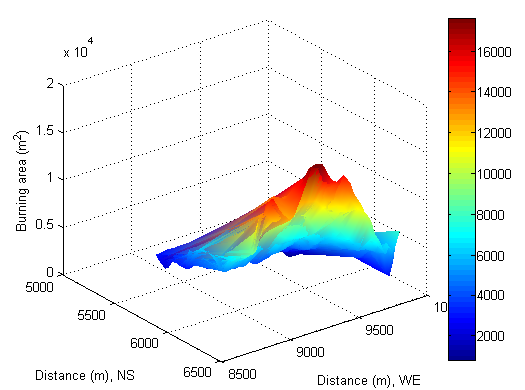 | Figure 12. Area of selected burning zone |
5. Shaded Relief
- The shaded relief is useful to globally understand how fast the Sun and Earth temporally and spatially motion while investigating solar radiation incident onto the complex terrain. The following shaded relieves of solar beam (see Figure 13−Figure 16) are formed by the variation of the cosine of incidence angle θ (see Figure 6) with respect to LST (local solar time) at the place where the bushfire burning zone locates (see Figure 1or Figure 2) due to motion of the Sun and the Earth. LST is calculated by equation (1). cosθ is calculated by equation(21). Sunrise and SunsetAaccording to the information offered by equation (8), it can be easily found that Sun beam appears slightly earlier at locations whose elevations are higher than the sea level in the morning (see Figure 13). In the afternoon, the Sun is still obviously discovered from those locations (see Figure 16).
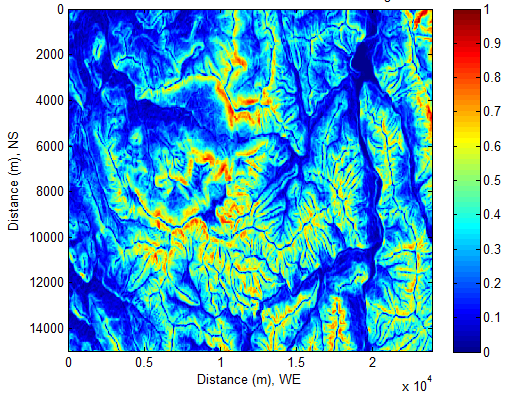 | Figure 13. At local time: 17-Oct-2013 08:34:45 |
 | Figure 14. At local time: 17-Oct-2013 10:43:13 |
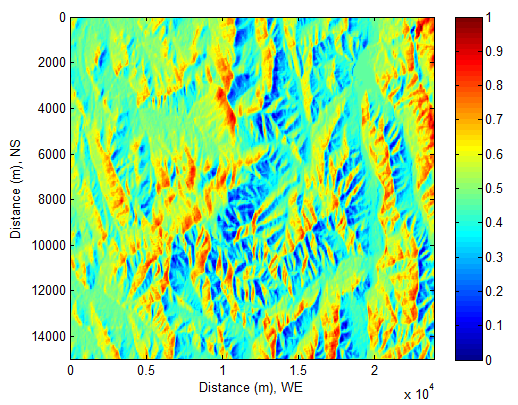 | Figure 15. At local time: 17-Oct-2013 13:15:08 |
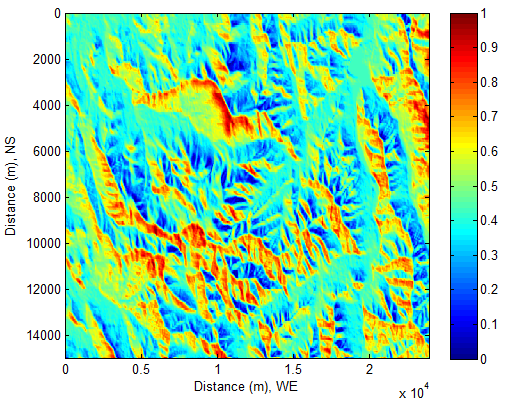 | Figure 16. At local time: 17-Oct-2013 16:44:36 |
6. Basics of Heat Transport
- In order to obtain accurate data of solar beam, in the preceding sections, much concentration is already located on the following topics:1. Solar Geometry: the temporal-spatial location of the Sun and the Earth;2. Attenuation of Solar Radiation: the process of solar beam travelling the atmospheric layer ;3. Geometric parameters of DEM: the mathematical expression of describing terrain and extracting real data from DEM;4. Shaded Relief: globally tracing variation of solar beam.However, the final target of research is to investigate how the solar radiant flux affects the observed objects (such as vegetation and pollutants) on or over the surface of the Earth. It is necessary to introduce some useful concepts used in heat transport so that the acquired information and data can be applied into further research.In classical physics, the solar beam has coexisting dual physical proprieties: wave (electromagnetic wave) and particle (photon). The radiant flux is an energy flow rate when it is absorbed by a unit surface within an enclosure (see Figure 6). In this research, the soil covered by vegetation is considered. To consider heat conduction implemented by solar radiation incident upon them (vegetation and soil), firstly, several assumptions are made as follows: 1. Solar energy transfer at the surface obeys the Fourier law. 2. Solar heat flux incident upon the surface remains constant within a limited time interval.3. The depth of soil covered by vegetation is infinite large. In fact, Earth radius is about 6.371kilometers. The solar energy vanishes at the superficial surface of the Earth.4. The physicochemical properties of components of soil are isotropic.Then, the distribution of temperature T for heat conduction in one-dimensional soil (see Figure 17) is shown as
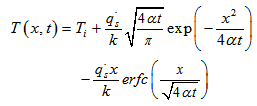 | (33) |
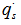 is the heat flux of solar radiation, the subscript s denotes surface. α is the thermal diffusivity of one substance. k is its thermal conductivity. x is the depth. erfc is the complementary error function having the properties: erfc(0)=1. t is time.The thermal diffusivity α is calculated by the following equation.
is the heat flux of solar radiation, the subscript s denotes surface. α is the thermal diffusivity of one substance. k is its thermal conductivity. x is the depth. erfc is the complementary error function having the properties: erfc(0)=1. t is time.The thermal diffusivity α is calculated by the following equation.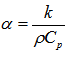 | (34) |
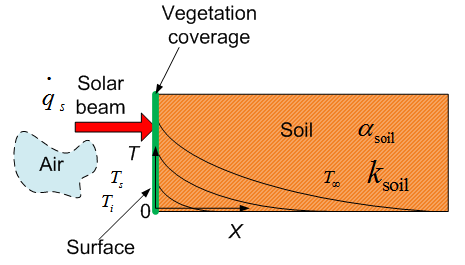 | Figure 17. Solar radiation incident upon the surface and distribution of its temperature in soil |
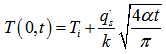 | (35) |
7. Results and Analysis
- In this section, the results about solar radiant flux are classified into two types to display and discuss. One is related to solar geometry. The definitions and limited applications associated with parameters of terrain are already introduced in the preceding sections. The results generated by the reported formulas are positioned into the subsection: Estimate Solar Radiant Flux from Sky. This approach provides an evidence of how to effectively integrate DEM with existing formulas and gain more information. They are separately discussed according to the classified solar flux source. Although solar radiant flux is classed into several types in terms of the type of solar beam travelling in sky, the solar energy entering an enclosure over the surface finally becomes “mixed” energy incident upon the titled surfaces within an enclosure (see Figure 6). Therefore, another is based on the mixed solar energy in an enclosure incident upon per unit surface area and unit time to calculate distribution of temperature over surface and inside soil. This part of results and discussions are located into subsection: Mixed Solar Radiant Flux Impacts on Vegetation and Soil.Strictly speaking, only energy (like mass) can exchange between two systems. However, in order to make use of existing formulas provided by researchers in different fields, the term of solar radiant flux is still remained when some explanations are made for some phenomena in the subsection: Estimate Solar Radiant Flux from Sky. Any variations only happen in the process of energy transfer. Such an approach does not bother investigating distribution of temperature in the subsection: Mixed Solar Radiant Flux Impacts on Vegetation and Soil. This matter may easily be confused in practice, especially in interdisciplinary research. Estimate Solar Radiant Flux from Sky
7.1. Direct Radiant Flux Incident on Slopes
- The direct beam irradiation on a tilted surface is calculated by equation (19).According to equation (14) and (20), under the condition of clear sky, at least, five parameters (such as slope, aspect, zenith angle, solar azimuth and hour angle) directly and simultaneously affect the direct beam incident on the tilted surface.Intuitively, the intensity of direct radiant flux incident onto the tilted surface seems to be that it increases with the Sun ascent until solar noon. Then it starts to decrease with time.Such an intuitive sense of understanding direct solar beam incident onto the tilted surface is not fully true.The observation can be carried out by selecting a same location with respect to the solar time. If select an area which locates at distance: 5600−6500 meter in North-South (latitude) and 8800−9400 meter in West-East (longitude) as an observed area (see Figure 18), it is easily to find out a fact that the maximum radiant flux of direct beam approximately reached to 900 W∙m-2. However, in two hours later, thus at local time: 17-Oct-2013 10:43:13 (see Figure 19), the maximum radiant flux approximately dropped to 800 W∙m-2; at local time: 17-Oct-2013 13:15:08 (see Figure 20), the maximum radiant flux rose to 850 W∙m-2. In eight hours later, at local time: 17-Oct-2013 16:44:36 (see Figure 21), the situation changed dramatically. The maximum radiant flux approximately dropped to 380 W∙m-2 in the original observed area. Of interest is that a new phenomenon of shift was generated due to Earth self-rotation. On the one hand, the direct radiant flux appeared in a new area at distance: 5600−6500 meter in North-South (latitude) and forward extended distance: 8500−8800 meter in West-East (longitude), the minimum direct radiant flux approximately was 200 W∙m-2(see Figure 21). On the other hand, it also appeared in another new area at distance: 5600−6500 meter in North-South (latitude) and 9500−9700 meter in West-East (longitude). The maximum direct radiant flux approximately rose from 400 W∙m-2 (see Figure 18) to 550 W∙m-2(see Figure 21); the minimum direct radiant flux dropped from 100 W∙m-2 to 50 W∙m-2. As seen from above observations, the direct radiant flux incident onto the tilted surface of terrain is directly influenced by the following main factors: solar geometry, solar time and geomorphologic parameters of terrain a, hour angle represented by the variation of longitude relative to the direct solar beam with respect to solar time due to the rotation of the Earth. If other factors are not considered into, on the basis of above fact, the additional energy added into bushfire from solar radiation varies with local longitude and solar time.
7.2. Diffuse Radiant Flux Incident on Slopes
- The diffuse radiation flux ID is calculated by combining equation (18) and (24). Because it is about 10% IB, as expected, the intensity of diffuse radiant flux is smaller than the one of direct beam (see Figure 22−Figure 25). The feature of its distribution looks similar in different solar time, but it differs from the one of direct radiation incident onto the tilted surfaces. However, comparing the distance in West-East (longitude) shown in Figure 22 with the one in Figure 24 and Figure 25, the phenomenon of shift appeared in the distribution of diffuse radiant flux too.However, if the local time is chosen as a reference point, it can be found that diffuse radiant flux requires less time to reach to the same shift. That is because diffuse beam travels in opposite direction to Earth rotation.
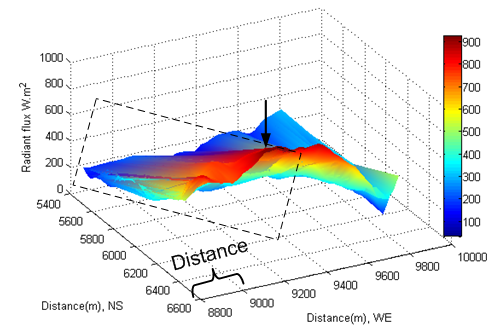 | Figure 18. Direct beam at local time: 17-Oct-2013 08:34:45 |
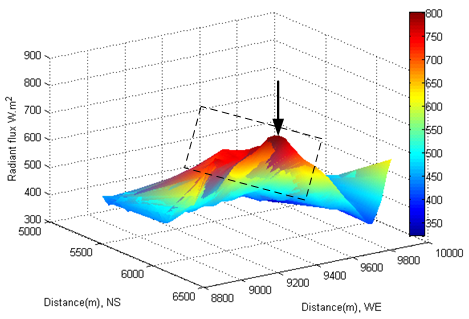 | Figure 19. Direct beam at local time: 17-Oct-2013 10:43:13d |
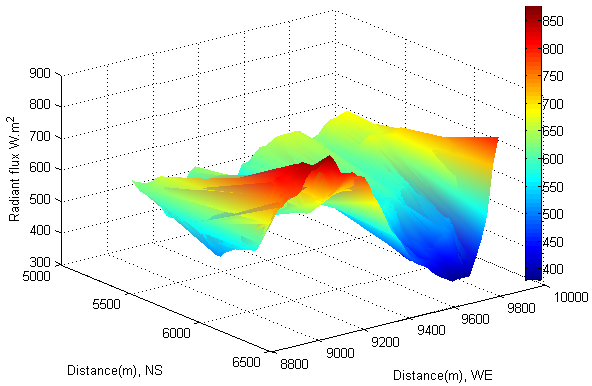 | Figure 20. Direct beam at local time: 17-Oct-2013 13:15:08 |
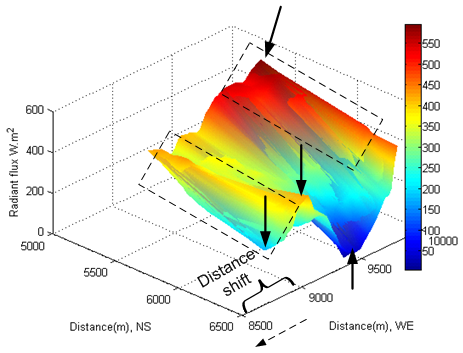 | Figure 21. Direct beam at local time: 17-Oct-2013 16:44:36 |
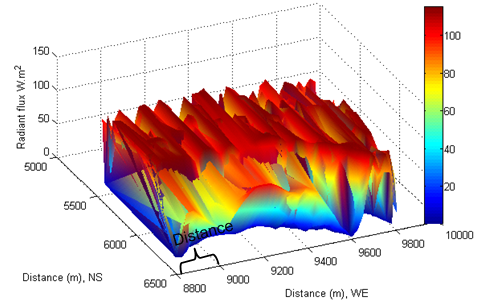 | Figure 22. Diffuse beam at local time: 17-Oct-2013 08:34:45 |
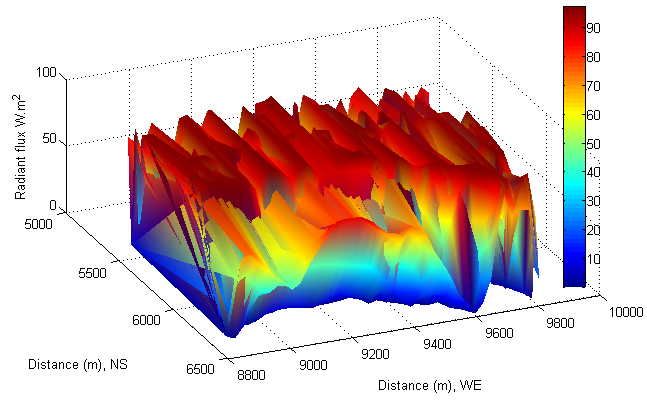 | Figure 23. Diffuse beam at local time: 17-Oct-2013 10:43:13 |
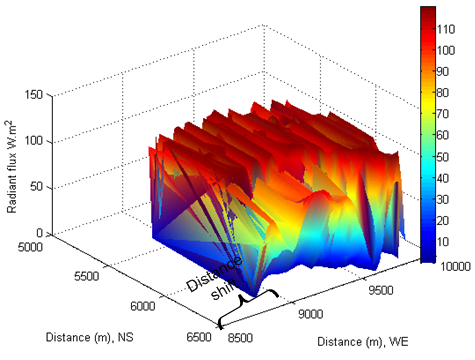 | Figure 24. Diffuse beam at local time: 17-Oct-2013 13:15:08 |
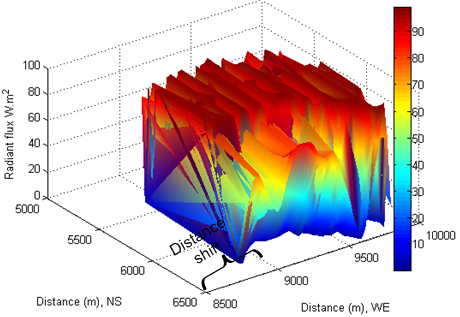 | Figure 25. Diffuse beam at local time: 17-Oct-2013 16:44:36 |
7.3. Reflected Radiant Flux from Adjacent Slopes
- The reflected radiant flux is calculated by equation (25). Because the surface is covered by vegetation, the albedo ε =0.25 is chosen in the calculation[19]. In general, the intensity of reflected radiant flux lies between diffuse radiation flux and direct radiation flux. In other words, the reflected radiant flux from adjacent slopes still remains the high temperature of air over tilted surfaces even if the Sun approaches to sunset (see Figure 29). Similarly, the phenomenon of shift is also discovered in the distribution of reflected radiant flux by comparing the distance in West-East (longitude) (see Figure 26) with the one in Figure 29. The phenomenon of shift is directly caused the Earth’s self-rotation and direction of solar beam travelling in sky. The diffuse radiant flux is shifting from one place to another in opposite direction to the rotation of the Earth. However, the shift of direct and reflected radiant flux is directly caused by Earth rotation. This discovery is very useful and reasonable to treat total radiant flux as a “flowing energy” flux over the tilted surfaces within the arbitrarily designed enclosure.
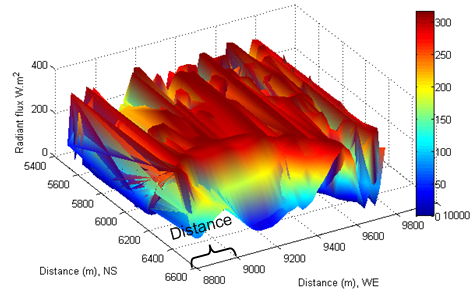 | Figure 26. Reflected radiation at local time: 17-Oct-2013 08:34:45 |
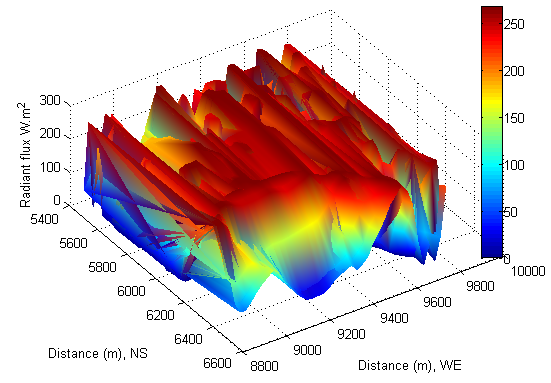 | Figure 27. Reflected radiation at local time: 17-Oct-2013 10:43:13 |
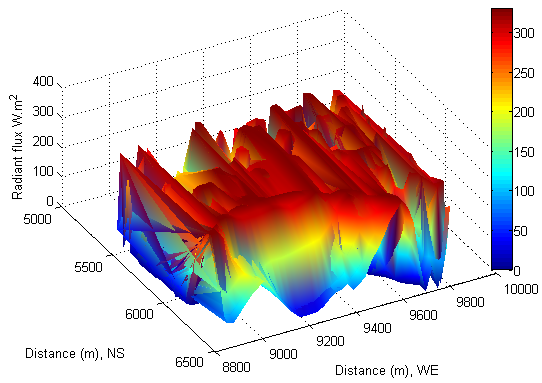 | Figure 28. Reflected radiation at local time: 17-Oct-2013 13:15:08 |
 | Figure 29. Reflected radiation at local time: 17-Oct-2013 16:44:36 |
7.4. Total Radiant Flux Incident on Slopes
- The total radiant flux (see Figure 30−Figure 33) received by the tilted surface is assessed by equation(26). In this case, the radiant flux of direct, diffuse and reflected beam is uniformly mixed and incident on the each tilted surface. The magnitude of total radiant flux is larger than the individual one mentioned above. The typical difference is that the “shape” of total radiant flux is different from the one of diffused and reflected beam respectively; however, it is analogous to the one of direct beam. In other words, it is still influenced by its terrain and solar time.An obvious difference between the direct radiant flux and the total radiant flux is that the direct radiant flux is much influenced by the rotation of the Earth and the total radiant flux is less influenced by it. That is because the total radiant flux is already treated as a “flowing energy” over per unit tilted surface and unit time within the enclosure (see Figure 6). The total radiant flux entering the enclosure is mainly influenced by terrain with respect to solar time. Accordingly, non phenomenon of shift is discovered from Figure 30−Figure 33. This approach simplifies the complex case much. Based on the results of radiant flux in Figure 30−Figure 33. There are two approaches can be further performed.
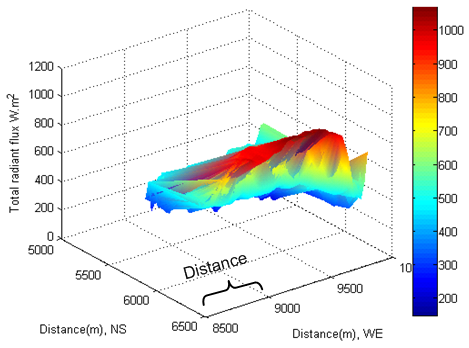 | Figure 30. Total radiant flux at local time: 17-Oct-2013 08:34:45 |
 | Figure 31. Total radiant flux at local time: 17-Oct-2013 10:43:13 |
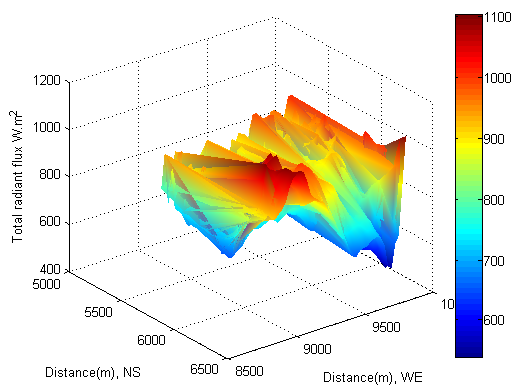 | Figure 32. Total radiant flux at local time: 17-Oct-2013 13:15:08 |
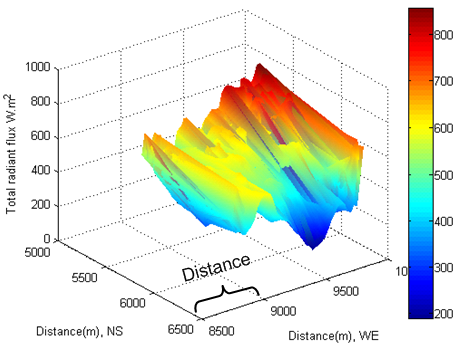 | Figure 33. Total radiant flux at local time: 17-Oct-2013 16:44:36 |
7.5. Distribution of Temperature at Surface of Terrain
- The concerned topic in this research is how the temperature is distributed at the surface of terrain because igniting vegetation on the surface and bushfire spread has a close relation to it. To investigate distribution of temperature, it has to roll back the topic of total solar radiant flux.As seen from Figure 30−Figure 33, the radiant flux varies with the different locations affected by geometric parameters of terrain with respect to time. However, for the sake of easily calculating, it can still be considered as a constant at each spot within an interval time.To perform the calculation of temperature, the equation(35) is chosen. Each solar radiant flux shown in Figure 30 at different location is regarded as a constant within three hours. The thermal properties of soil are listed in Table 1. The sampling is performed at two time points. Two different initial temperatures 298.15 K and 308.15 K are assigned to calculation respectively to distinguish different local time.
|
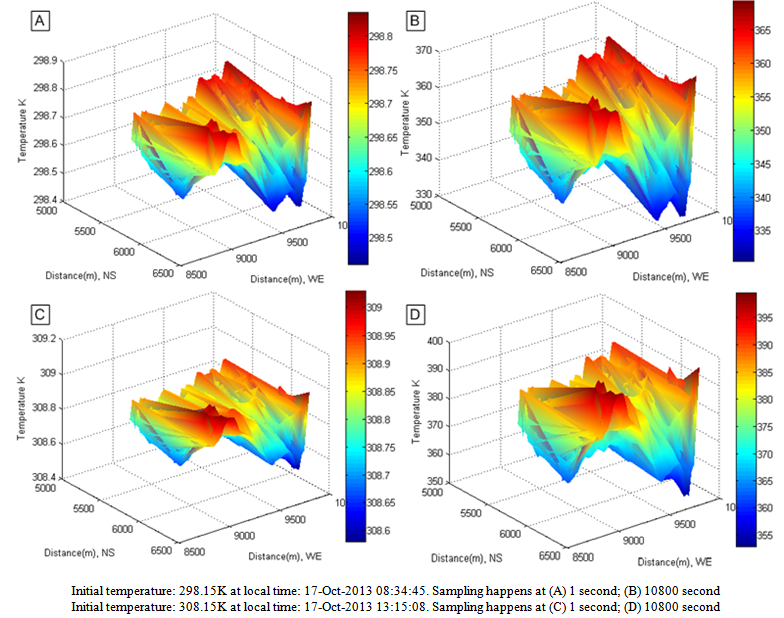 | Figure 34. Temperature profile on the surface is assessed by total radiant flux with |
7.6. Distribution of Temperature inside Soil
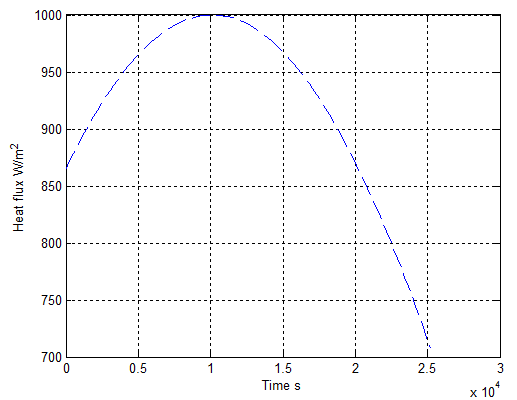
- In the previous section, the temperature impacting upon the vegetation is already investigated. However, the higher temperature is able to not only vaporize water component inside vegetation but also drain the soil. In order to investigate this process, assume that a profile of solar radiant flux varying with time (within 7 hours), on average, is shown as the one in Figure 35. Then, applying the relevent data in Table 1 into equation(33) combining with the initial temperatures at different surfaces and time in Figure 36 yields the profile of temperature in soil represented by both Figure 37 and Figure 38.It can be found that the solar radiant energy is capable of draining the soil quickly within seven hours daily under clear weather. The dryness of soil may be reduced after sunset. It may be recovered to the original state due to rain or other natural factors.However, under extreme condition, if the soil is continuously dried for a long time, it results in larger area of dead vegetation and easily igniting dried vegetation at surface.Consequently, this approach is also useful in forecasting drought.
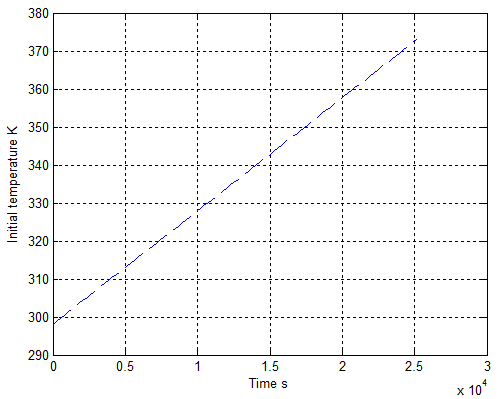 | Figure 36. Initial temperature at surface |
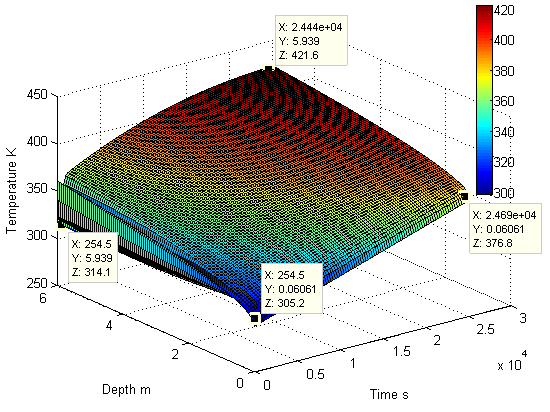 | Figure 37. Depth of penetration of temperature |
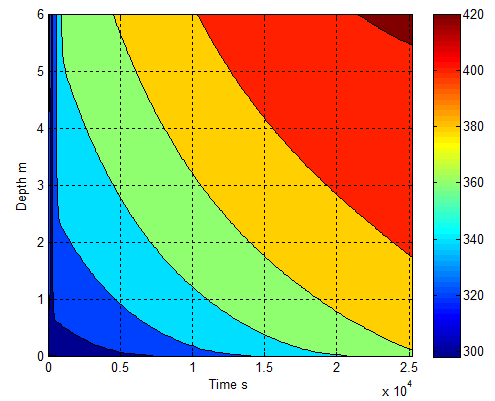 | Figure 38. Distribution of temperature in soil |
8. Conclusions
- Achievement of current workOn the basis of the results of instantaneous radiant flux incident on tilted surfaces in a selected burning zone, it can be discovered that 1. Although the attenuated solar beam can be classified into three parts: direct beam, diffuse beam and reflected beam they reaches to the tilted surface after the instantaneous extraterrestrial radiation passing through atmosphere due to scattering and absorption, the thermal properties of them appears a lot of differences when they are incident onto the tilted surfaces. The direct radiant flux incident onto the tilted surface of terrain is directly influenced by two main part factors: solar geometry, solar time and geomorphologic parameters of terrain, hour angle. It is sensitive to the rotation of the Earth related to the variation of local longitude. The direct radiant flux is a largest proportion of global solar radiation impacting onto the tilted surface at ground. The intensity of reflected radiation from adjacent slopes is larger than the one of diffuse radiation. This part of radiant flux indirectly indicates that the temperature of air over tilted surface does not decrease immediately when sunset starts. A phenomenon of shift can be discovered by distribution of direct, diffuse and reflected radiant flux respectively. They have individual feature incident onto the tilted surface. 2. The feature of distribution of total radiant flux is similar to the one of direct radiant flux except for different intensity when it distributes over tilted surfaces. The main difference between them is that the total radiant flux is less affected by the rotation of the Earth. So non phenomenon of shift is found. That is because the total radiant flux is located into an enclosure and treated as a “flowing energy” incident upon per unit titled surface area and unit time. The distribution of temperature relies on the one of total radiant flux, consequently it distributes unevenly as well.3. At the surface of Earth, the temperature is a main parameter to indicate how fast the water component in vegetation is evaporated and the soil is drained. In the research, it has been found that total solar flux is able to cause vegetation and soil lose an amount of water if remain it constantly within a time interval, especially at noon time. 4. The fact is that bushfire always happens at one spot under a dry and hot weather. The combined method applied in this research has brought into effect in effectively indicating the distribution of temperature, forecasting the risk of bushfire and investigating soil drought.
Future Work
- The solar radiant energy is one important energy source in igniting vegetation and accelerating bushfire spread. The results of current work are to be further considered into aspects of investigating the energy transported and distributed in smoke dispersion, evaporating water component of vegetation and bushfire spread at ground.
ACKNOWLEDGEMENTS
- Author wants to offer special thanks to Professor Jing. X. Zhao at Shanghai Jiao Tong University for supplying desired data used in this research.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML