-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Geographic Information System
p-ISSN: 2163-1131 e-ISSN: 2163-114X
2013; 2(3): 47-65
doi:10.5923/j.ajgis.20130203.03
Digital Elevation Model and Satellite Imagery Based Bushfire Simulation
Carl Y. H. Jiang
Centre for Intelligent Systems Research, Deakin University, Victoria, 3216, Australia
Correspondence to: Carl Y. H. Jiang, Centre for Intelligent Systems Research, Deakin University, Victoria, 3216, Australia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Modelling bushfire spread is full of challenge owing to its complexity. A novel and accurate manner of integrating satellite imagery with digital elevation model to model large scale bushfire has been proposed. In this modelling, the burning zone and smouldering zone were already classified in the digital image in terms of the difference of gray level of each colour component and the separated time interval was generated. The technique of indexing the same observed objects between two and three dimensional systems was illustrated in detail. By means of such a technique, the classified data from satellite imagery successfully integrated with the corresponding digital elevation model. A simple model for determining the direction of bushfire spread with a constant average velocity in landscapes was then proposed. A modelling bushfire spread as an application was performed in digital elevation model. Reversely displaying selected information which gained and implemented in digital elevation model has been achieved in the original remote sensing imagery to verify the results of modelling. Several desired features of modelling bushfires shown in results accurately appeared.
Keywords: Bushfires Modeling, Digital Elevation Model, Digital Image Processing, Linear Indexing
Cite this paper: Carl Y. H. Jiang, Digital Elevation Model and Satellite Imagery Based Bushfire Simulation, American Journal of Geographic Information System, Vol. 2 No. 3, 2013, pp. 47-65. doi: 10.5923/j.ajgis.20130203.03.
Article Outline
1. Introduction
- The digital elevation model (DEM) plays an important role in geographic information system (GIS). The applications of DEM integrating with additional information can range many fields such as hydrological studies[1-4], soil investigation and modelling[1-5] and natural disaster studies for flooding[6-9]. However, any reports related to modelling bushfires in landscape using DEM have not been found. The main difficulties in this field are those:• No necessary information about observed objects in landscapes can be acquired from DEM, • Lack in necessarily understanding how bushfire spreads in landscapes.The efforts without using DEM can be found from some previous works. Several researchers[10-13] proposed a series of abstract mathematic models and performed some small scale experiments as a main point of studying.However, the achievement made by those researches could not represent large scale bushfires[14].Consequently, a new idea in studying the large scale bushfire is to be proposed in this paper. The novel approach is an interdisciplinary study. It combines and utilizes the unique features of DEM and the corresponding satellite imagery and then applies some knowledge from other disciplines such as meteorology, combustion and transport phenomena to resolve the following drawbacks and main difficulties:DEM fails to supply the information of distribution of vegetation besides elevation,Satellite imagery only offers two-dimensions (2-D) based information,How bushfire spreads in landscapes (affected by geometric shape of terrain),How the pollutant ( thus smoke) spatially disperses, How smoke impact upon the surface,How to estimate the amount of released energy and mass during bushfire spread,How the bushfire spread is affected by solar radiation (spread velocity is different at day and night time),And so onObjectives and scales of researchNevertheless, the scale in this paper is only to focus on 1. How the distribution of vegetation is classified in the remote sensing imagery. 2. How the classified data from the remote sensing imagery is transferred into DEM.3. How to determine the direction of bushfire spread combining the remote sensing and DEM.4. How to create a linear index in a matrix.5. How to convert a vector point in a coordinates of DEM and generate linear indices.6. How to model a simple case of bushfire spread in landscape based on DEM for further approaches. 7. How to display the information gained from modeling in DEM into original remote sensing imagery reversely.Meanwhile, some basic concepts and techniques used in the digital image processing and the geomorphology integrating with the features of DEM are to be included.
2. Methodology
2.1. On Identifying Substances in Remote Sensing Imagery
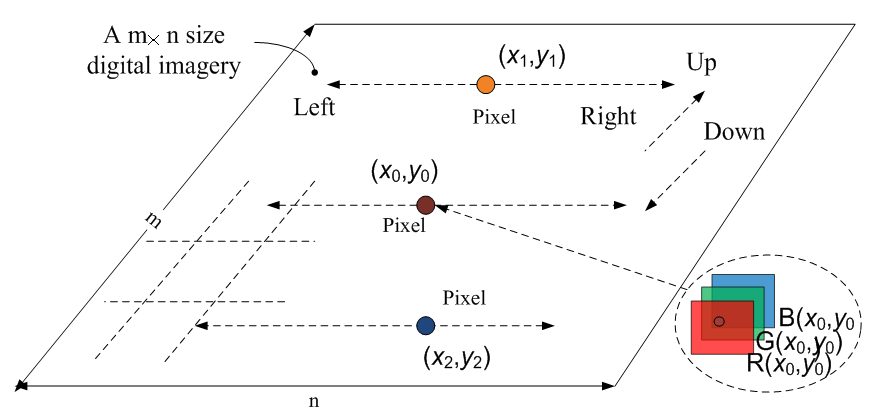
- Because this research is based on remote sensing imagery and digital elevation model (DEM). Some concepts related to digital image processing are briefly mentioned as follows. They may be helpful in understanding the procedure that how the data are captured by sensors and stored in the form of digital imagery, why identifying objects must be classified and how to perform it by means of creating new techniques.Principle of Remote Sensing Remote sensing is a method of acquiring information about an object or phenomenon without physically contacting. It consists of a series of process before information is obtained (see Figure 1 ). The electromagnetic wave, energy and spectrum play an important role in transferring signal, imaging, analysing object and phenomenon. The platform usually is a satellite or aircraft. Sensors consist of several devices having different functionalities. The digital imaging happens in a charge-coupled device (CCD) to catch each incoming photon and digitally expose it in a matrix-like linear CCD array, and then a digital image is formed[15].
 | Figure 1. principle of remote sensing |
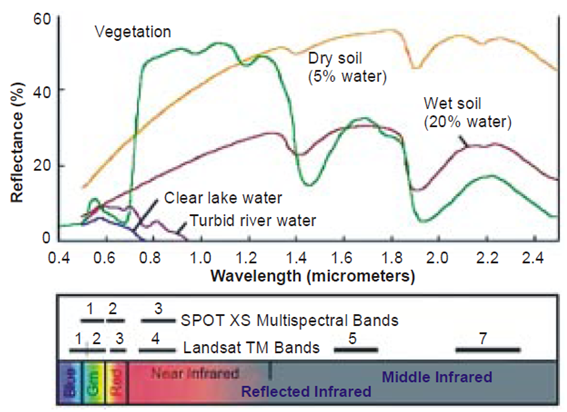 | Figure 2. typical spectral reflectance curves for vegetation, soil and water[16] |
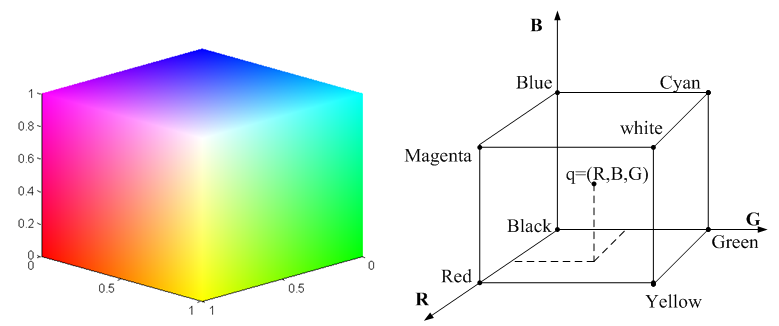 | Figure 3. RGB tube and RGB space |
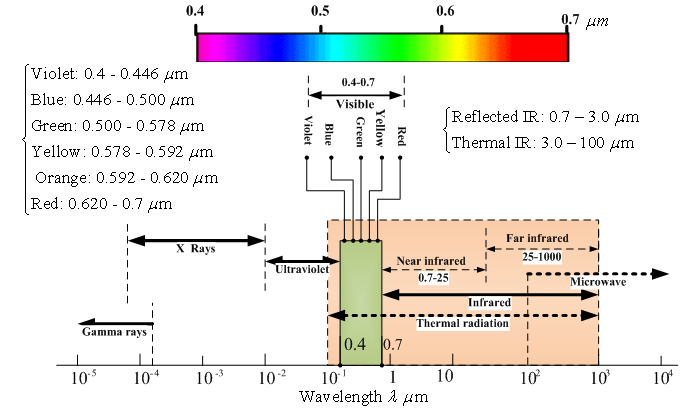 | Figure 4. the spectrum of electromagnetic radiation (redraw it based on[17-18]) |
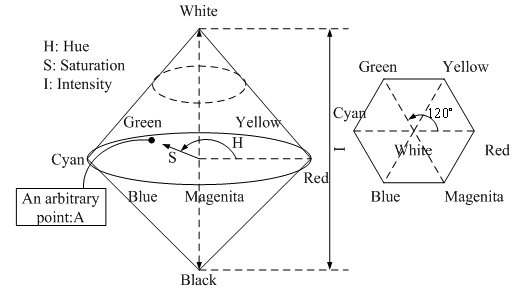 | Figure 5. relationships between RGB space and HIS space |
 | Figure 6. HIS space-based remote sensing imagery Identify Substances |
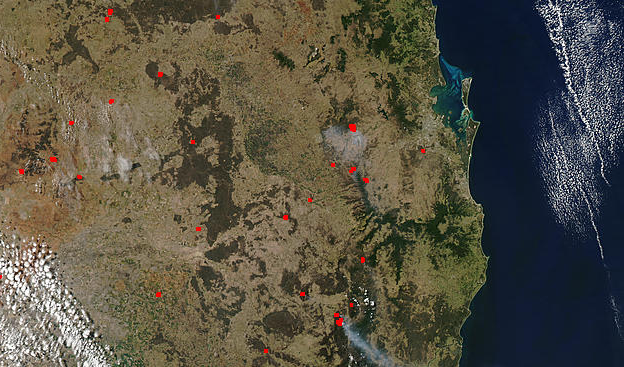 | Figure 7. Aqua MODIS image was acquired on September 22, 2003[20] |
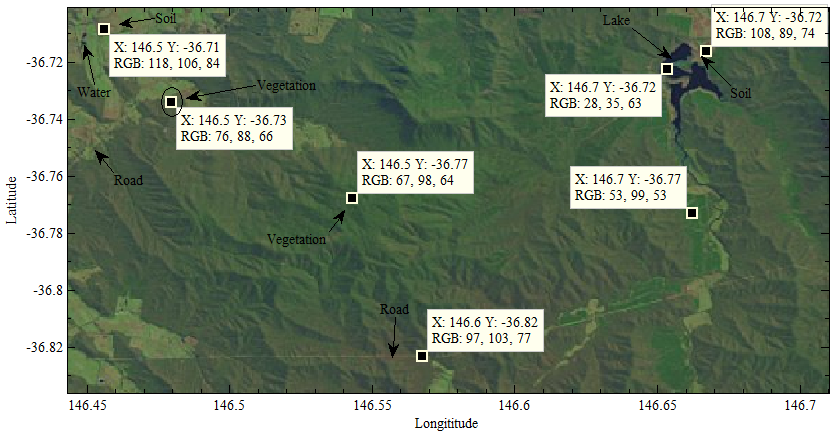 | Figure 8. selected landscape of remote sensing imagery for modeling |
2.2. On Further Development of Remote Sensing Imagery Integrating with Digital Elevation Model
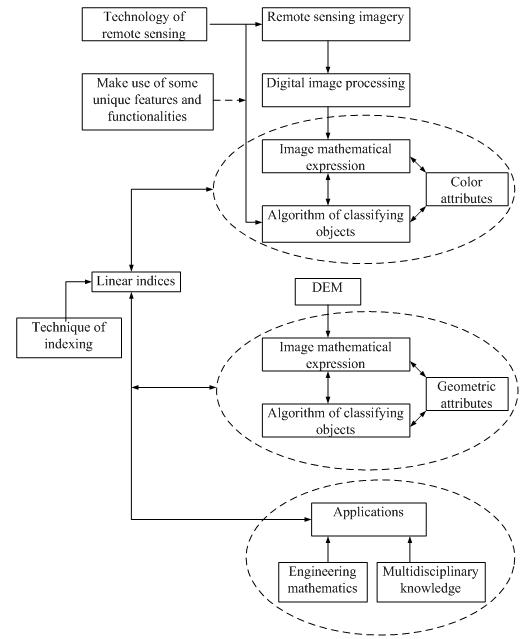 | Figure 9. schedule graph of further development integrating remote sensing imagery with DEM |
2.3. Concept of Processing Digital Image
- A Digital Image as a Matrix and Basic PropertiesAs mentioned before, the matrix of a digital image was formed when each photon moved in CCD. Thus each incoming photon is attracted by the positive voltage of the electrode at different time interval. The digital image processing relies on such a built-in attribute. However, it does not mean all information can be found from this built-in attribute. It should be integrated with other attributes in handling specific cases.A. Mathematic expression of a digital imageAll pixels in a system of coordinates thus a given digital image with a particular size can be mathematically expressed by using a matrix (which is similar to the mathematical structure of DEM, which is to be discussed later) as follows.
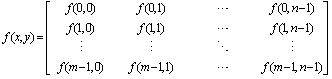 | (1) |
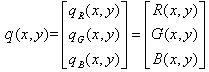 | (2) |
 | Figure 10. resolved color components of a size m×n×3 RGB image |
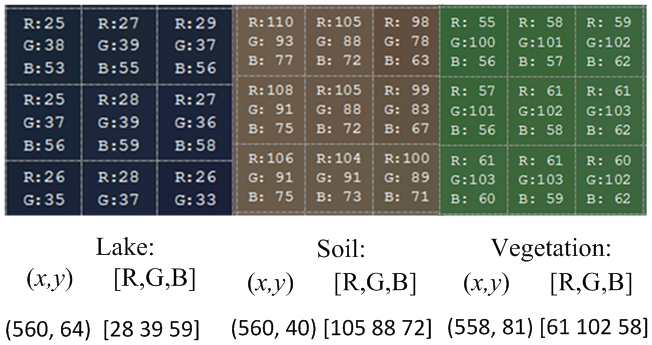 | Figure 11. Color sampling of observed objects in the remote sensing imagery |
 | Figure 12. schematic of algorithm for burning tendency test |
2.4. Burning Tendency Test
- A. Algorithm of burning tendency The algorithm of burning tendency test is developed from sampling diversely (see Figure 8 and Figure 11) in terms of spectral signature of substance (see Figure 2).The general mathematical expression can be depicted by equation(3).
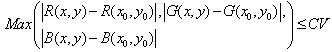 | (3) |
|
 | Figure 13. algorithm of burning tendency test |
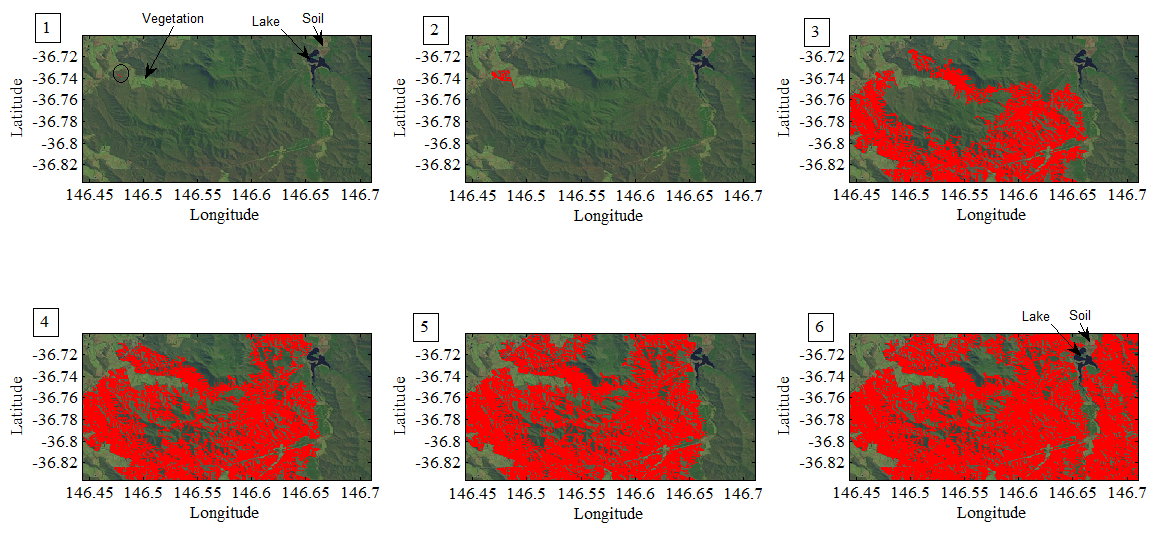 | Figure 14. burning tendency test in the remote sensing imagery |
2.5. Classifying Burning and Smouldering Zone in a Remote sensing Imagery
- In bushfire tendency test, the extra area (thus the difference between new area and original area at one time interval) represents that the area of bushfire spread is enlarged from its original state with respect to elapsed time. If bushfire does not spread in the extra area yet, it can be named as smouldering zone.The problem is that how to distinguish the smouldering zone (pixels) from previous zone (pixels). Directly distinguishing them using the existing linear indices is impossible. The technique that can be utilized is technology of digital image processing by means of the Image Tool™ in MATLAB®. However, processing a digital image associates with many concepts and techniques, it is impossible to detail them in this paper. A typical example of classifying burning and smouldering zone is illustrated as follows. A. Some necessary steps in classifying burning and smouldering zoneThere are three states of bushfire spread in Figure 15((1), (2) and (3)). They are generated by burning tendency test. The linear indices and pixels in the third state cover previous two states. Similarly, the second state covers first state.
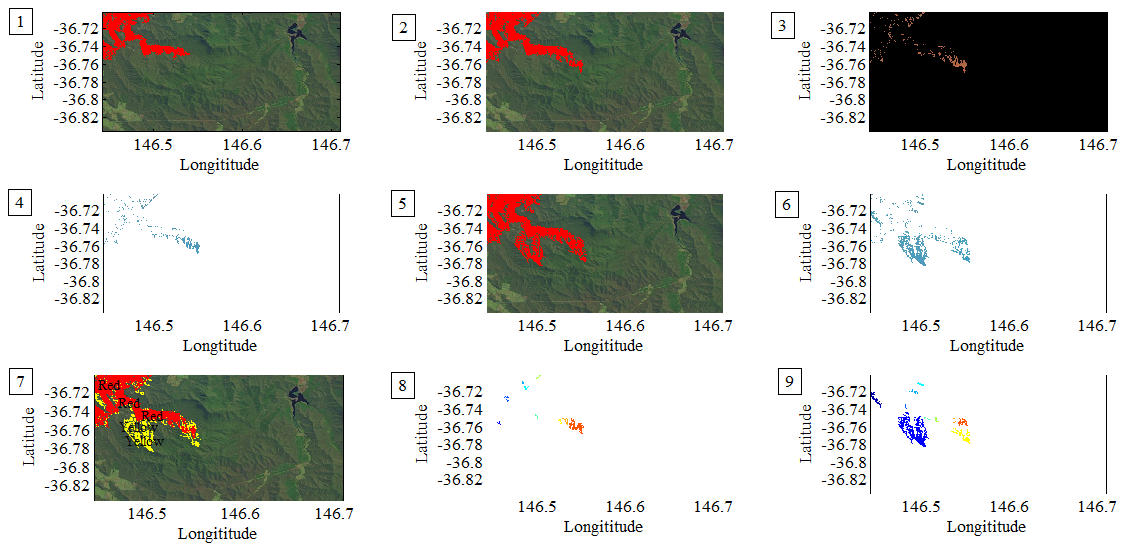 | Figure 15. illustrate the procedure of classifying burning and smouldering zone in the remote sensing imagery |
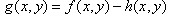 | (4) |
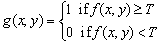 A built-in function: graythresh provided by MATLAB® uses Otsuian method, which is based on the normalized histogram. In this case, it is capable of gaining a global threshold using the values extracted from the blue or red band resolved from the original image. The function graythresh generates a normalized intensity value that lies in the range[0, 1].Step6: conversion into a binary imageUp to this point, the compliment of image in (6), similar to the image in (3) is able to be converted into a binary image using the built-in function: im2bw.Step7: find connected components of pixels in the binary imageOnce the conversion of the compliment of image in (6) into a binary image is achieved, the connection of pixels for the third state can be dealt with using built-in function: bwconncomp. Then the generated value is inserted into other built-in function: regionprops. Those built-in functions provide several useful properties of image such as NumObjects and PixelIdxList. They supply information of number of connected objects and their corresponding linear indices. Eventually all indices for two smouldering zones thus the images in (4) and (6) can be picked up and confirmed.Step8: show burning and smouldering zone using different colours in one imageInserting linear indices of (2) and (6) into the same image assigning different colours such as red (burning zone) and yellow (smouldering zone) produces a new image in (7).B. Display reduced burning and smouldering zone separatelyHowever, from practical view, displaying all burning and smouldering zone separately requires a lot of memory in computer. The best way is to display selected area (e.g. the actual number of pixels in the region is larger than 80) like cases in (8) and (9), the colours ware added by built-in function: label2rgb for distinguishing objects in the same classified region. If compare cases in (8) and (9) with images in (4) and (6) respectively, the scales of objects in (8) and (9) are reduced. Such a treatment does not affect the quality of modelling because bushfire spread itself is a stochastic process. The small area is also burnt and covered. The objects in (8) and (9) are to be transferred into the corresponding DEM by using their discovered linear indices later.As to detailed usage of built-in functions mentioned in this paper, refer to user’s manual of MATLAB®.
A built-in function: graythresh provided by MATLAB® uses Otsuian method, which is based on the normalized histogram. In this case, it is capable of gaining a global threshold using the values extracted from the blue or red band resolved from the original image. The function graythresh generates a normalized intensity value that lies in the range[0, 1].Step6: conversion into a binary imageUp to this point, the compliment of image in (6), similar to the image in (3) is able to be converted into a binary image using the built-in function: im2bw.Step7: find connected components of pixels in the binary imageOnce the conversion of the compliment of image in (6) into a binary image is achieved, the connection of pixels for the third state can be dealt with using built-in function: bwconncomp. Then the generated value is inserted into other built-in function: regionprops. Those built-in functions provide several useful properties of image such as NumObjects and PixelIdxList. They supply information of number of connected objects and their corresponding linear indices. Eventually all indices for two smouldering zones thus the images in (4) and (6) can be picked up and confirmed.Step8: show burning and smouldering zone using different colours in one imageInserting linear indices of (2) and (6) into the same image assigning different colours such as red (burning zone) and yellow (smouldering zone) produces a new image in (7).B. Display reduced burning and smouldering zone separatelyHowever, from practical view, displaying all burning and smouldering zone separately requires a lot of memory in computer. The best way is to display selected area (e.g. the actual number of pixels in the region is larger than 80) like cases in (8) and (9), the colours ware added by built-in function: label2rgb for distinguishing objects in the same classified region. If compare cases in (8) and (9) with images in (4) and (6) respectively, the scales of objects in (8) and (9) are reduced. Such a treatment does not affect the quality of modelling because bushfire spread itself is a stochastic process. The small area is also burnt and covered. The objects in (8) and (9) are to be transferred into the corresponding DEM by using their discovered linear indices later.As to detailed usage of built-in functions mentioned in this paper, refer to user’s manual of MATLAB®.2.6. Concept of DEM and Basic Properties
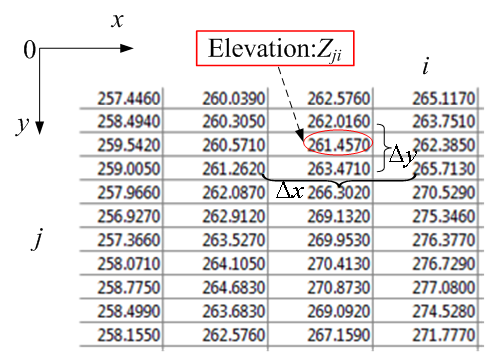 | Figure 16. data of DEM: elevation and corresponding grid interval |
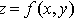 | (5) |
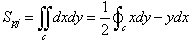 | (6) |
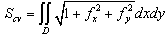 | (7) |
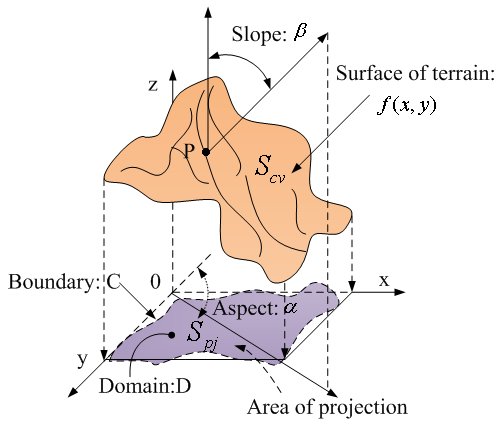 | Figure 17. mathematical expression of terrain |
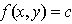 , and c is an arbitrary constant, z is elevation. And then at the point P (see Figure 17), along its normal, it yields its gradient shown as
, and c is an arbitrary constant, z is elevation. And then at the point P (see Figure 17), along its normal, it yields its gradient shown as 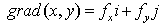 | (8) |
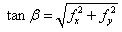 | (9) |
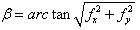 | (10) |
 (see Figure 17) is expressed as
(see Figure 17) is expressed as  | (11) |
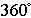 . In other manner, the aspect is also thought of as the direction of the biggest slope vector on the tangent plane projected onto the horizontal plane.Defining the unit roughness Rk is based on the relation between the surface of terrain and DEM, which is defined as the ratio of the surface area Scv to its projection onto the horizontal plane Spj for the kth unit of surface area (see Figure 17).
. In other manner, the aspect is also thought of as the direction of the biggest slope vector on the tangent plane projected onto the horizontal plane.Defining the unit roughness Rk is based on the relation between the surface of terrain and DEM, which is defined as the ratio of the surface area Scv to its projection onto the horizontal plane Spj for the kth unit of surface area (see Figure 17).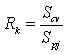 | (12) |
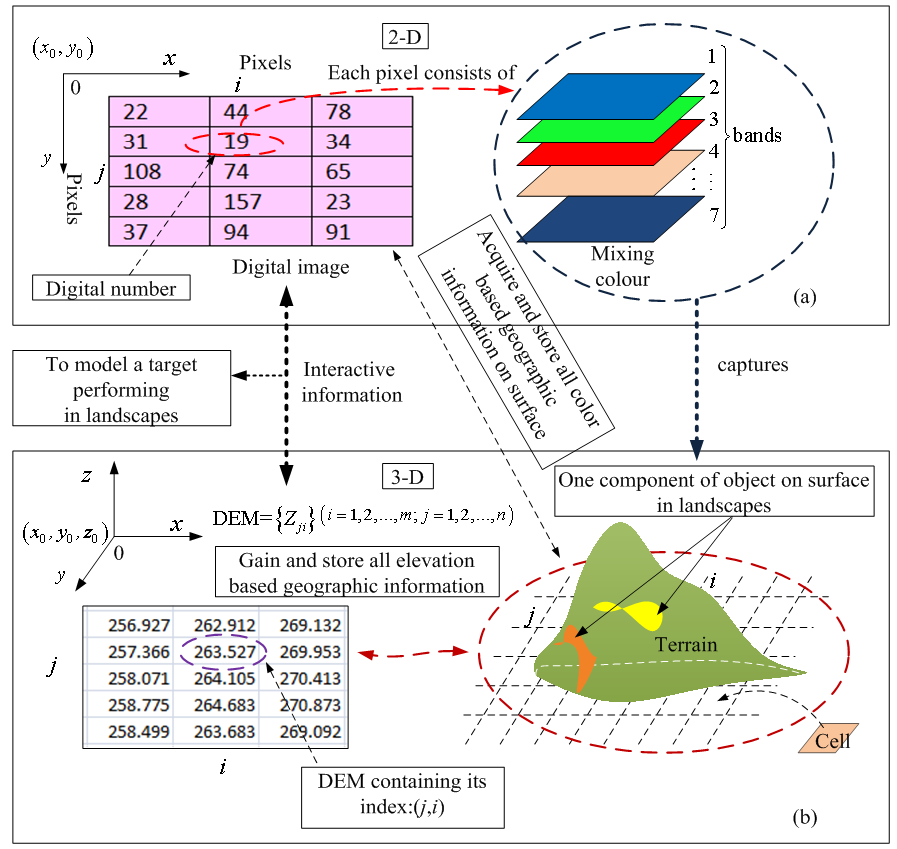 | Figure 18. schematically illustrates the correlation between remote sensing imagery and corresponding DEM |
2.7. Correlation between Digital Image and DEM
- In the last sections, several vital concepts used in following fields were already introduced separately.1) Digital image processing.2) The principle of classifying vegetation in the remote sensing image to generate burning and smouldering zone.3) Mathematically describing the surface of terrain.4) Linking geomorphology to DEM.At this stage, of importance is discuss how to connect two different coordinates system and accurately transfer collected data and information into other system and model specific case. Selecting the same location for both DEM and remote sensing imagery is the most important pre-condition for accurately establishing relationship between two and three-dimensional coordinates in those the same observed objects are located and transferring the interactive data.The main unique features and functionalities associated correlation are summarized and illustrated in Figure 18.Figure 18 shows that each paired index (j,i) in the satellite imagery (see Figure 18(a)) not only contains the digital number of each colour component stored in one pixel of the 2-D digital imagery but also links the corresponding elevation shown in the 3-D DEM (see Figure 18(b)). On the other hand, in the coordinates of DEM, a series of elevation Z thus{Zji},j=1,2,…,m, i=1,2,…,n, where m and n are integers, consists of DEM with m × n same size cells(thus, equivalent to pixels) . The subscript j and i are the same indices as the ones in the satellite imagery and denote the sequence of row and column respectively in a matrix, however, the paired index (j,i) can be merged into a linear index (see equation (13) ) in practice. In other words, the digital imagery has the same 2-D coordinates system as the one shown in DEM (refer to the coordinates: x-y and x-y-z in Figure 18). Mathematically speaking, for a satellite imagery and DEM having the same geographic location, a same size matrix exists in both of horizontal plains to describe the different physical properties (thus the digital number of colour and the elevation respectively) in the third dimension z. However, the digital number of colour is hidden in 2-D only.
2.8. Create Linear Indexing Using MATLAB®
- The technique of indexing is playing a vital role in developing GIS[22-26]. It is very useful to accurately link the same observed objects in different systems so as to effectively integrate and individually analyse the different physical properties appeared in the different systems. This process facilitates information and data exchange mutually.MALTB® is a matrix-based powerful package. If there is a matrix A with m×n size and subscripts are (j,i), the linear index is produced as follows.
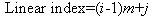 | (13) |
2.9. Conversion of Vector Point in the Coordinates of DEM
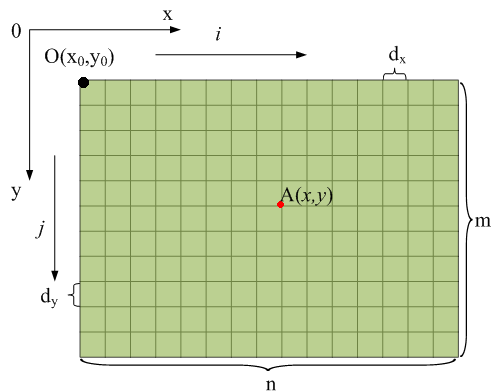 | Figure 19. Vector point conversion in the coordinates of DEM |
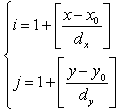 | (14) |
2.10. A Simple Model for Determining Direction and Shape of Burning Spread
- Determining the direction of the burning front is a hot spot in the bushfire investigation[27], some researchers used electric fans to generate wind in their laboratories and then determine the direction of burning front[28]. Determining Direction of Bushfire Spread in Terms of the Center of MassHowever, in modelling large scale bushfire in landscapes, the direction of burning front can be estimated by either meteorological measurement or connecting the corresponding mass centre located in the burning zone and the smouldering zone respectively. The latter was selected in this modelling. As to how to classify in the remote sensing imagery, refer to section 2.5.The geographic location for the centre of mass of burning zone and smouldering can be decided by using a tool box: Image Tool™ in MATLAB® as well (see point G and C in Figure 20). The angle of bushfire spread can then be estimated by Equation(15).
 | (15) |
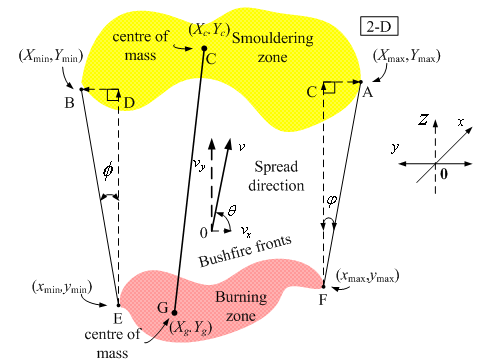 | Figure 20. Determine direction of burning front |
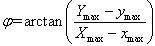 | (16) |
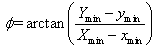 | (17) |
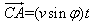 | (18) |
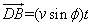 | (19) |
2.11. Digital Elevation Model and Satellite Imagery Chosen for Bushfire Simulation
- In practice, DEM is always located in a given physical coordinates. The unit often used to calculate is meter (see Figure 21) rather than geographic degree. Furthermore, the velocity is a vector. In order to position the movement of observed objects in landscapes, indicating the geographic orientation is necessary. The symbols NS and WE shown in Figure 21 are defined to denote the orientation of north-south and west-east respectively in a local Cartesian coordinates according to latitude and longitude indicated in Figure 8.In this paper, the DEM chosen for bushfire simulation has the same geographic location (−36°70'10'' S, 146°44'30'' E; −36°83'60'' S, 146°71'00'' E) as the one of the satellite imagery (see Figure 8) captured by the satellite Landsat. In this area (Victoria, Australia), several large scale bushfires used to take place.
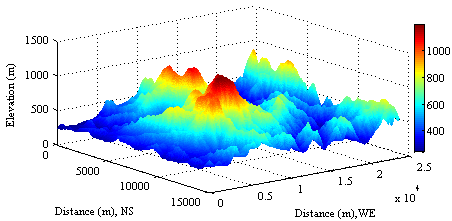 | Figure 21. DEM is defined in meter |
3. Results
3.1. Display Burning and Smouldering Zone in Digital Elevation Model
- The geographic locations of burning (see Figure 22) and smouldering (see Figure 23) zones are transferred from those shown in (8) and (9) of Figure 15 respectively. This procedure is one important step for visualizing results and further approaches by means of data transfer.
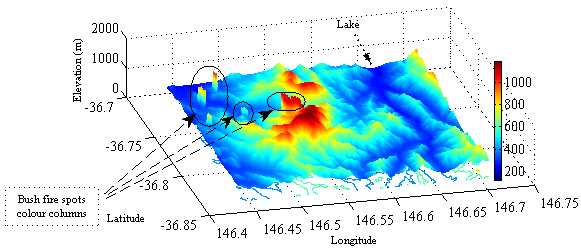 | Figure 22. Burning spots are located in burning zones |
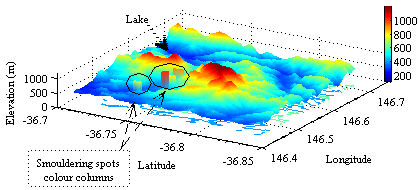 | Figure 23. Smouldering spots are located in smouldering zones |
3.2. Bushfire Spread in Digital Elevation Model
- According to the proposed model (see section 2.10), the bushfire spread is assumed downwind and the constant average velocity is equal to
 . The result of modelling demonstrates this process in landscapes (see Figure 24). The detail is illustrated in Figure 25. In this application, the conversion between positions of bushfire spread and the local coordinates is required (see section 2.9) except for using the technique of linear indexing to transfer information from remote sensing imagery (see (7), (8) and (9) in Figure 15; Figure 22 and Figure 23).
. The result of modelling demonstrates this process in landscapes (see Figure 24). The detail is illustrated in Figure 25. In this application, the conversion between positions of bushfire spread and the local coordinates is required (see section 2.9) except for using the technique of linear indexing to transfer information from remote sensing imagery (see (7), (8) and (9) in Figure 15; Figure 22 and Figure 23).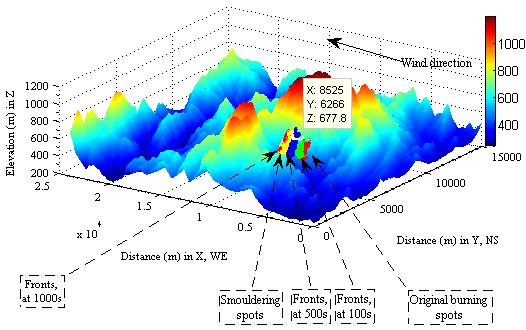 | Figure 24. Bushfire spreads from original spots to smouldering spots with average velocity ( ) ) |
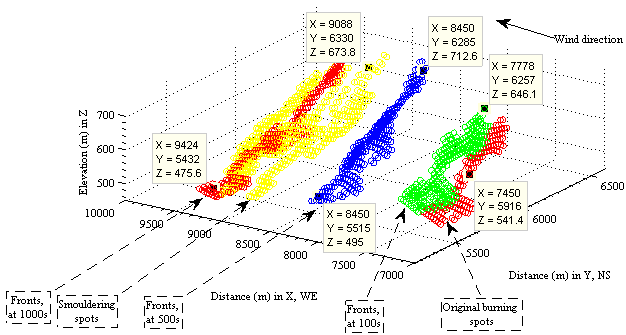 | Figure 25. Detailed bushfire spread with the constant average velocity |
3.3. Display Information from DEM in Digital Imagery
- In the last example, modeling bushfire spread in DEM was performed on basis of transferred data from remote sensing imagery and the technique of indexing and vector point conversion. Similarly, the result produced by modeling in DEM is also able to be displayed in the corresponding remote sensing imagery to verify the result.
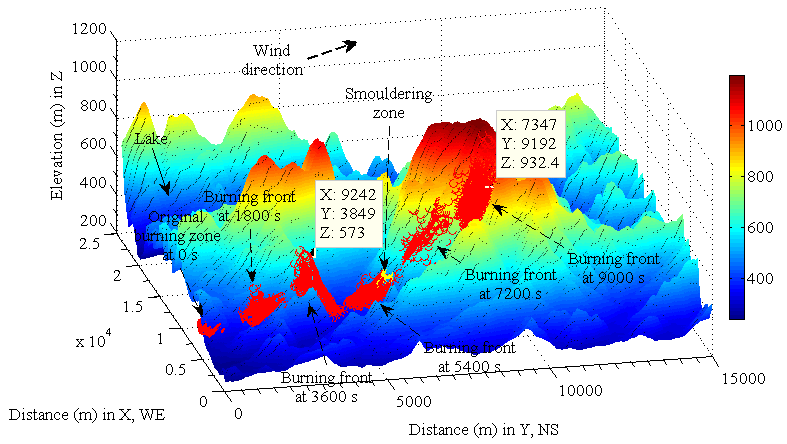 | Figure 26. modeling bushfire spread in DEM based on the geographical information and collected data transferred from digital imagery |
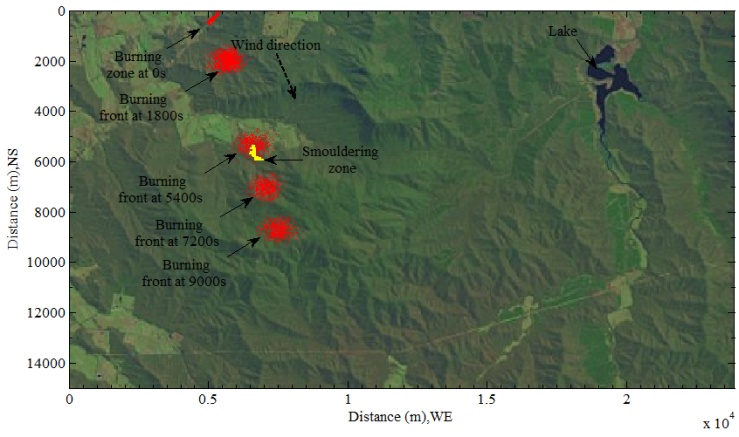 | Figure 27. Display selected information of modeling from DEM in the original digital imagery |
4. Discussion
- As seen from (8) and (9) of Figure 15 and Figure 22−Figure 23, the data chain can be established within two different dimensional systems if the corresponding scale in two different coordinates is consistent. Through the data chain, the desired information is transferred from 2-D imagery into 3-D DEM. Of importance for modelling bushfire spread in landscapes is to know distribution vegetation. The process has been achieved by indexing the same observed objects during data transfer. It is obviously discovered that bushfire spread varies with slopes of terrain under the constant average velocity and the width is increased with the forward movement of bushfire front (see Figure 25).On the other hand, most results generated in DEM can be reversely displayed in the remote sensing imagery (see Figure 26 and Figure 27 ). Above two example have proved how much important the linear indices are. Although they are generated in different manner, they have same integers due to the same size matrix they are used. They can be selectively transferred into other system to model some behaviour and display results. Furthermore, the some attributes of substances and objects can be altered relying on liner indexing.
5. Conclusions and Future Work
- A. Summarize the current work Several important and basic concepts and techniques used in modelling bushfire spread have been briefly reviewed and creatively proposed. The following targets in this paper have been achieved:1. The useful information about the distribution of vegetation was extracted from the two-dimensional based remote sensing imagery to ensure bushfire occurs within bushes. The principle was also introduced descriptively. This is a pre-condition for modelling bushfire in the large scale landscapes.2. The technique of indexing used to indicate the same observed object within two -coordinates system was explained in detail. This technique is very useful in temporal and spatial modelling.3. The classified data were successfully transferred into the three-dimensional based DEM and displayed by means of the technique of indexing. It plays a vital role in transferring and visualizing data.4. A technique of converting a vector point in a coordinates into a corresponding matrix was discussed. This is one of vital techniques for modelling bushfire spread in landscape using DEM.5. A simple model used for determining direction of bushfire spread in terms of the measured centre of mass for both burning and smouldering zone was proposed. This is an ideal model only used for testing how to apply the transferred data into modelling bushfire spread in landscapes.6. A demonstrated modelling bushfire spread in DEM was carried out. This practice is a foundation to further improve the proposed model of bushfire spread.7. The selected information which gained and implemented in DEM has been displayed in the original remote sensing imagery to verify the results of modelling. As seen, linear indices play an important role in indexing objects in different physical systems, modelling in another system (DEM) and reversely displaying results of modelling into the original system where desired data are collected and transferred from.B. Future workHowever, as mentioned at the beginning of this paper, more significant issues have been brought forth during this research and to be considered and carried out in the future study:1. In order to apply transferred data into application, a simple case of bushfire spread in landscapes using DEM has been studied. This simple case indeed implies much potential, significant and various meaning. For DEM itself, a lot of geographic features hidden in it such as surface area, slope of terrain can be explored and applied. The slope is one of most important geographic parameters. It can be considered for calculating the surface area of burning on the basis of the plain area from the given satellite imagery.2. To simplify the case supplied in the paper, the average velocity of bushfire spread was assumed as a constant. However, in reality, bushfire spread at surface is influenced by not only the distribution of vegetation in landscapes but also the features of terrain and meteorological factors. Therefore, the idea for estimating the real velocity of bushfire spread may be yielded from the one of local wind. A modified coefficient will be introduced into the real velocity of wind and then establish a comprehensive correlation between two different velocities may become quite necessary. The real velocity of wind may be estimated by using the geostrophic wind.3. Naturally, bushfire spread and smoke spatial dispersion can be simultaneously modelled based on the technique of indexing and vector point conversion.4. The corresponding mass and energy released from the burning bushes can be estimated on the basis of other physical models. The energy in this approach will be a real quantitative calculation by means of some valuable parameters from DEM, the theory of transport phenomena. Those approaches will be different from the concept of energy accounted for the principle of remote sensing in this paper.
ACKNOWLEDGMENTS
- Author wants to offer special thanks to Professor Jing. X. Zhao at Shanghai Jiao Tong University for supplying desired data used in this research.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML