Shuxin Huang
Loss of Job, Independent Research Person, Shanghai, 200240, China
Correspondence to: Shuxin Huang, Loss of Job, Independent Research Person, Shanghai, 200240, China.
| Email: |  |
Copyright © 2025 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The data on student performance in learning the Navier–Stokes (NS) equation, in 2023, accompanied by published data, indicate that semi-semester study is not beneficial for undergraduate students in mastering the equation. Semi-semester studies in 2021 and 2023 showed lower scores in NS equation examinations than those from one-semester studies in 2020 and 2022. The errors caused by not grasping both the NS equation and the boundary condition showed the same defect in the semi-semester study for students who lost more than 5 points (out of a possible 20) on the examination. Moreover, the error ratio caused by forgetting the equation alone for all the students was approximately 20% for semi-semester study and approximately 0% for one-semester study, showing the difference between the students and the time effect of the study.
Keywords:
NS equation, Exam, Undergraduate student, Inverse of the Stokes second problem, Hypothesis test, Semi-semester study
Cite this paper: Shuxin Huang, Semi-Semester Effect on Learning the Navier-Stokes Equation, American Journal of Fluid Dynamics, Vol. 14 No. 1, 2025, pp. 1-4. doi: 10.5923/j.ajfd.20251401.01.
1. Introduction
The curriculum of engineering fluid mechanics has been taught without a change in the syllabus by the author of this paper since 2007. However, the COVID-19 epidemic in China from 2020 to 2022 changed the teaching circumstances and curriculum. The original syllabus contained a midterm, which was canceled in 2020 and 2022 because of the epidemic [1,2]. The examination of the Navier-Stokes (NS) equation is usually conducted in the midterm but was transferred to the final examinations for those two years. The special circumstances in 2020 and 2022 also formed a check on the study-time effect, and one-semester study seemed superior to semi-semester study for the NS equation [2].The NS equation is a basic equation used to describe the flow of fluids, such as air and water, and is expressed by the following three equations in three dimensions for an incompressible fluid [3,4]: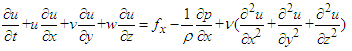 | (1.1) |
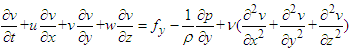 | (1.2) |
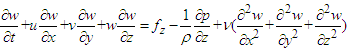 | (1.3) |
where u, v, and w are the velocity components in the x, y, and z directions, respectively; x, y, and z are the Cartesian coordinates; t is the time variable; fx, fy, and fz are the body force components in the x, y, and z directions, respectively; ρ is the density of the fluid, p is the pressure; and ν is the kinematic viscosity of the fluid. The term, including the kinematic viscosity on the right side of Eq. (1) is a feature of the equation that is usually attributed to the works of Navier [5] and Stokes [6]. The objective of teaching the NS equation, which is given by both the director committee of the university fundamental engineering course teaching of the Ministry of Education of China [7] and the author of the textbook employed in the course [8], is to understand the NS equation for the fluid mechanics course (B type), which indicates that the students should remember the equation first and then use the equation properly for the given problem.The relation between the study of the NS equation and undergraduate students in engineering and physics was introduced by Deissler in 1976 [9], who said, “Although a number of derivations of the Navier-Stokes equation can be found in works on fluid mechanics (e.g., Refs.1-7), the development still appears to be a stumbling block for most students. The derivation given here seems, at least to this writer, to be easier to grasp.” Drazin observed in 1987 [10], “Newton's second law for a system of particles is essentially a set of ordinary differential equations, but its generalisations for fluids, namely Euler's equations and the Navier-Stokes equations, are sets of partial differential equations. These are beyond what all school and most university pupils may be expected to learn,” and “The equations of fluid motion are difficult to solve, even for many simple problems even by use of a supercomputer. The difficulty is chiefly due to the nonlinearity of the partial differential equations of motion, but also to the geometrical complexity of most flows of interest.” Schneiderbauer and Krieger stated in 2014 [11], “Due to the fact that the Navier-Stokes equations are partial differential equations and their solutions are non-trivial, these are commonly not included in secondary school curriculums,” and therefore, they wrote an elaborate introduction on the NS equation to increase the interest and understanding by undergraduate students. The NS equation should be grasped, as mentioned previously, by the mechanical engineering undergraduate students in the course, although numerical solutions of the equation [10-14] have not been taught to the students. Checking the approach to studying the equation could be helpful in teaching fluid mechanics. The result could reflect certain study status of students.The semi-semester study of the NS equation is only recorded in 2021, and for checking the study-time effect, the original curriculum containing the midterm was also adopted in 2023, although the author knows that long-term study would be better for mastering the NS equation. The semi-semester study effect in 2023 and the related data on exercising the NS equation are reported in this paper.
2. Method
The inverse Stokes second problem was adopted to examine the effect of studying the NS equation, which has been described in detail in published works [1]; the procedure for solving the problem is also discussed [2]. The test for proportion was employed to evaluate the correctness of exercising the NS equation, and the statistical value Z [15] is given as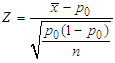 | (2) |
where p0 is the correctness, n is the number of students, and 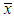 is the correct ratio obtained by dividing the number of students with correct answers by n. The significance level
is the correct ratio obtained by dividing the number of students with correct answers by n. The significance level 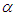 used for the evaluation was 0.05. The proportion test is a standard statistical method [15].The fluid mechanics course lasted for 12 weeks, with two class sessions each week. The midterm exam, which covered Volume 1 of Ding’s textbooks [4], was conducted in the first class in the seventh week of the course. The NS equation is usually taught in the fourth week; therefore, the students have three weeks to learn and understand the equation before the midterm. If there were only a final exam in the course, which occurred in the thirteenth week, the students would have ten weeks to learn. Moreover, the NS equation is used again in the study of both viscous incompressible internal flow and boundary layer flow in Volume 2 [4], which increases students’ opportunities to read and understand the equation. Therefore, verifying the study effect of the NS equation at the end of the course is beneficial for students. However, the disadvantage of having one examination at the end of the course is that it increases the amount of knowledge to be remembered, because textbooks are not allowed to be used in the exam.
used for the evaluation was 0.05. The proportion test is a standard statistical method [15].The fluid mechanics course lasted for 12 weeks, with two class sessions each week. The midterm exam, which covered Volume 1 of Ding’s textbooks [4], was conducted in the first class in the seventh week of the course. The NS equation is usually taught in the fourth week; therefore, the students have three weeks to learn and understand the equation before the midterm. If there were only a final exam in the course, which occurred in the thirteenth week, the students would have ten weeks to learn. Moreover, the NS equation is used again in the study of both viscous incompressible internal flow and boundary layer flow in Volume 2 [4], which increases students’ opportunities to read and understand the equation. Therefore, verifying the study effect of the NS equation at the end of the course is beneficial for students. However, the disadvantage of having one examination at the end of the course is that it increases the amount of knowledge to be remembered, because textbooks are not allowed to be used in the exam.
3. Results and Discussion
3.1. Correctness of the Solution
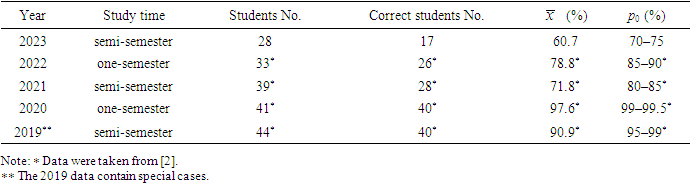
Table 1 shows the correctness statistics of exercising the NS equation during the semi-semester in 2023, along with the results from previous years. “Students No.” in Table 1 is the number of the students who took part in the exam, and “Correct students No.” is the number of students whose solutions were correct. As in previous studies [1,2], the correct solution means that the student lost less than five points out of a possible 20. The p0 (%) value, e.g. 70-75, indicate that the correctness was larger than 70%, but lower than 75%.Table 1. Study effect of the NS equation in two different periods
 |
| |
|
Three instances of semi-semester study are represented in Table 1, in which the correct ratios in both 2021 and 2023 were somewhat low, approximately 60-70%, and that in 2019 was high, at approximately 90%. One reason for the high correct ratio in 2019 was that students can see the NS equation given in the exam, as stated in [1,2]. Discarding the extra data in 2019, the correctness in 2021 and 2023 was lower than that in 2020 and 2022, which reaffirms the conclusion that a one-semester study on the NS equation is better than a semi-semester study [2]. A high accuracy of 99% in 2020 was also introduced in [1,2], which could be caused by four factors: some dishonest students, low error in calculation, superior study environment at home, and long-term study of the NS equation. The present study further supports the results of the long-term study.
3.2. NS Equation Error and Calculation Error
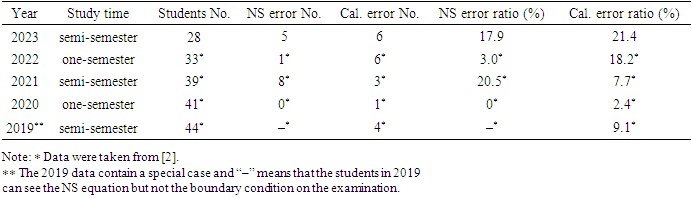
Table 2 shows the results of analyzing the errors in the solution of the problem for students with more than 5 points deducted; both NS equation errors and calculation errors are included in the analysis. The NS equation error includes two parts: the error of only the NS equation and the error of the boundary condition. “NS error No.” in Table 2 represents the number of students who could not correctly write the NS equation and the boundary condition. “Cal. error No.” is the number of students who could not correctly answer the question using differential calculus. “NS error ratio” equates to “NS error No.” divided by “Students No.,” and “Cal. error ratio” equates to “Cal. error No.” divided by “Students No.”Table 2. Error analysis of students with more than 5 points deducted
 |
| |
|
The error ratio of the NS equation for 2021 and 2023 in Table 2 is 20%, whereas that for 2020 and 2022 is approximately 3%. The difference between the semi-semester study in 2021 and 2023 and the one-semester study in 2020 and 2022 is apparent, and shows the positive effect of the one-semester study. The calculation error ratios in 2021 and 2023 in Table 2 are not significantly different from those in 2020 and 2022, indicating that the calculation capability of students does not seem to be related to the study time of the NS equation. The calculation capability of students in 2019-2021 seems superior to that in 2022-2023.
3.3. Separate NS Equation Error and Boundary Condition Error
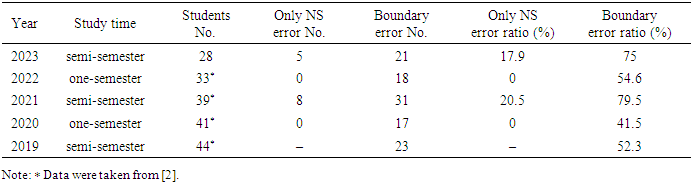
As mentioned in the solution procedure for the problem [2], there are three keys to the problem. The first is to write out the NS equation, the second is to calculate both the right and left terms of the NS equation using differential calculus, and the third is to write and check the boundary conditions. The errors caused by forgetting both the NS equation and boundary condition were analyzed as shown in Table 2. A detailed analysis of both the NS equation error and boundary condition error is further shown here, and the two errors are now separate.Table 3 shows the error results of NS equation error and boundary condition error separately for all the students in the five years from 2019 to 2023, in which “Only NS error No.” represents the number of students who could not write the NS equation correctly. “Boundary error No.” represents the number of students who could not write the boundary condition correctly. “Only NS error ratio” equates to “Only NS error No.” divided by “Students No.”, and “Boundary error ratio” equates to “Boundary error No.” divided by “Students No.”Table 3. Error analysis of NS equation and boundary condition errors for all students
 |
| |
|
An obvious phenomenon observed in Table 3 is that the error ratios of the NS equation in 2020 and 2022 were zero for students in one-semester study, and those in 2021 and 2023 were approximately 20% for students in semi-semester study. One-semester study is suitable for students who need more time to understand and remember the equations. Table 2 shows the NS equation error in 2022, as illustrated in Ref. [2]. The errors in this case were mainly caused by the boundary condition part of the problem. Therefore, there were no NS equation errors in 2022. The NS equation part of the “NS equation error” case in 2022 also contained some errors, e.g., the errors in the pressure term, which can be seen in the supplementary material in Ref. [2]. However, this type of slight error was not regarded as an error in the NS equation for beginners. If there was no correct viscous term in the NS equation written by the student, it was considered an error in the NS equation. The comparison between two-year semi-semester studies and two-year one-semester studies for the NS equation in Table 3 clearly shows the advantage of long-term study, although one examination in the course increases the amount of knowledge that students must remember.The error of the boundary condition problem in the five years is significant, as shown in Table 3, and approximately 50 percent or more of the students lost points on the boundary condition part of the problem. There are two boundary conditions of the problem: the wall velocity boundary on the oscillation infinite plate and the velocity boundary far away from the plate. The errors in the boundary condition of the problem were mainly caused by the latter boundary, and students can better understand the former because of the frequent occurrence of the wall velocity boundary in the examples in the textbook [4] used in the course. There was only one example of a velocity boundary far away from the plate [4] before the midterm, and many students were not familiar with such a boundary. This should be a difficult point of the problem. However, the points lost for this item were lower, approximately 2 points, and therefore, the boundary condition error was not reflected in the “NS error No.” data for students with more than 5 points deducted, as shown in Table 2.The error ratio of the boundary condition in Table 3 indicates a good effect of one-semester study on the boundary conditions; however, the data from 2019 contradict this conclusion. Semi-semester study could also not affect the study of the boundary conditions, and the reason for this is unknown.
4. Conclusions
Data on the study effect on the NS equation in 2023 were added to the present work, and the new data, along with the previous data, reaffirm that semi-semester study of the NS equation is not good for approximately 20% of students. One semester of study would be better for all students to remember the NS equation, which is a basic equation used in fluid mechanics. Further analysis of the separate NS equation and boundary condition problems indicates that approximately 50% or more of the students could lose points on the boundary conditions problem, mainly regarding the velocity boundary far from the plate for the inverse Stokes second problem, which is a difficult part of the problem.
ACKNOWLEDGEMENTS
The author thanks both Beijing Increscence Technology (BIT) Company Limited and the Chinese Society of Theoretical and Applied Mechanics (CSTAM) for providing English grammar services.ORCID iDsShuxin Huang, https://orcid.org/0000-0002-6878-664X
References
| [1] | Huang, S. (2022) Three exams of the Navier-Stokes equation. Am. J. Fluid Dyn. 12(2), 141–143. https://doi.org/10.5923/j.ajfd.20221202.02. |
| [2] | Huang, S. (2023) One-semester effect on the learning of the Navier-Stokes equation. Am. J. Fluid Dyn. 13(1), 1–3. https://doi.org/10.5923/j.ajfd.20231301.01. |
| [3] | Cengel, Y.A., Cimbala, J.M. (2018) Fluid Mechanics: Fundamentals and Applications, 4th edn. New York: McGraw-Hill Education. |
| [4] | Ding, Z. (2018) Fluid Mechanics, Vols. 1 and 2, 3rd edn. Beijing: Higher Education Press. (in Chinese) |
| [5] | Navier, C.L.M.H. (1821) Sur les Lois des mouvements des fluids, en ayant egard a l'adhesion des molecules. Ann Chimie 19, 244–260. (in French) |
| [6] | Stokes, G.G. (1845) On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids. Trans. Camb. Philos. Soc. 8, 287–319. |
| [7] | Director Committee of University Fundamental Engineering-Course Teaching of the Ministry of Education. (2019) Basic Requirements of Engineering-Course Teaching in Colleges and Universities. Beijing: Higher Education Press. (in Chinese) |
| [8] | http://www.icourses.cn/sCourse/course_2943.html. |
| [9] | Deissler, R.G. (1976) Derivation of the Navier–Stokes equations. Am. J. Phys. 44(11), 1128–1130. https://doi.org/10.1119/1.10205. |
| [10] | Drazin, P. (1987) Fluid mechanics. Phys. Educ. 22(6), 350–354. https://doi.org/10.1088/0031-9120/22/6/004. |
| [11] | Schneiderbauer, S., Krieger, M. (2014) What do the Navier-Stokes equations mean? Eur. J. Phys. 35(1), 015020. https://doi.org/10.1088/0143-0807/35/6/068003. |
| [12] | Fannon, J., Loiseau, J.C., Valluri, P., Bethune, I., Náraigh, L.O. (2016) High-performance computational fluid dynamics: a custom-code approach. Eur. J. Phys. 37(4), 045001. https://doi.org/10.1088/0143-0807/37/4/045001. |
| [13] | Pujante-Martínez, L., Clainche, S.L., Pérez, J.M., Ferrer, E. (2023) Learning fluid dynamics and the principles of flight: from primary school to STEM degrees. Eur. J. Phys. 44(4), 045002. https://doi.org/10.1088/1361-6404/acce0d. |
| [14] | McLean, D. (2018) Aerodynamic Lift, Part 1: The Science. Phys. Teach. 56(8), 516–520. https://doi.org/10.1119/1.5064558. |
| [15] | Barron, E.N., Del Greco, J.G. (2020) Probability and Statistics for STEM: A Course in One Semester. San Rafael: Morgan and Claypool Publishers. |



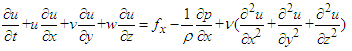
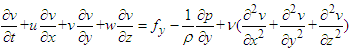
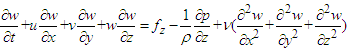
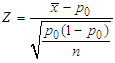
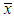 is the correct ratio obtained by dividing the number of students with correct answers by n. The significance level
is the correct ratio obtained by dividing the number of students with correct answers by n. The significance level 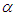 used for the evaluation was 0.05. The proportion test is a standard statistical method [15].The fluid mechanics course lasted for 12 weeks, with two class sessions each week. The midterm exam, which covered Volume 1 of Ding’s textbooks [4], was conducted in the first class in the seventh week of the course. The NS equation is usually taught in the fourth week; therefore, the students have three weeks to learn and understand the equation before the midterm. If there were only a final exam in the course, which occurred in the thirteenth week, the students would have ten weeks to learn. Moreover, the NS equation is used again in the study of both viscous incompressible internal flow and boundary layer flow in Volume 2 [4], which increases students’ opportunities to read and understand the equation. Therefore, verifying the study effect of the NS equation at the end of the course is beneficial for students. However, the disadvantage of having one examination at the end of the course is that it increases the amount of knowledge to be remembered, because textbooks are not allowed to be used in the exam.
used for the evaluation was 0.05. The proportion test is a standard statistical method [15].The fluid mechanics course lasted for 12 weeks, with two class sessions each week. The midterm exam, which covered Volume 1 of Ding’s textbooks [4], was conducted in the first class in the seventh week of the course. The NS equation is usually taught in the fourth week; therefore, the students have three weeks to learn and understand the equation before the midterm. If there were only a final exam in the course, which occurred in the thirteenth week, the students would have ten weeks to learn. Moreover, the NS equation is used again in the study of both viscous incompressible internal flow and boundary layer flow in Volume 2 [4], which increases students’ opportunities to read and understand the equation. Therefore, verifying the study effect of the NS equation at the end of the course is beneficial for students. However, the disadvantage of having one examination at the end of the course is that it increases the amount of knowledge to be remembered, because textbooks are not allowed to be used in the exam. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML

