American Journal of Fluid Dynamics

p-ISSN: 2168-4707    e-ISSN: 2168-4715

2023;  13(1): 1-3

doi:10.5923/j.ajfd.20231301.01

Received: Apr. 10, 2023; Accepted: Apr. 25, 2023; Published: Apr. 27, 2023

 

One-Semester Effect on the Learning of the Navier-Stokes Equation

Shuxin Huang1, 2

1Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai, China

2Key Laboratory of Hydrodynamics of the Ministry of Education, Shanghai Jiao Tong University, Shanghai, China

Correspondence to: Shuxin Huang, Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai, China.

Email:

Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.

This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract

The effect of studying the Navier-Stokes (NS) equation of undergraduate student is examined again in this work based on the exams in the recent four years from 2019 to 2022. Proportion test method is adopted in the research. A result shows that the students can remember the equation much better via one semester study than that via semi-semester study, which seems normal but conflicts the teaching plan of the fluid mechanics course including a midterm.

Keywords: NS equation, Study effect, Fluid mechanics, Inverse of the Stokes second problem, Hypothesis test, Exam, Undergraduate student, One semester study

Cite this paper: Shuxin Huang, One-Semester Effect on the Learning of the Navier-Stokes Equation, American Journal of Fluid Dynamics, Vol. 13 No. 1, 2023, pp. 1-3. doi: 10.5923/j.ajfd.20231301.01.

Article Outline

1. Introduction
2. Method
3. Results and Discussion
4. Conclusions
Supplemental
ORCID iDs

1. Introduction

Two recent works [1,2] on the research of the study effect of the Navier-Stokes (NS) equation [3-7] indicate three conclusions. The first is that the inverse Stokes problem [5], i.e., the velocity of the second Stokes problem [6,8-10] is given and the question is to check the validity of the velocity for the NS equation and boundary conditions, is more suitable for student to study the NS equation. The second is that more than 80% students can use the NS equation properly at the end of the engineering fluid mechanics course of Huang [2], and the last is that web-home mode could have some merit for the learning of fluid mechanics.
The experimental data that support the web-home mode of study was obtained in the spring of 2020, because there was an epidemic of COVID-19 in China and students studied at home via web teaching in the year. The high correctness of solving the inverse Stokes problem in 2020 [2] is attributed to four possible factors, i.e., some dishonest students, low error in calculation, superior study environment at home, and long-term study of the NS equation. It is difficult to check these factors formed in the special 2020.
However, there occurred COVID-19 in Shanghai Jiao Tong University and in Shanghai in the spring of 2022, and we had to study and teach through web again. At the end of the course, the inverse Stokes problem was still employed to examine the study effect of the NS equation. The results are diversity accompanied by definite conclusion on the work, especially on the time used to study the equation.

2. Method

The inverse Stokes problem can be found in the references [2,5]. The solution of the problem includes about three steps: (1) write out the NS equation; (2) calculate both the right and the left term of the equation using the given velocity and differential calculus, and then check if the right equates the left; (3) examine the boundary conditions using the given velocity.
A statistic value Z [11] was employed to evaluate the correctness of exercising the NS equation,
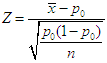(1)
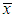where p0 is the correctness, is the correct ratio, n is the number of students. 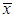is obtained by dividing the number of the students with correct answer by n. The significant level used for p0 is α = 0.05, which is also the same as that in [1,2]. Test for proportion is a standard statistical method.

3. Results and Discussion

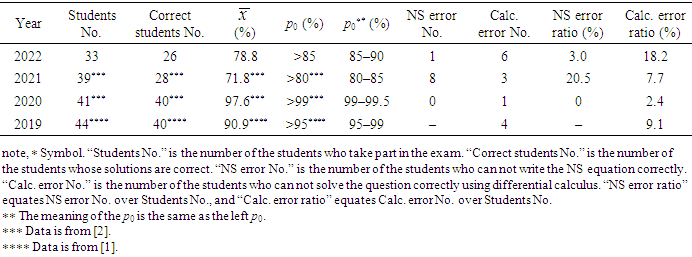
Table 1 shows the examination on the study effect of the NS equation, where the data in 2022 is new and part of the data in the previous three years is new. There are two identical symbols p0 in Table 1, where the right can clearly indicate the range of the maximum correctness of solving the problem. For example, the maximum correctness in 2022 should be in the range of 85%–90%, which means that the maximum correctness is larger than 85% but lower than 90%. Moreover, there are two blanks in 2019, because students can see the NS equation in the exam and they were not required to remember the equation. In addition, solving the question correctly means that student only loses less than 5 score in the summation score of 20 of the question [1,2].
Table 1. Study effect of the NS equation checked by validating velocity*
     
The correctness in 2022 is higher than 85% in Table 1, which is slightly higher than 80% in 2021 but evidently lower than 99% in 2020. The examination situations are different in three years. In 2022 and 2020, students studied one semester, and in 2021, students only studied half of a semester. Therefore, the low correctness in 2022 contains problem. To evaluate the study effect of the NS equation, the error was divided into two cases. One is that the error is caused by not remembering the NS equation, and the other is caused by not calculating the value of the equation correctly using differential calculus. Because differential calculus is not used in checking boundary condition, the error of boundary condition is regarded as the error of NS equation. The corresponding data of the errors have been listed in Table 1.
We can see clearly in Table 1 that calculation error is more significant than forgetting NS equation in 2022, which indicates that students can remember the NS equation through one-semester study of fluid mechanics. This is a normal phenomenon that one-semester study in 2022 should be better than semi-semester study in 2021. Some students can not remember the NS equation due to semi-semester study in 2021. One-semester study of fluid mechanics should be a better mode for mastering the NS equation, which are supported by the data in 2021 and 2022. Although the data in 2020 also supports that one-semester study is good, and as said in the introduction section, there are four factors mixed together influencing the conclusion.
The solution of a student on the exercise, which is regarded as an error of NS equation in 2022, was provided in the supplementary material, and we can see that the error of the NS equation is slight, which is not regarded as the case losing score. The student lost 6 score, in which 2 is for calculation and 4 for NS equation. The lost 4 score is actually for boundary conditions. As said above, the error of boundary condition is regarded as the error of NS equation. This affirms again that students can remember the NS equation via one-semester study.
The calculation error in 2022 is somewhat high, although there are calculation errors in 2019 and 2021. In 2019, the NS equation was given in the exam and students still had calculation errors. Thus, the calculation errors in 2019, 2021 and 2022 seem not related to the study effect of the NS equation from the course. The reason for the high calculation error in 2022 is not clear. The author of the work may also have deviation in marking. The low calculation error in 2020 could be due to the effect of the web-home mode, and the mood of the students under the circumstance of exam could be more stable at home. A recent point of view [12] indicates that inclusive learning environments (including perceived recognition, perceived effectiveness of peer interaction, and sense of belonging) can improve student learning, and therefore, web-home mode should be a natural good environment if student cares about study or has some motivational beliefs of the course.
The engineering fluid mechanics course [5,13] that I conduct contains nine chapters: introduction, fluid properties, kinematics, differential-type equation for fluid flow, integral-type equation for fluid flow, dimensional analysis and similarity, fluid statics, plane potential flow, viscous flow in ducts, and boundary layer theory. There are two exams in a semester for the purpose of alleviating the exam content in one exam as well as promoting the study of fluid mechanics. The first five chapters are usually checked in midterm and the others in terminal. Therefore, the NS equation is in midterm. There is only a terminal exam in the special 2020 and 2022, which forms the particular examination of the study-time effect. Long-term study is better for students to master the NS equation in the course.
The difference between the 2020’s and 2022’s exam is at study environment. Both the study and exam in 2020 were at home, and that in 2022 at school. The influence of the difference is small on remembering the NS equation. However, it is unclear whether environment influences calculation for some students. If school mode affects calculation, the students have to improve the corresponding capability to alleviate error.

4. Conclusions

The experience of examining the study effect of the NS equation of the author in 2022 affirms a conclusion that long-term study is beneficial to master the NS equation in the engineering fluid mechanics course. The result has conflict with the normal teaching plan, and canceling midterm could be an alternative teaching method for the course. The slightly high calculation error in 2022’s exam is a new phenomenon. The merit of the web-home mode in 2020 for study is still apparent in comparison with that of the web-school mode in 2022 for some students, which appears that the calculation capability of the students in 2020 seems superior to that in 2022.

Supplemental

Supplemental material associated with this article can be found in the online version, at http://article.sapub.org/10.5923.j.ajfd.20231301.01.supplementa.pdf.

ORCID iDs

Shuxin Huang, https://orcid.org/0000-0002-6878-664X.

References

[1]  Huang, S. (2020) Two pieces of homework. 2019 Symposium of reformation and innovation of mechanics teaching in university. Beijing: Higher Education Press. https://2d.hep.com.cn/1260391/8 (In Chinese).
[2]  Huang, S. (2022) Three exams of the Navier-Stokes equation. Am. J. Fluid Dyn. 12(2), 141–143. https://doi.org/10.5923/j.ajfd.20221202.02.
[3]  Deissler, R.G. (1976) Derivation of the Navier–Stokes equations. Am. J. Phys. 44, 1128–1130. https://doi.org/10.1119/1.10205.
[4]  Drazin, P. (1987) Fluid mechanics. Phys. Educ. 22, 350–354. https://doi.org/10.1088/0031-9120/22/6/004.
[5]  Ding, Z. (2003) Fluid Mechanics Vol. 2. Beijing: Higher Education Press. p. 92, 108-109. (In Chinese).
[6]  Kundu, P.K., Cohen, I.M., Dowling, D.R. (2012) Fluid Mechanics, 5th edn. Amsterdam: Elsevier. p. 115, 337.
[7]  Schneiderbauer, S., Krieger, M. (2014) What do the Navier–Stokes equations mean? Eur. J. Phys. 35, 015020. https://doi.org/10.1088/0143-0807/35/6/068003.
[8]  Stokes, G.G. (1851) On the effect of internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 9, 8.
[9]  Rayleigh, L. (1911) On the motion of solid bodies through viscous liquids. Phil. Mag. 21, 697–711.
[10]  Schlichting, H., Gersten, K. (2017) Boundary Layer Theory, 9th edn. Berlin: Springer. p. 129.
[11]  Barron, E.N., Del Greco, J.G. (2020) Probability and Statistics for STEM: A Course in One Semester. San Rafael: Morgan & Claypool Publishers. p. 115-116.
[12]  Li, Y., Singh, C. (2022) Inclusive learning environments can improve student learning and motivational beliefs. Phys. Rev. Phys. Educ. Res. 18, 020147. https://doi.org/10.1103/PhysRevPhysEducRes.18.020147.
[13]  http://www.icourses.cn/sCourse/course_2943.html.