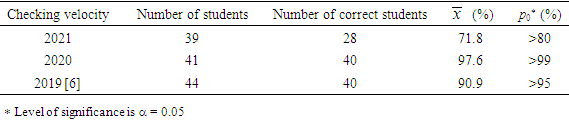American Journal of Fluid Dynamics

p-ISSN: 2168-4707    e-ISSN: 2168-4715

2022;  12(2): 141-143

doi:10.5923/j.ajfd.20221202.02

Received: Oct. 31, 2022; Accepted: Nov. 12, 2022; Published: Nov. 24, 2022

 

Three Exams of the Navier-Stokes Equation

Shuxin Huang1, 2

1Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai, China

2Key Laboratory of Hydrodynamics of the Ministry of Education, Shanghai Jiao Tong University, Shanghai, China

Correspondence to: Shuxin Huang, Department of Engineering Mechanics, Shanghai Jiao Tong University, Shanghai, China.

Email:

Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.

This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract

By comparing and analyzing the exam scores of exercising the Navier-Stokes (NS) equation in 2019, 2020 and 2021, the effect of studying the NS equation for undergraduate student is studied in the present work. The results show that at least more than 80% students can remember and use the NS equation properly. Moreover, the high correctness in 2020 is also analyzed, in which the ‘web-home’ mode for study is a feature and could have some merit.

Keywords: NS equation, Study effect, Fluid mechanics, Inverse of the Stokes second problem, Hypothesis test, Exam, Undergraduate student

Cite this paper: Shuxin Huang, Three Exams of the Navier-Stokes Equation, American Journal of Fluid Dynamics, Vol. 12 No. 2, 2022, pp. 141-143. doi: 10.5923/j.ajfd.20221202.02.

Article Outline

1. Introduction
2. Methods
    2.1. Hypothesis Test Method
    2.2. Inverse of the Stokes Second Problem
3. Results and Discussion
4. Conclusions
Supplemental

1. Introduction

The Navier-Stokes (NS) equation [1,2] is a fundamental theoretical model in fluid mechanics, which is taught in my course of engineering fluid mechanics. The NS equation is a differential type mathematical model, and there is some difficulty to master the equation for undergraduate student [3-5] who begins to study the equation. The study effect on the equation has been reported in another work of Huang [6] in 2020, where two questions were employed to examine the study effect. One question is to solve the Stokes second problem [7-10], and the other is to solve the inverse problem of the Stokes problem [11], i.e., the velocity of the second Stokes problem is given and the question is to check whether the velocity meets both the NS equation and boundary conditions. The results in the examination [6] indicate that the later is more effective for student to study the NS equation and to do exercise on the equation.
The study effect on the NS equation is checked again in the present work, which includes the recent results in both 2020 and 2021. The question used is to examine the validity of the velocity of the second Stokes problem, and further results of studying the NS equation of student are shown here.

2. Methods

2.1. Hypothesis Test Method

To evaluate the effect of studying the NS equation of student, a statistic value Z [12] was used to express the correctness of doing the exercise, which is defined as follows,
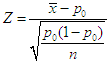(1)
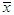where p0 is the correctness, is the correct ratio, n is the number of students. 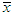is obtained using the number of the students with correct answer over n. The significant level α = 0.05 is set to evaluate the correctness.

2.2. Inverse of the Stokes Second Problem

The question of checking the validity of the velocity of the second Stokes problem [11] is,
Suppose that incompressible constant-viscosity fluid lies at rest in the region of 0 < y < ∞, and suppose that a infinite flat plate at y=0 executes cosine motion in the x-direction according to the velocity u=Ucos(ωt), in which U and ω are constant velocity and angle frequency respectively, and t is a variable time. Do not consider gravity and pressure. Check whether the following velocities of the fluid in the flow field meet the NS equation and boundary condition,
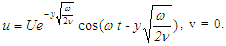(2)

3. Results and Discussion

In both the terminal examination of 2020 and the midterm of 2021, the students solved the question, and the results are listed in Table 1. The correct ratio is 97.6% in 2020, which is calculated using 40 over 41 and then multiplying 100. The ratio is very high, and the correctness is higher than 99% according to the test of hypothesis for binomial distribution [12], which is under the level of significance of 0.05. Therefore, the study effect of the NS equation is quite good. The meaning of solving the question correctly [6] is that the score is 20 for the question and if the student only loses less than 5 score, who is regarded as correctly using the NS equation. Detailed lost scores of exercising the NS equation for the students in 2019, 2020, and 2021 are shown in supplemental material.
Table 1. Study effect of the NS equation
     
The correct ratio in 2021 is 71.8% in Table 1, and the corresponding correctness is higher than 80%, which is evidently lower than the correctness in 2020. Moreover, Table 1 also shows the result in 2019 [6], and the correctness is higher than 95%, which approaches the correctness in 2020.
There are differences between the processes of three examinations and the corresponding studies. The first is that the NS equation was given in the exam in 2019, and not given in both 2020 and 2021. Thus, the students in the later two years should remember the equation and then solve the question. The second is that the question was solved in mid-term in both 2019 and 2021, and solved in terminal exam in 2020. Therefore, long-term study on the NS equation exists for the students in 2020. The last is that the question was solved in classroom without any related material, such as textbook, left for the students to refer to in both 2019 and 2021, and solved at home in 2020 though the students were told not to see any related material and supervised through webcam.
According to the status of both exams and studies, the differences between three exams are discussed below. (1) The high correctness in 2019 should be related to the fact that the students can see the NS equation directly. What they did is to put the velocity into the NS equation to check whether the left of the NS equation is equal to the right, and the possible error should be at the calculation of derivative. (2) The drop of correctness in 2021 could be due to the fact that some students can not remember the NS equation as well as make errors in calculation. (3) The case in 2020 is complicated. The first is that the high correctness indicates that the students can remember the equation, but in comparison with the result of 2021, there could be a guess whether there are some dishonest students because supervision is via webcam. The second is that high correctness indicates a low error in calculation. The third is that study effect could be better at home in 2020, for example, the influence of environment could be less and student could spend more time studying. There was an epidemic of COVID-19 in 2020, and student studied at home via web teaching. The last is that long-term study of the NS equation in 2020 could be a factor to help student master the equation better, because the exam in 2020 was at the end of the course and those in both 2019 and 2021 was at midterm. The first discussion on the 2020 case is negative but the later three are positive.
In the book of director committee of university fundamental engineering-course teaching of the Ministry of Education in China [13], the objective of teaching is to understand the NS equation for fluid mechanics course (B type), which is same as that in the outline of the engineering fluid mechanics course [14] that I conduct. The recent 3-year practices show that more than 80 percent students can use the NS equation to solve the designed problem at the end of the course. Moreover, the result in 2019 indicates a better effect of studying and applying the equation if the students can see the equation.

4. Conclusions

The study effect of the NS equation in the recent three years was evaluated in this study. The results indicate that over 80% of the students can remember the NS equation and use the equation properly to solve the designed problem at the end of the course. The practice in 2020 shows that the ‘web-home’ mode for study could have some merit by comparison with that in classroom.

Supplemental

Figure S1. Lost scores of the exercise of the NS equation for the students in (1) 2019, (2) 2020, and (3) 2021, respectively

References

[1]  Navier, P.M. (1821) Sur les Lois des mouvements des fluids, en ayant egard a l'adhesion des molecules. Ann Chimie 19, 244–260. (In French)
[2]  Stokes, G.G. (1845) On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids. Trans. Camb. Phil. Soc. 8, 287–319.
[3]  Deissler, R.G. (1976) Derivation of the Navier–Stokes equations. Am. J. Phys. 44, 1128–1130. https://doi.org/10.1119/1.10205.
[4]  Drazin, P. (1987) Fluid mechanics. Phys. Educ. 22, 350–354. https://doi.org/10.1088/0031-9120/22/6/004.
[5]  Schneiderbauer, S., Krieger, M. (2014) What do the Navier–Stokes equations mean? Eur. J. Phys. 35, 015020. https://doi.org/10.1088/0143-0807/35/6/068003.
[6]  Huang, S. (2020) Two pieces of homework. 2019 Symposium of reformation and innovation of mechanics teaching at university. Beijing: Higher Education Press. https://2d.hep.com.cn/1260391/8. (In Chinese)
[7]  Stokes, G.G. (1851) On the effect of internal friction of fluids on the motion of pendulums Trans. Camb. Phil. Soc. 9, 8.
[8]  Rayleigh, L. (1911) On the motion of solid bodies through viscous liquids. Phil. Mag. 21, 697–711.
[9]  Kundu, P.K., Cohen, I.M., Dowling, D.R. (2012) Fluid Mechanics, 5th edn. Amsterdam: Elsevier. pp. 337.
[10]  Schlichting, H., Gersten, K. (2017) Boundary Layer Theory, 9th edn. Berlin: Springer. pp. 129.
[11]  Ding, Z. (2003) Fluid Mechanics Vol. 2. Beijing: Higher Education Press. pp. 108. (In Chinese)
[12]  Barron, E.N., Del Greco, J.G. (2020) Probability and Statistics for STEM: A Course in One Semester. San Rafael: Morgan & Claypool Publishers. pp. 115.
[13]  Director committee of university fundamental engineering-course teaching of the Ministry of Education. (2019) Basic requirements of engineering-course teaching in colleges and universities. Beijing: Higher Education Press. pp. 31. (In Chinese)
[14]  http://www.icourses.cn/sCourse/course_2943.html.